MQL5中的替代风险回报标准

MetaTrader 5 — 示例 | 22 三月 2024, 10:09

355

Francis Dube

概述

所有交易员都希望尽可能最大限度地提高投资回报率，但更高的回报率通常会带来更高的风险。这就是为什么风险调整后的回报是衡量投资行业业绩的主要指标的原因。风险调整收益有许多不同的衡量标准，每一种都有自己的优点和缺点。夏普比率是一种流行的风险收益衡量标准，以对所分析的收益分配强加不切实际的先决条件而闻名。这不可避免地导致了替代性能指标的发展，这些指标试图提供夏普比率的同样普遍性，而不存在其不足之处。在本文中，我们提供了替代风险回报指标的实现，并生成假设的权益曲线来分析其特征。

模拟权益曲线

为了确保可解释性，我们将使用标普500指数数据作为模拟交易策略的基础。我们不会使用任何特定的交易规则，而是使用随机数来生成权益曲线和相应的收益序列。初始资本将标准化为可配置的金额。随机数将由一个种子定义，这样任何想复制实验的人都可以这样做。

可视化权益曲线

下图显示了一个Metatrader 5（MT5）应用程序，该应用程序被实现为专家顾问（EA 交易），显示了三条权益曲线。红色权益曲线是衍生蓝色和绿色权益曲线的基准。可以通过配置初始资本来更改基准。可根据应用进行调整。

模拟权益曲线EA

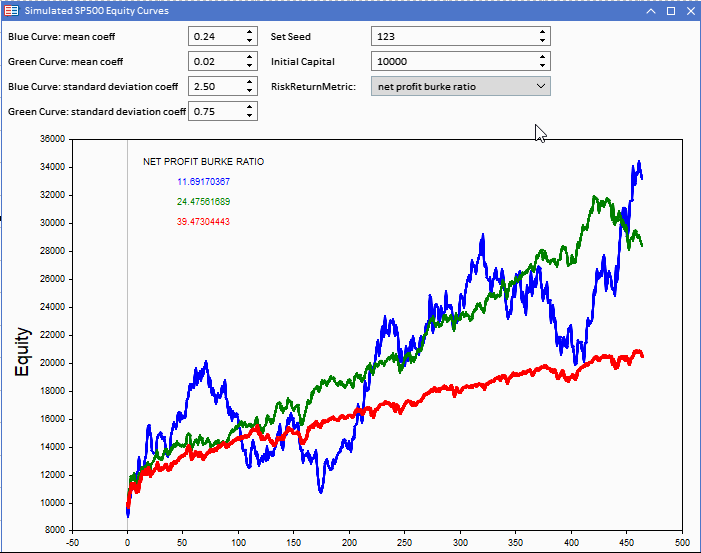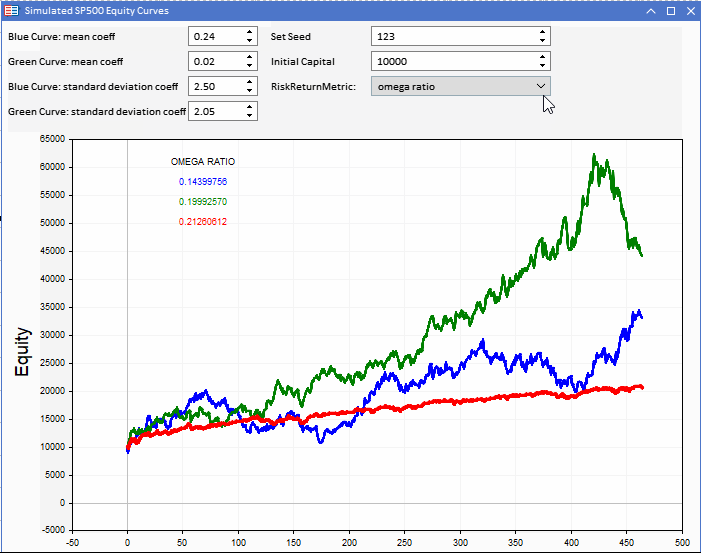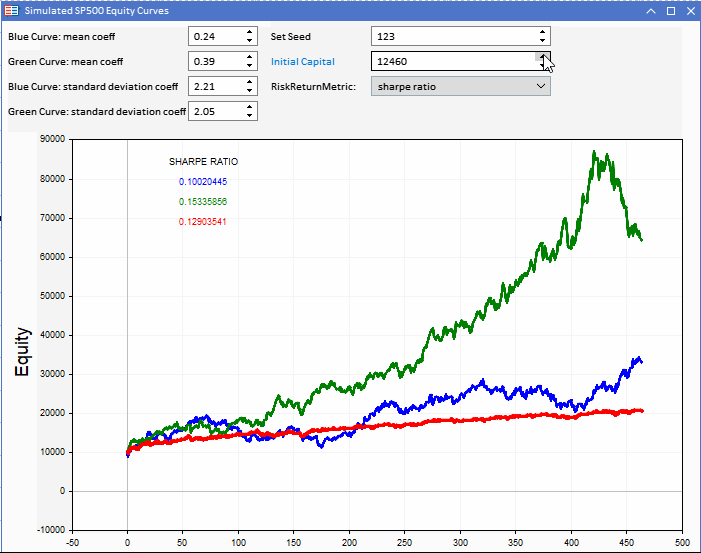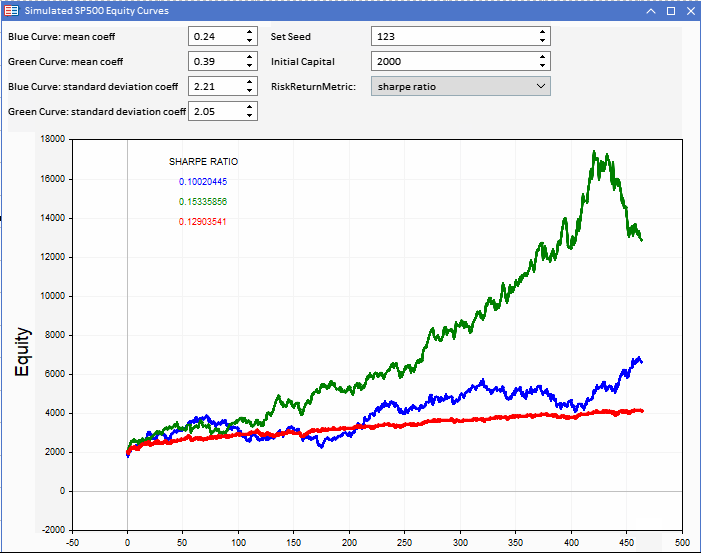
权益曲线将基于基准系列创建。每一个都由一个随机分量定义，该分量可以通过两个可调常数进行控制，平均系数和标准偏差系数。这些与基准收益的标准差相结合，确定了用于生成两条假设权益曲线的正态分布随机数的参数。

所选期间

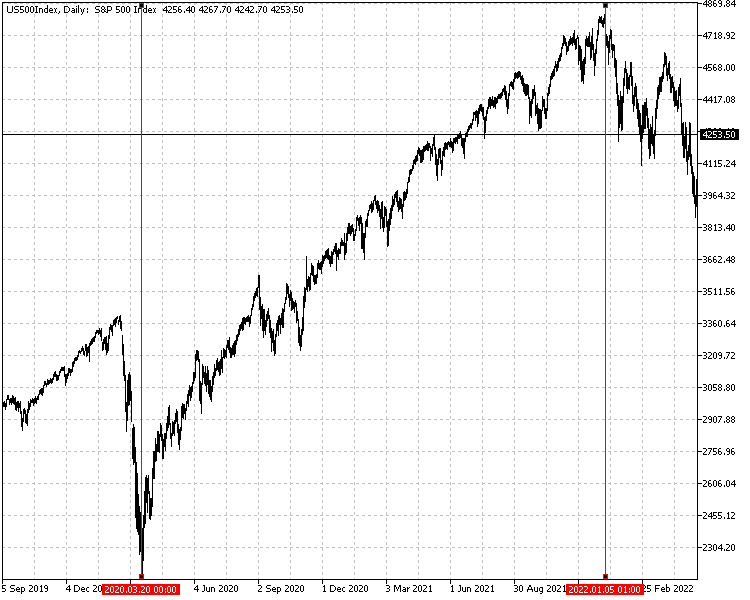
我们首先使用2020年3月20日至2022年1月5日（含）期间的标普500指数收盘价计算收益。权益曲线是由一系列收益建立起来的。通过定义权益和回报的系列，我们将比较与给定权益曲线外观一起计算的绩效结果

该应用程序的代码附在文章后面

回撤比率

回撤代表一种策略在任何两个时间点之间损失的最大净值。这个值表明了一项策略为实现其收益而承担的风险（如果有的话）。当统计和汇总由任意数量的最高回撤组成的序列时，结果可以用作可变性的衡量标准。

Burke比率

1994年，Burke写了一篇题为“更锋利的夏普比率”的论文，介绍了Burke比率作为人们熟悉的夏普比率的替代品。Burke比率用Sharpe比率公式中的分母代替指定数量的最高绝对回撤的平方和。分子可以是策略/投资组合的平均回报率或绝对货币回报率，即净利润。我们将看看这两种版本的计算。我们将这两个版本区分为基于净利润的Burke比率和平均收益Burke比率。公式如下。

基于净利润的Burke比率公式

基于平均收益的Burke比率公式

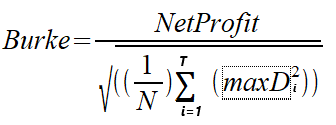
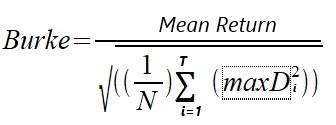
MaxD是根据净值计算的最大T绝对回撤的系列。N表示计算中使用的净值的数量

净利润 Burke 比率实现为netprofit_Burke（）函数。该函数需要一组描述净值曲线的净值数值，以及一个表示计算中要考虑的最高回撤次数的整数值。

//+------------------------------------------------------------------+
//|Net profit based Burke ratio                                      |
//+------------------------------------------------------------------+
double netprofit_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
        {
         sumdd+=(outdd[i]*outdd[i]);
        }
      return (in_ec[insize-1]-in_ec[0])/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

当指定默认值为零时，函数使用公式N/20设置要考虑的回撤次数，其中N是权益数组的大小。

为了收集指定数量的回撤，将调用MaxNDradowns（）函数。它输出一系列按升序排列的最高绝对回撤。

//+------------------------------------------------------------------+
//|Maximum drawdowns function given equity curve                     |
//+------------------------------------------------------------------+
bool MaxNDrawdowns(const int num_drawdowns,double &in_ec[],double &out_dd[])
  {
   ZeroMemory(out_dd);

   ResetLastError();

   if(num_drawdowns<=0)
     {
      Print("Invalid function parameter for num_drawdowns ");
      return false;
     }
   double u[],v[];

   int size = ArraySize(in_ec);

   if((ArrayResize(v,(size*(size-1))/2)< int((size*(size-1))/2))||
      (ArraySize(out_dd)!=num_drawdowns && ArrayResize(out_dd,num_drawdowns)<num_drawdowns))
     {
      Print(__FUNCTION__, " resize error ", GetLastError());
      return false;
     }

   int k=0;
   for(int i=0; i<size-1; i++)
     {
      for(int j=i+1; j<size; j++)
        {
         v[k]=in_ec[i]-in_ec[j];
         k++;
        }
     }

   ArraySort(v);

   for(int i=0; i<k; i++)
     {
      if(v[i]>0)
        {
         if(i)
           {
            if(!ArrayRemove(v,0,i))
              {
               Print(__FUNCTION__, " error , ArrayRemove: ",GetLastError());
               return false;
              }
            else
               break;
           }
         else
            break;
        }
     }

   size=ArraySize(v);

   if(size && size<=num_drawdowns)
     {
      if(ArrayCopy(out_dd,v)<size)
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      else
         return (true);
     }


   if(ArrayCopy(out_dd,v,0,size-num_drawdowns,num_drawdowns)<num_drawdowns)
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return false;
     }


   return(true);

  }

使用平均收益作为分子的Burke比率计算被实现为 meanreturns_Burke 函数，并且具有类似的输入参数。

//+------------------------------------------------------------------+
//|Mean return based Burke ratio                                     |
//+------------------------------------------------------------------+
double meanreturns_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double rets[];

   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(ArrayResize(rets,insize-1)<insize-1)
     {
      Print(__FUNCTION__," Memory allocation error ",GetLastError());
      return 0;
     }

   for(int i=1; i<insize; i++)
      rets[i-1] = (in_ec[i]/in_ec[i-1]) - 1.0;

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
         sumdd+=(outdd[i]*outdd[i]);
      return MathMean(rets)/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

净利润与最大回撤率

以净利润为分子的Burke比率公式类似于净利润与最大回撤的比率（Netprofit to Maximum Drawdown ratio，NPMD）。不同之处在于在NPMD比率的计算中使用了单个最高回撤。

NPMD 比率公式

NPMD计算被实现为netProfiMaxDD（）函数，需要净值数组作为输入。

//+------------------------------------------------------------------+
//|Net profit to maximum drawdown ratio                              |
//+------------------------------------------------------------------+
double netProfiMaxDD(double &in_ec[])
  {
   double outdd[];
   int insize=ArraySize(in_ec);

   if(MaxNDrawdowns(1,in_ec,outdd))
      return ((in_ec[insize-1]-in_ec[0])/outdd[0]);
   else
      return 0;
  }

引入基于回撤的比率是为了解决对夏普比率的一些批评。计算不会惩罚异常或大的增益，并且最重要的是没有参数。尽管有利，但分母中使用绝对提款使Burke和NPMD比率都倾向于具有相对温和的下行峰值的策略。

Burk 比率结果

参考权益曲线可视化工具。蓝色曲线的回报率最高，但得分低于其他曲线。

基于平均收益的Burke比率结果

这两个比率的基准值都强调了在用于比较策略性能时，这些指标的误导性。尽管其他曲线提供了更多的实际回报，但基准比率明显更高。

NPMD比率结果

相对于使用夏普比率的负回报分布，使用绝对回撤可能会过度强调风险。

夏普比率结果

比较夏普分数，我们发现绿色曲线最高，模拟策略结果之间的差异要小得多。

回撤比率解释

Burke或NPMD比率越高，投资策略的风险调整绩效越好。这意味着与所承担的风险相比，该策略产生了更高的回报。

- 如果Burke或NPMD比率大于0，则表明与计算的风险相比，投资策略提供了超额回报

- 如果Burke或NPMD比率小于0，则表明与所承担的风险相比，投资策略没有产生足够的超额回报。

偏矩比

基于偏矩的比率是夏普比率的另一种替代方案。它们基于半方差的统计概念，并提供了对策略在下行风险（负回报）与上行潜力（正回报）方面表现如何的见解。为了计算偏矩比，我们首先需要确定部分利润和部分亏损。这些值是通过确定阈值回报水平得出的，通常是最小可接受回报率或无风险率，并计算每次观测的实际回报率和阈值回报率之间的差。

该计算可以忽略高于较低偏矩的阈值或低于较高偏矩（higher partial moment，HPM）的阈值的差异。较低偏矩（lower partial moment，LPM）测量低于阈值的收益的平方偏差，而较高偏矩测量超过阈值的收益平方偏差。偏矩通过关注低于或高于特定阈值的回报相关的风险，提供了与回撤率相比的风险的另一种视角

以下分别是LPM和HPM的公式：

LPM 公式

HPM 公式

其中thresh是阈值，x是观察到的返回值，max确定所得差值与零之间的最大值，然后再提高到n的幂。n定义了偏矩的程度。当n＝0时，LPM变为观测值小于阈值的概率，而HPM给出其高于阈值的概率。N是观察到的收益次数。我们将研究的两个偏矩比是广义Omega和上行潜能比率（Upside Potential Ratio，UPR）。

Omega

广义Omega由单个n次项和定义计算中使用的LPM的阈值定义。

Omega 公式

omega（）函数通过将一个返回数组作为输入来实现 Omega 比率的计算。该函数使用2阶较低的偏矩，回报值阈值为零。

//+------------------------------------------------------------------+
//|omega ratio                                                       |
//+------------------------------------------------------------------+
double omega(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);

   if(pmomentl)
      return MathMean(rt)/pmomentl;
   else
      return 0;
  }

上行潜能比率

UPR使用两个n阶项（公式中的n1和n2）和阈值。n1确定分子中的HPM程度，n2指定分母的LPM程度。

UPR 公式

与Omega性能度量的实现类似，upsidePotentialRatio（）函数计算UPR比率。该计算还使用2阶偏矩和定义为零的回报阈值。

//+------------------------------------------------------------------+
//|Upside potential ratio                                            |
//+------------------------------------------------------------------+
double upsidePotentialRatio(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentu=MathPow(partialmoment(2,rt,rb,true),0.5);
   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);
   if(pmomentl)
      return pmomentu/pmomentl;
   else
      return 0;
  }

偏矩计算是在 partialmoment（）函数中实现的。它需要一个无符号整数、两个 double 类型和布尔值的数组的阶数作为输入。第一个数组应包含观察到的回报，第二个数组应包括计算中使用的阈值或基准回报。布尔值确定要计算的偏矩的类型，对于较高的偏矩为true，对于较低的偏矩则为false。

//+------------------------------------------------------------------+
//|Partial Moments                                                   |
//+------------------------------------------------------------------+
double partialmoment(const uint n,double &rt[],double &rtb[],bool upper=false)
  {
   double pm[];
   int insize=ArraySize(rt);

   if(n)
     {
      if(ArrayResize(pm,insize)<insize)
        {
         Print(__FUNCTION__," resize error ", GetLastError());
         return 0;
        }

      for(int i=0; i<insize; i++)
         pm[i] = (!upper)?MathPow(MathMax(rtb[i]-rt[i],0),n):MathPow(MathMax(rt[i]-rtb[i],0),n);
      return MathMean(pm);
     }
   else
     {
      int k=0;
      for(int i=0; i<insize; i++)
        {
         if((!upper && rtb[i]>=rt[i]) || (upper && rt[i]>rtb[i]))
           {
            ArrayResize(pm,k+1,1);
            pm[k]=rt[i];
            ++k;
           }
         else
            continue;
        }

      return MathMean(pm);

     }

  }

UPR 结果

查看我们的净值曲线的Omega和UPR比率，我们注意到评级与夏普比率相似。

Omega 结果

与波动较大的净值曲线相比，一致性再次受到青睐。Omega 看起来特别像是夏普比率的可行替代品。

偏矩比解释

相对于UPR，Omega的解释要直截了当得多。omega 越高越好。负值表示赔钱策略，正值表示相对于风险承担提供超额回报的业绩。

另一方面，当涉及到解释时，UPR可能有点奇怪，看看一些具有不同业绩曲线的模拟净值曲线。

奇怪的UPR结果

蓝色净值曲线显示出负回报，但UPR的结果是正的。更奇怪的是绿色和红色净值曲线的结果。曲线本身几乎与绿色权益曲线相似，产生了更好的回报，但UPR值小于红色曲线。

收益的回归分析——Jensen的Alpha

线性回归可以构建最适合数据集的直线。因此，基于回归的指标衡量权益曲线的线性。Jensen的Alpha计算标准回归方程中Alpha的值。它量化了基准收益和观察到的收益之间的关系。

Jensen 的 Alpha 公式

为了计算alpha的值，我们可以使用最小二乘拟合方法。函数leastsquarefit（）将定义响应和预测器的两个数组作为输入。在这种情况下，响应将是观察到的回报的数组，预测因子是基准回报的数组。函数输出alpha和beta值，调用函数时应提供它们的引用。

//+------------------------------------------------------------------+
//|linear model using least squares fit y=a+bx                       |
//+------------------------------------------------------------------+
double leastsquaresfit(double &y[],double &x[], double &alpha,double &beta)
  {
   double esquared=0;

   int ysize=ArraySize(y);
   int xsize=ArraySize(x);

   double sumx=0,sumy=0,sumx2=0,sumxy=0;

   int insize=MathMin(ysize,xsize);

   for(int i=0; i<insize; i++)
     {
      sumx+=x[i];
      sumx2+=x[i]*x[i];
      sumy+=y[i];
      sumxy+=x[i]*y[i];
     }

   beta=((insize*sumxy)-(sumx*sumy))/((insize*sumx2)-(sumx*sumx));
   alpha=(sumy-(beta*sumx))/insize;

   double pred,error;

   for(int i=0; i<insize; i++)
     {
      pred=alpha+(beta*x[i]);
      error=pred-y[i];
      esquared+=(error*error);
     }

   return esquared;

  }

将Jensen的Alpha应用于我们模拟的权益曲线，我们得到了绿色和蓝色权益曲线相对于基准（红色权益曲线）的线性度。

Jensen的Alpha结果

这是第一个将蓝色净值曲线评为表现最佳策略的指标。当基准回报不好时，这个指标通常会奖励好的表现。即使绝对收益为负，Jensen的alpha也有可能表示正收益。当绝对基准回报率比所研究的回报率更差时，就会发生这种情况。因此，使用此指标时要小心。

Jensen 的 Alpha 的解释

如果Jensen的Alpha为正，则表明与基准相比，投资组合/策略产生了超额回报，这表明在考虑其风险水平后表现出色。否则，如果Jensen的Alpha为负值，则意味着该策略相对于基准回报表现不佳。

除了alpha值之外，最小二乘法计算的beta值还提供了回报相对于基准的敏感性的衡量标准。beta系数为1表示该策略的回报与基准同步。beta系数小于1表明净值曲线的波动性小于基准曲线，而beta系数大于1表明波动性更高

结论

我们已经描述了一些风险调整回报指标的实施，这些指标可以用作夏普比率的替代品。在我看来，最好的候选者是omega标准。它提供了夏普比率的相同优势，而没有任何收益分布正态性的预期。不过，还应该注意的是，在做出投资决策时，最好考虑多个策略绩效指标。只凭一个永远无法提供预期风险或回报的全貌。此外，请记住，大多数风险回报指标都提供了可追溯的衡量标准，历史表现并不能保证未来的结果。因此，在评估投资选择时，重要的是要考虑其他因素，如投资目标、时间范围和风险承受能力

所有指标的源代码都包含在PerformanceRatios.mqh中。应该指出的是，没有一项实现产生年度数字。所附的zip文件还包含用于可视化我们模拟的权益曲线的应用程序的代码。它是使用EasyAndFastGUI库实现的，该库可在mql5.com代码库中获得。这个库没有在这篇文章的附件中，文章所附的是EA的源代码和可工作编译好的版本。

文件名	描述
Mql5\Files\sp500close.csv	权益曲线计算中使用的SP500收盘价格的随附csv文件
Mql5\Include\PerformanceRatios.mqh	include文件，其中包含文章中描述的所有性能指标的定义
Mql5\Experts\EquityCurves.mq5	可视化工具的Expert advisor源代码，要进行编译，需要在代码库中提供 easyandfastgui 库
Mql5\Experts\EquityCurves.ext	这是EA的已编译版本