Alternative Risiko-Ertrags-Metriken in MQL5

Einführung

Alle Händler hoffen, die prozentuale Rendite ihrer Investition so weit wie möglich zu maximieren, aber höhere Renditen gehen in der Regel mit einem höheren Risiko einher. Dies ist der Grund, warum risikobereinigte Renditen das wichtigste Maß für die Performance in der Investmentbranche sind. Es gibt viele verschiedene Maßstäbe für die risikobereinigte Rendite, die jeweils ihre eigenen Vor- und Nachteile haben. Die Sharpe Ratio ist ein beliebtes Risiko- und Renditemaß, das dafür bekannt ist, dass es unrealistische Voraussetzungen an die zu analysierende Renditeverteilung stellt. Dies hat zwangsläufig zur Entwicklung alternativer Performancemetriken geführt, die die gleiche Allgegenwart wie die Sharpe-Ratio bieten sollen, ohne die Nachteile. In diesem Artikel stellen wir die Implementierung alternativer Risiko-Rendite-Metriken vor und erstellen hypothetische Aktienkurven, um ihre Eigenschaften zu analysieren.

Simulierte Aktienkurven

Um die Interpretierbarkeit zu gewährleisten, werden wir die Daten des SP 500 als Grundlage für eine simulierte Handelsstrategie verwenden. Wir verwenden keine spezifischen Handelsregeln, sondern setzen Zufallszahlen ein, um Aktienkurven und entsprechende Renditereihen zu generieren. Das Anfangskapital wird auf einen konfigurierbaren Betrag standardisiert. Die Zufallszahlen werden durch einen „Seed“ definiert, sodass jeder, der die Experimente reproduzieren möchte, dies tun kann.

Visualisierung von Aktienkurven

Die folgende Grafik zeigt eine Metatrader 5 (MT5) Anwendung, die als Expert Advisor (EA) implementiert ist und drei Aktienkurven anzeigt. Die rote Aktienkurve ist die Benchmark, von der die blaue und die grüne Aktienkurve abgeleitet werden. Der Benchmark kann durch die Konfiguration des Anfangskapitals verändert werden. Einstellbar über die Anwendung.  

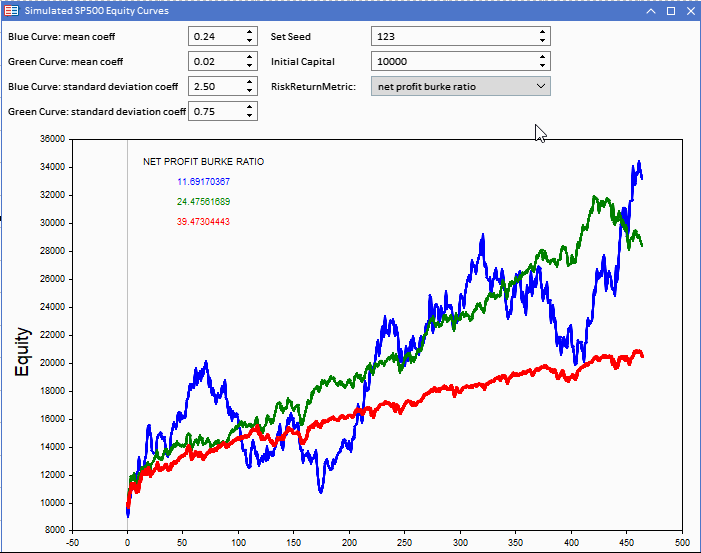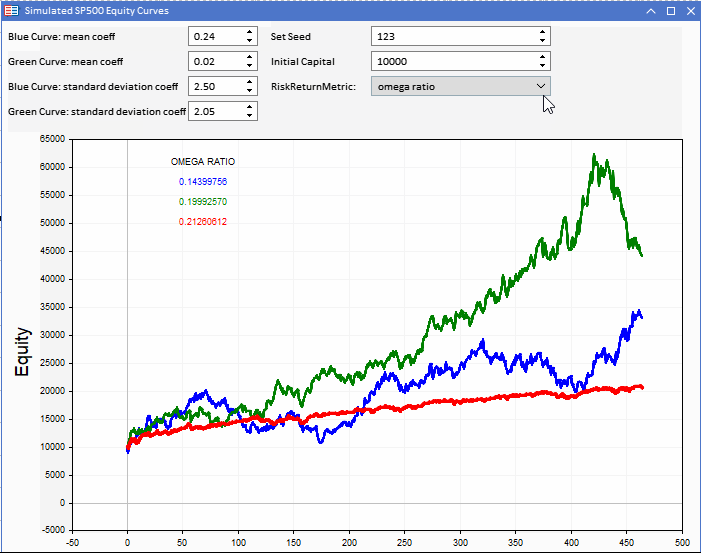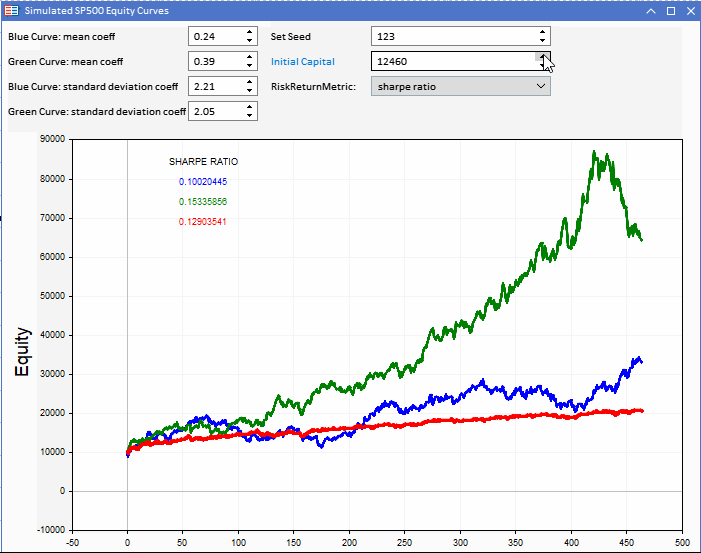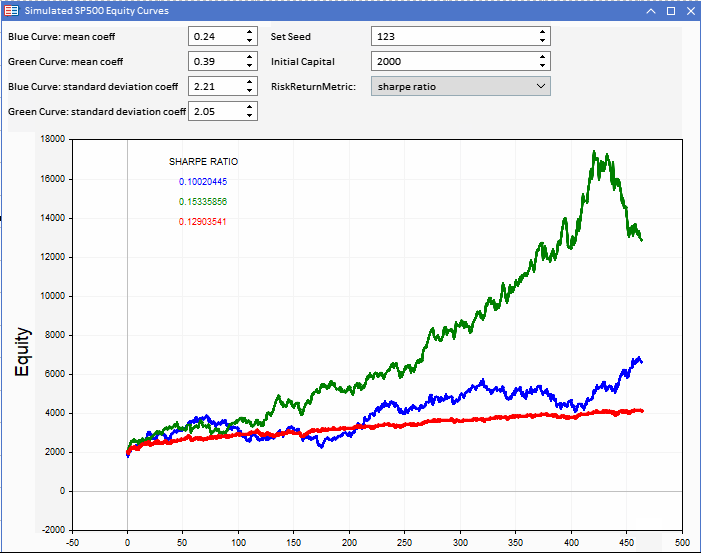
Die Aktienkurven werden auf der Grundlage der Benchmark-Reihen erstellt. Jede davon ist durch eine Zufallskomponente definiert, die durch zwei einstellbare Konstanten gesteuert werden kann, dem Mittelwert und der Standardabweichung. In Kombination mit der Standardabweichung der Benchmark-Renditen ergeben sich daraus die Parameter für die normalverteilten Zufallszahlen, die zur Erzeugung zweier hypothetischer Aktienkurven verwendet werden.   

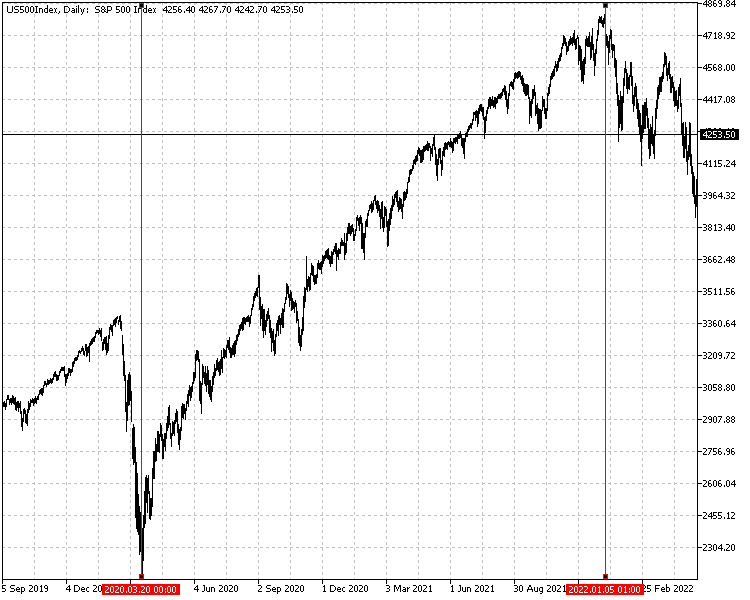
Zunächst berechnen wir die Renditen anhand der täglichen Schlusskurse des SP 500 aus dem Zeitraum zwischen dem 20. März 2020 und dem 5. Januar 2022 (einschließlich). Die Aktienkurve wird aus der Reihe der Renditen erstellt. Mit den Reihen, die das Eigenkapital und die Renditen definieren, werden wir die berechneten Leistungsergebnisse mit dem Aussehen einer bestimmten Aktienkurve vergleichen.

Der Code für die Anwendung ist dem Artikel beigefügt.

Drawdown-Zahlen

Der Drawdown ist der größte Betrag des Kapitals, den eine Strategie zwischen zwei beliebigen Zeitpunkten verloren hat. Dieser Wert gibt einen Hinweis auf das Risiko, das eine Strategie auf sich genommen hat, um ihre Gewinne zu erzielen, sofern diese überhaupt erzielt wurden. Wenn eine Reihe, die aus einer beliebigen Anzahl der höchsten Drawdowns besteht, zusammengezählt und aggregiert wird, kann das Ergebnis als Maß für die Variabilität verwendet werden.

Burke-Verhältnis

Im Jahr 1994 schrieb Burke einen Artikel mit dem Titel „A sharper sharpe ratio“, in dem er die Burke-Ratio als Alternative zur bekannten Sharpe Ratio vorstellte. Bei der Burke-Ratio wird der Nenner der Sharpe-Ratio-Formel durch die quadrierte Summe einer bestimmten Anzahl der höchsten absoluten Drawdowns ersetzt. Der Zähler kann entweder die mittlere Rendite oder die absolute monetäre Rendite der Strategie/des Portfolios, d. h. der Nettogewinn, sein. Schauen wir uns die beiden Versionen der Berechnung an. Wir unterscheiden zwischen der Burke-Ratio, die auf dem Nettogewinn basiert, und der Burke-Ratio, die auf den durchschnittlichen Erträgen basiert. Die Formeln sind unten angegeben.

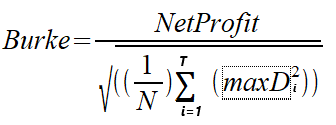
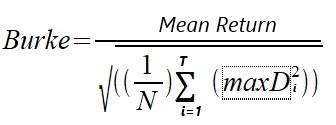
MaxD ist die Reihe der größten T absoluten Drawdowns, die aus den Aktienwerten berechnet werden. N steht für die Anzahl der in der Berechnung verwendeten Aktienwerte.

Der Nettogewinn der Burke-Ratio ist in Form der Funktion netprofit_burke() implementiert. Die Funktion benötigt ein Array von Aktienwerten, die die Aktienkurve beschreiben, sowie einen ganzzahligen Wert, der die Anzahl der höchsten Drawdowns angibt, die bei der Berechnung berücksichtigt werden sollen.

//+------------------------------------------------------------------+
//|Net profit based Burke ratio                                      |
//+------------------------------------------------------------------+
double netprofit_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
        {
         sumdd+=(outdd[i]*outdd[i]);
        }
      return (in_ec[insize-1]-in_ec[0])/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Wenn der Standardwert Null angegeben ist, verwendet die Funktion die Formel N/20, um die Anzahl der zu berücksichtigenden Drawdowns festzulegen, wobei N die Größe des Aktienarrays ist.

Um die angegebene Anzahl von Drawdowns zu sammeln, wird die Funktion MaxNDradowns() herangezogen. Sie gibt die Reihe der höchsten absoluten Drawdowns in aufsteigender Reihenfolge aus.

//+------------------------------------------------------------------+
//|Maximum drawdowns function given equity curve                     |
//+------------------------------------------------------------------+
bool MaxNDrawdowns(const int num_drawdowns,double &in_ec[],double &out_dd[])
  {
   ZeroMemory(out_dd);

   ResetLastError();

   if(num_drawdowns<=0)
     {
      Print("Invalid function parameter for num_drawdowns ");
      return false;
     }
   double u[],v[];

   int size = ArraySize(in_ec);

   if((ArrayResize(v,(size*(size-1))/2)< int((size*(size-1))/2))||
      (ArraySize(out_dd)!=num_drawdowns && ArrayResize(out_dd,num_drawdowns)<num_drawdowns))
     {
      Print(__FUNCTION__, " resize error ", GetLastError());
      return false;
     }

   int k=0;
   for(int i=0; i<size-1; i++)
     {
      for(int j=i+1; j<size; j++)
        {
         v[k]=in_ec[i]-in_ec[j];
         k++;
        }
     }

   ArraySort(v);

   for(int i=0; i<k; i++)
     {
      if(v[i]>0)
        {
         if(i)
           {
            if(!ArrayRemove(v,0,i))
              {
               Print(__FUNCTION__, " error , ArrayRemove: ",GetLastError());
               return false;
              }
            else
               break;
           }
         else
            break;
        }
     }

   size=ArraySize(v);

   if(size && size<=num_drawdowns)
     {
      if(ArrayCopy(out_dd,v)<size)
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      else
         return (true);
     }


   if(ArrayCopy(out_dd,v,0,size-num_drawdowns,num_drawdowns)<num_drawdowns)
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return false;
     }


   return(true);

  }

Die Berechnung der Burke-Ratio, bei der die mittleren Renditen im Zähler stehen, ist als Funktion meanreturns_burke implementiert und hat ähnliche Eingabeparameter.

//+------------------------------------------------------------------+
//|Mean return based Burke ratio                                     |
//+------------------------------------------------------------------+
double meanreturns_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double rets[];

   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(ArrayResize(rets,insize-1)<insize-1)
     {
      Print(__FUNCTION__," Memory allocation error ",GetLastError());
      return 0;
     }

   for(int i=1; i<insize; i++)
      rets[i-1] = (in_ec[i]/in_ec[i-1]) - 1.0;

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
         sumdd+=(outdd[i]*outdd[i]);
      return MathMean(rets)/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Verhältnis zwischen Nettogewinn und maximaler Inanspruchnahme

Die Formel der Burke-Ratio, die den Nettogewinn als Zähler verwendet, ähnelt dem Verhältnis zwischen Nettogewinn und maximalem Drawdown (NPMD). Der Unterschied besteht darin, dass bei der Berechnung des NPMD-Verhältnisses der höchste einzelne Drawdown zugrunde gelegt wird.

Die NPMD-Berechnung ist als Funktion netProfiMaxDD() implementiert, die das Array der Aktienwerte als Eingabe benötigt.

//+------------------------------------------------------------------+
//|Net profit to maximum drawdown ratio                              |
//+------------------------------------------------------------------+
double netProfiMaxDD(double &in_ec[])
  {
   double outdd[];
   int insize=ArraySize(in_ec);

   if(MaxNDrawdowns(1,in_ec,outdd))
      return ((in_ec[insize-1]-in_ec[0])/outdd[0]);
   else
      return 0;
  }

Die Drawdown-basierten Kennzahlen wurden eingeführt, um einige der gegen die Sharpe Ratio vorgebrachten Kritikpunkte zu beseitigen. Die Berechnungen bestrafen keine abnormalen oder großen Gewinne und sind vor allem nicht parametrisch. Die Verwendung von absoluten Drawdowns im Nenner ist zwar vorteilhaft, führt aber dazu, dass sowohl das Burke- als auch das NPMD-Verhältnis Strategien mit relativ geringen Abwärtsspitzen begünstigen.

Bezieht sich auf das Visualisierungstool für Aktienkurven. Die blaue Kurve weist die höchsten Renditen auf, hat aber eine niedrigere Punktzahl als die übrigen Kurven.

Die Benchmark-Werte für beide Kennzahlen verdeutlichen, wie irreführend die Metriken sein können, wenn sie zum Vergleich der Leistung von Strategien verwendet werden. Die Benchmark-Kennzahlen sind deutlich höher, obwohl die anderen Kurven mehr reale Rendite liefern.

Die Verwendung absoluter Drawdowns kann das Risiko im Vergleich zur Verwendung der Verteilung negativer Renditen, wie es bei der Sharpe Ratio der Fall ist, überbetonen.

Vergleicht man die Sharpe-Scores, so zeigt sich, dass die grüne Kurve den höchsten Wert aufweist, wobei der Unterschied zwischen den Ergebnissen der simulierten Strategien wesentlich geringer ist.

Interpretation der Drawdown-Werte

Je höher die Burke- oder NPMD-Werte ist, desto besser ist die risikoadjustierte Performance der Anlagestrategie. Das bedeutet, dass die Strategie im Vergleich zum eingegangenen Risiko höhere Erträge erzielt.

- Wenn das Burke- oder NPMD-Verhältnis größer als 0 ist, deutet dies darauf hin, dass die Anlagestrategie im Vergleich zum berechneten Risiko eine Überrendite liefert.

- Ist die Burke- oder NPMD-Quote kleiner als 0, deutet dies darauf hin, dass die Anlagestrategie im Vergleich zum eingegangenen Risiko keine ausreichende Überrendite erzielt.

Partielle Momentverhältnisse

Partielle momentbasierte Kennzahlen sind ein weiterer Versuch, eine Alternative zur Sharpe Ratio zu finden. Sie beruhen auf dem statistischen Konzept der Semi-Varianz und geben Aufschluss darüber, wie gut eine Strategie im Hinblick auf das Abwärtsrisiko (negative Renditen) im Vergleich zum Aufwärtspotenzial (positive Renditen) abschneidet. Um partielle Momentkennzahlen zu berechnen, müssen wir zunächst den partiellen Gewinn und den partiellen Verlust bestimmen. Diese Werte werden abgeleitet, indem ein Schwellenwert für die Rendite festgelegt wird, in der Regel die akzeptable Mindestrendite oder der risikofreie Zinssatz, und die Differenz zwischen der tatsächlichen Rendite und der Schwellenwertrendite für jede Beobachtung berechnet wird.

Bei der Berechnung können Differenzen ignoriert werden, die entweder über dem Schwellenwert für das untere partielle Moment oder unter dem Schwellenwert für das höhere partielle Moment (HPM) liegen. Das untere partielle Moment (LPM) misst die quadrierten Abweichungen der Renditen, die unter den Schwellenwert fallen, während das höhere partielle Moment (HPM) die quadrierten Abweichungen der Renditen misst, die den Schwellenwert überschreiten. Partielle Momente bieten eine alternative Risikoperspektive im Vergleich zu Drawdown-Ratios, indem sie sich auf das Risiko konzentrieren, das mit Renditen verbunden ist, die entweder unter oder über einer bestimmten Schwelle liegen.

Nachstehend finden Sie die Formeln für die LPM bzw. HPM:

Dabei ist thresh der Schwellenwert, x eine beobachtete Rendite und max bestimmt den Maximalwert zwischen der sich ergebenden Differenz und Null, bevor er zur Potenz von n erhoben wird. n definiert den Grad eines partiellen Moments. Wenn n=0 ist, gibt das LPM die Wahrscheinlichkeit an, dass eine Beobachtung unter dem Schwellenwert liegt, und das HPM die Wahrscheinlichkeit, dass sie darüber liegt. N ist die Anzahl der beobachteten Erträge. Zwei partielle Momentkennzahlen, die wir betrachten werden, sind das verallgemeinerte Omega und das Upside-Potential-Verhältnis (UPR).

Omega

Das verallgemeinerte Omega wird durch einen einzelnen n-Grad-Term und einen Schwellenwert definiert, der die für die Berechnung verwendete LPM festlegt.

Die Funktion omega() implementiert die Berechnung des Omega-Verhältnisses, indem sie als Eingabe ein Array von Rückgaben erhält. Die Funktion verwendet ein unteres partielles Moment vom Grad 2, wobei der Schwellenwert als Null angenommen wird.

//+------------------------------------------------------------------+
//|omega ratio                                                       |
//+------------------------------------------------------------------+
double omega(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);

   if(pmomentl)
      return MathMean(rt)/pmomentl;
   else
      return 0;
  }

Verhältnis des Aufwärtspotenzials

Die UPR verwendet zwei n-Grad-Terme (n1 und n2 in der Formel) und einen Schwellenwert. n1 bestimmt den HPM-Grad im Zähler und n2 gibt den LPM-Grad des Nenners an.

Ähnlich wie bei der Implementierung der Omega-Performance-Metrik berechnet die Funktion upsidePotentialRatio() das UPR-Verhältnis. Bei der Berechnung werden auch partielle Momente vom Grad 2 verwendet, und der Schwellenwert wird auf Null gesetzt.

//+------------------------------------------------------------------+
//|Upside potential ratio                                            |
//+------------------------------------------------------------------+
double upsidePotentialRatio(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentu=MathPow(partialmoment(2,rt,rb,true),0.5);
   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);
   if(pmomentl)
      return pmomentu/pmomentl;
   else
      return 0;
  }

Die Berechnung von partiellen Momenten wird mit der Funktion partialmoment() durchgeführt. Sie benötigt als Eingabe den Grad des Moments als Ganzzahl ohne Vorzeichen, zwei Arrays vom Typ Double und einen booleschen Wert. Das erste Array sollte die beobachteten Renditen und das zweite die Schwellenwerte oder Benchmark-Renditen enthalten, die für die Berechnung verwendet werden. Der boolesche Wert bestimmt die Art des zu berechnenden partiellen Moments, entweder true für das höhere partielle Moment und false für das untere partielle Moment.

//+------------------------------------------------------------------+
//|Partial Moments                                                   |
//+------------------------------------------------------------------+
double partialmoment(const uint n,double &rt[],double &rtb[],bool upper=false)
  {
   double pm[];
   int insize=ArraySize(rt);

   if(n)
     {
      if(ArrayResize(pm,insize)<insize)
        {
         Print(__FUNCTION__," resize error ", GetLastError());
         return 0;
        }

      for(int i=0; i<insize; i++)
         pm[i] = (!upper)?MathPow(MathMax(rtb[i]-rt[i],0),n):MathPow(MathMax(rt[i]-rtb[i],0),n);
      return MathMean(pm);
     }
   else
     {
      int k=0;
      for(int i=0; i<insize; i++)
        {
         if((!upper && rtb[i]>=rt[i]) || (upper && rt[i]>rtb[i]))
           {
            ArrayResize(pm,k+1,1);
            pm[k]=rt[i];
            ++k;
           }
         else
            continue;
        }

      return MathMean(pm);

     }

  }

Betrachtet man die Omega- und UPR-Kennzahlen unserer Aktienkurven, so fällt die Ähnlichkeit der Bewertung mit der Sharpe-Ratio auf.

Auch hier wird Beständigkeit gegenüber den volatileren Aktienkurven bevorzugt. Insbesondere Omega scheint eine brauchbare Alternative zur Sharpe Ratio zu sein.

Interpretation des partiellen Momentenverhältnisses

Omega ist in Bezug auf seine Auslegung im Vergleich zum UPR sehr viel eindeutiger. Je höher der Omega-Wert, desto besser. Negative Werte weisen auf Strategien hin, bei denen Geld verloren geht, während positive Werte auf eine Performance hindeuten, die im Verhältnis zum eingegangenen Risiko Überrenditen liefert.

Die UPR hingegen kann ein wenig seltsam sein, wenn es um die Interpretation geht. Sehen Sie sich einige simulierte Aktienkurven mit abweichenden Leistungsprofilen an.

Die blaue Aktienkurve zeigt negative Renditen, aber das UPR-Ergebnis ist positiv. Noch merkwürdiger sind die Ergebnisse der grünen und roten Aktienkurven. Die Kurven selbst sind fast ähnlich, wobei die grüne Aktienkurve die besseren Renditen erzielt, der UPR-Wert jedoch geringer ist als der der roten Kurve.

Regressionsanalyse der Renditen - Jensen's Alpha

Die lineare Regression ermöglicht die Konstruktion einer Linie, die am besten zu einem Datensatz passt. Regressionsbasierte Metriken messen daher die Linearität von Aktienkurven. Jensen's Alpha berechnet den Wert von Alpha in der Standardregressionsgleichung. Sie quantifiziert die Beziehung zwischen den Benchmark-Renditen und den beobachteten Renditen.

Um den Wert von Alpha zu berechnen, können wir die Methode der kleinsten Quadrate anwenden. Die Funktion leastsquarefit() nimmt als Eingabe zwei Arrays, die die Antwort und den Prädiktor definieren. In diesem Zusammenhang wäre die Antwort eine Reihe von beobachteten Renditen und der Prädiktor ist die Reihe von Benchmark-Renditen. Die Funktion gibt die Alpha- und Beta-Werte aus, deren Referenzen beim Aufruf der Funktion angegeben werden müssen.

//+------------------------------------------------------------------+
//|linear model using least squares fit y=a+bx                       |
//+------------------------------------------------------------------+
double leastsquaresfit(double &y[],double &x[], double &alpha,double &beta)
  {
   double esquared=0;

   int ysize=ArraySize(y);
   int xsize=ArraySize(x);

   double sumx=0,sumy=0,sumx2=0,sumxy=0;

   int insize=MathMin(ysize,xsize);

   for(int i=0; i<insize; i++)
     {
      sumx+=x[i];
      sumx2+=x[i]*x[i];
      sumy+=y[i];
      sumxy+=x[i]*y[i];
     }

   beta=((insize*sumxy)-(sumx*sumy))/((insize*sumx2)-(sumx*sumx));
   alpha=(sumy-(beta*sumx))/insize;

   double pred,error;

   for(int i=0; i<insize; i++)
     {
      pred=alpha+(beta*x[i]);
      error=pred-y[i];
      esquared+=(error*error);
     }

   return esquared;

  }

Wendet man Jensens Alpha auf unsere simulierten Aktienkurven an, erhält man ein Maß für die Linearität der grünen und blauen Aktienkurven im Vergleich zur Benchmark (rote Aktienkurve).

Dies ist die erste Kennzahl, die die blaue Aktienkurve als die leistungsstärkste Strategie bewertet. Diese Kennzahl belohnt in der Regel eine gute Leistung, wenn die Benchmark-Renditen schlecht sind. Es ist möglich, dass Jensens Alpha positive Renditen anzeigt, auch wenn die absoluten Renditen negativ sind. Dies kann passieren, wenn die absoluten Benchmark-Renditen einfach schlechter sind als die untersuchten Renditen. Seien Sie also vorsichtig bei der Verwendung dieses Maßstabs.

Jensens Alpha Interpretation

Ein positives Jensen-Alpha deutet darauf hin, dass das Portfolio/die Strategie im Vergleich zu einer Benchmark Überrenditen erwirtschaftet hat, was auf eine Outperformance unter Berücksichtigung des Risikoniveaus hindeutet. Ist das Jensen-Alpha negativ, bedeutet dies, dass die Strategie im Vergleich zu den Benchmark-Renditen eine unterdurchschnittliche Leistung erbracht hat.

Neben dem Alpha-Wert liefert der Beta-Wert aus der Berechnung der kleinsten Quadrate ein Maß für die Empfindlichkeit der Renditen gegenüber der Benchmark. Ein Beta von 1 bedeutet, dass sich die Renditen der Strategie synchron mit der Benchmark entwickeln. Ein Beta kleiner als 1 deutet darauf hin, dass die Aktienkurve weniger volatil ist als die der Benchmark, während ein Beta größer als 1 auf eine höhere Volatilität hindeutet.

Schlussfolgerung

Wir haben die Umsetzung einiger risikobereinigter Renditemetriken beschrieben, die als Alternative zur Sharpe Ratio verwendet werden können. Meiner Meinung nach ist der beste Kandidat die Omega-Metrik. Sie bietet dieselben Vorteile wie Sharpe Ratio, ohne dass eine Normalitätserwartung für die Renditeverteilung besteht. Es ist jedoch auch anzumerken, dass es besser ist, bei Investitionsentscheidungen mehrere Leistungsindikatoren der Strategie zu berücksichtigen. Man wird nie in der Lage sein, ein vollständiges Bild des erwarteten Risikos oder der erwarteten Rendite zu vermitteln. Denken Sie auch daran, dass die meisten Risiko- und Renditemessungen retrospektiv sind und dass die historische Performance keine Garantie für zukünftige Ergebnisse ist. Daher ist es wichtig, bei der Beurteilung von Anlageoptionen auch andere Faktoren wie Anlageziele, Zeithorizont und Risikotoleranz zu berücksichtigen.

Der Quellcode für alle Metriken ist in PerformanceRatios.mqh enthalten. Es ist anzumerken, dass keine der Implementierungen annualisierte Zahlen liefert. Die beigefügte Zip-Datei enthält auch den Code für die Anwendung, die zur Visualisierung unserer simulierten Aktienkurven verwendet wird. Sie wurde mit Hilfe der EasyAndFastGUI-Bibliothek implementiert, die unter mql5.com in der CodeBase verfügbar ist. Die Bibliothek ist dem Artikel nicht beigefügt. Im Anhang finden Sie den Quellcode des EA und eine funktionierende kompilierte Version.

Dateiname	Beschreibung
Mql5\Files\sp500close.csv	eine beigefügte csv-Datei mit den SP500-Schlusskursen, die für die Berechnung der Aktienkurven verwendet wurden
Mql5\Include\PerformanceRatios.mqh	Include-Datei, die die Definition aller im Artikel beschriebenen Leistungsmetriken enthält
Mql5\Experts\EquityCurves.mq5	Expert Advisor-Quellcode für das Visualisierungstool, für dessen Kompilierung die in der Codebasis verfügbare einfache und schnelle Benutzeroberfläche erforderlich ist
Mql5\Experts\EquityCurves.ex5	Dies ist die kompilierte Version des EA