Одномерный сингулярный спектральный анализ

Введение

Финансовые рынки характеризуются высокой волатильностью и сложными динамическими процессами, что делает прогнозирование и выявление закономерностей крайне сложной задачей. Сингулярный спектральный анализ (SSA) представляет собой эффективный метод анализа временных рядов, который позволяет представить сложную структуру ряда в виде разложения на простые компоненты, такие как тренд, сезонные (периодические) колебания и шум. Метод SSA, основанный на линейной алгебре, не требует предположений о стационарности, что делает его универсальным инструментом для исследования структуры временных рядов. 

Однако, широкое использование теории векторной и матричной алгебры в литературе по SSA создает довольно высокий порог вхождения, что может затруднить понимание темы у неподготовленных читателей и помешать им разобраться во всех тонкостях и преимуществах этого метода анализа. Данная статья стремится доступно и ясно изложить теоретические основы SSA, без понимания которых, метод становится «черным ящиком», а также предоставить практическую реализацию описанных концепций. 

Необходимо уточнить, что под термином SSA следует понимать целое семейство методов анализа, но все они основаны на последовательном применении четырех шагов:

• преобразование временного ряда в траекторную матрицу (Ганкелеву матрицу),
• разложение траекторной матрицы на сумму элементарных матриц ранга один,
• группировку элементарных матриц,
• восстановление (реконструкцию) временного ряда.

Рассмотрим подробнее каждый из этих этапов.

Построение траекторной матрицы

Основная идея состоит в том, чтобы преобразовать временной ряд в матрицу, которая будет отражать его структуру в многомерном  пространстве. Это делается для того, чтобы выявить скрытые зависимости между последовательными значениями ряда. Траекторную матрицу строят следующим образом. Берут одномерную выборку временного ряда объёма N и трансформируют ее в набор из K векторов (K= N – L + 1) через составление скользящих подвыборок объёма L (длина окна). Получившиеся вектора длиной L(x1,x2,...,xL},{x2,x3,...,xL+1}и т. д.), располагают в столбцах траекторной матрицы X.

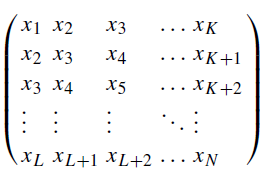
Рис.1 Траекторная матрица X

Здесь параметр L определяет глубину анализа. Обычно его устанавливают равным N/2.

Разложение траекторной матрицы на сумму матриц ранга один

После построения траекторной матрицы, выполняют ее разложение. Когда в качестве такого разложения выступает сингулярное разложение (SVD) траекторной матрицы, то такой метод анализа называется базовым (Basic-SSA).

С помощью сингулярного разложения составляются так называемые собственные тройки (√λi, Ui, Vi), где

• σi = √λi — сингулярные значения, равные корню из собственных чисел матрицы XX',
• Ui — левые сингулярные вектора,
• Vi — правые сингулярные вектора,
• i — количество сингулярных значений, равное рангу траекторной матрицы X.

Сингулярные числа σi показывают вес каждой компоненты, при этом, большие значения соответствуют важным закономерностям (тренд, циклы), малые значения — шуму.

Таким образом, с помощью разложения SVD, траекторную матрицу можно представить в виде суммы элементарных матриц Xi ранга один:

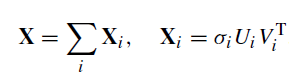
Матрицы ранга один — это «кирпичики», из которых строятся более сложные матрицы.

Поясним понятие ранга матрицы в контексте метода SSA. SSA нацелен на выделение детерминированного сигнала из временного ряда. Детерминированные последовательности, такие как экспонента, полином или синусоида, характеризуются конечным рангом. Это обусловлено тем, что они удовлетворяют линейным рекуррентным соотношениям (LRR), а их траекторные матрицы содержат ограниченное число линейно независимых векторов. Например, траекторная матрица экспоненциальной последовательности имеет ранг 1 (только один линейно независимый вектор), синусоиды — ранг 2, полинома степени (k) — ранг k+1 и так далее.

Скрипт Rank, демонстрирующий понятие ранга детерминированных рядов:

//+------------------------------------------------------------------+
//|                                                         Rank.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs

input int         N  = 100;                // N - length of generated time series
input int         L  = 30;                 // L - window length
input int         T  = 22;                 // T - period length of sine function
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   matrix X=matrix::Zeros(L,N-L+1);
   vector x_exp= vector::Zeros(N);
   vector x_sinus= vector::Zeros(N);
   vector x_polynom= vector::Zeros(N);
   for(int t=0; t <N; t++)
     {
      x_exp[t] = MathPow(1.01,t);           // 1. Экспоненциальная последовательность: x_t = 1.01^t
      x_sinus[t] = MathSin(2*M_PI*t/T);     // 2. Синусоида: x_t = sin(2 * pi * t / T)
      x_polynom[t] =  1 + t+ MathPow(t,2);  // 3. Полином степени 2: x_t = 1 + t + t^2
     }
   trajectory_matrix(x_exp,L,X);
   Print("Rank Exponential sequence = ",Rank_SVD(X));
   trajectory_matrix(x_sinus,L,X);
   Print("Rank Sinus sequence = ",Rank_SVD(X));
   trajectory_matrix(x_polynom,L,X);
   Print("Rank Polynom sequence = ",Rank_SVD(X));
  }
//+------------------------------------------------------------------+
//| Траекторная матрица X                                            |
//+------------------------------------------------------------------+
void trajectory_matrix(vector & series,int window_length, matrix & X)
  {
   int N_ = (int)series.Size();
   int L_ = window_length;
   int K = N_ - L_ + 1;
   X=matrix::Zeros(L_,K);
   for(int i=0; i <L_;  i++)
     {
      for(int j=0; j <K;  j++)
        {
         X[i,j] = series[i+j];
        }
     }
  }
//+------------------------------------------------------------------+
//|Finds the rank of a matrix using SVD                              |
//+------------------------------------------------------------------+
int Rank_SVD(matrix & X)
  {
   vector sv;
   matrix U,V;
   double tol = 1e-8;  // Порог для ненулевых значений
   X.SingularValueDecompositionDC(SVDZ_N,sv,U,V);
   double threshold = tol * sv.Max();
   int rank=0;
   for(int i=0; i<(int)sv.Size(); i++)
     {
      if(sv[i] > threshold)
         rank++;
     }
   return rank;
  }
//+------------------------------------------------------------------+

Реальные временные ряды, такие как биржевые цены, не являются последовательностями конечного ранга из-за присутствия шума, что делает их рядами полного ранга = min(L, K). Однако, если ряд представляет собой сумму детерминированного сигнала конечного ранга и шума, метод SSA способен приблизительно выделить этот сигнал. Далее прогнозирование выполняется только для детерминированной компоненты, а шум отбрасывается. Для этого, траекторную матрицу (X) раскладывают на элементарные матрицы ранга 1, из которых затем формируют более сложные матрицы, соответствующие полезному детерминированному сигналу. В этом заключается ключевая идея метода SSA.

Группировка

На шаге группировки элементарные матрицы ранга один объединяются в группы, которые интерпретируются, как различные компоненты ряда (тренд, сезонность, шум). Один из самых распространенных способов — сгруппировать матрицы на основе близости сингулярных значений матрицы X. После того, как определяют m непересекающихся групп I, разложение траекторной матрицы X можно записать в виде:

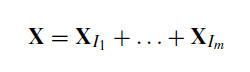
Например:

• Itrend = {1} — для тренда,
• Iseasonal = {2,3} — для сезонности,
• Inoise = {4....,i} — для шума,
  где i = количество сингулярных значений.

Графическое представление левых сингулярных векторов полезно для визуальной оценки наличия детерминированного сигнала. Например, если временной ряд содержит тренд, соответствующий сингулярный вектор будет отображать плавно изменяющуюся траекторию. При наличии периодической компоненты, пара сингулярных векторов (поскольку периодический сигнал имеет ранг 2) будет напоминать синусоиды. Сингулярные вектора, визуально схожие с гауссовским белым шумом и связанные с малыми сингулярными значениями, соответствуют шумовой компоненте. Эти свойства позволяют выполнять группировку компонент на основе визуального анализа сингулярных векторов.

Восстановление (реконструкция) временного ряда

Следующий шаг — перевод каждой получившейся сгруппированной матрицы в новый временной ряд длины N с использованием диагонального усреднения (diagonal averaging):

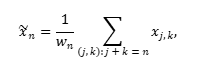
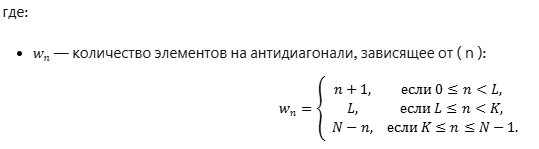
а, xj,k — элементы сгруппированной(или элементарной) матрицы.

Реконструированный таким образом временной ряд будет отвечать либо за тренд, либо за периодическую составляющую. Сумма этих рядов представляет собой непараметрическую модель исходного временного ряда, которая зависит от длины окна L и способа группировки элементарных матриц. При этом сумма всех реконструированных рядов (включая шум) полностью восстановит исходный временной ряд.

Прогнозирование

Прогноз значений временного ряда gi на M шагов вперед в методе SSA осуществляется на основе реконструированного ряда, используя линейную рекуррентную формулу:

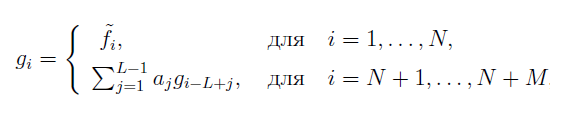
где:

• aj  — коэффициенты рекуррентного соотношения LRR (Linear Recurrence Relation),
• fi  — значения восстановленного ряда.

Вектор коэффициентов aj определяется на основе сингулярных векторов Ui:

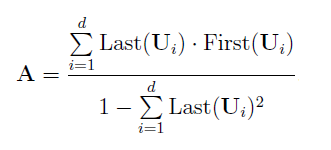
где:

• First : первые 𝐿 − 1 координат сингулярного вектора Ui,
• Last : последняя координата сингулярного вектора Ui,
• 𝑑 — количество выбранных сингулярных векторов представляющих полезный сигнал
  

Toeplitz-SSA

Существует еще один вариант SSA, отличающийся от традиционного подхода. В отличие от базового SSA, который использует траекторную матрицу, основанную на скользящем окне временного ряда, Toeplitz-SSA строит автоковариационную матрицу с тёплицевой структурой (отсюда и название метода). После чего, выполняется SVD разложение для автоковариационной матрицы. Метод группировки, диагональное усреднение, нахождение коэффициентов LRR, прогнозирование происходят точно так же, как и в базовом SSA.

Toeplitz-SSA лучше подходит для анализа стационарных временных рядов (он дает меньшую ошибку прогноза по сравнению с базовым). Однако, для нестационарных рядов классический SSA демонстрирует лучшие результаты. Так как на биржевых рынках нам приходится иметь дело с нестационарными процессами, то я решил ограничиться в данной статье только базовым алгоритмом.

Пример анализа Basic-SSA

Перейдём от теории к практической реализации описанных концепций на языке MQL5. Для этого подготовлен скрипт, генерирующий четыре синтетических временных ряда:

• синус + гауссовский белый шум,
• линейный тренд + синус + гауссовский белый шум,
• симметричное гауссовское случайное блуждание,гауссовский белый шум.
  

Эти ряды имеют следующие характеристики:

• Первый ряд — стационарный, с периодической компонентой,
• Второй ряд — нестационарный, с детерминированным трендом и периодической компонентой,
• Третий — нестационарный ряд со стохастическим трендом,
• Четвертый — стационарный белый шум.
  
  

Данные модели частично охватывают спектр временных рядов, встречающихся в реальных задачах.

Скрипт генерирует по выбору один синтетический ряд и последовательно реализует шаги, которые мы с вами рассмотрели выше, а также выводит на монитор следующие графики:

• сгенерированные данные,
• относительные сингулярные значения (доля дисперсии каждой сингулярной тройки),
• первые два сингулярных вектора,
• диаграмму рассеяния первых двух сингулярных векторов,
• ряд данных + его реконструкция + прогнозирование,
• реконструкция + прогноз с помощью функции MQL5SingularSpectrumAnalysisForecast.
  
  

График относительных сингулярных спектральных значений (доля квадрата сингулярного значения от суммы квадратов всех сингулярных значенийσi^2/∑ σj^2 — рис.2) позволяет определить тип компонент, который присутствует во временном ряде, и выбрать количество сингулярных троек для реконструкции сигнала. Обычно выбирают компоненты до точки резкого спада (так называемый "локоть" на графике).

Для периодической компоненты должно присутствовать два близких по величине сингулярных значения. Может присутствовать также плато с последующим спадом. Это означает присутствие нескольких гармонических компонент (синусоиды с разными частотами), за которыми следует шум.

Плавное убывание значений спектра говорит об отсутствии детерминированного сигнала.

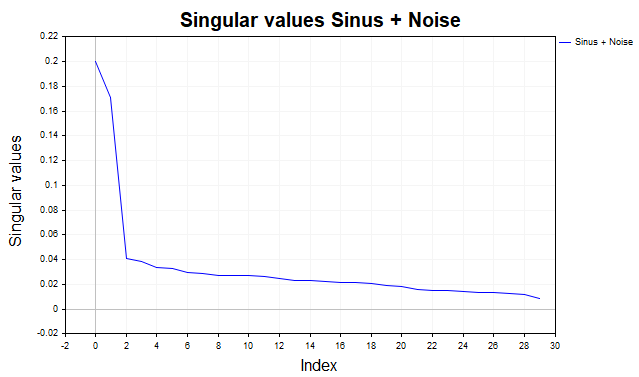
Рис.2 Относительный спектр, sinus+noise

Здесь стоит сказать о недостатке SSA, который заключается в неспособности отличить стохастический тренд от детерминированного. Например, для ряда случайного блуждания мы будем иметь только одну выраженную компоненту, которая отвечает за тренд. Но мы все знаем, что этот тренд случайный и непредсказуемый. Специально для проверки этого случая, я включил данные для случайного блуждания.

После выявления нескольких наибольших сингулярных значений, полезно изучить графики соответствующих левых сингулярных векторов (рис.3). Для периодического сигнала, смешанного с шумом, первые два сингулярных вектора, связанные с наибольшими сингулярными значениями, обычно имеют форму, близкую к синусоиде или косинусоиде, отражая периодическую природу сигнала.

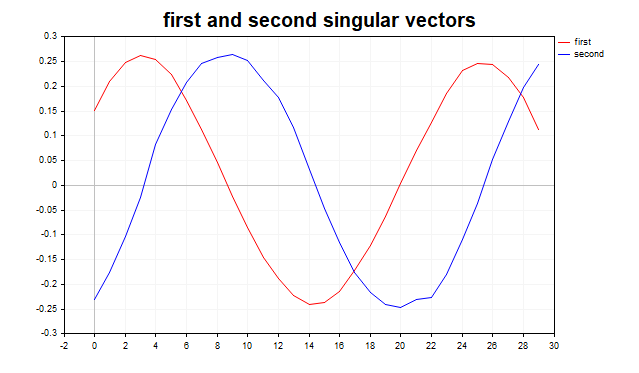
Рис.3 Первые два сингулярных вектора, sinus+noise

Дополнительно можно построить график рассеяния для пары сингулярных векторов, где по оси (x) откладывается, например, первый сингулярный вектор (U1), а по оси (y) — второй (U2). (рис.4)

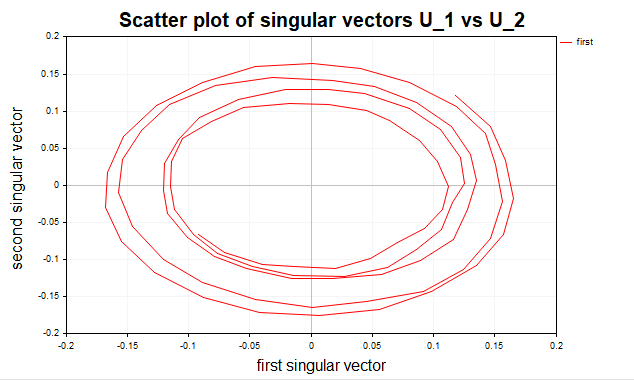
Рис.4 Диаграмма рассеяния первых двух сингулярных векторов, sinus+noise

Если данные содержат циклические компоненты, диаграмма рассеяния часто принимает форму эллипса или окружности, что подтверждает синусоидальный характер сигнала. Это связано с тем, что пара сингулярных векторов для периодической компоненты соответствует двум ортогональным гармоникам (например, синусу и косинусу). Если точки на графике рассеяния формируют хаотичное облако без чёткой геометрической структуры, это указывает на отсутствие выраженной периодической или детерминированной компоненты.

На рис.5 показан синтетический ряд sinus+noise, его реконструкция и прогноз на 100 шагов вперед. Визуально определить наличие периодического сигнала в исходных данных затруднительно из-за сильного шума, однако SSA эффективно выделяет периодическую компоненту. Конечно, это очень простой пример, и в реальных финансовых данных такая чёткая картина встречается редко. Тем не менее, SSA дает прекрасную возможность подтвердить или опровергнуть гипотезу присутствия циклов в ценах.

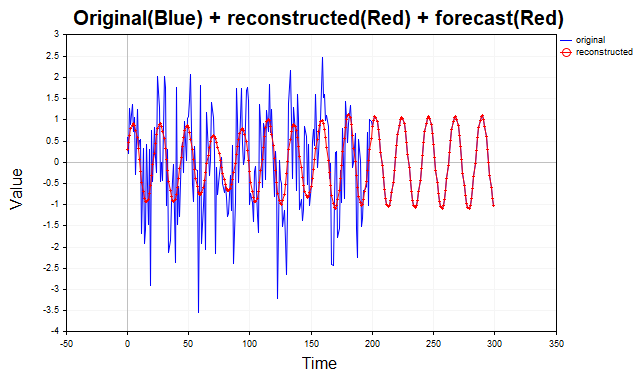
Рис.5 Прогноз ряда sinus+noise

Реализация SSA в MQL5

Остановимся на уже существующих реализациях SSA в MQL5. В поставке терминала идет функция SingularSpectrumAnalysisForecast из раздела Методы матриц и векторов\OpenBLAS. Из описания этой функции мне было не совсем ясно, какой именно вид SSA в ней реализован.

Изначально я предполагал, что это вариант Toeplitz-SSA, основанный на разложении автоковариационной матрицы. Но так как результаты прогноза и реконструкции ряда по скрипту Basic-SSA и по функции SingularSpectrumAnalysisForecast полностью совпали, то наверное, это все-таки реализация базового алгоритма. В качестве примера, приведу график прогноза ряда trend+sinus+noise по трем главным компонентам (рис.6). Анализируемый ряд состоит из 200 значений, прогноз делаем на 100 шагов вперед.

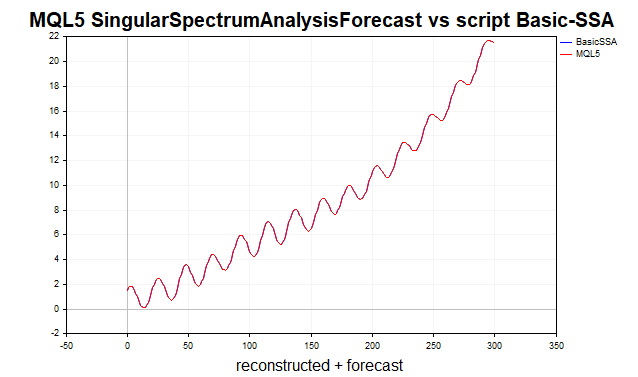
Рис.6  Ряд реконструкции и прогноза MQL5 vs BasicSSA

Для разложения траекторной матрицы я использовал функцию SingularValueDecompositionDCиз того же раздела OpenBLAS, так как разработчики позиционируют алгоритм "разделяй и властвуй" (divide and conquer)^ как самый быстрый среди других алгоритмов SVD. Очень удобно, что данная функция позволяет рассчитывать, как полные, так и усеченные матрицы сингулярных векторов.

Код скрипта Basic-SSA:

//+------------------------------------------------------------------+
//|                                                    Basic-SSA.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Math\Stat\Stat.mqh>
#include <Graphics\Graphic.mqh>

enum SimpleData
  {
   SinusPlusNoise,
   Trend_Sinus_Noise,
   RandomWalk,
   WhiteNoise,
  };

input int         L  = 30;                 // L - window length
input int         N  = 200;                // N - length of generated time series
input int         T  = 22;                 // T - period length of sine function
input int         fs = 100;                // fs - forecast horizon
input int         r_ = 2;                  // r - singular components
input SimpleData  sd = SinusPlusNoise;     // Data
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int err;
   vector x = vector::Zeros(N); // time series
   double x_array[];
   double original_series[];
//------------1. Данные --------------------
//------------------ sinus + noise ---------
   if(sd == SinusPlusNoise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] = MathSin(2*M_PI*(i+1)/T) + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//------------------trend + sinus + noise ----
   if(sd == Trend_Sinus_Noise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] =  0.05 * i + MathSin(2*M_PI*(i+1)/T) + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//-------------- random walk -----------------
   if(sd == RandomWalk)
     {
      x[0]=100;
      for(int i=1; i <N;  i++)
        {
         x[i] = x[i-1] + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//-------------- white noise -----------------
   if(sd == WhiteNoise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] = MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1); // график белого шума
     }
//------------2. Траекторная матрица -------------------
   matrix X;
   trajectory_matrix(x,L,X);
//-------------3. Cингулярное разложение (SVD) ----
   matrix U, V;
   vector singular_values;
   X.SingularValueDecompositionDC(SVDZ_A,singular_values,U,V);
   V = V.Transpose();
   double total_variance;
   vector powv = singular_values*singular_values;
   total_variance = powv.Sum();
   VectortoArray(powv/total_variance,x_array);
   PlotGraphic(x_array,5,2); // График  сингулярного спектра
   double x_1[],x_2[];
   VectortoArray(U.Col(0),x_1);
   VectortoArray(U.Col(1),x_2);
   PlotGraphic(x_1,x_2,5,3); // график первых двух сингулярных векторов
   PlotGraphic(x_1,x_2,5,4); // диаграмма рассеяния первых двух сингулярных векторов
//---------- 4. Реконструкция временного ряда----
   int K = N - L + 1;
   matrix X_i = matrix::Zeros(L,K);
   matrix Ui = matrix::Zeros(L,1);
   matrix Vi = matrix::Zeros(1,K);
   vector x_tilde;
   vector recon_series = vector::Zeros(N);
   for(int i=0; i<r_;i++)
     {
      Ui.Col(U.Col(i),0);
      Vi.Row(V.Col(i),0);
      X_i = (Ui.MatMul(Vi))*singular_values[i];  // матрицы ранга один
      diagonal_averaging(X_i,x_tilde);
      recon_series = recon_series + x_tilde;     // реконструированный ряд
     }
   double recon[];
   VectortoArray(recon_series,recon);

//------------5. Вектор коэффициентов LRR   --------------------
   matrix U_r = U;
   U_r.Resize(L,r_);              // r левых сингулярных векторов
   vector a = vector::Zeros(L-1); // вектор а коэффициентов LRR
   double denom =0;
   vector u_k;
   double last;
   for(int k=0; k<r_;k++)
     {
      u_k = U_r.Col(k);           //  k-ый сингулярный вектор
      last = u_k[L-1];
      u_k.Resize(L-1);
      a = a + last*u_k;
      denom = denom + MathPow(last,2);
     }
   denom = 1 - denom;
   a = a/denom;                   // вектор а коэффициентов LRR

//----------------- 6. Прогноз с использованием LRR-коэффициентов -----------
   int forecast_steps = fs;
   double forecast[];
   ArrayResize(forecast,forecast_steps);
   double fi[];
   ArrayCopy(fi,recon,0,N-L+1,L-1);
   for(int i=0;i<forecast_steps;i++)
     {
      double sum = 0.0;
      for(int j = 0; j < L-1; j++)
        {
         sum += a[j] * fi[j];
        }
      forecast[i]= sum;  // Прогноз
      // Обновляем fi
      ArrayCopy(fi, fi, 0, 1, ArraySize(fi)-1); // Сдвигаем влево
      fi[L-2] = forecast[i];                    // Добавляем новое значение
     }

   double originalplusforecast[];
   ArrayResize(originalplusforecast,N+forecast_steps);
   ArrayCopy(originalplusforecast,original_series,0,0,WHOLE_ARRAY);
   ArrayCopy(originalplusforecast,forecast,N,0,WHOLE_ARRAY);

   double reconstructedplusforecast[];
   ArrayResize(reconstructedplusforecast,N+forecast_steps);
   ArrayCopy(reconstructedplusforecast,recon,0,0,WHOLE_ARRAY);
   ArrayCopy(reconstructedplusforecast,forecast,N,0,WHOLE_ARRAY);
   PlotGraphic(originalplusforecast,reconstructedplusforecast,15,5);

//----реконструированные данные и прогноз по функции SingularSpectrumAnalysisForecast
   vector MQLreconforecast;
   x.SingularSpectrumAnalysisForecast(L,r_,forecast_steps,MQLreconforecast);
   double MQL_RF[];
   VectortoArray(MQLreconforecast,MQL_RF);
   PlotGraphic(reconstructedplusforecast,MQL_RF,10,6);
  }

//+------------------------------------------------------------------+
//| Plot Graphic                                                     |
//+------------------------------------------------------------------+
void PlotGraphic(double &data[], int sec, int n_graph)
  {
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   ulong width = ChartGetInteger(0,CHART_WIDTH_IN_PIXELS);
   ulong height = ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS);

   if(ObjectFind(0,"Graphic")<0)
      graphic.Create(0,"Graphic",0,0,0,int(width),int(height));
   else
      graphic.Attach(0,"Graphic");

   string st;
   if(sd == SinusPlusNoise)
     {
      st = "Sinus + Noise";
     }
   if(sd == Trend_Sinus_Noise)
     {
      st = "Trend + Sinus + Noise";
     }
   if(sd == RandomWalk)
     {
      st = "Random Walk";
     }
   if(sd == WhiteNoise)
     {
      st = "White Noise ";
     }

   if(n_graph==1) // график данных
     {
      CCurve *curve = graphic.CurveAdd(data,ColorToARGB(clrRed,255),CURVE_LINES,st);
      graphic.XAxis().Name("Series " + st);
      graphic.BackgroundMain(st);
     }
   if(n_graph==2) // график сингулярных значений (relative_variance = sigma_i^2/Sum Sigma_j^2)
     {
      CCurve *curve = graphic.CurveAdd(data,ColorToARGB(clrBlue,255),CURVE_LINES,st);
      graphic.XAxis().Name("Index ");
      graphic.YAxis().Name("Singular values ");
      graphic.BackgroundMain("Singular values " + st);
     }
   graphic.XAxis().NameSize(18);
   graphic.YAxis().NameSize(18);
   graphic.BackgroundMainColor(ColorToARGB(clrBlack,255));
   graphic.BackgroundMainSize(24);
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(sec*1000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
   ChartRedraw(0);
  }

//+------------------------------------------------------------------+
//| Plot Graphic                                                     |
//+------------------------------------------------------------------+
void PlotGraphic(double &data1[],double &data2[], int sec,int n_graph)
  {
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   ulong width = ChartGetInteger(0,CHART_WIDTH_IN_PIXELS);
   ulong height = ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS);

   if(ObjectFind(0,"Graphic")<0)
      graphic.Create(0,"Graphic",0,0,0,int(width),int(height));
   else
      graphic.Attach(0,"Graphic");

   if(n_graph==3)
     {
      CCurve *curve =  graphic.CurveAdd(data1,ColorToARGB(clrRed,255),CURVE_LINES,"first");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrBlue,255),CURVE_LINES,"second");
      graphic.XAxis().Name(" ");
      graphic.BackgroundMain("first and second singular vectors");
     }
   if(n_graph==4) // scatter plot of singular vectors
     {
      CCurve *curve =  graphic.CurveAdd(data1,data2,ColorToARGB(clrRed,255),CURVE_LINES,"first");
      graphic.XAxis().Name("first singular vector");
      graphic.YAxis().Name("second singular vector");
      graphic.BackgroundMain("Scatter plot of singular vectors U_1 vs U_2");
     }

   if(n_graph==5) // график данных плюс прогноз
     {
      CCurve *curve = graphic.CurveAdd(data1,ColorToARGB(clrBlue,255),CURVE_LINES,"original");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrRed,255),CURVE_POINTS_AND_LINES,"reconstructed");
      graphic.XAxis().Name("Time ");
      graphic.YAxis().Name("Value ");
      graphic.BackgroundMain("Original(Blue) + reconstructed(Red) + forecast(Red) ");
      curve1.PointsSize(3);
     }

// график сравнения прогноза функции MQL5 SingularSpectrumAnalysisForecast с прогнозом Basic-SSA
   if(n_graph==6)
     {
      CCurve *curve = graphic.CurveAdd(data1,ColorToARGB(clrBlue,255),CURVE_LINES,"BasicSSA");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrRed,255),CURVE_LINES,"MQL5");
      graphic.XAxis().Name("reconstructed + forecast ");
      graphic.BackgroundMain(" MQL5 SingularSpectrumAnalysisForecast vs script Basic-SSA ");
      curve1.PointsSize(3);
     }
   graphic.XAxis().NameSize(18);
   graphic.YAxis().NameSize(18);
   graphic.BackgroundMainColor(ColorToARGB(clrBlack,255));
   graphic.BackgroundMainSize(24);
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(sec*1000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
   ChartRedraw(0);
  }

//+------------------------------------------------------------------+
//| Копируем вектор в массив                                         |
//+------------------------------------------------------------------+
void VectortoArray(vector &v, double &array[])
  {
   int v_size = (int)v.Size();
   ArrayResize(array,v_size);
   for(int i=0; i<v_size; i++)
     {
      array[i]   =  v[i];
     }
  }
//+------------------------------------------------------------------+
//| Траекторная матрица X                                            |
//+------------------------------------------------------------------+
void trajectory_matrix(vector & series,int window_length, matrix & X)
  {
   int N_ = (int)series.Size();
   int L_ = window_length;
   int K = N_ - L_ + 1;
   X=matrix::Zeros(L_,K);
   for(int i=0; i <L_;  i++)
     {
      for(int j=0; j <K;  j++)
        {
         X[i,j] = series[i+j];
        }
     }
  }
//+-------------------------------------------------------------------+
//| Диагональное усреднение матрицы                                   |
//| Вход: Xi - матрица L x K (элементарная матрица i-ой компоненты)   |
//| Выход: x_tilde - восстановленный временной ряд                    |
//+-------------------------------------------------------------------+
void diagonal_averaging(matrix &Xi,vector &x_tilde)
  {
   int L_ = (int)Xi.Rows();
   int K  = (int)Xi.Cols();
   int N_ = L_ + K - 1; // Длина исходного временного ряда

   x_tilde = vector::Zeros(N_);
   double total; // Сумма элементов на антидиагонали
   int w_n;      // Количество элементов на антидиагонали
   int k;
   for(int n=0; n < N_; n++)
     {
      total = 0;
      w_n = 0;
      for(int j=0; j <L_; j++)
        {
         k = n - j ; // Индекс столбца: n = j + k ---> k = n - j
         if(k >= 0 && k < K) // Проверка, что индекс в пределах матрицы
           {
            total = total + Xi[j, k];
            w_n = w_n + 1;
           }
        }
      x_tilde[n] = total / w_n; // Усреднение
     }
  }
//+------------------------------------------------------------------+

Заключение

В данной статье мы рассмотрели основы сингулярного спектрального анализа (SSA), метода, который использует сингулярное разложение (SVD) траекторной матрицы для выявления скрытых структур в данных. Мы показали, как SSA эффективно разделяет временной ряд на интерпретируемые компоненты — тренд, сезонность и шум, — обеспечивая их реконструкцию и прогнозирование.

Однако, метод имеет ограничения, в частности, неспособность надежно различать детерминированный и стохастический тренды, такие как случайное гауссовское блуждание. В то же время, стоит отметить, что SSA не ставит перед собой задачу строгой статистической классификации трендов — его сила в гибком разложении и выделении структуры данных, с чем он успешно справляется.

Применение SSA не ограничивается анализом одномерных временных рядов. Метод позволяет работать с многомерными данными, на его основе можно строить индикатор разладки (change-point detection) для обнаружения резких изменений в поведении финансовых инструментов. Эти направления представляют перспективу для будущих исследований, так как точное понимание природы данных критически важно для поиска рыночных закономерностей.