
Алгоритм хаотической оптимизации — Chaos optimization algorithm (COA)
Содержание
Введение
В современных вычислительных задачах, особенно в сфере финансовых рынков и алгоритмической торговли, эффективные методы оптимизации играют решающую роль. Среди множества алгоритмов глобальной оптимизации, особое место занимают подходы, вдохновленные природными явлениями. Алгоритм хаотической оптимизации (Chaos Optimization Algorithm, COA) представляет собой одно из таких инновационных решений, объединяющее теорию хаоса и методы глобальной оптимизации.
В данной статье я представлю усовершенствованный алгоритм хаотической оптимизации, который опирается на фундаментальные свойства хаотических систем — эргодичность, чувствительность к начальным условиям и квази-стохастическое поведение. Алгоритм использует различные хаотические отображения для эффективного исследования пространства поиска и попытки ухода от локальных оптимумов —проблемы, часто возникающей в методах оптимизации.
Особенность представленного алгоритма заключается в комбинировании хаотического поиска с методом взвешенного градиентного направления и адаптивными механизмами, позволяющими динамически регулировать параметры поиска. Благодаря использованию нескольких типов хаотических отображений — логистического, синусоидального и тент-отображения, алгоритм демонстрирует неплохую устойчивость к стагнации и способность находить глобальные оптимумы в сложных многоэкстремальных функциях. Собственно, как обычно, разберем весь алгоритм, затем протестируем его возможности на наших, уже ставших стандартными, тестовых функциях.
Реализация алгоритма
Алгоритм состоит из трех основных фаз:
- хаотического поиска с первой несущей волной, где начальные переменные хаоса инициализируются, далее генерируются последовательные значения хаотических переменных через логистическое отображение, и переменные хаоса отображаются на диапазон оптимизируемых переменных, причем, запоминается лучшее найденное решение;
- поиска вдоль направления взвешенного градиента;
- хаотического поиска со второй несущей волной, где осуществляется локальный поиск вокруг лучшего решения, при фрактальном подходе реализации размера шага.
На картинке ниже я постарался отобразить суть работы алгоритма хаотической оптимизации, главная идея которого — использование хаоса как полезного инструмента оптимизации, а не случайного процесса. Глобальный оптимум (яркое жёлтое свечение в центре) — это цель, которую мы хотим найти. Синие светящиеся частицы — это агенты поиска, которые движутся по хаотическим траекториям, данные траектории показаны светящимися линиями, демонстрирующими нелинейный характер движения.
Демонстрация ключевых свойств хаотического поведения: детерминированность (траектории плавные, а не случайные), эргодичность (частицы исследуют всё пространство), чувствительность к начальным условиям (разные частицы движутся по разным траекториям), при этом, динамика поиска отображает свечение разной интенсивности, показывая "энергию" поиска в разных областях, где концентрические круги вокруг оптимума символизируют области притяжения, размытие и градиенты передают непрерывность пространства поиска. Основные этапы алгоритма:
- широкий поиск вдали от центра (дальние частицы),
- постепенное приближение к перспективным зонам (средние траектории),
- локальный поиск вблизи оптимума (близкие к центру частицы).
В итоге получился своего рода "портрет" хаотической оптимизации, где хаос представлен не как беспорядок, а как управляемый процесс исследования пространства решений.

Рисунок 1. Визуализация хаотической оптимизации
Визуальная схема алгоритма, представленная ниже, отражает три основных этапа:
- First Carrier Wave Search (синий блок) использует хаотическое отображение для глобального поиска и преобразует хаотические переменные в пространство поиска,
- Weighted Gradient Search (оранжевый блок) — взвешенный градиентный метод, включает обработку ограничений через весовые коэффициенты,
- Second Carrier Wave Search (фиолетовый блок) — локальный поиск вокруг лучшего решения и адаптивная настройка параметра α.
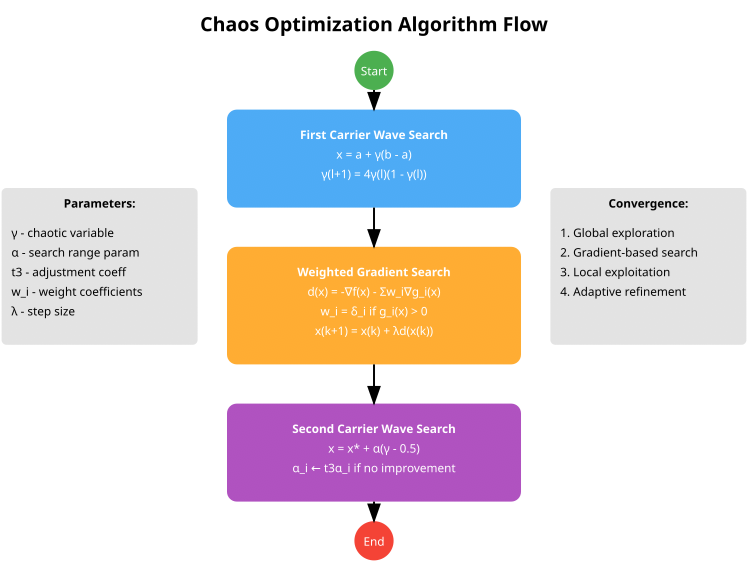
Рисунок 2. Схема работы алгоритма хаотической оптимизации
Схема представляет базовую трехэтапную структуру алгоритма COA (CHAOS). В моей реализации, а было их несколько, я решил остановиться на более продвинутой и практической версии алгоритма, расширил структуру агента, добавил счетчик перемещения, счетчик стагнации и хаотические переменные для каждого измерения. Немаловажным стало также добавление разнообразия для хаотических отображений, авторы базировались только на логистическом, в моей же версии добавлено синусоидальное и тент-отображение. Данная реализация включает автоматическую адаптацию параметров штрафа, адаптацию параметров поиска, в зависимости от успешности с регулировкой инерции. Кроме того, была добавлена более сложная инициализация с использованием латинского гиперкуба.
Приступим к написанию псевдокода алгоритма:
Инициализация алгоритма
- Установка параметров алгоритма:
- размер популяции (popSize)
- количество итераций первой фазы (S1)
- количество итераций второй фазы (S2)
- параметр штрафа (sigma)
- коэффициент корректировки (t3)
- малая константа для весовых коэффициентов (eps)
- параметр инерции (inertia)
- параметр социального влияния (socialFactor)
- вероятность мутации (mutationRate)
- Инициализация агентов:
- Для каждого агента в популяции:
- инициализировать хаотические переменные (gamma) с разными начальными значениями
- обнулить векторы скорости (velocity)
- установить счетчик стагнации в 0
- Для каждого агента в популяции:
- Инициализация параметров поиска (alpha):
- адаптировать параметры в зависимости от размера пространства поиска
- alpha[c] = 0.1 * (rangeMax[c] - rangeMin[c]) / sqrt(coords)
Фаза 1: Начальная популяция с хаотическим распределением
- Создание начальной популяции с использованием латинского гиперкуба:
- генерировать значения для каждого измерения
- перемешать значения для обеспечения равномерного распределения
- отобразить значения на диапазон переменных
- Применение разнообразных стратегий инициализации агентов:
- для первой четверти агентов: равномерное распределение
- для второй четверти: кластеризация вокруг нескольких точек
- для третьей четверти: случайные позиции со смещением к границам
- для последней четверти: хаотические позиции с разными отображениями
Фаза 2: Хаотический поиск с первой несущей волной
- Для каждой итерации до S1:
- Для каждого агента в популяции:
- если вероятность мутации сработала, применить мутацию
- иначе, для каждой координаты:
- обновить хаотическую переменную через выбранное отображение (логистическое, синусоидальное или тент)
- определить стратегию (глобальный или локальный поиск) на основе фазы оптимизации
- для глобального поиска: использовать хаотические значения для определения новой позиции
- для локального поиска: комбинировать притяжение к лучшим решениям с хаотическим возмущением
- обновить скорость с учетом инерции
- применить ограничения по скорости и позиции
- проверить нарушения ограничений и применить коррекцию
- Оценка и обновление:
- вычислить штрафную функцию для каждого агента
- обновить лучшие личные и глобальное решения
- динамически обновить параметр штрафа
- адаптировать параметр поиска (alpha) на основе успешности
- Для каждого агента в популяции:
Фаза 3: Хаотический поиск со второй несущей волной
- Для каждой итерации от S1 до S1+S2:
- проверить наличие сходимости
- для каждого агента в популяции:
- если обнаружена сходимость, применить случайную мутацию к некоторым агентам
- иначе, для каждой координаты:
- обновить хаотическую переменную
- адаптивно сузить радиус поиска
- выбрать базовую точку с приоритетом лучших решений
- добавить хаотическое возмущение и шум Леви для случайных дальних прыжков
- обновить скорость и позицию с инерцией
- применить ограничения по позиции
- Оценка и обновление:
- вычислить штрафную функцию для каждого агента
- обновить лучшие личные и глобальное решения
- обновить историю глобального лучшего решения для определения сходимости
- сбросить застрявшие агенты при необходимости
Вспомогательные функции
- Хаотические отображения:
- LogisticMap(x): x[n+1] = rx[n](1-x[n]) с проверкой корректности
- SineMap(x): x[n+1] = sin(π*x[n]) с нормализацией
- TentMap(x): x[n+1] = μ*min(x[n], 1-x[n]) с проверкой корректности
- SelectChaosMap(x, type): выбор отображения на основе типа
- Обработка ограничений и штрафов:
- CalculateConstraintValue(agent, coord): вычисление нарушения ограничений
- CalculateConstraintGradient(agent, coord): вычисление градиента ограничений
- CalculateWeightedGradient(agent, coord): вычисление взвешенного градиента
- CalculatePenaltyFunction(agent): вычисление значения штрафной функции
- Обработка стагнации и сходимости:
- IsConverged(): проверка сходимости на основе истории лучших решений
- ResetStagnatingAgents(): сброс агентов, находящихся в стагнации
- ApplyMutation(agent): применение различных типов мутаций
- UpdateSigma(): динамическое обновление параметра штрафа
- UpdateBestHistory(newBest): обновление истории лучших значений
Теперь можем переходить к описанию реализации алгоритма COA (CHAOS). В этой статье разберем все ключевые методы реализации, а в следующей — перейдем непосредственно к тестированию и результатам работы алгоритма. Напишем структуру "S_COA_Agent", поля структуры:
- gamma [] — набор хаотических переменных типа псевдослучайных, используется для внесения элементов случайности и разнообразия в поведение агента,
- velocity [] — массив скоростей, позволяет агенту более динамично перемещаться по пространству, учитывая инерцию,
- stagnationCounter — счётчик, который увеличивается, если агент не показывает улучшений в решении, помогает реализовать механизмы перезапуска стратегий при застоях.
В методе "Init ()" создаются и задаются начальные значения массивов. Для "gamma []" используется равномерное распределение от 0.1 до 0.9, чтобы внести разнообразие в начальные условия хаотических переменных. Скорости "velocity []" начинаются с нулевых значений, счётчик стагнации устанавливается в ноль.
//—————————————————————————————————————————————————————————————————————————————— // Улучшенная структура агента с дополнительными полями struct S_COA_Agent { double gamma []; // хаотические переменные double velocity []; // скорость перемещения (для усиления инерции) int stagnationCounter; // счётчик стагнации void Init (int coords) { ArrayResize (gamma, coords); ArrayResize (velocity, coords); // Равномерное распределение значений для gamma for (int i = 0; i < coords; i++) { // Используем различные начальные значения для лучшего разнообразия gamma [i] = 0.1 + 0.8 * (i % coords) / (double)MathMax (1, coords - 1); // Инициализация скорости нулями velocity [i] = 0.0; } stagnationCounter = 0; } }; //——————————————————————————————————————————————————————————————————————————————
Класс "C_AO_COA_chaos" является производным от базового класса "C_AO" и представляет собой реализацию алгоритма COA(CHAOS). Он включает в себя методы и параметры, необходимые для работы, а также дополнительные функции для управления поведением агентов, основываясь на концепциях хаотического поиска. Компоненты класса:
- SetParams () — метод для установки параметров алгоритма,
- Init () — метод инициализации, принимает диапазоны и параметры для работы алгоритма,
- Moving () — метод, отвечающий за перемещение агентов в пространстве решения,
- Revision () — метод для пересмотра положений агентов.
- S1, S2 — количество итераций в двух фазах алгоритма.
- sigma, t3, eps, inertia, socialFactor, mutationRate — параметры, влияющие на поведение агентов и алгоритм в целом.
- alpha [] — массив параметров, используемых для поиска.
- agent [] — массив агентов, составляющих популяцию алгоритма.
- методы для вычисления градиентов, значений ограничений и штрафных функций, а также проверки допустимости решений (IsFeasible),
- методы для хаотических отображений (LogisticMap, SineMap, TentMap, SelectChaosMap).
- переменные, хранящие информацию о текущей эпохе (epochs, epochNow), и динамическое значение штрафа (currentSigma),
- globalBestHistory [] — массив для хранения глобально лучших значений за несколько итераций,
- Индекс истории (historyIndex) для отслеживания позиции в массиве наилучших значений,
- Методы для управления популяцией агентов (InitialPopulation), выполнения различных фаз поиска (FirstCarrierWaveSearch, SecondCarrierWaveSearch), мутации агентов (ApplyMutation), обновления штрафа (UpdateSigma), и проверки сходимости (IsConverged), а также сброса застоявшихся агентов (ResetStagnatingAgents).
Итак, класс "C_AO_COA_chaos" представляет собой сложный компонент системы оптимизации, использующий агентов для поиска решений. Он интегрирует параметры, методы и логику, необходимые для управления агентами в рамках алгоритма, включая как детерминированные, так и хаотические стратегии.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_COA_chaos : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_COA_chaos () { } C_AO_COA_chaos () { ao_name = "COA(CHAOS)"; ao_desc = "Chaos Optimization Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16729"; // Внутренние параметры (не настраиваются извне) inertia = 0.7; socialFactor = 1.5; mutationRate = 0.05; // Параметры по умолчанию popSize = 50; S1 = 30; S2 = 20; sigma = 2.0; t3 = 1.2; eps = 0.0001; // Инициализация массива параметров для интерфейса C_AO ArrayResize (params, 6); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "S1"; params [1].val = S1; params [2].name = "S2"; params [2].val = S2; params [3].name = "sigma"; params [3].val = sigma; params [4].name = "t3"; params [4].val = t3; params [5].name = "eps"; params [5].val = eps; } void SetParams () { // Обновление внутренних параметров из массива params popSize = (int)params [0].val; S1 = (int)params [1].val; S2 = (int)params [2].val; sigma = params [3].val; t3 = params [4].val; eps = params [5].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- // Внешние параметры алгоритма int S1; // итерации первой фазы int S2; // итерации второй фазы double sigma; // параметр штрафа double t3; // коэффициент корректировки alpha double eps; // малое число для весовых коэффициентов // Внутренние параметры алгоритма double inertia; // параметр инерции для движения (внутренний) double socialFactor; // параметр социального влияния (внутренний) double mutationRate; // вероятность мутации (внутренний) S_COA_Agent agent []; // массив агентов private: //------------------------------------------------------------------- int epochNow; double currentSigma; // Динамический параметр штрафа double alpha []; // параметры поиска double globalBestHistory [10]; // История значений глобального лучшего решения int historyIndex; // Вспомогательные методы double CalculateWeightedGradient (int agentIdx, int coordIdx); double CalculateConstraintValue (int agentIdx, int coordIdx); double CalculateConstraintGradient (int agentIdx, int coordIdx); double CalculatePenaltyFunction (int agentIdx); // Метод для проверки допустимости решения bool IsFeasible (int agentIdx); // Хаотические отображения double LogisticMap (double x); double SineMap (double x); double TentMap (double x); double SelectChaosMap (double x, int type); void InitialPopulation (); void FirstCarrierWaveSearch (); void SecondCarrierWaveSearch (); void ApplyMutation (int agentIdx); void UpdateSigma (); void UpdateBestHistory (double newBest); bool IsConverged (); void ResetStagnatingAgents (); }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_COA" отвечает за начальную настройку и подготовку алгоритма к работе. Он выполняет несколько важных задач: первым делом выполняется базовая инициализация с помощью метода "StandardInit ()", которая устанавливает диапазоны, шаги и другие параметры. Если она не проходит успешно, метод завершается с ошибкой.
Далее устанавливаются параметры, связанные с количеством эпох (epochs), текущей эпохой (epochNow), а также коэффициентом штрафа (currentSigma). Инициализируется история лучших решений, которая помогает отслеживать прогресс. Проверяется размер массивов диапазонов минимальных и максимальных значений для поиска. Если размеры не совпадают или не заданы, инициализация прерывается.
Далее инициализируются массивы, в которых хранятся агенты, коэффициенты "alpha", а так же лучшие найденные решения. Каждый агент получает начальную позицию с учетом различных стратегий:
- часть агентов располагаются равномерно по всему диапазону,
- другие "clustering" — вокруг нескольких точек внутри диапазона,
- еще часть позиционируется случайным образом с учетом границ,
- остальные используют хаотические отображающие функции для получения стартовых решений.
Метод инициализации "Init" класса "C_AO_COA_chaos" задаёт начальные параметры и массивы, необходимые для поиска оптимального решения. Процесс включает в себя проверку корректности входных данных, настройку диапазонов поиска, инициализацию массива агентов с разнообразными стратегиями стартовых позиций, а также установку значений глобальных переменных, таких как лучшее найденное решение. В ходе выполнения метода создаются структуры данных, необходимые для дальнейшего итерационного процесса оптимизации, и задаются параметры, регулирующие поведение агентов и алгоритма в целом.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochNow = 0; currentSigma = sigma; historyIndex = 0; // Инициализация истории лучших значений for (int i = 0; i < 10; i++) globalBestHistory [i] = -DBL_MAX; // Проверка и инициализация основных массивов int arraySize = ArraySize (rangeMinP); if (arraySize <= 0 || arraySize != ArraySize (rangeMaxP) || arraySize != ArraySize (rangeStepP)) { return false; } ArrayResize (agent, popSize); ArrayResize (alpha, coords); // Адаптивная инициализация alpha в зависимости от диапазона поиска for (int c = 0; c < coords; c++) { // alpha зависит от размера пространства поиска double range = rangeMax [c] - rangeMin [c]; alpha [c] = 0.1 * range / MathSqrt (MathMax (1.0, (double)coords)); } // Инициализация агентов с разнообразными стратегиями for (int i = 0; i < popSize; i++) { agent [i].Init (coords); for (int c = 0; c < coords; c++) { double position; // Различные стратегии инициализации if (i < popSize / 4) { // Равномерное распределение по пространству position = rangeMin [c] + (i * (rangeMax [c] - rangeMin [c])) / MathMax (1, popSize / 4); } else if (i < popSize / 2) { // Кластеризация вокруг нескольких точек int cluster = (i - popSize / 4) % 3; double clusterCenter = rangeMin [c] + (cluster + 1) * (rangeMax [c] - rangeMin [c]) / 4.0; position = clusterCenter + u.RNDfromCI (-0.1, 0.1) * (rangeMax [c] - rangeMin [c]); } else if (i < 3 * popSize / 4) { // Случайные позиции с смещением в сторону границ double r = u.RNDprobab (); if (r < 0.5) position = rangeMin [c] + 0.2 * r * (rangeMax [c] - rangeMin [c]); else position = rangeMax [c] - 0.2 * (1.0 - r) * (rangeMax [c] - rangeMin [c]); } else { // Хаотические позиции с использованием разных отображений int mapType = i % 3; double chaosValue = SelectChaosMap (agent [i].gamma [c], mapType); position = rangeMin [c] + chaosValue * (rangeMax [c] - rangeMin [c]); } a [i].cB [c] = u.SeInDiSp (position, rangeMin [c], rangeMax [c], rangeStep [c]); } } return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "LogisticMap" реализует логистическое отображение, которое используется для генерации хаотических последовательностей. Эта функция применяется в алгоритме для внесения случайности и разнообразия в поиск решений. Основная идея метода — вычислить новое значение состояния на основе текущего, используя формулу логистического отображения с параметром, который слегка варьируется для повышения извлекаемой хаотичности.
Перед вычислением, значение входных данных проверяется на корректность и диапазон; в случае несоответствия, оно заменяется случайным числом в заданном диапазоне. После вычисления нового значения также проводится проверка на допустимый диапазон, и, при необходимости, оно заменяется на случайное число для сохранения устойчивости функции. В результате, внутренняя логика обеспечивает генерацию следующего состояния, остающегося в допустимых пределах.
//—————————————————————————————————————————————————————————————————————————————— // Улучшенные хаотические отображения double C_AO_COA_chaos::LogisticMap (double x) { // Защита от некорректных входных значений if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false) { x = 0.2 + 0.6 * u.RNDprobab (); } // x(n+1) = r*x(n)*(1-x(n)) double r = 3.9 + 0.1 * u.RNDprobab (); // Слегка рандомизированный параметр для избежания циклов double result = r * x * (1.0 - x); // Дополнительная проверка корректности if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false) { result = 0.2 + 0.6 * u.RNDprobab (); } return result; } //——————————————————————————————————————————————————————————————————————————————
Метод "SineMap" реализует хаотическое отображение, основанное на функции синуса. Он принимает текущее состояние, проверяет его корректность, и если оно некорректно или выходит за диапазон [0, 1], заменяет его случайным значением в этом диапазоне. Затем вычисляет новое значение с помощью функции синуса, нормализует его так, чтобы оно снова находилось в диапазоне [0, 1], и выполняет дополнительную проверку.
Если конечное значение выходит за границы или является недопустимым, оно снова заменяется случайным числом в диапазоне [0.2, 0.8]. В результате, метод возвращает новое состояние, которое получается на основе текущего с помощью хаотического отображения.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::SineMap (double x) { // Защита от некорректных входных значений if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false) { x = 0.2 + 0.6 * u.RNDprobab (); } // x(n+1) = sin(π*x(n)) double result = MathSin (M_PI * x); // Нормализация результата к диапазону [0, 1] result = (result + 1.0) / 2.0; // Дополнительная проверка корректности if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false) { result = 0.2 + 0.6 * u.RNDprobab (); } return result; } //——————————————————————————————————————————————————————————————————————————————
Метод "TentMap" реализует отображение "палатка" (tent map) для генерации хаотической последовательности. Метод берет входное значение "x", которое должно быть между 0 и 1 и проверяет "x" на корректность и, при необходимости, заменяет случайным значением в допустимом диапазоне. Далее, с использованием параметра "mu", близкого к 2, вычисляется новое значение на основе кусочно-линейной функции, характерной для отображения "палатка".
После вычисления, проводится еще одна проверка на допустимость значения, и, в случае необходимости, оно нормализуется случайным числом. Затем метод возвращает новое, хаотически сгенерированное значение.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::TentMap (double x) { // Защита от некорректных входных значений if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false) { x = 0.2 + 0.6 * u.RNDprobab (); } // Tent map: x(n+1) = μ*min(x(n), 1-x(n)) double mu = 1.99; // Параметр близкий к 2 для хаотического поведения double result; if (x <= 0.5) result = mu * x; else result = mu * (1.0 - x); // Дополнительная проверка корректности if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false) { result = 0.2 + 0.6 * u.RNDprobab (); } return result; } //——————————————————————————————————————————————————————————————————————————————
Метод "SelectChaosMap" предназначен для выбора и применения хаотической отображающей функции в зависимости от заданного типа. Он принимает значение "x" и параметр "type", который указывает на конкретный вид хаотического отображения. Основная идея метода — использовать остаток от деления типа на 3 для определения варианта отображения, что обеспечивает циклический выбор между тремя разными хаотическими картами: логистической, синусоидальной и тентовой. В зависимости от результата, вызывается соответствующая функция, которая преобразует входное значение "x" в новое, с помощью выбранной хаотической динамики.
Если по каким-либо причинам тип не попадает в ожидаемый диапазон (0, 1, 2), по умолчанию применяется логистическая карта. Каждая из этих карт моделирует хаотическое поведение и используется для генерации разнообразных и непредсказуемых чисел в рамках процесса оптимизации.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::SelectChaosMap (double x, int type) { // Выбор хаотического отображения на основе типа switch (type % 3) { case 0: return LogisticMap (x); case 1: return SineMap (x); case 2: return TentMap (x); default: return LogisticMap (x); } } //——————————————————————————————————————————————————————————————————————————————
Метод "InitialPopulation" предназначен для инициализации начальной популяции алгоритма оптимизации с использованием техники "Latin Hypercube Sampling (LHS)". LHS — это стратифицированный метод выборки, который обеспечивает более равномерное покрытие многомерного пространства поиска по сравнению со случайной выборкой, тем самым повышая качество начальной популяции.
Метод начинает работать с объявления массивов для значений латинского гиперкуба и временных значений, которые помогут в генерации. Метод пытается выделить память для необходимых массивов, и, если выделение памяти не удается, происходит резервный сценарий, который создает начальную популяцию случайным образом. Это обеспечивает то, что программа не завершится с ошибкой из-за нехватки памяти.
Далее метод генерирует значения для латинского гиперкуба. Для каждой координаты создается упорядоченный массив значений, который затем перемешивается случайным образом. Перемешанные значения присваиваются массиву гиперкуба. Значения латинского гиперкуба преобразуются в координаты особей в пространстве поиска. Расчет производится с использованием заданных диапазонов, и полученные значения ограничиваются в нужном диапазоне и шаге.
В конце метод устанавливает флаг, указывающий на то, что начальная популяция была изменена или создана. Преимущество этого подхода заключается в создании более диверсифицированной начальной популяции.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::InitialPopulation () { // Создаем Latin Hypercube для начальной популяции double latinCube []; // Одномерный массив для хранения значений гиперкуба double tempValues []; // Временный массив для хранения и перемешивания значений ArrayResize (latinCube, popSize * coords); ArrayResize (tempValues, popSize); // Генерируем Латинский гиперкуб for (int c = 0; c < coords; c++) { // Создаем упорядоченные значения for (int i = 0; i < popSize; i++) { tempValues [i] = (double)i / popSize; } // Перемешиваем значения for (int i = popSize - 1; i > 0; i--) { int j = (int)(u.RNDprobab () * (i + 1)); if (j < popSize) { double temp = tempValues [i]; tempValues [i] = tempValues [j]; tempValues [j] = temp; } } // Присваиваем перемешанные значения for (int i = 0; i < popSize; i++) { latinCube [i * coords + c] = tempValues [i]; } } // Преобразуем значения Латинского гиперкуба в координаты for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double x = rangeMin [c] + latinCube [i * coords + c] * (rangeMax [c] - rangeMin [c]); a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "FirstCarrierWaveSearch" реализует этап поиска в алгоритме, направленный на балансировку между глобальным исследованием пространства и локальной эксплуатацией известных хороших решений. Его основная задача — обновить позиции и скорости агентов, продолжая находить и улучшать потенциальные решения. В начале метода определяется коэффициент, который управляет степенью исследования в текущей эпохе поиска. Этот коэффициент уменьшается квадратично, по мере прогресса эпох, что обеспечивает постепенное смещение акцента с глобальных поисковых операций на локальное совершенствование. Затем, для каждого агента в популяции, происходит проверка на мутацию — с некоторой вероятностью выполняется мутация для повышения разнообразия решений. После этого, для каждого направления поиска (координаты):
- выбирается тип хаотического отображения, который используется для появления новых потенциальных решений,
- определяется стратегия поиска: либо глобальный, либо локальный.
При глобальном поиске, агент обновляет свою позицию с помощью хаотического компонента, а скорость корректируется с учетом инерции и направления движения. В случае локального поиска, агент ориентируется на лучшие найденные решения, делая взвешенное притяжение к ним с небольшой случайной вариацией для предотвращения зацикливания. В обоих случаях скорость ограничивается, чтобы избежать слишком больших прыжков за границы поискового пространства. Позиции агентов обновляются с учетом ограничений пространства поиска, и, при необходимости, выполняется поправка, если обнаружены нарушения ограничений. В этом случае, позиции корректируются, а скорости уменьшаются, чтобы сгладить последующие шаги.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::FirstCarrierWaveSearch () { // Адаптивный баланс между исследованием и эксплуатацией double globalPhase = (double)epochNow / S1; double explorationRate = 1.0 - globalPhase * globalPhase; // Квадратичное снижение // Для каждого агента for (int i = 0; i < popSize; i++) { // Применяем мутации с некоторой вероятностью для усиления разнообразия if (u.RNDprobab () < mutationRate * (1.0 + explorationRate)) { ApplyMutation (i); continue; } for (int c = 0; c < coords; c++) { // Выбор хаотического отображения с равномерным распределением int mapType = ((i + c + epochNow) % 3); // Безопасная проверка доступа к массиву gamma if (c < ArraySize (agent [i].gamma)) { agent [i].gamma [c] = SelectChaosMap (agent [i].gamma [c], mapType); } else { continue; // Пропускаем, если индекс некорректен } // Определяем соотношение между глобальным и локальным поиском double strategy = u.RNDprobab (); double x; if (strategy < explorationRate) { // Глобальный поиск с хаотическим компонентом x = rangeMin [c] + agent [i].gamma [c] * (rangeMax [c] - rangeMin [c]); // Добавляем компонент скорости для сохранения направления движения agent [i].velocity [c] = inertia * agent [i].velocity [c] + (1.0 - inertia) * (x - a [i].c [c]); } else { // Локальный поиск вокруг лучших решений double personalAttraction = u.RNDprobab (); double globalAttraction = u.RNDprobab (); // Взвешенное притяжение к лучшим решениям double attractionTerm = //personalAttraction * (agent [i].cPrev [c] - a [i].c [c]) + personalAttraction * (a [i].cB [c] - a [i].c [c]) + socialFactor * globalAttraction * (cB [c] - a [i].c [c]); // Хаотическое возмущение для предотвращения застревания double chaosRange = alpha [c] * explorationRate; double chaosTerm = chaosRange * (2.0 * agent [i].gamma [c] - 1.0); // Обновление скорости с инерцией agent [i].velocity [c] = inertia * agent [i].velocity [c] + (1.0 - inertia) * (attractionTerm + chaosTerm); } // Ограничиваем скорость для предотвращения слишком больших шагов double maxVelocity = 0.1 * (rangeMax [c] - rangeMin [c]); if (MathAbs (agent [i].velocity [c]) > maxVelocity) { agent [i].velocity [c] = maxVelocity * (agent [i].velocity [c] > 0 ? 1.0 : -1.0); } // Применяем скорость к позиции x = a [i].c [c] + agent [i].velocity [c]; // Применяем ограничения поискового пространства a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); // Проверяем ограничения и применяем плавную коррекцию double violation = CalculateConstraintValue (i, c); if (violation > eps) { double gradient = CalculateWeightedGradient (i, c); double correction = -gradient * violation * (1.0 - globalPhase); a [i].c [c] = u.SeInDiSp (a [i].c [c] + correction, rangeMin [c], rangeMax [c], rangeStep [c]); // Сбрасываем скорость при коррекции нарушений agent [i].velocity [c] *= 0.5; } } } } //——————————————————————————————————————————————————————————————————————————————
Метод "SecondCarrierWaveSearch" представляет собой этап оптимизации, который развивается после начального поиска и ориентирован на углубление и уточнение найденных решений. Основная цель этого метода заключается в улучшении результатов, достигнутых в результате предшествующего этапа, путем применения более тонких стратегий поиска и адаптации параметров.
Метод начинает свою работу с вычисления параметра, отражающего фазу локального поиска, который со временем усиливается. Это позволяет алгоритму постепенно переходить от широкого поиска к более детализированному и точному исследованию области уже известных решений. В начале метода происходит проверка на достижение сходимости. Если алгоритм достиг стабильного состояния, некоторые агенты подвергаются мутации, для увеличения разнообразия решений и избегания местных экстремумов.
Для каждого агента осуществляется последовательный поиск новых решений в его пространстве. Определяются хаотические отображения, которые помогают внедрять элементы случайности. Параметр поиска уменьшается, по мере приближения к оптимальному решению. Это обеспечивает более узкий фокус при поиске вблизи текущих лучших решений. При обновлении каждой позиции учитываются прошлые достижения агентов. Определяется базовая точка, которая может быть как абсолютным глобальным оптимумом, так и предыдущими личными достижениями агента, что помогает учесть как индивидуальные, так и общие результаты всей популяции.
В процессе обновления позиций используется как хаотическое смещение, так и случайный шум (например, шум Леви), что добавляет элемент случайности и способствует поиску новых, потенциально лучших решений. Метод учитывает инерцию при обновлении скоростей агентов, это позволяет смягчить изменения и предотвратить агрессивные перемещения. В результате, обновленные позиции ограничиваются по заданным границам, что обеспечивает соблюдение условий задачи.
Метод "SecondCarrierWaveSearch" нацелен на более точную и глубокую оптимизацию уже имеющихся решений.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::SecondCarrierWaveSearch () { // Уточняющий локальный поиск с адаптивными параметрами double localPhase = (double)(epochNow - S1) / S2; double intensificationRate = localPhase * localPhase; // Квадратичное увеличение интенсификации // Проверка на сходимость алгоритма bool isConverged = IsConverged (); // Для каждого агента for (int i = 0; i < popSize; i++) { // Если обнаружена сходимость, добавляем случайную мутацию к некоторым агентам if (isConverged && i % 3 == 0) { ApplyMutation (i); continue; } for (int c = 0; c < coords; c++) { // Выбор хаотического отображения с равномерным распределением int mapType = ((i * c + epochNow) % 3); agent [i].gamma [c] = SelectChaosMap (agent [i].gamma [c], mapType); // Адаптивный радиус поиска с сужением к концу оптимизации double adaptiveAlpha = alpha [c] * (1.0 - 0.8 * intensificationRate); // Выбор базовой точки с приоритетом лучших решений double basePoint; if (a [i].f > a [i].fB) { basePoint = a [i].c [c]; // Текущее положение лучше } else { double r = u.RNDprobab (); if (r < 0.7 * (1.0 + intensificationRate)) // Увеличиваем притяжение к глобальному лучшему { basePoint = cB [c]; // Глобальное лучшее } else { basePoint = a [i].cB [c]; // Личное лучшее } } // Локальный поиск с хаотическим компонентом double chaosOffset = adaptiveAlpha * (2.0 * agent [i].gamma [c] - 1.0); // Добавляем шум Леви для случайных дальних прыжков (тяжелый хвост распределения) double levyNoise = 0.0; if (u.RNDprobab () < 0.1 * (1.0 - intensificationRate)) { // Упрощенное приближение шума Леви double u1 = u.RNDprobab (); double u2 = u.RNDprobab (); if (u2 > 0.01) // Защита от деления на очень малые числа { levyNoise = 0.01 * u1 / MathPow (u2, 0.5) * adaptiveAlpha * (rangeMax [c] - rangeMin [c]); } } // Обновляем скорость с инерцией agent [i].velocity [c] = inertia * (1.0 - 0.5 * intensificationRate) * agent [i].velocity [c] + (1.0 - inertia) * (chaosOffset + levyNoise); // Применяем скорость к позиции double x = basePoint + agent [i].velocity [c]; // Ограничиваем позицию a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
В следующей статье продолжим рассмотрение оставшихся методов работы алгоритма, проведем тестирование и подведем итоги.
 Нейросети в трейдинге: Оптимизация LSTM для целей прогнозирования многомерных временных рядов (Окончание)
Нейросети в трейдинге: Оптимизация LSTM для целей прогнозирования многомерных временных рядов (Окончание)
 HTTP и Connexus (Часть 2): Понимание архитектуры HTTP и дизайна библиотеки
HTTP и Connexus (Часть 2): Понимание архитектуры HTTP и дизайна библиотеки
 Создание самооптимизирующихся советников на языках MQL5 и Python (Часть II): Настройка глубоких нейронных сетей
Создание самооптимизирующихся советников на языках MQL5 и Python (Часть II): Настройка глубоких нейронных сетей
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
