Модифицированный советник Grid-Hedge в MQL5 (Часть III): Оптимизация простой хеджирующей стратегии (I)

Введение

Добро пожаловать в третью часть серии статьей о хеджирующих советниках. Начнем с краткого обзора прогресса нашей программы на сегодняшний день. На данный момент мы разработали два ключевых компонента: советник Simple Hedge и советник Simple Grid. В этой статье основное внимание мы уделим дальнейшему улучшению советника Simple Hedge. Наша цель — улучшить его работу за счет сочетания математического анализа и метода "грубой силы" (brute-force), чтобы найти наиболее эффективный способ реализации этой торговой стратегии.

В первую очередь речь пойдет о математической оптимизации стратегии Simple Hedge. Из-за сложности и глубины необходимого анализа нецелесообразно описывать в одной статье как математическую оптимизацию, так и последующую оптимизацию на основе кода. Поэтому мы посвятим эту статью математическим аспектам, чтобы максимально полно исследовать теорию и расчеты, лежащие в основе процесса оптимизации. В последующих статьях этой серии мы обсудим аспект оптимизации кода, применяя практические методы программирования к теоретическим основам, заложенным здесь.

В этой статье мы поговорим вот о чем:

1. Углубление оптимизации: более детальное обсуждение
2. Математическая оптимизация
3. Заключение

Углубление оптимизации: более детальное обсуждение

Что приходит на ум, когда мы произносим слово «оптимизация»? Это термин настолько же широкий, насколько и сложный. Так что же такое оптимизация?

Давайте разберемся. По своей сути оптимизация относится к действию, процессу или методологии доработки чего-либо — будь то дизайн, система или решение — до высшего уровня совершенства, функциональности или эффективности. Но давайте посмотрим правде в глаза: достижение абсолютного совершенства — это скорее идеалистическое стремление. Настоящая цель? Раздвигать границы возможного с имеющимися у нас ресурсами и стремиться к наилучшему результату.

Область оптимизации обширна, и в нашем распоряжении имеется множество методов. В контексте нашего обсуждения мы сосредоточим внимание на «классической стратегии хеджирования». Среди множества методов оптимизации краеугольным камнем нашего исследования станут два подхода:

1. Математическая оптимизация — этот подход использует всю мощь математики. Представьте себе, что вы можете создавать функции прибыли, функции просадки и многое другое, а затем использовать эти конструкции для точной настройки стратегии на основе надежных, поддающихся количественной оценке данных. Это метод, который не только повышает точность усилий по оптимизации, но и обеспечивает четкий математический путь к повышению эффективности стратегии.

2. Подход "грубой силы" — метод brute force простой, но впечатляющий по своим масштабам. Этот метод включает в себя тестирование каждой мыслимой комбинации входных данных с целью найти наилучшую возможную конфигурацию. В чем конечная цель такого подхода? Либо максимизировать прибыль, либо минимизировать просадки, в зависимости от стратегических приоритетов. Но важно отметить явный сложный момент — огромное количество комбинаций ввода. Эта сложность делает тестирование всех возможных сценариев на истории невообразимой задачей, особенно при ограниченных ресурсах и времени.
   

От чего мы можем выиграть, так это от объединения двух подходов. Применив сначала математическую оптимизацию, мы можем значительно сократить количество проходов для грубого перебора. Это стратегический маневр, который позволяет нам сосредоточиться на наиболее перспективных конфигурациях, сделает процесс грубой силы намного более управляемым и экономным.

По сути, путь оптимизации — это баланс между теоретической точностью и практической осуществимостью. Начиная с математической оптимизации, мы сможем отфильтровать множество вариантов. Затем переход к грубой силе позволит нам тщательно протестировать и уточнить оставшиеся варианты. Вместе эти методы образуют мощный дуэт для эффективной оптимизации нашей классической стратегии хеджирования.

Математическая оптимизация

Приступая к математической оптимизации, первым шагом нужно создать четкую и действенную структуру. Это означает определение переменных, которые оказывают влияние на результат — в данном случае на прибыль. Давайте проанализируем компоненты, которые играют решающую роль в формировании функции прибыли:

1. Initial Position (IP) — начальная позиция, бинарная переменная: 1 означает покупку, 0 — продажу. Первоначальный выбор закладывает основу для направления торговой стратегии.
2. Initial Lot Size (IL) — начальный лот, размер первого ордера в торговом цикле, закладывающая основу для масштабирования сделок.
3. Buy Take Profit (BTP) — тейк-профит для ордеров на покупку, определенный заранее порог для закрытия позиций и фиксации прибыли.
4. Sell Take Profit (STP) — аналогичный тейк-профит для сделок на продажу, определенный заранее порог для закрытия позиций на продажу и фиксации прибыли.
5. Buy-Sell Distance (D) — пространственный параметр, определяющий интервал между уровнями ордеров на покупку и продажу, влияющий на точки входа в сделки.
6. Lot Size Multiplier (M) — множитель лота увеличивает размер лота для последующих ордеров, вводя динамическую корректировку в зависимости от хода торгового цикла.
7. Number of Orders (N) — общее количество ордеров в цикле, отражающее широту торговой стратегии.

Для ясности эти параметры представлены в упрощенной форме, но в уравнениях некоторые из этих переменных будут обозначаться индексами.

Взяв эти параметры за основу, мы можем теперь приступить к формулированию функции прибыли. Суть этой функции состоит в том, чтобы математически представить, как изменение этих переменных влияет на нашу прибыль (или убыток). Функция прибыли является краеугольным камнем нашего процесса оптимизации, позволяя количественно анализировать результаты различных торговых стратегий в разных сценариях.

Запишем параметры нашей функции прибыли:

Таким образом, окончательная функция прибыли будет выглядеть так:

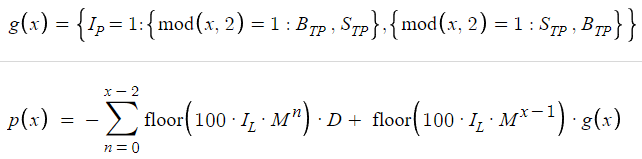
На первый взгляд функция прибыли может показаться сложной из-за ее математических выражений и символов. Однако не стоит пугаться. Каждый компонент уравнения играет определенную роль, которая позволяет понять, как генерируется прибыль в рамках нашей торговой системы.

Также нужно понять динамику расчета прибыли. Центральное место здесь занимает различие между основной функцией прибыли, обозначаемой p(x), и ее компонентом g(x), где x представляет собой общее количество ордеров или позиций. Это различие очень важно, поскольку позволяет понять, как генерируется прибыль, когда торговый цикл завершается на x позициях. Давайте разберем данную концепцию, чтобы полностью понять ее суть.

Предположим, мы решили закрыть торговый цикл одним ордером. В этом случае имеем такой сценарий:

Здесь g(x) принимает значение, основанное на взаимодействии количества ордеров (N) и начальной позиции (IP). Например, если мы установим начальный размер лота (IL) равным 0,01 и (для простоты пояснения) N равным 1, а начальную позицию (IP) установим на покупку (IP = 1), тогда g(x) примет значение Buy Take Profit (BTP). В результате наша функция прибыли p(x) становится 100 умноженной на 0,01 умноженной на BTP = BTP, что символически указывает на то, что наша прибыль равна BTP. Обратите внимание, что мы рассчитываем прибыль в пунктах, а не в валюте. Этот подход выбран намеренно, чтобы обобщить расчет прибыли для разных валют, обеспечить применимость независимо от типа счета (микро или стандартный) и упростить общий расчет. Здесь мы умножаем размера лота на 100, чтобы преобразовать размера лота в точное значение пункта, что позволяет точно рассчитать прибыль.

Теперь давайте рассмотрим случай, в котором N увеличивается до 2, т.е. введем новый уровень сложности:

 

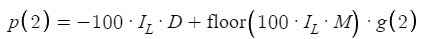
Эта небольшая корректировка усложняет расчет прибыли и требует более глубокого анализа основных причин, которые лучше всего иллюстрируются примерами. Критическим компонентом здесь является введение функции "floor", математической операции, напоминающей то, что мы знаем как наибольшую целочисленную функцию (GIF). Функция Floor служит определенной цели: учитывая любое числовое значение, она усекает десятичную составляющую до наибольшего предшествующего целого числа. Для положительных значений эта операция проста: Floor(1,54) = 1, Floor(4,52) = 4 и т.д. Этот механизм является неотъемлемой частью функции прибыли. Он гарантирует, что в расчетах учитываются только целочисленные значения. Это упрощение позволяет сосредоточиться на положительных значениях и избежать необходимости учитывать отрицательные значения в этом контексте.

Начальный сегмент формулы начинается с расчета минимального уровня как -100-кратного значения уровня воздействия Impact Level (IL), что иллюстрирует случай, когда IL равен 0,01. В результате получается расчет -100, умноженный на 0,01, что равно -1. При интеграции с расстоянием Distance (D), уравнение представляет потерю D пунктов для каждой сделки, которая не приводит к прибыли. Следующий шаг — добавить нижний предел, умноженный на 100 раз IL, умноженный на множитель (M), к функции g(x), которая представляет значение тейк-профита (TP) для ордера на покупку или продажу. Произведение IL и M определяет размер лота для последующего (второго) ордера, а умножение этого произведения на 100 облегчает точный расчет пунктов.

Ключевой вопрос возникает относительно необходимости использования функции Floor в нашем уравнении. Для пояснения рассмотрим пример, где IL равен 0,01, а M равен 2, в результате чего получается IL, умноженный на 100, умноженный на M, что равно 2. В этом случае применение функции Floor к 2 дает 2, что, по-видимому, делает эту функцию избыточной. Однако полезность функции floor становится очевидной в другом сценарии: если IL остается на уровне 0,01, а M установлено равным 1,5, произведение 100 раз IL на M будет равно 1,5. Полученный в итоге размер лота 0,015 недопустим, поскольку брокеры требуют, чтобы размеры лота были кратны 0,01. Согласно стратегии, размер ордера установится на 0,01, а последующие размеры лота будут контролируемо увеличиваться, чтобы гарантировать их работу в условиях требований брокера. Например, следующий размер лота, рассчитанный как 0,01×1,5×1,5, равен 0,0225, что фактически округляется до 0,02 для практических целей. Таким образом, функция нижнего предела floor используется для корректировки уравнения в соответствии с операционной реальностью, чтобы получить действенные размеры лотов: 0,01 и далее 0,02. Таким образом модель гарантированно соответствует практическим ограничениям торговли. Становится ясно, что нам необходимо использовать функцию Floor при расчете лотов. Наконец, скорректированное значение умножается на g(x), что соответствует либо TP покупки, либо TP продажи, что дополнительно вводит параметры торговой стратегии в формулу уравнения. Надеюсь это достаточное обоснование каждого компонента уравнения, описывающее стратегические соображения к его построению.

Теперь предположим, что N равно 3, тогда мы получим прибыль:

Когда N равно 3, формула иллюстрирует ситуацию, когда прибыль получается при определенных условиях, что приводит к структурированному подходу к расчету результатов на основе количества ордеров, обозначенного N. Первый сегмент представляет собой убыток по первому ордеру. Второй сегмент адаптирует подход, заменяя g(x) на D, что также отражает потери второго ордера. Различие в третьем сегменте связано с введением M^2, которое указывает на экспоненциальное увеличение множителя, учитывая контекст.

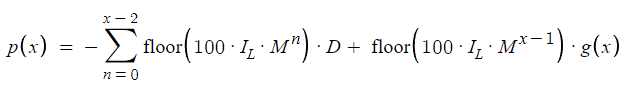
Как расширение структуры для различных значений N, представлено обобщенное уравнение, которое всесторонне отражает динамику этой торговой стратегии. Это уравнение, адаптируемое к различным случаям N, служит базовой моделью для понимания прогресса и потенциальных результатов по мере увеличения количества ордеров.

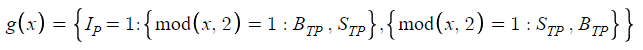
Определение g(x), которое попеременно происходит между тейк-профитом покупки (BTP) и тейк-профитом продажи (STP), зависит от начальной позиции (IP) и четности N. Этот процесс принятия двоичного решения отображается в условной структуре, где на результат влияют как IP, так и числовая характеристика N, а именно его четность или нечетность. Этот механизм обеспечивает логическое присвоение значений g(x) в соответствии с рыночной позицией и последовательностью ордеров.

Использование графического инструмента Desmos облегчает понимание этого уравнения, позволяя корректировать параметры в реальном времени благодаря немедленной обратной связи об изменениях. Способность этого инструмента отображать целочисленные результаты особенно ценна в практическом контексте, где количество ордеров по своей сути является дискретной переменной.

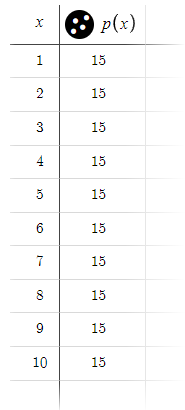
Демонстрация Desmos с предопределенными параметрами показывает поведение модели в стандартных условиях. По ней видно, что можно ожидать стабильной прибыли в 15 пунктов в диапазоне до 10 ордеров.

Примечание: для простоты мы пока игнорировали спреды.

Глядя на результаты, может возникнуть желание инвестировать в эту стратегию. Однако я хочу вас предостеречь от поспешных решений. Все еще есть много проблем, которые необходимо решить, прежде чем продолжить. Для более полного понимания ситуации было бы полезно ввести в нашу таблицу дополнительный столбец. Но перед этим давайте сформулируем и запишем уравнение, которое ляжет в основу этой новой колонки. Этот подготовительный шаг очень важен для анализа данных и позволяет лучше понять, как же происходит сам процесс принятия решений.

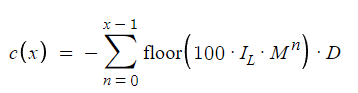
Уравнение иллюстрирует максимально возможную просадку. Если цикл заканчивается на 10-м ордере, максимальная просадка будет равна сумме, очень близкой к убытку, если бы 10-й ордер оказался убыточным. Это показано в уравнении, когда n меняется от 0 до x-1, тогда как ранее n менялось в диапазоне от 0 до x-2 для убытков перед прибылью.

Представленное уравнение определяет максимальную потенциальную просадку, показывая тем самым риски в этой стратегии. Например, предположим, что цикл завершается на 10-м ордере. В этом контексте максимальную просадку можно рассматривать как сумму, которая приблизительно соответствует возможному убытку в случае, если бы 10-й ордер привел к убытку. Расчет просадки включен в уравнении с помощью переменной n со значениями от 0 до x-1. В этом разделе указывается диапазон, используемый для расчета просадки. Это отход от предыдущего метода расчета убытков, который включал в себя прохождение n диапазона от 0 до x-2, за которым следовала прибыль. Такая корректировка параметров обеспечивает более точное представление профиля риска стратегии, потому что так мы учитываем максимально возможные потери до того, как будет реализована потенциальная прибыль.

Чтобы определить максимально возможную просадку с использованием входных параметров по умолчанию, смотрим, как значения новой переменной корректируются с изменениями x. Этот шаг позволят понять прямое влияние изменения х на потенциальную просадку, понять риск, связанный с различными сценариями в рамках нашей стратегии.

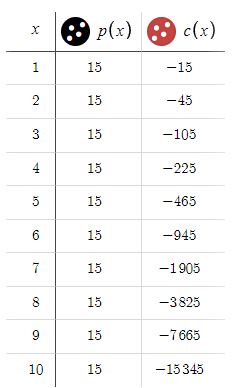
Учитывая, что мы завершаем цикл выигрышем по 10-му ордеру, мы ожидаем максимальную просадку в размере 15 345 долларов США. Эта цифра весьма существенна, особенно по сравнению с относительно скромным вознаграждением в размере 15 долларов США. Учитывая эту динамику, давайте увеличим параметры BTP и STP с 15 пунктов до 50 пунктов.

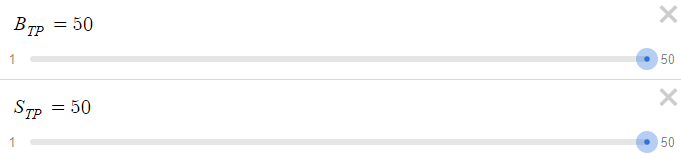
Теперь посмотрим на результат:

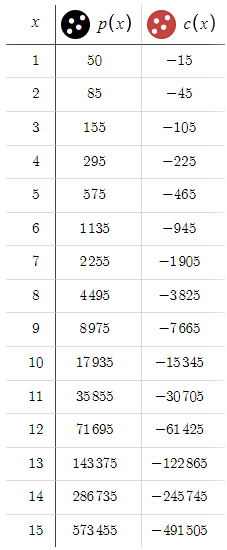
Здесь вы видите значительный отход от предыдущего сценария, в котором потери росли в геометрической прогрессии. Теперь мы находимся в положении, когда последовательно добиваемся прибыли и имеем при этом весьма благоприятное соотношение риска и прибыли. Учитывая такие обнадеживающие результаты, возникает вопрос: зачем ограничиваться целью в 50 пунктов? Давайте рассмотрим возможность расширения нашей цели до 100 пунктов.

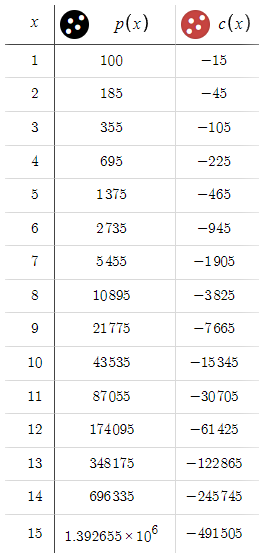
Обратите внимание, что значения c(x) остаются неизменными, в то время как p(x) увеличивается при всех значениях x. Это неравенство может заставить задуматься, учитывая значительное преимущество потенциальных прибылей над потерями. Однако здесь есть скрытая ловушка. Чтобы понять, представьте, что BTP и STP установлены, скажем, на уровне 10 000 пунктов. В таких обстоятельствах потребуется целая вечность, прежде чем цена достигнет этих целей. Это приводит нас к важному выводу: чем выше BTP и STP, тем ниже шансы на завершение цикла, т.е. достижение либо BTP, либо STP. Это вводит скрытый элемент, который мы назовем p — вероятность того, что цикл будет завершен при заданном x. Неоправданное увеличение BTP и STP снижает p, и чем ниже p, тем менее вероятно, что цикл будет завершен. Поэтому независимо от потенциальной прибыли, если p минимально, ожидаемая прибыль может никогда не материализоваться. Поскольку мы в основном имеем дело с EURUSD, где колебания в 100 пунктов уже значительны, будем использовать предварительный уровень в 50 пунктов как для BTP, так и для STP. Этот уровень основан на интуиции и может быть скорректирован по мере необходимости, чтобы эффективно сбалансировать риск и вознаграждение.

Учет p и расчет ожидаемой прибыли — сложная задача. Хотя математическая оптимизация обеспечивает структурированный подход, она сама по себе не может определить вероятность завершения цикла (p). Требуется анализ графиков для более детального понимания. Дальнейшие сложности возникают из-за того, что p по своей природе нестабильно и ведет себя как случайная величина. Важно понимать, что p представляет собой вектор значений вероятности, где каждый элемент указывает вероятность закрытия цикла после определенного количества общих ордеров. Например, первый элемент вектора представляет вероятность завершения цикла только с одним ордером, и эта логика распространяется на другие элементы для разных сумм ордеров. Всестороннее изучение этой концепции, особенно ее применения и последствий, будет ключевым моментом при переходе к оптимизации на основе кода в следующей статье этой серии.

В нашем анализе мы упустили из виду важный фактор: спред. Спред играет ключевую роль в нашей стратегии (как и во всех), он влияет как на прибыль, так и на убытки. Чтобы учесть его, мы корректируем наши расчеты, вычитая определенные значения из p(x) и c(x). Так добавим разброс в наш анализ.

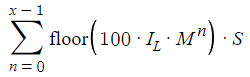
Важно отметить, что наша корректировка учитывает все сделки от нуля до x-1 — спред влияет на каждую сделку, независимо от того, прибыльна она или нет. Для простоты в настоящее время мы рассматриваем спред (обозначенный как S) как постоянное значение. Это решение принято, чтобы не усложнять математический анализ дополнительной изменчивой величиной. Хотя это упрощение ограничивает реалистичность модели, оно позволяет сосредоточиться на основных аспектах стратегии, не увязая в чрезмерной сложности.

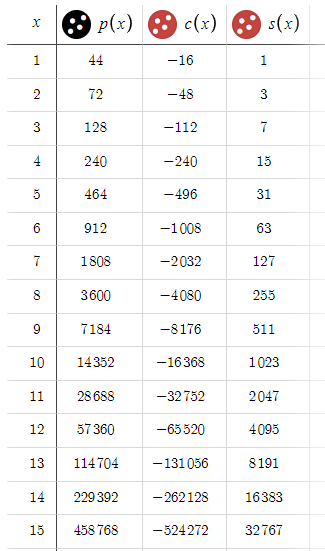
После введения в расчеты s(x) нужно количественно оценить реальное влияние спреда на нашу прибыль. Эффект весьма значителен: потери, связанные со спредом, возрастают по мере увеличения x и потенциально достигают 32 000 пунктов, или около 3200 долларов. Эта корректировка не только уменьшает нашу потенциальную прибыль на s(x), но и увеличивает наши потенциальные потери на ту же величину, значительно изменяя соотношение риска и прибыли. Этот сдвиг подчеркивает важность учета спреда при стратегическом планировании и необходимость тщательного управления этим фактором при оптимизации стратегии.

Переходя к последней задаче, когда мы говорим о сокращении вариантов для применения грубого перебора, мы имеем в виду процесс выборочного исключения определенных комбинаций параметров, которые вряд ли дадут полезные результаты для нашей стратегии. Этот шаг имеет решающее значение для оптимизации нашего подхода, особенно при подготовке к оптимизации в коде, поскольку позволяет сосредоточить вычислительные ресурсы на исследовании наиболее перспективных конфигураций.

Для примера давайте рассмотрим сценарий, в котором мы установили параметры BTP (триггерная точка покупки), STP (триггерная точка продажи) и D (расстояние) на 15, а M (множитель) на 1,5.

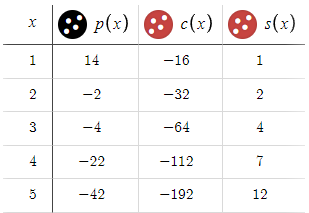
При анализе таких настроек можно быстро понять, что такие параметры дают неудовлетворительные результаты. Поэтому очевидно, что включение именно этих значений в стратегию или дальнейшие усилия по оптимизации будет бесполезным.

В связи с этим возникает вопрос: как заранее выявить и устранить такие неэффективные комбинации параметров? Хотя первоначальное открытие этих параметров было случайным, систематически выявлять и устранять все неоптимальные входные параметры довольно сложно. Это требует методического подхода, возможно, предварительный анализ для оценки возможности использования различных наборов параметров, прежде чем можно будет приступить к полномасштабной оптимизации методом грубой силы. Таким образом, мы можем упростить процесс оптимизации и гарантировать, что все усилия будут направлены только на те комбинации параметров, которые могут повысить эффективность нашей торговой стратегии.

Решение проблемы систематического выявления и устранения неоптимальных комбинаций параметров в нашем процессе оптимизации — сложная задача, которую мы решим в последующих частях этой серии. Такой подход обеспечит целенаправленное и эффективное исследование наиболее перспективных стратегий и тем самым повысит общую эффективность нашей торговой методологии. На этом остановимся. Далее продолжим в следующей части.

Заключение

В этой третьей части нашей серии мы перешли к более глубокому исследованию оптимизации стратегии Simple Hedge. Удили особое внимание математическому анализу, получили базовое представление о подходе "грубой силы", который будем использовать в следующей части.

Забегая вперед, скажу, что в следующих статьях этой серии мы перейдем от теоретических исследований к практической оптимизации на основе кода. Изученные принципы и идеи будем применять к реальным торговым сценариям. Этот сдвиг обещает сделать стратегию более четкой, предлагая ощутимые улучшения и действенные стратегии для трейдеров, стремящихся максимизировать прибыль при эффективном управлении рисками.

Я очень ценю все ваши комментарии и отзывы, которые вы оставили к предыдущим статьям из этой серии. Продолжайте делиться своими мыслями и предложениями. Вместе мы не просто оптимизируем торговую стратегию; мы прокладываем путь к более эффективным торговым решениям, которые смогут выдержать испытание волатильностью и неопределенностью рынка.

Удачного программирования! Удачной торговли!