Машинное обучение и Data Science (Часть 21): Сравниваем алгоритмы оптимизации в нейронных сетях
553
3
«Я не утверждаю, что нейронные сети — это просто. Нужно быть экспертом, чтобы заставить их работать. Но у этого опыта гораздо более широкое применение. Те усилия, которые раньше уходили на разработку функций, теперь направлены на разработку архитектуры, функции потерь и схемы оптимизации. Ручной труд переходит на более высокий уровень абстракции».
Стефано Соатто
Введение
Кажется, сегодня все интересуются искусственным интеллектом. Он повсюду, и крупные игроки в технологической индустрии, такие как Google и Microsoft, стоящие за openAI, продвигают использование ИИ в самых различных аспектах и отраслях, таких как развлечения, индустрия здравоохранения, искусство, творчество, и т. д.
Идея нейронных сетей и машинного обучения уже давно доступна и в MetaTrader 5. Например, в языке есть нативная поддержка матриц и векторов и архитектуры ONNX. Стало возможным создавать торговые модели с искусственным интеллектом любой сложности. Вам даже не нужно быть экспертом в линейной алгебре или других смежных науках, чтобы понимать все, что происходит в системе.
Несмотря на все это, сейчас труднее найти основы машинного обучения, чем когда-либо. Но без базовых знаний невозможно понять, как работает ИИ и как его можно использовать. Понимание того, что нужно делать и для чего, делает вас гибче и позволяет реализовать разные возможности. Есть очень много вещей, которые нам предстоит обсудить в области машинного обучения. Сегодня мы поговорим об алгоритмах оптимизации, узнаем, что это такое и как они соотносятся друг с другом, когда и какой алгоритм оптимизации следует выбрать для повышения производительности и точности нейронных сетей.
Тема, обсуждаемая в этой статье, поможет вам понять алгоритмы оптимизации в целом, то есть эти знания пригодятся вам даже при работе с моделями Scikit-Learn,Tensorflow или Pytorch из Python, так как эти оптимизаторы универсальны для всех нейронных сетей, независимо от того, какой язык программирования вы используете.
Что такое оптимизаторы нейронных сетей?
Согласно определению, оптимизаторы — это алгоритмы, которые точно настраивают параметры нейронной сети во время обучения. Их цель — минимизировать функцию потерь, что в конечном итоге приведет к повышению производительности.
Итак, оптимизаторы нейронных сетей:
- Являются ключевыми параметрами, которые влияют на нейронную сеть. Определяют, как изменить каждый параметр на каждой итерации обучения.
- Измеряют несоответствие между фактическими значениями и прогнозами нейронной сети. Пытаются постепенно уменьшить эту ошибку.
Для начала рекомендую ознакомиться со статьей "Разбираем нейронные сети", если вы ее еще не читали. В данной статье мы будем улучшать модель нейронной сети, которую построили с нуля предыдущей статье, добавив в нее оптимизаторы.
Прежде чем познакомимся с различными типами оптимизаторов, нам необходимо понять алгоритмы обратного распространения ошибки. Обычно выделяют три алгоритма:
- Стохастический градиентный спуск (Stochastic Gradient Descent, SGD)
- Пакетный градиентный спуск (Batch Gradient Descent BGD)
- Мини-пакетный градиентный спуск
01: Алгоритм стохастического градиентного спуска (SGD)
Стохастический градиентный спуск — это фундаментальный алгоритм оптимизации, используемый для обучения нейронных сетей. Он итеративно обновляет веса и смещения сети таким образом, чтобы минимизировать функцию потерь. Функция потерь измеряет несоответствие между предсказаниями сети и фактическими метками (целевыми значениями) в обучающих данных.
Основные процессы, задействованные в этих алгоритмах оптимизации, одинаковы. Они включают в себя следующие этапы:
- Итерация
- Обратное распространение ошибки
- Обновление весов и смещений
Эти алгоритмы различаются тем, как обрабатываются итерации и как часто обновляются веса и смещения. Алгоритм SGD обновляет параметры нейронной сети (веса и смещения) по одному обучающему примеру (точке данных) за раз.
void CRegressorNets::backpropagation(const matrix& x, const vector &y) { for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { for (ulong iter=0; iter<rows; iter++) //iterate through all data points { for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { // find partial derivatives of each layer WRT the loss function dW and dB //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.W_tensor.Add(W, layer); this.B_tensor.Add(B, layer); } } } }
Преимущества алгоритма:
- Вычислительная эффективность при работе с большими наборами данных.
- Иногда может сходиться быстрее, чем BGD и мини-пакетный градиентный спуск, особенно для невыпуклых функций потерь, поскольку использует одну обучающую выборку за раз.
- Хорошо избегает локальных минимумов: благодаря зашумленным обновлениям в SGD имеет возможность выходить за пределы локальных минимумов и сходиться к глобальным минимумам.
Минусы:
- Обновления могут быть зашумленными, что приводит к зигзагообразному поведению во время обучения.
- Может не всегда сходиться к глобальному минимуму.
- Медленно сходится, может потребоваться больше эпох, поскольку он обновляет параметры для каждого обучающего примера по одному.
- Чувствителен к скорости обучения. Выбор скорости обучения может очень сильно повлиять на результаты алгоритма: более высокая скорость обучения может привести к тому, что алгоритм выйдет за пределы глобальных минимумов, а более низкая скорость обучения замедляет процесс сходимости.
02: Пакетный алгоритм градиентного спуска (BGD):
В отличие от SGD, пакетный градиентный спуск (BGD) вычисляет градиенты, используя весь набор данных на каждой итерации.
Преимущества:
Теоретически сходится к минимуму, если функция потерь гладкая и выпуклая.
Минусы:
Для больших наборов данных может быть затратно в вычислительном отношении, так как требуется повторная обработка всего набора данных.
Я не буду реализовывать его в нашей нейронной сети, с которой мы работаем в данный момент, но его можно легко реализовать, как и описанный ниже мини-пакетный градиентный спуск. При желании вы сможете реализовать его самостоятельно.
03: Мини-пакетный градиентный спуск:
Этот алгоритм является компромиссом между SGD и BGD. Он обновляет параметры сети, используя небольшое подмножество (мини-пакет) обучающих данных на каждой итерации.
Преимущества:
- Обеспечивает хороший баланс между вычислительной эффективностью и стабильностью обновлений по сравнению с SGD и BGD.
- Может обрабатывать большие наборы данных более эффективно, чем BGD.
Минусы:
- Может потребоваться дополнительная настройка размера мини-пакета по сравнению с SGD.
- Вычислительно затратен по сравнению с SGD, потребляет много памяти для пакетного хранения и обработки.
- При большом количестве больших пакетов обучение может занять много времени.
Ниже приведен псевдокод того, как выглядит алгоритм мини-пакетного градиентного спуска:
void CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *sgd, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { //.... for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1)) { matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1); vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1); rows = batch_x.Rows(); for (ulong iter=0; iter<rows ; iter++) //replace to rows { pred_v[0] = predict(batch_x.Row(iter)); actual_v[0] = y[iter]; // Find derivatives WRT weights dW and bias dB //.... //--- Updating the weights using a given optimizer optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } } }
В основе этих двух алгоритмов по умолчанию есть Простое правило обновления градиентного спуска, которое обычно называют Оптимизатор SGD или Mini-BGD.
class OptimizerSGD { protected: double m_learning_rate; public: OptimizerSGD(double learning_rate=0.01); ~OptimizerSGD(void); virtual void update(matrix ¶meters, matrix &gradients); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerSGD::OptimizerSGD(double learning_rate=0.01): m_learning_rate(learning_rate) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerSGD::~OptimizerSGD(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OptimizerSGD::update(matrix ¶meters, matrix &gradients) { parameters -= this.m_learning_rate * gradients; //Simple gradient descent update rule } //+------------------------------------------------------------------+ //| Batch Gradient Descent (BGD): This optimizer computes the | //| gradients of the loss function on the entire training dataset | //| and updates the parameters accordingly. It can be slow and | //| memory-intensive for large datasets but tends to provide a | //| stable convergence. | //+------------------------------------------------------------------+ class OptimizerMinBGD: public OptimizerSGD { public: OptimizerMinBGD(double learning_rate=0.01); ~OptimizerMinBGD(void); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerMinBGD::OptimizerMinBGD(double learning_rate=0.010000): OptimizerSGD(learning_rate) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerMinBGD::~OptimizerMinBGD(void) { }
Теперь обучим модель с помощью этих двух оптимизаторов и посмотрим на результат, чтобы лучше понять их:
#include <MALE5\MatrixExtend.mqh> #include <MALE5\preprocessing.mqh> #include <MALE5\metrics.mqh> #include <MALE5\Neural Networks\Regressor Nets.mqh> CRegressorNets *nn; StandardizationScaler scaler; vector open_, high_, low_; vector hidden_layers = {5}; input uint nn_epochs = 100; input double nn_learning_rate = 0.0001; input uint nn_batch_size =32; input bool show_batch = false; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string headers; matrix dataset = MatrixExtend::ReadCsv("airfoil_noise_data.csv", headers); matrix x_train, x_test; vector y_train, y_test; MatrixExtend::TrainTestSplitMatrices(dataset, x_train, y_train, x_test, y_test, 0.7); nn = new CRegressorNets(hidden_layers, AF_RELU_, LOSS_MSE_); x_train = scaler.fit_transform(x_train); nn.fit(x_train, y_train, new OptimizerMinBGD(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); delete nn; }
Если параметру nn_batch_size установлено значение больше нуля, градиентный спуск Mini-Batch активирован независимо от того, какой оптимизатор применяется к функции обучения/обратного распространения ошибки.
backprop CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { //... //... //--- Optimizer use selected optimizer when batch_size ==0 otherwise use the batch gradient descent OptimizerSGD optimizer_weights = optimizer; OptimizerSGD optimizer_bias = optimizer; if (batch_size>0) { OptimizerMinBGD optimizer_weights; OptimizerMinBGD optimizer_bias; } //--- Cross validation CCrossValidation cross_validation; CTensors *cv_tensor; matrix validation_data = MatrixExtend::concatenate(x, y); matrix validation_x; vector validation_y; cv_tensor = cross_validation.KFoldCV(validation_data, 10); //k-fold cross validation | 10 folds selected //--- matrix DELTA = {}; double actual=0, pred=0; matrix temp_inputs ={}; matrix dB = {}; //Bias Derivatives matrix dW = {}; //Weight Derivatives for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { double epoch_start = GetTickCount(); uint num_batches = (uint)MathFloor(x.Rows()/(batch_size+DBL_EPSILON)); vector batch_loss(num_batches), batch_accuracy(num_batches); vector actual_v(1), pred_v(1), LossGradient = {}; if (batch_size==0) //Stochastic Gradient Descent { for (ulong iter=0; iter<rows; iter++) //iterate through all data points { pred = predict(x.Row(iter)); actual = y[iter]; pred_v[0] = pred; actual_v[0] = actual; //--- DELTA.Resize(mlp.outputs,1); for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { //..... backpropagation and finding derivatives code //-- Observation | DeLTA matrix is same size as the bias matrix W = this.Weights_tensor.Get(layer); B = this.Bias_tensor.Get(layer); //--- Derivatives wrt weights and bias dB = DELTA; dW = DELTA.MatMul(temp_inputs.Transpose()); //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } } else //Batch Gradient Descent { for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1)) { matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1); vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1); rows = batch_x.Rows(); for (ulong iter=0; iter<rows ; iter++) //iterate through all data points { pred_v[0] = predict(batch_x.Row(iter)); actual_v[0] = y[iter]; //--- DELTA.Resize(mlp.outputs,1); for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { //..... backpropagation and finding derivatives code } //-- Observation | DeLTA matrix is same size as the bias matrix W = this.Weights_tensor.Get(layer); B = this.Bias_tensor.Get(layer); //--- Derivatives wrt weights and bias dB = DELTA; dW = DELTA.MatMul(temp_inputs.Transpose()); //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } pred_v = predict(batch_x); batch_loss[batch] = pred_v.Loss(batch_y, ENUM_LOSS_FUNCTION(m_loss_function)); batch_loss[batch] = MathIsValidNumber(batch_loss[batch]) ? (batch_loss[batch]>1e6 ? 1e6 : batch_loss[batch]) : 1e6; //Check for nan and return some large value if it is nan batch_accuracy[batch] = Metrics::r_squared(batch_y, pred_v); if (show_batch_progress) printf("----> batch[%d/%d] batch-loss %.5f accuracy %.3f",batch+1,num_batches,batch_loss[batch], batch_accuracy[batch]); } } //--- End of an epoch vector validation_loss(cv_tensor.SIZE); vector validation_acc(cv_tensor.SIZE); for (ulong i=0; i<cv_tensor.SIZE; i++) { validation_data = cv_tensor.Get(i); MatrixExtend::XandYSplitMatrices(validation_data, validation_x, validation_y); vector val_preds = this.predict(validation_x);; validation_loss[i] = val_preds.Loss(validation_y, ENUM_LOSS_FUNCTION(m_loss_function)); validation_acc[i] = Metrics::r_squared(validation_y, val_preds); } pred_v = this.predict(x); if (batch_size==0) { backprop_struct.training_loss[epoch] = pred_v.Loss(y, ENUM_LOSS_FUNCTION(m_loss_function)); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan } else { backprop_struct.training_loss[epoch] = batch_loss.Mean(); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan } double epoch_stop = GetTickCount(); printf("--> Epoch [%d/%d] training -> loss %.8f accuracy %.3f validation -> loss %.5f accuracy %.3f | Elapsed %s ",epoch+1,epochs,backprop_struct.training_loss[epoch],Metrics::r_squared(y, pred_v),backprop_struct.validation_loss[epoch],validation_acc.Mean(),this.ConvertTime((epoch_stop-epoch_start)/1000.0)); } isBackProp = false; if (CheckPointer(optimizer)!=POINTER_INVALID) delete optimizer; return backprop_struct; }
Результаты:
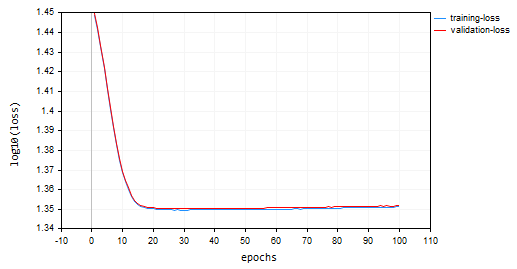
Стохастический градиентный спуск (SGD): скорость обучения = 0,0001.
Batch Gradient Descent(BGD): Learning rate = 0.0001, batch size = 16
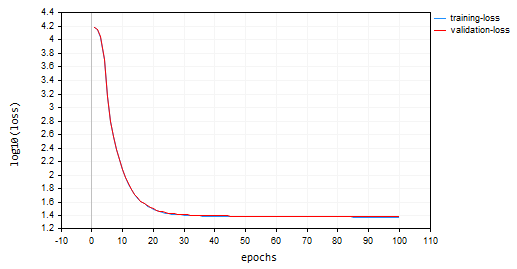
SGD сходился быстрее, был близок к локальным минимумам примерно к 10-й эпохе, в то время как BGD был примерно к 20-й эпохе, SGD сходился примерно с точностью 60 % как при обучении, так и при проверке, в то время как точность BGD составляла 15 % во время обучающей выборки и 13 % на проверочной выборке. Мы пока не можем сделать вывод, поскольку не уверены, что BGD имеет лучшую скорость обучения и размер пакета, подходящий для этого набора данных. Разные оптимизаторы лучше работают при разных скоростях обучения. Это может быть одной из причин неработоспособности SGD. И хотя он хорошо сходился без колебаний вокруг локальных минимумов, чего нельзя увидеть в SGD, так это плавны график как у BGD, что указывает на стабильный процесс обучения. Это связано с тем, что в BGD общая функция потери — это среднее значение потерь в отдельных пакетах.
backprop_struct.training_loss[epoch] = batch_loss.Mean(); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
Возможно, вы заметили на графиках, что к значениям потерь мы применили функцию log10. Эта нормализация гарантирует правильное отображение значений потерь, поскольку в ранние эпохи значения потерь иногда могут быть большими. Штрафуя большие значения, мы добиваемся того, чтобы они хорошо выглядели на графике. Реальные значения потерь можно увидеть во вкладке экспертов, а не на графике.
void CRegressorNets::fit(const matrix &x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { trained = true; //The fit method has been called vector epochs_vector(epochs); for (uint i=0; i<epochs; i++) epochs_vector[i] = i+1; backprop backprop_struct; backprop_struct = this.backpropagation(x, y, optimizer, epochs, batch_size, show_batch_progress); //Run backpropagation CPlots plt; backprop_struct.training_loss = log10(backprop_struct.training_loss); //Logarithmic scalling plt.Plot("Loss vs Epochs",epochs_vector,backprop_struct.training_loss,"epochs","log10(loss)","training-loss",CURVE_LINES); backprop_struct.validation_loss = log10(backprop_struct.validation_loss); plt.AddPlot(backprop_struct.validation_loss,"validation-loss",clrRed); while (MessageBox("Close or Cancel Loss Vs Epoch plot to proceed","Training progress",MB_OK)<0) Sleep(1); isBackProp = false; }
Оптимизатор SGD — это общий инструмент для минимизации функций потерь, а алгоритм SGD для обратного распространения ошибки — это особый метод SGD, предназначенный для расчета градиентов в нейронных сетях.
Оптимизатор SGD можно сравнить с плотником, а алгоритмы SGD или Min-BGD для обратного распространения ошибки — со специализированным инструментом в их наборе инструментов.
Типы оптимизаторов нейронных сетей
Помимо оптимизаторов SGD, которые мы только что обсуждали, существуют и другие различные оптимизаторы нейронных сетей, каждый из которых использует разные стратегии для достижения оптимальных значений параметров. Ниже приведены некоторые из наиболее часто используемых оптимизаторов нейронных сетей:
- Среднеквадратичное распространение (RMSProp)
- Адаптивный градиентный спуск (AdaGrad)
- Метод адаптивной оценки моментов (Adam)
- Adadelta
- Адаптивная оценка момента с ускорением Нестерова (Nadam)
01: Среднеквадратичное распространение (RMSProp)
Этот алгоритм оптимизации направлен на устранение ограничений стохастического градиентного спуска (SGD) путем адаптации скорости обучения для каждого параметра веса и смещения на основе их исторических градиентов.
Проблема с SGD:
SGD обновляет веса и смещения, используя текущий градиент и фиксированную скорость обучения. Однако в сложных функциях, коими и являются нейронные сети, величина градиентов может значительно различаться для разных параметров. Это может привести к медленному схождению, поскольку параметры с небольшими градиентами могут обновляться очень медленно, что также затрудняет общее обучение. Кроме того, SGD может вызвать большие колебания, поскольку параметры с большими градиентами могут испытывать чрезмерные колебания во время обновлений, что делает процесс обучения нестабильным.Теория:
Основная идея RMSprop:
- Используем для контроля экспоненциальное скользящее среднее (EMA) квадратов градиентов. Для каждого параметра RMSprop отслеживает экспоненциально убывающее среднее значение квадратов градиентов. Это среднее значение отражает необходимое обновление параметра.
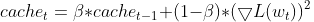
- Нормализуем градиент. Текущий градиент для каждого параметра делится на квадратный корень из EMA квадратов градиентов вместе с небольшим сглаживающим коэффициентом (обычно обозначаемым ε), который позволяет избежать деления на ноль.
- Обновляем параметры. Нормализованный градиент умножается на скорость обучения, чтобы определить обновление параметра.
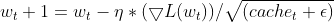
Где:
EMA квадратов градиентов на временном шаге t
Скорость затухания (гиперпараметр, обычно от 0,9 до 0,999) — контролирует влияние прошлых градиентов.
Градиент функции потерь по параметру w на временном шаге t
Значение параметра на временном шаге t
Обновленное значение параметра на временном шаге t+1.
η — скорость обучения (гиперпараметр)
ε — коэффициент сглаживания (обычно небольшое значение, например 1e-8).
class OptimizerRMSprop { protected: double m_learning_rate; double m_decay_rate; double m_epsilon; matrix<double> cache; //Dividing double/matrix causes compilation error | this is the fix to the issue matrix divide(const double numerator, const matrix &denominator) { matrix res = denominator; for (ulong i=0; i<denominator.Rows(); i++) res.Row(numerator / denominator.Row(i), i); return res; } public: OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8); ~OptimizerRMSprop(void); virtual void update(matrix& parameters, matrix& gradients); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerRMSprop::OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8): m_learning_rate(learning_rate), m_decay_rate(decay_rate), m_epsilon(epsilon) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerRMSprop::~OptimizerRMSprop(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OptimizerRMSprop::update(matrix ¶meters,matrix &gradients) { if (cache.Rows()!=parameters.Rows() || cache.Cols()!=parameters.Cols()) { cache.Init(parameters.Rows(), parameters.Cols()); cache.Fill(0.0); } //--- cache += m_decay_rate * cache + (1 - m_decay_rate) * MathPow(gradients, 2); parameters -= divide(m_learning_rate, cache + m_epsilon) * gradients; }
Мы выбрали 100 эпох и 0,0001 — это те же значения по умолчанию, которые использовались для предыдущих оптимизаторов. Нейронной сети не удалось сойтись в течение 100 эпох, она показала точность примерно -319 и -324 в обучающей и проверочной выборках соответственно. Похоже, что при таком темпе может потребоваться более 1000 эпох, если мы не превысим локальные минимумы для такого большого количества эпох.
HK 0 15:10:15.632 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 15164.85487215 accuracy -320.064 validation -> loss 15164.99272 accuracy -325.349 | Elapsed 0.031 Seconds HQ 0 15:10:15.663 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 15161.78717397 accuracy -319.999 validation -> loss 15161.92323 accuracy -325.283 | Elapsed 0.031 Seconds DO 0 15:10:15.694 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 15158.07142844 accuracy -319.921 validation -> loss 15158.20512 accuracy -325.203 | Elapsed 0.031 Seconds GE 0 15:10:15.727 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 15154.92004326 accuracy -319.854 validation -> loss 15155.05184 accuracy -325.135 | Elapsed 0.032 Seconds GS 0 15:10:15.760 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 15151.84229952 accuracy -319.789 validation -> loss 15151.97226 accuracy -325.069 | Elapsed 0.031 Seconds DH 0 15:10:15.796 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 15148.77653633 accuracy -319.724 validation -> loss 15148.90466 accuracy -325.003 | Elapsed 0.031 Seconds MF 0 15:10:15.831 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 15145.56414236 accuracy -319.656 validation -> loss 15145.69033 accuracy -324.934 | Elapsed 0.047 Seconds IL 0 15:10:15.869 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 15141.85430749 accuracy -319.577 validation -> loss 15141.97859 accuracy -324.854 | Elapsed 0.031 Seconds KJ 0 15:10:15.906 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 15138.40751503 accuracy -319.504 validation -> loss 15138.52969 accuracy -324.780 | Elapsed 0.032 Seconds PP 0 15:10:15.942 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 15135.31136641 accuracy -319.439 validation -> loss 15135.43169 accuracy -324.713 | Elapsed 0.046 Seconds NM 0 15:10:15.975 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 15131.73032246 accuracy -319.363 validation -> loss 15131.84854 accuracy -324.636 | Elapsed 0.032 Seconds
График потерь и эпох: 100 эпох, скорость обучения 0,0001.
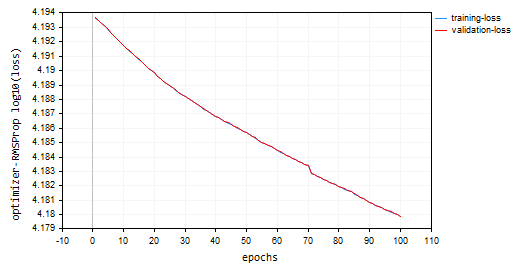
Где использовать RMSProp?
Этот алгоритм хорошо подходит для нестационарных целей, с редкими градиентами, он проще алгоритма Adam.
02: Adagrad (алгоритм адаптивного градиента)
Adagrad — оптимизатор нейронных сетей, использующий адаптивную скорость обучения, аналогичную RMSprop. Однако у Adagrad и RMSprop есть некоторые ключевые различия в подходах.
Расчеты, лежащие в основе метода:
- Накапливает прошлые градиенты. Adagrad отслеживает сумму квадратов градиентов для каждого параметра на протяжении всего процесса обучения. Это накопленное значение отражает, насколько параметр был обновлен в прошлом.
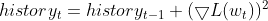
cache += MathPow(gradients, 2);
- Нормализует градиент. Текущий градиент для каждого параметра делится на квадратный корень из накопленной суммы квадратов градиентов вместе с небольшим сглаживающим коэффициентом (обычно обозначаемым ε), который позволяет избежать деления на ноль.
- Обновление параметра. Нормализованный градиент умножается на скорость обучения, чтобы определить обновление параметра.
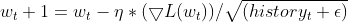
parameters -= divide(this.m_learning_rate, MathSqrt(cache + this.m_epsilon)) * gradients;
nn_learning_rate = 0.0001, epochs = 100
nn.fit(x_train, y_train, new OptimizerAdaGrad(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); График потерь и эпох:
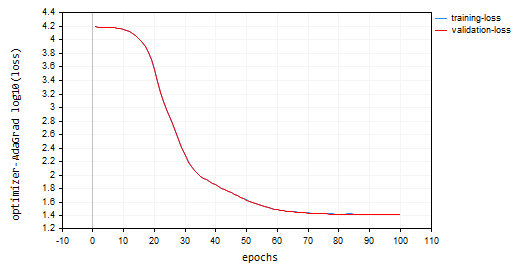
У Adagrad была более крутая кривая обучения, и он был очень стабильным во время обновлений, но для сходимости потребовалось более 100 эпох. В итоге он получил точность примерно 44% как для обучающей, так и для проверочной выборки.
RK 0 15:15:52.202 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 26.22261537 accuracy 0.445 validation -> loss 26.13118 accuracy 0.440 | Elapsed 0.031 Seconds ER 0 15:15:52.239 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 26.12443561 accuracy 0.447 validation -> loss 26.03635 accuracy 0.442 | Elapsed 0.047 Seconds NJ 0 15:15:52.277 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 26.11449352 accuracy 0.447 validation -> loss 26.02561 accuracy 0.442 | Elapsed 0.032 Seconds IQ 0 15:15:52.316 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 26.09263184 accuracy 0.448 validation -> loss 26.00461 accuracy 0.443 | Elapsed 0.046 Seconds NH 0 15:15:52.354 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 26.14277865 accuracy 0.447 validation -> loss 26.05529 accuracy 0.442 | Elapsed 0.032 Seconds HP 0 15:15:52.393 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 26.09559950 accuracy 0.448 validation -> loss 26.00845 accuracy 0.443 | Elapsed 0.047 Seconds PO 0 15:15:52.442 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 26.05409769 accuracy 0.448 validation -> loss 25.96754 accuracy 0.443 | Elapsed 0.046 Seconds PG 0 15:15:52.479 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 25.98822082 accuracy 0.450 validation -> loss 25.90384 accuracy 0.445 | Elapsed 0.032 Seconds PN 0 15:15:52.519 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 25.98781231 accuracy 0.450 validation -> loss 25.90438 accuracy 0.445 | Elapsed 0.047 Seconds EE 0 15:15:52.559 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 25.91146212 accuracy 0.451 validation -> loss 25.83083 accuracy 0.446 | Elapsed 0.031 Seconds CN 0 15:15:52.595 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 25.87412572 accuracy 0.452 validation -> loss 25.79453 accuracy 0.447 | Elapsed 0.047 Seconds
Преимущества метода Adagrad:
Он сходится быстрее для разреженных функций. В ситуациях, когда многие параметры обновляются нечасто из-за разреженных функций в данных, Adagrad может эффективно снизить скорость их обучения, обеспечивая более быструю сходимость этих параметров.
Ограничения метода Adagrad:
Со временем накопленная сумма квадратов градиентов в Adagrad продолжает расти, что приводит к постоянному снижению скорости обучения для всех параметров. В конечном итоге это может остановить прогресс в обучении.
Когда использовать Adagrad:
В разреженных наборах данных объектов: при работе с наборами данных, в которых многие объекты обновляются нечасто, Adagrad может эффективно ускорить сходимость этих параметров.
На ранних этапах обучения в некоторых случаях первоначальные корректировки скорости обучения с помощью Adagrad могут быть полезны перед переключением на другой оптимизатор на более позднем этапе обучения.
03: Адаптивная оценка момента (Adam)
Эффективный алгоритм оптимизации, широко используемый при обучении нейронных сетей. Сочетает в себе сильные стороны AdaGrad и RMSprop и обеспечивает эффективное и стабильное обучение.
Теория:
У алгоритма Adam есть две ключевые особенности:
- Экспоненциальное скользящее среднее (EMA) градиентов — как и RMSprop, Adam поддерживает EMA квадратов градиентов (кэш), чтобы фиксировать недавнюю историю обновлений, необходимых для каждого параметра.
- Экспоненциальное скользящее среднее моментов — метод Adam вводит еще одну EMA (момент), которая отслеживает скользящее среднее самих градиентов. Это позволяет частично облегчить проблему исчезновения градиентов, которая может возникнуть в некоторых сетевых архитектурах.
Нормализация и обновление:
- Обновление момента — текущий градиент используется для обновления EMA моментов (m_t).
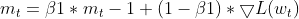
this.moment = this.m_beta1 * this.moment + (1 - this.m_beta1) * gradients;
- Обновление квадратного градиента — текущий квадратный градиент используется для обновления EMA квадратичных градиентов (cache_t).
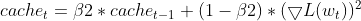
this.cache = this.m_beta2 * this.cache + (1 - this.m_beta2) * MathPow(gradients, 2);
- Коррекция смещения: обе EMA (moment_t и cache_t) корректируются на смещение с использованием коэффициентов экспоненциального затухания (β1 и β2), чтобы гарантировать, что они являются несмещенными оценками истинных моментов.
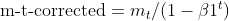
matrix moment_hat = this.moment / (1 - MathPow(this.m_beta1, this.time_step));
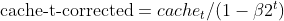
matrix cache_hat = this.cache / (1 - MathPow(this.m_beta2, this.time_step));
- Нормализация — аналогично RMSprop, градиент тока нормализуется с использованием скорректированных EMA и небольшого сглаживающего коэффициент (ε).
- Обновления параметров — нормализованный градиент умножается на скорость обучения (η), чтобы определить обновление параметра.
parameters -= (this.m_learning_rate * moment_hat) / (MathPow(cache_hat, 0.5) + this.m_epsilon);
Вот как выглядит конструктор оптимизатора Adam:
OptimizerAdam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double epsilon=1e-8);
Вызов со скоростью обучения:
nn.fit(x_train, y_train, new OptimizerAdam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); Итоговый график потерь и эпох:
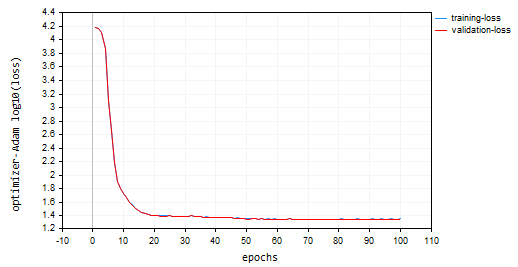
Алгоритм Adam показал лучшие результаты, чем предыдущие оптимизаторы, за исключением SGD. Он показал точность примерно 53% и 52% на обучающей и проверочной обучающей выборке соответственно.
MD 0 15:23:37.651 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 22.05051037 accuracy 0.533 validation -> loss 21.92528 accuracy 0.529 | Elapsed 0.047 Seconds DS 0 15:23:37.703 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 22.38393234 accuracy 0.526 validation -> loss 22.25178 accuracy 0.522 | Elapsed 0.046 Seconds OK 0 15:23:37.756 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 22.12091827 accuracy 0.532 validation -> loss 21.99456 accuracy 0.528 | Elapsed 0.063 Seconds OR 0 15:23:37.808 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 21.94438889 accuracy 0.535 validation -> loss 21.81944 accuracy 0.532 | Elapsed 0.047 Seconds NI 0 15:23:37.862 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 22.41965082 accuracy 0.525 validation -> loss 22.28371 accuracy 0.522 | Elapsed 0.062 Seconds LQ 0 15:23:37.915 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 22.27254037 accuracy 0.528 validation -> loss 22.13931 accuracy 0.525 | Elapsed 0.047 Seconds FH 0 15:23:37.969 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 21.93193893 accuracy 0.536 validation -> loss 21.80427 accuracy 0.532 | Elapsed 0.047 Seconds LG 0 15:23:38.024 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 22.41523220 accuracy 0.525 validation -> loss 22.27900 accuracy 0.522 | Elapsed 0.063 Seconds MO 0 15:23:38.077 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 22.23551304 accuracy 0.529 validation -> loss 22.10466 accuracy 0.526 | Elapsed 0.046 Seconds QF 0 15:23:38.129 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 21.96662717 accuracy 0.535 validation -> loss 21.84087 accuracy 0.531 | Elapsed 0.063 Seconds GM 0 15:23:38.191 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 22.29715377 accuracy 0.528 validation -> loss 22.16686 accuracy 0.524 | Elapsed 0.062 Seconds
Преимущества алгоритма Adam:
- Он сходится быстрее — Adam часто сходится быстрее, чем SGD, и может быть более эффективным, чем RMSprop в различных сценариях.
- Менее чувствителен к скорости обучения — по сравнению с SGD, Adam менее чувствителен к выбору скорости обучения, что делает его более надежным.
- Подходит для невыпуклых функций потерь — может эффективно обрабатывать невыпуклые функции потерь, распространенные в задачах глубокого обучения.
- Широкая применимость — сочетание функций алгоритма Adam делает его широко применимым оптимизатором для различных сетевых архитектур и наборов данных.
Минусы:
- Настройка гиперпараметров — несмотря на то, что Adam, как правило, менее чувствителен, для оптимальной производительности все же требуется настройка гиперпараметров, таких как скорость обучения и скорость затухания.
- Использование памяти — использование EMA может привести к несколько большему потреблению памяти по сравнению с SGD.
Где использовать метод Adam?
Метод Adam (Adaptive Moment Estimation) используется в нейронных сетях, когда вам нужно:
Более быстрое схождение. Нужно, чтобы ваша сеть была менее чувствительной к скорости обучения, или когда нужна адаптивная скорость обучения с большой скоростью.
04: Adadelta (Адаптивное обучение с дельтой)
Это еще один алгоритм оптимизации, используемый в нейронных сетях. Он имеет некоторое сходство с SGD и RMSProp, предлагая адаптивную скорость обучения с определенным моментом.
Adadelta стремится решить проблему фиксированной скорости обучения SGD, которая приводит к медленной сходимости и колебаниям. Алгоритм использует адаптивную скорость обучения, которая корректируется на основе прошлых квадратов градиентов, аналогично RMSProp.
Расчеты:
- Используя экспоненциальное скользящее среднее (EMA) квадратов дельт, Adadelta вычисляет EMA квадратов разностей между последовательными обновлениями параметров (дельтами) для каждого параметра. Это отражает недавнюю историю того, насколько сильно изменился параметр.
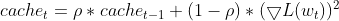
this.cache = m_decay_rate * this.cache + (1 - m_decay_rate) * MathPow(gradients, 2);
- Адаптивная скорость обучения — текущий квадрат градиента параметра делится на EMA квадратов дельт (со сглаживающим фактором). Получается адаптивная скорость обучения, при которой контролируется размер обновления для каждого параметра.
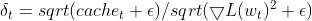
matrix delta = lr * sqrt(this.cache + m_epsilon) / sqrt(pow(gradients, 2) + m_epsilon);
-
Момент — Adadelta включает в себя импульс, который учитывает предыдущее обновление параметра, аналогично импульсу SGD. Это помогает накапливать градиенты и потенциально избегать локальных минимумов.
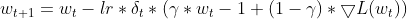
matrix momentum_term = this.m_gamma * parameters + (1 - this.m_gamma) * gradients; parameters -= delta * momentum_term;
где:
— EMA квадрата дельт на временном шаге t
— скорость затухания (гиперпараметр, обычно от 0,9 до 0,999)
— градиент функции потерь относительно параметра w на временном шаге t
— значение параметра на временном шаге t
— обновленное значение параметра на временном шаге t+1.
ε — коэффициент сглаживания (обычно небольшое значение, например 1e-8).
γ — коэффициент импульса (гиперпараметр, обычно от 0 до 1).
Преимущества оптимизатора Adadelta:
- Сходится быстрее — по сравнению с SGD с фиксированной скоростью обучения, Adadelta часто может сходиться быстрее, особенно для задач с нестационарными градиентами.
- Использует импульс для выхода из локальных минимумов — импульс помогает накапливать градиенты и потенциально избегать локальных минимумов в функции потерь.
- Менее чувствителен к скорости обучения — как и RMSprop, метод Adadelta менее чувствителен к выбранной конкретной скорости обучения, чем SGD.
Недостатки Adadelta:
- Требуется настройка гиперпараметров, таких как скорость затухания (ρ) и коэффициент импульса (γ), для оптимальной производительности.
OptimizerAdaDelta(double learning_rate=0.01, double decay_rate=0.95, double gamma=0.9, double epsilon=1e-8);
- Вычислительно затратно — поддержание EMA и учет импульса немного увеличивают вычислительные затраты по сравнению с SGD.
Когда использовать Adadelta
Adadelta может быть удобной альтернативой в определенных сценариях:
- Нестационарные градиенты. Если ваша задача демонстрирует нестационарные градиенты, адаптивная скорость обучения с импульсом Adadelta может оказаться полезной.
- В ситуациях, когда выход из локальных минимумов имеет решающее значение, использование импульса в Adadelta может помочь.
Я обучал модель с использованием adadelta на 100 эпохах со скоростью обучения 0,0001. Все параметры такие же, как и в других оптимизаторах:
nn.fit(x_train, y_train, new OptimizerAdaDelta(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); График потерь и эпох:
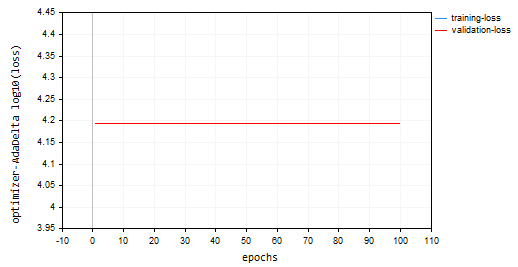
Оптимизатор Adadelta не смог обучиться, поскольку он показывал одинаковое значение потерь 15625 и точность примерно -335 на обучающих и проверочных выборках. Похоже на то, как это было с RMSProp.
NP 0 15:32:30.664 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds ON 0 15:32:30.724 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds IK 0 15:32:30.788 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds JQ 0 15:32:30.848 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds RO 0 15:32:30.914 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds PE 0 15:32:30.972 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds CS 0 15:32:31.029 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.047 Seconds DI 0 15:32:31.086 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds DG 0 15:32:31.143 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds FM 0 15:32:31.202 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.046 Seconds GI 0 15:32:31.258 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds
05: Адаптивная оценка момента с ускорением Нестерова Nadam
Этот алгоритм оптимизации сочетает в себе сильные стороны двух популярных оптимизаторов: Adam (Adaptive Moment Estimation) и Nesterov Momentum. Он направлен на достижение более быстрой сходимости и потенциально лучшей производительности по сравнению с методом Adam, особенно в ситуациях с зашумленными градиентами.
Подход метода Nadam:
Он наследует основные функции от оптимизатора Adam:
class OptimizerNadam: protected OptimizerAdam { protected: double m_gamma; public: OptimizerNadam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8); ~OptimizerNadam(void); virtual void update(matrix ¶meters, matrix &gradients); }; //+------------------------------------------------------------------+ //| Initializes the Adam optimizer with hyperparameters. | //| | //| learning_rate: Step size for parameter updates | //| beta1: Decay rate for the first moment estimate | //| (moving average of gradients). | //| beta2: Decay rate for the second moment estimate | //| (moving average of squared gradients). | //| epsilon: Small value for numerical stability. | //+------------------------------------------------------------------+ OptimizerNadam::OptimizerNadam(double learning_rate=0.010000, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8) :OptimizerAdam(learning_rate, beta1, beta2, epsilon), m_gamma(gamma) { }
В том числе:
-
EMA (экспоненциальных скользящих средних) — он отслеживает EMA квадратов градиентов (cache_t) и EMA моментов (m_t), как и Adam.
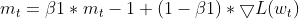
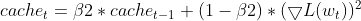
- Расчеты адаптивной скорости обучения — на основе этих EMA рассчитывается адаптивная скорость обучения, которая корректируется для каждого параметра.
- Включает в себя импульс Нестерова. Nadam использует концепцию импульса Нестерова. Это включает в себя:
- Градиент предсказания — перед обновлением параметра на основе текущего градиента Nadam оценивает градиент "заглядывания в будущее", используя текущий градиент и момент импульса.
- Обновление с помощью градиента предсказания — затем обновление параметров выполняется с использованием этого градиента "заглядывания в будущее" (peek), что потенциально приводит к более быстрой сходимости и улучшенной обработке зашумленных градиентов.
Расчет Nadam:
- Обновление EMA импульсов (так же, как у Adam)
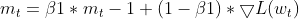
- Обновление EMA квадратов градиентов (как у Adam)
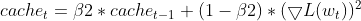
- Коррекция смещения на импульсы (как у Adam)
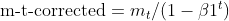
- Коррекция смещения для квадратов градиентов (как у Adam)
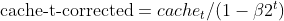
- Импульс Нестерова (с использованием предыдущей оценки градиента)
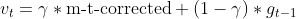
- Обновление предыдущей оценки градиента
- Обновление параметра с помощью импульса Нестерова
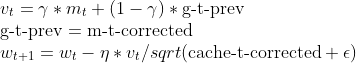
matrix nesterov_moment = m_gamma * moment_hat + (1 - m_gamma) * gradients; // Nesterov accelerated gradient parameters -= m_learning_rate * nesterov_moment / sqrt(cache_hat + m_epsilon); // Update parameters
Преимущества алгоритма Nadam:
- Это быстрее — по сравнению с методом Adam, Nadam потенциально может достичь более быстрой сходимости, особенно для проблем с зашумленными градиентами.
- Лучше справляется с шумными градиентами — импульс Нестерова в алгоритме Nadam может помочь сгладить шумные градиенты и привести к повышению производительности.
- Также обладает всеми преимуществами Adam, включая адаптивность и меньшую чувствительность к выбору скорости обучения.
Минусы:
- Для оптимальной производительности требуется настройка гиперпараметров: скорость обучения, скорость затухания и коэффициент импульса.
- Хотя Nadam кажется довольно перспективным, не во всех случаях работает лучше, чем Adam. Необходимы дальнейшие исследования и эксперименты.
Когда использовать метод Nadam?
Может стать отличной альтернативой алгоритму Adam в задачах, где есть шумные градиенты.
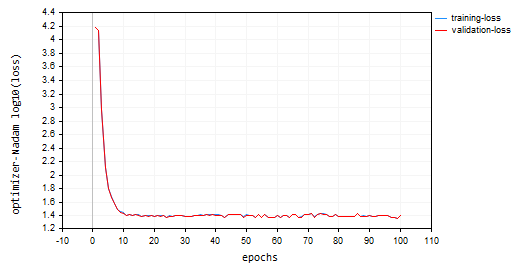
Я добавил вызов алгоритма Nadam с параметрами по умолчанию и той же скоростью обучения, которую мы использовали для всех ранее обсуждавшихся оптимизаторов. В итоге получил вторые по качеству результаты после Adam, точность примерно 47% как на обучающей, так и на проверочной выборке. Nadam совершил больше колебаний вокруг локальных минимумов, чем другие обсуждаемые в этой статье методы.
IL 0 15:37:56.549 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 25.23632476 accuracy 0.466 validation -> loss 25.06902 accuracy 0.462 | Elapsed 0.062 Seconds LK 0 15:37:56.619 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 24.60851222 accuracy 0.479 validation -> loss 24.44829 accuracy 0.475 | Elapsed 0.078 Seconds RS 0 15:37:56.690 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 24.68657614 accuracy 0.477 validation -> loss 24.53442 accuracy 0.473 | Elapsed 0.078 Seconds IJ 0 15:37:56.761 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 24.89495551 accuracy 0.473 validation -> loss 24.73423 accuracy 0.469 | Elapsed 0.063 Seconds GQ 0 15:37:56.832 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 25.25899364 accuracy 0.465 validation -> loss 25.09940 accuracy 0.461 | Elapsed 0.078 Seconds QI 0 15:37:56.901 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 25.17698272 accuracy 0.467 validation -> loss 25.01065 accuracy 0.463 | Elapsed 0.063 Seconds FP 0 15:37:56.976 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 25.36663261 accuracy 0.463 validation -> loss 25.20273 accuracy 0.459 | Elapsed 0.078 Seconds FO 0 15:37:57.056 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 23.34069092 accuracy 0.506 validation -> loss 23.19590 accuracy 0.502 | Elapsed 0.078 Seconds OG 0 15:37:57.128 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 23.48894694 accuracy 0.503 validation -> loss 23.33753 accuracy 0.499 | Elapsed 0.078 Seconds ON 0 15:37:57.203 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 23.03205165 accuracy 0.512 validation -> loss 22.88233 accuracy 0.509 | Elapsed 0.062 Seconds ME 0 15:37:57.275 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 24.98193438 accuracy 0.471 validation -> loss 24.82652 accuracy 0.467 | Elapsed 0.079 Seconds
Ниже приведен график потерь и эпох:
Заключительные мысли
Выбор лучшего оптимизатора зависит от вашей конкретной проблемы, набора данных, сетевой архитектуры и параметров. Эксперименты — ключ к поиску наиболее эффективного оптимизатора для вашей задачи обучения нейронной сети. Adam показал себя лучшим оптимизатором для многих нейронных сетей благодаря своей способности сходиться быстрее, он менее чувствителен к скорости обучения и адаптирует свою скорость обучения в зависимости от импульса. Это хороший вариант для первого выбора, особенно в случае сложной проблемы или когда вы не уверены, какой оптимизатор использовать изначально.
Удачи.
За развитием этой модели машинного обучения и многого другого из этой серии статей можно следить в моем репозиторий на GitHub.
Содержимое вложения:
| Файл | Описание/назначение |
|---|---|
| MatrixExtend.mqh | Дополнительные функции для работы с матрицами. |
| metrics.mqh | Функции и код для измерения производительности моделей машинного обучения. |
| preprocessing.mqh | Библиотека для предварительной обработки необработанных входных данных, чтобы сделать их пригодными для использования в моделях машинного обучения. |
| plots.mqh | Библиотека для построения векторов и матриц |
| optimizers.mqh | Include-файл, содержит все оптимизаторы нейронных сетей, обсуждаемые в этой статье. |
| cross_validation.mqh | Библиотека, содержащая методы перекрестной проверки. |
| Tensors.mqh | Библиотека, содержащая тензоры, объекты алгебраических 3D-матриц на простом языке MQL5. |
| Regressor Nets.mqh | Содержит нейронные сети для решения задачи регрессии. |
| Optimization Algorithms testScript.mq5 | Скрипт для запуска кода из всех включаемых файлов и набора данных. Это основной файл. |
| airfoil_noise_data.csv | Данные для задачи регрессии Airfoil |
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/14435
Возможности Мастера MQL5, которые вам нужно знать (Часть 14): Многоцелевое прогнозирование таймсерий с помощью STF
Разрабатываем мультивалютный советник (Часть 16): Влияние разных историй котировок на результаты тестирования
Разработка системы репликации (Часть 43): Проект Chart Trade (II)
Возможности Мастера MQL5, которые вам нужно знать (Часть 13): DBSCAN для класса сигналов советника
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Скрипт из статьи выдаёт ошибку:
2024.11.21 15:09:16.213 Optimization Algorithms testScript (EURUSD,M1) Zero divide, check divider for zero to avoid this error in 'D:\Market\MT5\MQL5\Scripts\Optimization Algorithms testScript.ex5'
Скрипт из статьи выдаёт ошибку:
2024.11.21 15:09:16.213 Optimization Algorithms testScript (EURUSD,M1) Zero divide, check divider for zero to avoid this error in 'D:\Market\MT5\MQL5\Scripts\Optimization Algorithms testScript.ex5'
Проблема оказалась в том, что скрипт не нашел файл с данными для обучения. Но, в любом случае, программой должен обрабатываться такой случай, если файл с данными не найден.
Но теперь такая проблема:
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 50 undeleted dynamic objects found:
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 10 objects of class 'CTensors'
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 40 objects of class 'CMatrix'
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 14816 bytes of leaked memory found
Проблема оказалась в том, что скрипт не нашел файл с данными для обучения. Но, в любом случае, программой должен обрабатываться такой случай, если файл с данными не найден.
Но теперь такая проблема:
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 50 undeleted dynamic objects found:
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 10 objects of class 'CTensors'
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 40 objects of class 'CMatrix'
2024.11.21 17:27:37.038 Optimization Algorithms testScript (EURUSD,M1) 14816 bytes of leaked memory found
Это связано с тем, что для одного экземпляра класса должна быть вызвана только одна функция «подгонки». Я вызвал несколько функций подгонки, что приводит к созданию нескольких тензоров в памяти. Это было в образовательных целях.
Это должно быть так;