MetaTrader 5 / Трейдинг
English Deutsch 日本語
preview
Машинное обучение и Data Science (Часть 16): Свежий взгляд на деревья решений

Машинное обучение и Data Science (Часть 16): Свежий взгляд на деревья решений

MetaTrader 5 — Трейдинг | 9 апреля 2024, 14:39
433 0
Omega J Msigwa
Omega J Msigwa

Краткий обзор

В одной из предыдущих статей данной серии я рассказывал о деревьях решений. Мы познакомились с тем, что такое деревья решений, и создали алгоритм для классификации данных о погоде. Однако код и объяснения, представленные в той статье, по-видимому, оказались недостаточно ясными, поскольку мне продолжают поступать сообщения с просьбой предоставить более эффективный подход к построению деревьев решений. Именно поэтому я посчитал, что может быть целесообразным написать вторую статьи и предоставить более качественный код. Кроме того, хорошее понимание деревьев решений очень важно для перехода к следующему этапу — алгоритмам случайного леса, о которых мы поговорим в следующих статьях.

Что такое дерево решений?

Дерево решений — это древовидная структура, подобная блок-схеме, где каждый внутренний узел представляет собой проверку атрибута (или признака), каждая ветвь — результат проверки, а каждый листовой узел — метку класса или непрерывное значение. Самый верхний узел в дереве решений известен как "корень", а листья — это результаты или прогнозы.

Что такое узел?

В дереве решений узел — это фундаментальный компонент, представляющий точку принятия решения на основе определенного признака или атрибута. В дереве решений есть два основных типа узлов: внутренние и листовые.

Внутренний узел

  • Внутренний узел — это точка принятия решения в дереве, где выполняется проверка определенного признака. Проверка основана на определенном условии, например, превышает ли значение признака пороговое значение или принадлежит ли он определенной категории.
  • Внутренние узлы имеют ветви (ребра), ведущие к дочерним узлам. Результат проверки определяет, по какой ветке идти дальше.
  • Внутренние узлы, которые представляют собой два левых и правых дочерних узла, являются узлами внутри центрального узла дерева.

Листовой узел (или терминальный узел)
  • Листовой узел — конечная точка в дереве, где принимается окончательное решение или прогноз. Он обозначает метку класса в задаче классификации или прогнозируемое значение в задаче регрессии.
  • Листовые узлы не имеют исходящих из них ветвей, они являются конечными точками процесса принятия решений.
  • В коде мы будем представлять их переменной типа double.
    class Node
{
  public:
    // for decision node
       
    uint feature_index;
    double threshold;
    double info_gain;
     
    // for leaf node
     
    double leaf_value;   
      
    Node *left_child;  //left child Node
    Node *right_child; //right child Node

    Node() : left_child(NULL), right_child(NULL) {} // default constructor

    Node(uint feature_index_, double threshold_=NULL, Node *left_=NULL, Node *right_=NULL, double info_gain_=NULL, double value_=NULL)
        : left_child(left_), right_child(right_)
    {
        this.feature_index = feature_index_;
        this.threshold = threshold_;
        this.info_gain = info_gain_;
        this.value = value_;
    }
    
   void Print()
    {
      printf("feature_index: %d \nthreshold: %f \ninfo_gain: %f \nleaf_value: %f",feature_index,threshold, info_gain, value);
    }    
};

    В отличие от некоторых алгоритмов машинного обучения, которые мы с нуля писали в рамках этой серии, дерево решений может быть сложным для представления в коде и временами запутанным, поскольку для реализации деревьев требуется использовать рекурсивные классы и функции. По моему опыту, такое может быть очень сложно представить на каком-либо языке отличном от Python.

    Компоненты узла:

    Узел в дереве решений обычно содержит следующую информацию:

    01. Условия проверки

    Внутренние узлы имеют условия проверки, основанные на определенном признаке и пороговом значении или категории. Это условие определяет, как данные разбиваются на дочерние узлы.

    Вы не видите условие проверки в этом классе Node. Мы реализуем его внутри функции build_tree, которая интегрируется с классом узла, поскольку возвращает экземпляр класса узла. 
    Node *build_tree(matrix &data, uint curr_depth=0);

    02. Признак и пороговое значение

    Указывает, какой признак проверяется на узле, а также пороговое значение или категорию, используемую для разделения.

    uint feature_index;
double threshold;

    03. Метка класса или значение

    Листовой узел хранит метку прогнозируемого класса (для классификации) или значение (для регрессии). 

    double leaf_value;  

    04. Дочерние узлы

    Внутренние узлы имеют дочерние, соответствующие различным результатам условия проверки. Каждый дочерний узел представляет собой подмножество данных, удовлетворяющее условию. 

    Node *left_child;  //left child Node
Node *right_child; //right child Node

    Пример:

    Рассмотрим простое дерево решений для классификации того, является ли фрукт яблоком или апельсином, на основе его цвета.

    [Узел]

    Признак: цвет

    Условие проверки: цвет красный?

    Если True, переходим к левому дочернему элементу, а если false — к правому

    [Листовой узел — яблоко]

    -Метка класса: яблоко

    [Листовой узел — апельсин]

    -Метка класса: апельсин

    Типы деревьев решений:

    Деревья классификации и регрессии CART (Classification and Regression Trees) — используются как для задач классификации, так и для регрессии. Разделяет данные на основе критерия Джини в случае классификации и среднеквадратической ошибки в случае регрессии.

    ID3 (итеративный дихотомизатор 3) — в основном используется для задач классификации. Использует концепцию энтропии и прироста информации для принятия решений.

    C4.5 — улученная версия ID3, используемая для классификации. Использует коэффициент прироста для устранения смещения в сторону атрибутов с большим количеством уровней.

    Поскольку мы будем использовать дерево решений для целей классификации, будем строить алгоритм ID3, который работает на основе прироста информации, расчета критериев и категориальных характеристик:


    ID3 (Итеративный дихотомизатор 3)

    ID3 использует информационный критерий прироста информации для выбора наилучшего разделения данных на каждом внутреннем узле дерева. Критерий прироста информации измеряет снижение энтропии или неопределенности после разделения набора данных. 
    double CDecisionTree::information_gain(vector &parent, vector &left_child, vector &right_child)
 {  
    double weight_left = left_child.Size() / (double)parent.Size(),
           weight_right = right_child.Size() / (double)parent.Size();
    
    double gain =0;    
    switch(m_mode)
      {
       case  MODE_GINI:
         gain = gini_index(parent) - ( (weight_left*gini_index(left_child)) + (weight_right*gini_index(right_child)) );
         break;
       case MODE_ENTROPY:
         gain = entropy(parent) - ( (weight_left*entropy(left_child)) + (weight_right*entropy(right_child)) );
         break;
      }
    
   return gain;
 }

    Энтропия — мера неопределенности или беспорядка в наборе данных. Алгоритм ID3 стремится уменьшить энтропию, выбирая разделение признаков, в результате которого получаются подмножества с более однородными метками классов.

    double CDecisionTree::entropy(vector &y)
 {    
   vector class_labels = matrix_utils.Unique_count(y);
     
   vector p_cls = class_labels / double(y.Size());
  
   vector entropy = (-1 * p_cls) * log2(p_cls);
  
  return entropy.Sum();
 }

    Чтобы получить большую гибкость, можно выбирать между энтропией и критерием Джини, который также часто используется в деревьях решений и выполняет ту же работу, что и функция энтропии. Они оба оценивают примеси или беспорядок в наборе данных.

    double CDecisionTree::gini_index(vector &y)
 {
   vector unique = matrix_utils.Unique_count(y);
   
   vector probabilities = unique / (double)y.Size();
   
   return 1.0 - MathPow(probabilities, 2).Sum();
 }

    Формулы расчета этих значений:


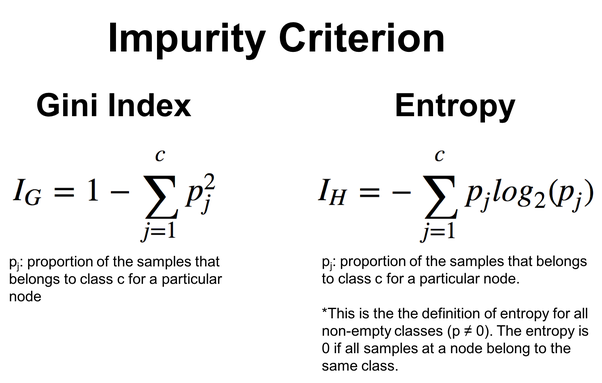
    Алгоритм ID3 особенно подходит для категориальных признаков, а выбор признаков и пороговых значений основан на уменьшении энтропии для разделения на категории. Мы увидим этот принцип в действии на пример алгоритма дерева решений ниже.


    Алгоритм дерева решений

    01. Критерии разделения

    Стандартными критериями для разделения данных при классификации являются коэффициент Джини и энтропия, а для задач регрессии — это среднеквадратическая ошибка. Давайте остановимся на функциях разделения алгоритма дерева решений, которые начинаются со структуры для сохранения информации для данных, которые нужно разделить. 

    //A struct containing splitted data information
struct split_info
  {
   uint feature_index;
   double threshold;
   matrix dataset_left,
          dataset_right;
   double info_gain;
  };

    Используя пороговое значение, разделим данные и поместим объекты со значениями меньше этого порога в матрицу dataset_left, а остальные — в dataset_right. После этого вернем экземпляр структуры Split_info. 

    split_info CDecisionTree::split_data(const matrix &data, uint feature_index, double threshold=0.5)
 {
   int left_size=0, right_size =0;
   vector row = {};
   
   split_info split;
   
   ulong cols = data.Cols();
   
   split.dataset_left.Resize(0, cols);
   split.dataset_right.Resize(0, cols);
      
    for (ulong i=0; i<data.Rows(); i++)
     {       
       row = data.Row(i);
       
       if (row[feature_index] <= threshold)
        {
          left_size++;
          split.dataset_left.Resize(left_size, cols);
          split.dataset_left.Row(row, left_size-1); 
        }
       else
        {
         right_size++;
         split.dataset_right.Resize(right_size, cols);
         split.dataset_right.Row(row, right_size-1);         
        }
     }
   return split;
 }

    Из множества разбиений алгоритму необходимо определить лучшее, то есть то, которое дает максимальный информационный прирост.

    split_info CDecisionTree::get_best_split(matrix &data, uint num_features)
  {
  
   double max_info_gain = -DBL_MAX;
   vector feature_values = {};
   vector left_v={}, right_v={}, y_v={};
   
//---
   
   split_info best_split;
   split_info split;
   
   for (uint i=0; i<num_features; i++)
     {
       feature_values = data.Col(i);
       vector possible_thresholds = matrix_utils.Unique(feature_values); //Find unique values in the feature, representing possible thresholds for splitting.
                  
         for (uint j=0; j<possible_thresholds.Size(); j++)
            {              
              split = this.split_data(data, i, possible_thresholds[j]);
              
              if (split.dataset_left.Rows()>0 && split.dataset_right.Rows() > 0)
                {
                  y_v = data.Col(data.Cols()-1);
                  right_v = split.dataset_right.Col(split.dataset_right.Cols()-1);
                  left_v = split.dataset_left.Col(split.dataset_left.Cols()-1);
                  
                  double curr_info_gain = this.information_gain(y_v, left_v, right_v);
                                    
                  if (curr_info_gain > max_info_gain) // Check if the current information gain is greater than the maximum observed so far.
                    {             
                      #ifdef DEBUG_MODE
                        printf("split left: [%dx%d] split right: [%dx%d] curr_info_gain: %f max_info_gain: %f",split.dataset_left.Rows(),split.dataset_left.Cols(),split.dataset_right.Rows(),split.dataset_right.Cols(),curr_info_gain,max_info_gain);
                      #endif 
                      
                      best_split.feature_index = i;
                      best_split.threshold = possible_thresholds[j];
                      best_split.dataset_left = split.dataset_left;
                      best_split.dataset_right = split.dataset_right;
                      best_split.info_gain = curr_info_gain;
                      
                      max_info_gain = curr_info_gain;
                    }
                }
            }    
     }
     
    return best_split;
  }

    Функция ищет общие характеристики и возможные пороговые значения, чтобы найти лучшее разделение, которое максимизирует прирост информации. Результатом является структура split_info, содержащая информацию об объекте, пороговом значении и подмножествах, связанных с лучшим разделением.



    02. Построение древа

    Деревья решений строятся путем рекурсивного разделения набора данных на основе признаков до тех пор, пока не будет выполнено условие остановки (например, достижение определенной глубины или минимального количества выборок). 

    Node *CDecisionTree::build_tree(matrix &data, uint curr_depth=0)
 {
    matrix X;
    vector Y;
      
    matrix_utils.XandYSplitMatrices(data,X,Y); //Split the input matrix into feature matrix X and target vector Y.
    
    ulong samples = X.Rows(), features = X.Cols(); //Get the number of samples and features in the dataset.
        
    Node *node= NULL; // Initialize node pointer
            
    if (samples >= m_min_samples_split && curr_depth<=m_max_depth)
      {
         split_info best_split = this.get_best_split(data, (uint)features);
         
         #ifdef DEBUG_MODE
          Print("best_split left: [",best_split.dataset_left.Rows(),"x",best_split.dataset_left.Cols(),"]\nbest_split right: [",best_split.dataset_right.Rows(),"x",best_split.dataset_right.Cols(),"]\nfeature_index: ",best_split.feature_index,"\nInfo gain: ",best_split.info_gain,"\nThreshold: ",best_split.threshold);
         #endif 
                  
         if (best_split.info_gain > 0)
           {
             Node *left_child = this.build_tree(best_split.dataset_left, curr_depth+1);
             Node *right_child = this.build_tree(best_split.dataset_right, curr_depth+1);
                          
             node = new Node(best_split.feature_index,best_split.threshold,left_child,right_child,best_split.info_gain);
             return node;
           }
      }      
     
     node = new Node();
     node.leaf_value = this.calculate_leaf_value(Y);
          
     return node;
 }

    if (best_split.info_gain > 0):

    Строка кода выше проверяет, получена ли информация.

    Внутри этого блока происходит следующее:

    Node *left_child = this.build_tree(best_split.dataset_left, curr_depth+1);

    Рекурсивно создаем левый дочерний узел.

    Node *right_child = this.build_tree(best_split.dataset_right, curr_depth+1);

    Рекурсивно создаем правильный дочерний узел.

    node = new Node(best_split.feature_index, best_split.threshold, left_child, right_child, best_split.info_gain);

    Создаем узел принятия решений с информацией из наилучшего разделения.

    node = new Node();      

    Если дальнейшее разделение не требуется, создаем новый листовой узел.

    node.value = this.calculate_leaf_value(Y);

    Установим значение листового узла, используя функцию calculate_leaf_value.

    return node;

    Вернем узел, представляющий текущее разделение или лист.

    Для более удобной работы с функциями функцию build_tree можно оставить внутри функции fit, которая обычно используется в модулях машинного обучения в Python.

    void CDecisionTree::fit(matrix &x, vector &y)
 {
   matrix data = matrix_utils.concatenate(x, y, 1);
   
   this.root = this.build_tree(data);
 }

    Делаем прогнозы при обучении и тестирование модели

    vector CDecisionTree::predict(matrix &x)
 {
    vector ret(x.Rows());
    
    for (ulong i=0; i<x.Rows(); i++)
       ret[i] = this.predict(x.Row(i));
       
   return ret;
 }

    Делаем прогнозы в реальном времени

    double CDecisionTree::predict(vector &x)
 {     
   return this.make_predictions(x, this.root);
 }

    Вся связанная с этим грязная работа делается в функции make_predictions:

    double CDecisionTree::make_predictions(vector &x, const Node &tree)
 {
    if (tree.leaf_value != NULL) // This is a leaf leaf_value
      return tree.leaf_value;
      
    double feature_value = x[tree.feature_index];
    double pred = 0;
    
    #ifdef DEBUG_MODE
      printf("Tree.threshold %f tree.feature_index %d leaf_value %f",tree.threshold,tree.feature_index,tree.leaf_value);
    #endif 
    
    if (feature_value <= tree.threshold)
      {
       pred = this.make_predictions(x, tree.left_child);  
      }
    else
     {
       pred = this.make_predictions(x, tree.right_child);
     }
     
   return pred;
 }

    Подробнее об этой функции:

    Проверяем, меньше ли значение признака порогового значения текущего узла или равно ему. 
    if (feature_value <= tree.threshold):

    Внутри этого блока происходит следующее:

    Рекурсивно вызываем функцию make_predictions для левого дочернего узла. 

    pred = this.make_predictions(x, *tree.left_child);

    Иначе, если (Else, If) значение признака превышает пороговое значение:

    Рекурсивно вызываем функцию make_predictions для правого дочернего узла. 

    pred = this.make_predictions(x, *tree.right_child);
    return pred;

     Возвращаем прогноз.

    Вычисляем значения листа

    Функция ниже вычисляет значение листа:

    double CDecisionTree::calculate_leaf_value(vector &Y)
 {   
   vector uniques = matrix_utils.Unique_count(Y);
   vector classes = matrix_utils.Unique(Y);
   
   return classes[uniques.ArgMax()];
 }

    Функция возвращает элемент из Y с наибольшим количеством, т.е. находит наиболее распространенный элемент в списке.


    Все это сводится к классу CDecisionTree

    enum mode {MODE_ENTROPY, MODE_GINI};

class CDecisionTree
  {
CMatrixutils   matrix_utils;

protected:
      
   Node *build_tree(matrix &data, uint curr_depth=0);
   double  calculate_leaf_value(vector &Y);
   
//---
   
   uint m_max_depth;
   uint m_min_samples_split;
   
   mode m_mode;
   
   double  gini_index(vector &y);
   double  entropy(vector &y);
   double  information_gain(vector &parent, vector &left_child, vector &right_child);
   
   
   split_info  get_best_split(matrix &data, uint num_features);
   split_info  split_data(const matrix &data, uint feature_index, double threshold=0.5);
   
   double make_predictions(vector &x, const Node &tree);
   void delete_tree(Node* node);
   
public:
                     Node *root;
                     
                     CDecisionTree(uint min_samples_split=2, uint max_depth=2, mode mode_=MODE_GINI);
                    ~CDecisionTree(void);
                    
                     void fit(matrix &x, vector &y);
                     void print_tree(Node *tree, string indent=" ",string padl="");
                     double predict(vector &x);
                     vector predict(matrix &x);
  };

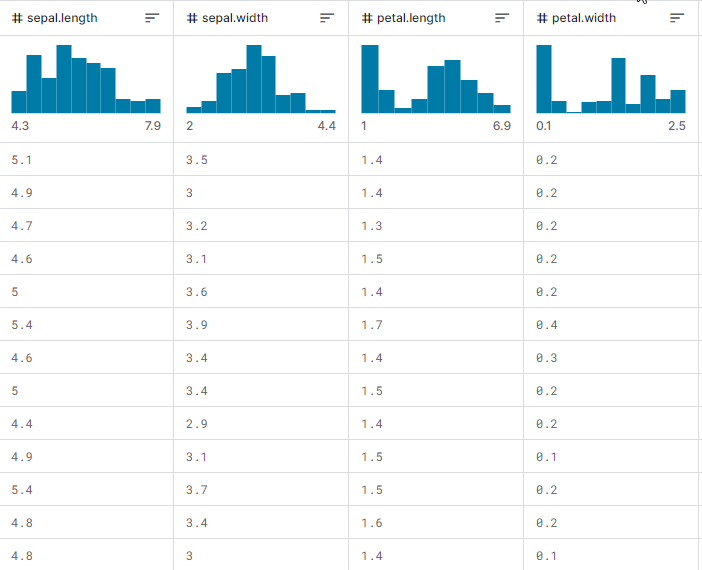
    Теперь давайте посмотрим, как все работает в действии, как построить дерево и как использовать его для прогнозирования при обучении и тестировании, а также в торговле в реальном времени. Давайте поработаем с выборкой данных iris-CSV и проверим работу класса.

    Обучать модель дерева решений будем при каждой инициализации советника, начиная с загрузки обучающих данных из файла CSV:

    int OnInit()
  {
  matrix dataset = matrix_utils.ReadCsv("iris.csv"); //loading iris-data
  
  decision_tree = new CDecisionTree(3,3, MODE_GINI); //Initializing the decision tree
  
  matrix x; vector y;
  matrix_utils.XandYSplitMatrices(dataset,x,y); //split the data into x and y matrix and vector respectively
  
  
  decision_tree.fit(x, y);  //Building the tree
  decision_tree.print_tree(decision_tree.root); //Printing the tree
  
  vector preds = decision_tree.predict(x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(y, preds)); //Measuring the accuracy
  
   return(INIT_SUCCEEDED);
  }

    Так выглядит при выводе матрица набора данных. Последний столбец прошел через энкодер. Один (1) означает Setosa, два (2) означает Versicolor и три (3) означает Virginica.

    Print("iris-csv\n",dataset);
    MS      0       08:54:40.958    DecisionTree Test (EURUSD,H1)   iris-csv
PH      0       08:54:40.958    DecisionTree Test (EURUSD,H1)   [[5.1,3.5,1.4,0.2,1]
CO      0       08:54:40.958    DecisionTree Test (EURUSD,H1)    [4.9,3,1.4,0.2,1]
...
...

NS      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [5.6,2.7,4.2,1.3,2]
JK      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [5.7,3,4.2,1.2,2]
...
...

NQ      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [6.2,3.4,5.4,2.3,3]
PD      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [5.9,3,5.1,1.8,3]]

    Вывод дерева

    Если внимательно посмотреть на код, можно заметить функцию print_tree, которая принимает корень дерева в качестве одного из аргументов. Эта функция пытается вывести в журнал общий вид дерева. Давайте подробнее посмотрим на ее работу.

    void CDecisionTree::print_tree(Node *tree, string indent=" ",string padl="")
  {
     if (tree.leaf_value != NULL)
        Print((padl+indent+": "),tree.leaf_value); 
     else //if we havent' reached the leaf node keep printing child trees
       {
         padl += " ";
         
         Print((padl+indent)+": X_",tree.feature_index, "<=", tree.threshold, "?", tree.info_gain);
         
         print_tree(tree.left_child, "left","--->"+padl);
         
         print_tree(tree.right_child, "right","--->"+padl);
       }
  }  

    Подробнее об этой функции:

    Структура узла:

    Функция предполагает, что класс Node представляет дерево решений. Каждый узел может быть либо узлом принятия решений, либо конечным узлом. Узлы решений имеют индекс признака feature_index, порог threshold, прирост информации info_gain и значение листа leaf_value.

    Вывод узла решения:

    Если текущий узел не является конечным узлом (т. е. tree.leaf_value имеет значение NULL), функция выводит информацию об узле принятия решения. Выводится условие для разделения, например, "X_2 <= 1.9 ? 0.33" и уровень отступа.

    Вывод листового узла:

    Если текущий узел является листовым (т.е. tree.leaf_value не равен NULL), она выводит конечное значение вместе с уровнем отступа. Например, "left: 0.33".

    Рекурсия:

    Затем функция рекурсивно вызывает себя для левого и правого дочернего элемента текущего узла Node. Аргумент padl добавляет отступ к сообщению, делая древовидную структуру более читабельной.

    Вывод print_tree для дерева решений, построенного внутри функции OnInit:

    CR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)     : X_2<=1.9?0.3333333333333334
HO      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   ---> left: 1.0
RH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->  right: X_3<=1.7?0.38969404186795487
HP      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->   left: X_2<=4.9?0.08239026063100136
KO      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_3<=1.6?0.04079861111111116
DH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 2.0
HM      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 3.0
HS      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_3<=1.5?0.2222222222222222
IH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 3.0
QM      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 2.0
KP      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->   right: X_2<=4.8?0.013547574039067499
PH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_0<=5.9?0.4444444444444444
PE      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 2.0
DP      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 3.0
EE      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->   right: 3.0

    Впечатляет.

    Ниже приведена точность нашей обученной модели:

      vector preds = decision_tree.predict(x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(y, preds)); //Measuring the accuracy

    Результат

    PM      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Confusion Matrix
CE      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   [[50,0,0]
HR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)    [0,50,0]
ND      0       09:26:39.990    DecisionTree Test (EURUSD,H1)    [0,1,49]]
GS      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   
KF      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Classification Report
IR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   
MD      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
EQ      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   1.0    50.00     50.00     100.00       50.00     50.0
HR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   2.0    51.00     50.00     100.00       50.50     50.0
PO      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   3.0    49.00     50.00     100.00       49.49     50.0
EH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   
PR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.99
HQ      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Average   50.00    50.00    100.00      50.00    150.0
DJ      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   W Avg     50.00    50.00    100.00      50.00    150.0
LG      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Train Acc = 0.993

    Мы достигли точности 99,3%, что указывает на успешную реализацию нашего дерева решений. Эта точность соответствует той, что мы ожидали бы от модели Scikit-Learn при решении простой проблемы с набором данных.

    Давайте продолжим обучение и протестируем модель на данных за пределами выборки.

      matrix train_x, test_x;
  vector train_y, test_y;
  
  matrix_utils.TrainTestSplitMatrices(dataset, train_x, train_y, test_x, test_y, 0.8, 42); //split the data into training and testing samples

  
  decision_tree.fit(train_x, train_y);  //Building the tree
  decision_tree.print_tree(decision_tree.root); //Printing the tree
  
  vector preds = decision_tree.predict(train_x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(train_y, preds)); //Measuring the accuracy
  
//---

  preds = decision_tree.predict(test_x); //making the predictions on a test data
  
  Print("Test Acc = ",metrics.confusion_matrix(test_y, preds)); //Measuring the accuracy

    Результат

    QD      0       14:56:03.860    DecisionTree Test (EURUSD,H1)     : X_2<=1.7?0.34125
LL      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   ---> left: 1.0
QK      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->  right: X_3<=1.6?0.42857142857142855
GS      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->   left: X_2<=4.9?0.09693877551020412
IL      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->   left: 2.0
MD      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_3<=1.5?0.375
IS      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 3.0
QR      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 2.0
RH      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->  right: 3.0
HP      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Confusion Matrix
FG      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   [[42,0,0]
EO      0       14:56:03.860    DecisionTree Test (EURUSD,H1)    [0,39,0]
HK      0       14:56:03.860    DecisionTree Test (EURUSD,H1)    [0,0,39]]
OL      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   
KE      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Classification Report
QO      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   
MQ      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
OQ      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   1.0    42.00     42.00     78.00       42.00     42.0
ML      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   3.0    39.00     39.00     81.00       39.00     39.0
HK      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   2.0    39.00     39.00     81.00       39.00     39.0
OE      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   
EO      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Accuracy                                   1.00
CG      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Average   40.00    40.00    80.00      40.00    120.0
LF      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   W Avg     40.05    40.05    79.95      40.05    120.0
PR      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Train Acc = 1.0
CD      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Confusion Matrix
FO      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   [[9,2,0]
RK      0       14:56:03.861    DecisionTree Test (EURUSD,H1)    [1,10,0]
CL      0       14:56:03.861    DecisionTree Test (EURUSD,H1)    [2,0,6]]
HK      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   
DQ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Classification Report
JJ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   
FM      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
QM      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   2.0    12.00     11.00     19.00       11.48     11.0
PH      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   3.0    12.00     11.00     19.00       11.48     11.0
KD      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   1.0    6.00     8.00     22.00       6.86     8.0
PP      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   
LJ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.83
NJ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Average   10.00    10.00    20.00      9.94    30.0
JR      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   W Avg     10.40    10.20    19.80      10.25    30.0
HP      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Test Acc = 0.833

    Модель имеет 100% точность на обучающих данных и 83% точность на данных вне выборки.


    Дерево решений и AI в трейдинге 

    Однако нас интересует конкретная область применения моделей на основе деревьев решений — это трейдинг. Чтобы использовать эту модель в трейдинге, нужно сформулировать проблему, которую надо будет решить.

    Проблема:

    Мы будем использовать ИИ-модель дерева решений, чтобы делать прогнозы на текущем баре относительно того, куда движется рынок: вверх или вниз.

    Как и в случае с любой моделью, мы предоставим нашей модели набор данных для обучения. Для этого будем использовать два индикатора типов осцилляторов: индикатор RSI и стохастический осциллятор. По сути, нам нужно, чтобы модель понимала закономерности между этими двумя индикаторами и то, как они определяют движение цены на текущем баре.

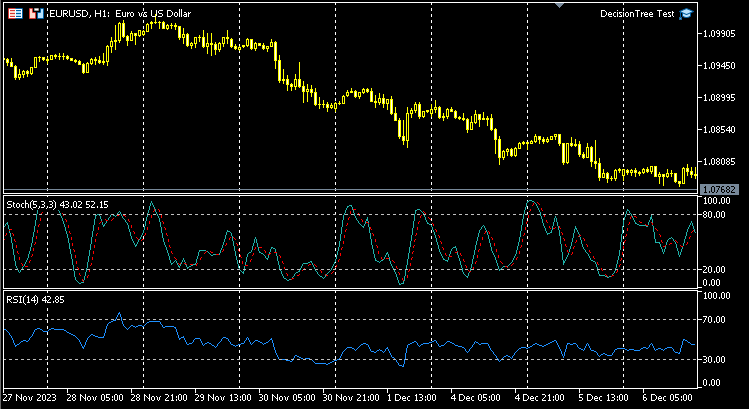
    Структура данных:

    Ниже приведена структура, в которой сохраняются данные, собранные для обучения и тестирования. То же относится и к данным, используемым для прогнозирования в реальном времени.

    struct data{
   vector stoch_buff, 
          signal_buff, 
          rsi_buff, 
          target;
} data_struct;


    Сбор данных, обучение и тестирование дерева решений

    void TrainTree()
 {
  matrix dataset(train_bars, 4);
  vector v;

//--- Collecting indicator buffers

  data_struct.rsi_buff.CopyIndicatorBuffer(rsi_handle, 0, 1, train_bars);
  data_struct.stoch_buff.CopyIndicatorBuffer(stoch_handle, 0, 1, train_bars);
  data_struct.signal_buff.CopyIndicatorBuffer(stoch_handle, 1, 1, train_bars);
  
//--- Preparing the target variable
   
  MqlRates rates[];
  ArraySetAsSeries(rates, true); 
  int size = CopyRates(Symbol(), PERIOD_CURRENT, 1,train_bars, rates);
  
  data_struct.target.Resize(size); //Resize the target vector
  
  for (int i=0; i<size; i++)
    {
      if (rates[i].close > rates[i].open)
        data_struct.target[i] = 1;
      else 
        data_struct.target[i] = -1;
    }
  
  dataset.Col(data_struct.rsi_buff, 0);
  dataset.Col(data_struct.stoch_buff, 1);
  dataset.Col(data_struct.signal_buff, 2);
  dataset.Col(data_struct.target, 3);
   
  decision_tree = new CDecisionTree(min_sample,max_depth_, tree_mode); //Initializing the decision tree
  

  matrix train_x, test_x;
  vector train_y, test_y;
  
  matrix_utils.TrainTestSplitMatrices(dataset, train_x, train_y, test_x, test_y, 0.8, 42); //split the data into training and testing samples

  
  decision_tree.fit(train_x, train_y);  //Building the tree
  decision_tree.print_tree(decision_tree.root); //Printing the tree
  
  vector preds = decision_tree.predict(train_x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(train_y, preds)); //Measuring the accuracy
  
//---

  preds = decision_tree.predict(test_x); //making the predictions on a test data
  
  Print("Test Acc = ",metrics.confusion_matrix(test_y, preds)); //Measuring the accuracy
 }

    Минимальную выборку (параметр min-sample) мы установили в значение 3, а максимальную глубину (max-depth) = 5.

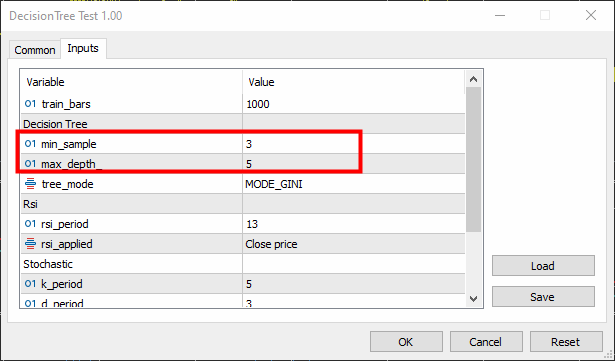
    Результат

    KR      0       16:26:53.028    DecisionTree Test (EURUSD,H1)     : X_0<=65.88930872549261?0.0058610536710859695
CN      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->  left: X_0<=29.19882857713344?0.003187469522387243
FK      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->   left: X_1<=26.851851851853503?0.030198175526895188
RI      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_2<=7.319205739522295?0.040050858232676456
KG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=23.08345903222593?0.04347468770545693
JF      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_0<=21.6795921184317?0.09375
PF      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
ER      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: -1.0
QF      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_2<=3.223853479489069?0.09876543209876543
LH      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
FJ      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
MM      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
MG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->   right: 1.0
HH      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->   right: X_0<=65.4606831930956?0.0030639039663222234
JR      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_0<=31.628407983040333?0.00271101025966336
PS      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=31.20436037455599?0.0944903581267218
DO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_2<=14.629981942657205?0.11111111111111116
EO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: 1.0
IG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: -1.0
EI      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     right: 1.0
LO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->     right: X_0<=32.4469112469684?0.003164795835173595
RO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_1<=76.9736842105244?0.21875
RO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
PG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
MO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_0<=61.82001028403415?0.0024932856070305487
LQ      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
EQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
LE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_2<=84.68660541575225?0.09375
ED      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: -1.0
LM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
NE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->  right: X_0<=85.28191275702572?0.024468404842877933
DK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->   left: X_1<=25.913621262458935?0.01603292204455742
LE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_0<=72.18709160232456?0.2222222222222222
ED      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_1<=15.458937198072245?0.4444444444444444
QQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     left: 1.0
CS      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     right: -1.0
JE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
QM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_0<=69.83504428897093?0.012164425148527835
HP      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=68.39798826749553?0.07844460227272732
DL      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_1<=90.68322981366397?0.06611570247933873
DO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: 1.0
OE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
LI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_1<=88.05704099821516?0.11523809523809525
DE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: 1.0
DM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: -1.0
LG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     right: X_0<=70.41747488780877?0.015360959832756427
OI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     left: 1.0
PI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_0<=70.56490391752676?0.02275277028755862
CF      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
MO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
EG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->   right: X_1<=97.0643939393936?0.10888888888888892
CJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->   left: 1.0
GN      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_0<=90.20261550045987?0.07901234567901233
CP      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=85.94461490761033?0.21333333333333332
HN      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     left: -1.0
GE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_1<=99.66856060606052?0.4444444444444444
GK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
IK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
JM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
KE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Confusion Matrix
DO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   [[122,271]
QF      0       16:26:53.029    DecisionTree Test (EURUSD,H1)    [51,356]]
HS      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
LF      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Classification Report
JR      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
ND      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
GQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   1.0    173.00     393.00     407.00       240.24     393.0
HQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   -1.0    627.00     407.00     393.00       493.60     407.0
PM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
OG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.60
EO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Average   400.00    400.00    400.00      366.92    800.0
GN      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   W Avg     403.97    400.12    399.88      369.14    800.0
LM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Train Acc = 0.598
GK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Confusion Matrix
CQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   [[75,13]
CK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)    [86,26]]
NI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
RP      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Classification Report
HH      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
LR      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
EM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   -1.0    161.00     88.00     112.00       113.80     88.0
NJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   1.0    39.00     112.00     88.00       57.85     112.0
LJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
EL      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.51
RG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Average   100.00    100.00    100.00      85.83    200.0
ID      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   W Avg     92.68    101.44    98.56      82.47    200.0
JJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Test Acc = 0.505

    Модель показала точность 60% во время обучения и 50,5% во время тестирования. Результат, мягко говоря, не очень хороший. Причин может быть много, включая качество данных, которые мы использовали для построения модели, или наличие плохих предикторов. Наиболее распространенной причиной может быть то, что параметры модели были установлены неправильно.

    Чтобы это исправить, нужна настройка параметров, чтобы подобрать наиболее подходящие для конкретных целей параметры. 

    Теперь давайте напишем функцию, которая будет делать прогнозы в реальном времени. 

    int desisionTreeSignal()
 {
//--- Copy the current bar information only

   data_struct.rsi_buff.CopyIndicatorBuffer(rsi_handle, 0, 0, 1);
   data_struct.stoch_buff.CopyIndicatorBuffer(stoch_handle, 0, 0, 1);
   data_struct.signal_buff.CopyIndicatorBuffer(stoch_handle, 1, 0, 1);
   
   x_vars[0] = data_struct.rsi_buff[0];
   x_vars[1] = data_struct.stoch_buff[0];
   x_vars[2] = data_struct.signal_buff[0];
   
   return int(decision_tree.predict(x_vars));
 }

    Будем использовать простую логику для торговли:

    Если дерево решений прогнозирует -1, что означает, что свеча закроется внизу, открываем сделку на продажу. Если оно прогнозирует класс 1, указывающий, что свеча закроется выше, чем открылась, разместить сделку на покупку.

    void OnTick()
  {
//---
    if (!train_once)              // You want to train once during EA lifetime 
      TrainTree();
    train_once = true;
    
    if (isnewBar(PERIOD_CURRENT)) // We want to trade on the bar opening 
      {
        int signal = desisionTreeSignal();
        double min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
        SymbolInfoTick(Symbol(), ticks);
        
         if (signal == -1)
           {
              if (!PosExists(MAGICNUMBER, POSITION_TYPE_SELL)) // If a sell trade doesnt exist
                m_trade.Sell(min_lot, Symbol(), ticks.bid, ticks.bid+stoploss*Point(), ticks.bid - takeprofit*Point());
           }
         else
           {
             if (!PosExists(MAGICNUMBER, POSITION_TYPE_BUY))  // If a buy trade doesnt exist
               m_trade.Buy(min_lot, Symbol(), ticks.ask, ticks.ask-stoploss*Point(), ticks.ask + takeprofit*Point());
           }
      }
  }

    Я провел тестирование на периоде в один месяц с 01.01.2023 по 01.02.2023 по ценам открытия, просто чтобы посмотреть, все ли получится.


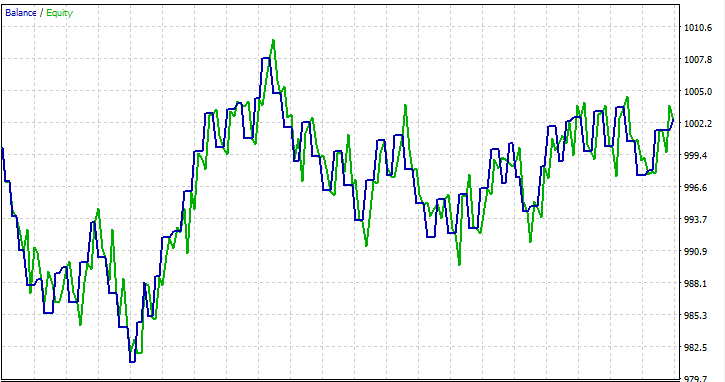
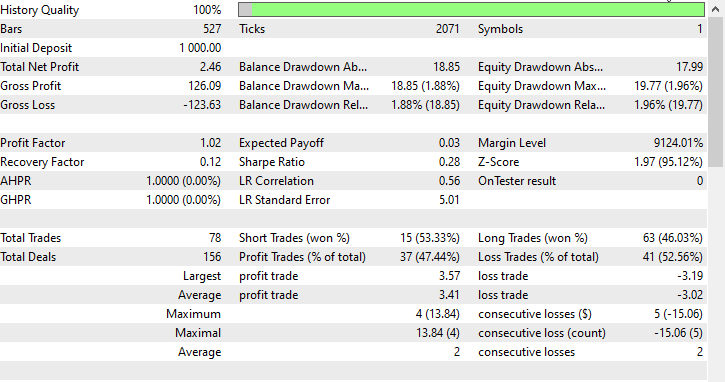
    Часто задаваемые вопросы о деревьях решений в трейдинге:

    Вопрос Ответ
    Важна ли нормализация входных данных для деревьев решений? Нет, нормализация в целом не имеет решающего значения для деревьев решений. Деревья решений разбиваются на основе пороговых значений функций, а масштаб функций не влияет на древовидную структуру. Однако рекомендуется проверять влияние нормализации на производительность модели.
    Как деревья решений обрабатывают категориальные переменные в трейдинговых данных? Деревья решений могут естественным образом обрабатывать категориальные переменные. Они выполняют двоичное разбиение в зависимости от того, выполнено ли условие, включая условия для категориальных переменных. Дерево определит оптимальные точки разделения для категориальных признаков.
    Можно ли использовать деревья решений для прогнозирования временных рядов в трейдинге? Хотя деревья решений можно использовать для прогнозирования временных рядов в трейдинге, они не так эффективно улавливают сложные временные закономерности, как, например, рекуррентные нейронные сети (RNN) и другие подобные модели. При этом ансамблевые методы, такие как случайные леса, могут обеспечить большую надежность.
    Подвержены ли деревья решений проблеме переобучения? Деревья решений, особенно глубокие, могут быть склонны к переобучению из-за шума в обучающих данных. Для предотвращения переобучения в торговых программах можно использовать такие методы, как прореживание и ограничение глубины дерева.
    Подходят ли деревья решений для анализа значимости признаков в торговых моделях? Да, деревья решений обеспечивают естественный способ оценки значимости признаков. Признаки, которые в большей степени способствуют принятию решений о разделении на вершине дерева, обычно более важны. Этот анализ может дать представление о факторах, влияющих на торговые решения.
    Деревья решений чувствительны к выбросам в данных? Деревья решений могут быть чувствительны к ним, особенно если дерево глубокое. Выбросы могут привести к определенным разделениям из-за шума. Для снижения этой чувствительности можно применить этапы предварительной обработки, во время которых такие выбросы обнаруживаются и удаляются.
    Существуют ли конкретные настраиваемые гиперпараметры деревьев решений в торговых моделях?

    Да, ключевые настраиваемые гиперпараметры включают в себя

    • глубина дерева
    • минимальная выборка на лист
    • критерий разделения (например, критерий Джини или энтропия).

    Можно использовать перекрестную проверку, чтобы найти оптимальные значения гиперпараметров для заданных наборов данных.
     Могут ли деревья решений быть частью ансамблевого подхода? Да, деревья решений могут быть частью ансамблевых методов, таких как случайные леса, которые объединяют несколько деревьев для повышения общей эффективности прогнозирования. Ансамблевые методы часто являются надежными и эффективными в приложениях для трейдинга.


    Преимущества деревьев решений:

    Интерпретируемость:

    • Деревья решений легко понять и интерпретировать. Графическое представление древовидной структуры позволяет наглядно визуализировать процессы принятия решений.

    Работа с нелинейностью:

    • Деревья решений могут фиксировать нелинейные связи в данных, что делает их подходящими для решения задач, в которых границы решений не являются линейными.

    Работа со смешанными типами данных:

    • Деревья решений могут принимать как числовые, так и категориальные данные без необходимости серьезной предварительной обработки.

    Значимость признаков:

    • Деревья решений предоставляют естественный способ оценки значимости признаков, помогая выявить критические факторы, влияющие на целевую переменную.

    Не делают допущений относительно распределения данных:

    • Благодаря этому они достаточно универсальны и применимы к различным наборам данных.

    Устойчивость к выбросам:

    • Деревья решений относительно устойчивы к выбросам, поскольку разделения основаны на относительных сравнениях и на них не влияют абсолютные значения.

    Автоматический выбор переменной:

    • Процесс построения дерева включает автоматический выбор переменных, что снижает необходимость ручного подбора признаков.

    Могут обрабатывать отсутствующие значения:

    • Деревья решений могут обрабатывать отсутствующие значения в объектах, не требуя импутации, поскольку разделение производится на основе доступных данных.


    Недостатки деревьев решений:

    Переобучение:

    • Деревья решений склонны к подгонке, особенно если они глубокие и улавливают шум в обучающих данных. Для решения этой проблемы используется, например, прореживание.

    Нестабильность:

    • Небольшие изменения в данных могут привести к значительным изменениям в древовидной структуре, что сделает деревья решений нестабильными.

    Склонность к доминирующим классам:

    • В наборах данных с несбалансированными классами деревья решений могут быть смещены в сторону доминирующего класса, что приводит к неоптимальной производительности для менее представленных классов.

    Глобальное и локальное решение:

    • Деревья решений направлены на поиск локальных оптимальных разбиений в каждом узле, что не обязательно может привести к глобально оптимальному решению.

    Ограниченная выразительность:

    • Деревья решений не всегда справляются с выражением сложных взаимосвязей в данных по сравнению с более сложными моделями, такими как нейронные сети.

    Не подходит для непрерывного вывода:

    • Хотя деревья решений подходят для задач классификации, они не подходят для задач, требующих непрерывного вывода.

    Чувствителен к зашумленным данным:

    • Деревья решений могут быть чувствительны к зашумленным данным, а выбросы могут привести к определенным разделениям, которые основаны на шуме, а не на значимых закономерностях.

    Склонность к доминирующим признакам:

    • Признаки с большим количеством уровней или категорий могут показаться более важными из-за того, как происходит разделение, что потенциально может привести к смещению. Эту проблему можно решить с помощью таких методов, как масштабирование признаков.

    Вот и все, спасибо за внимание.

    Вы можете следить за процессом разработки проекта и вносить свой вклад относительно алгоритма дерева решений и многих других ИИ-моделей в моем репозитории на GitHub: https://github.com/MegaJoctan/MALE5/tree/master

    Содержимое вложения:

    tree.mqh Основной включаемый файл. Код дерева решений, который мы в основном обсуждали в статье.
    metrics.mqh Функции и код для измерения производительности моделей машинного обучения.
    matrix_utils.mqh Дополнительные функции для работы с матрицами.
    preprocessing.mqh Библиотека для предварительной обработки необработанных входных данных, чтобы сделать их пригодными для использования в моделях машинного обучения.
    DecisionTree Test.mq5(EA) Основной файл. Советник для запуска дерева решений.




    Перевод с английского произведен MetaQuotes Ltd.
    Оригинальная статья: https://www.mql5.com/en/articles/13862

    Прикрепленные файлы |
    Загрузить ZIP
    Code.zip (20.2 KB)
    Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

    Другие статьи автора

    Перейти к обсуждению на форуме трейдеров
    Модифицированный советник Grid-Hedge в MQL5 (Часть I): Создание простого хеджирующего советника Модифицированный советник Grid-Hedge в MQL5 (Часть I): Создание простого хеджирующего советника
    Мы будем создавать простой хеджирующий советник в качестве основы для нашего более продвинутого советника Grid-Hedge, который будет представлять собой смесь классической сетки и классических стратегий хеджирования. К концу этой статьи вы узнаете, как создать простую стратегию хеджирования, а также что говорят люди о прибыльности этой стратегии.
    Популяционные алгоритмы оптимизации: Алгоритм боидов, или алгоритм стайного поведения (Boids Algorithm, Boids) Популяционные алгоритмы оптимизации: Алгоритм боидов, или алгоритм стайного поведения (Boids Algorithm, Boids)
    В данной статье мы проводим исследование алгоритма Boids, в основе которого лежат уникальные примеры стайного поведения животных. Алгоритм Boids, в свою очередь, послужил основой для создания целого класса алгоритмов, объединенных под названием "Роевый интеллект".
    Фильтрация и извлечение признаков в частотной области Фильтрация и извлечение признаков в частотной области
    В этой статье мы рассмотрим применение цифровых фильтров к временным рядам, представленным в частотной области, с целью извлечения уникальных признаков, которые могут быть полезными для моделей прогнозирования.
    Парадигмы программирования (Часть 1): Процедурный подход к разработке советника на основе ценовой динамики Парадигмы программирования (Часть 1): Процедурный подход к разработке советника на основе ценовой динамики
    Узнайте о парадигмах программирования и их применении в коде MQL5. В этой статье исследуются особенности процедурного программирования, а также предлагаются практические примеры. Вы узнаете, как разработать советник на основе ценовой динамики (Price Action), используя индикатор EMA и свечные данные. Кроме того, статья знакомит с парадигмой функционального программирования.