Интерпретация моделей: Более глубокое понимание моделей машинного обучения

Введение

В сфере машинного обучения нам часто приходится идти на компромиссы. Оптимизируя один показатель, мы часто ухудшаем другой. По мере создания все более крупных и сложных моделей их понимание, объяснение и отладка становятся всё более сложными задачами. Скрытые особенности модели жизненно важны для расшифровки того, почему наши модели принимают те или иные решения. Без этой ясности как мы можем с уверенностью полагать, что сможем управлять этой моделью для достижения желаемых целей? Мы не можем допустить неправильной работы модели, иначе наши усилия будут тщетными! В статье освещены следующие темы:

1. Определение важнейших особенностей: какие особенности, по мнению пользовательской модели, являются важными.

2. Расшифровка влияния отдельной функции: понимание того, как каждая функция влияет на производительность пользовательской модели.

3. Учет влияния коллективных функций: изучение более широкого влияния функций на прогнозы модели.

Статья раскрывает тонкости машинного обучения, позволяя лучше понимать и изменять поведение модели. Полученные знания позволят вам повысить эффективность ваших усилий при работе с машинным обучением.

Почему это важно?

Отладка:

Рис. 1. Искусство отладки

"Ошибаться — человечно, прощать — божественно" ~ Александр Поуп

На первый взгляд отладка может показаться обыденностью, но ее значение сложно переоценить. Представьте неуловимые ошибки, которые остаются незамеченными на этапе выполнения. Знания, содержащиеся в статье, помогут расшифровать замысловатые узоры, которые ткут ваши модели. Вы поймете, гармонируют ли эти шаблоны с вашим пониманием реального мира. В лабиринте реальных проектов вы сможете умело выслеживать и устранять свои собственные ошибки, нарабатывая необходимый опыт.

Улучшенная разработка функций:

Рис. 2. Разработка функций

"Постоянное совершенствование лучше, чем отсроченное совершенство" ~ Марк Твен

Теперь давайте окунёмся в область разработки функций. Представьте себе круг. Проведите красную линию по его диаметру. Сколько раз ваш диаметр может обогнуть окружность? Ответ напрашивается сам собой – около 3,145. Это константа, известная всем как число Пи.

Этот мысленный эксперимент служит нашим руководством, подчеркивая влияние презентации на нашу способность учиться. Точно так же, как кривизна нашего круга влияет на его форму, так и преобразования объектов улучшают гармонию нашего набора данных. Создавая новые столбцы, мы выходим за рамки обыденности, поднимая точность наших прогнозов на необыкновенную высоту. Здесь интуиция становится нашим компасом, ведущим нас через неизведанные воды. Но что происходит, когда интуиция дает сбой? Не стоит беспокоиться. У нас есть стратегии навигации даже по самым запутанным маршрутам. Но мы не останавливаемся на достигнутом, а продолжаем эмпирически измерять эффективность новых функций.

Управление будущим сбором данных:

Рис. 3. Улучшенный сбор данных

"Если хочешь узнать будущее, загляни в прошлое" ~ Альберт Эйнштейн

При работе с данными следует помнить старую мудрость - ключ к будущему лежит в прошлом. Исчерпаны ли наши возможности по разработке функций? В мире данных прошлое — наш маяк. Новые типы данных манят нас, обещая вдохнуть жизнь в наши модели. Понимание, наш верный спутник, служит посредником, направляя нас к драгоценным камням в сокровищницах данных. С каждым полученным пониманием наш путь к новым функциям становится яснее.

Улучшенное принятие решений:

Рис. 4. Улучшенное принятие решений

"Небольшое обучение — опасная вещь" ~ Александр Поуп

В симфонии машинного обучения дирижером являетесь вы. Модель танцует под вашу дудку, свидетельствуя о решениях, которые вдыхают жизнь в ее прогнозы. Машинное обучение выходит за рамки простых прогнозов. Ваше понимание, ваше мастерство образуют основу, на которой стоят ваши амбиции. Каждое понимание влияет на ваши усилия.

Теория

В этой статье наша цель — использовать древовидную модель с градиентным усилением (gradient boosted tree model), доступную в библиотеке CatBoost Python, для проведения ценового регрессионного анализа. Однако с самого начала возникает примечательная проблема, требующая более тщательного изучения модели. Прежде чем углубляться в применение методов объяснения "черного ящика" для нашей модели, необходимо осознать ограничения, присущие нашей модели "черного ящика", и обоснование блока объяснений (explainers) "черного ящика" в этом контексте.

Деревья с градиентным усилением демонстрируют хорошую производительность в задачах классификации. Тем не менее, они демонстрируют явные ограничения при применении к конкретным задачам регрессии временных рядов. Эти деревья, принадлежащие к семейству моделей машинного обучения, классифицируют входные данные по группам в зависимости от целевого значения. Впоследствии алгоритм вычисляет среднее целевое значение внутри каждой группы и использует эти средние значения группы для прогнозирования. Примечательно, что эти средние значения по группе, установленные во время обучения, остаются неизменными, пока не будет проведено дальнейшее обучение. Из этой фиксированной природы вытекает критический недостаток, поскольку деревьям с усилением градиента обычно сложно эффективно экстраполировать тренды. Когда модель сталкивается с входными значениями за пределами области обучения, она склонна к повторяющимся прогнозам, полагаясь на средние значения, полученные из известных групп, которые могут неточно отражать основную тенденцию за пределами наблюдаемого диапазона обучения.

Более того, модель предполагает, что схожие значения характеристик приведут к схожим целевым значениям, что противоречит нашему коллективному опыту торговли финансовыми инструментами. На финансовых рынках ценовые модели могут проявлять сходство, хотя и завершаются в разных точках. Это расхождение бросает вызов предположению модели о том, что генеративный процесс производит данные, попадающие в однородные группы. Следовательно, нарушение этих предположений вносит предвзятость в нашу модель.

Чтобы обосновать эти наблюдения, мы проведем демонстрацию для читателей, которые, возможно, не наблюдали самостоятельно это явление. Наша цель – обеспечить всестороннее понимание для всех читателей.

Начинаем с загрузки необходимых зависимостей

#pip install pandas if you haven't installed it allready
#We'll use pandas to store and retrieve data
import pandas as pd       

#pip install pandas-ta if you haven't installed it allready
#We'll use pandas_ta to calculate technical indicators
import pandas_ta as ta    

#pip install numpy if you haven't installed it allready
#We'll use numpy to perform optmized vector calculations 
import numpy as np

import matplotlib.pyplot as plt

#pip install numpy if you haven't installed it allready
#We'll use MetaTrader 5 connect to and control our MetaTrader 5 Terminal 
import MetaTrader5 as MT5

#Standard python library
import time

Затем вводим наши учетные данные для входа

login = enter_your_login
password =  enter_your_password
server = enter_your_broker_server

Инициализируем наш терминал MetaTrader 5 и авторизуемся.

if(MT5.initialize(login=login, password= password, server=server)):
    print("Logged in succesfully")
else:
    print("Failed to initialize the terminal and login")

Авторизация успешна

Давайте запросим миллион строк данных M1 по индексу волатильности 75 или любому другому символу, который вы предпочитаете.

data = pd.DataFrame(MT5.copy_rates_from_pos("Volatility 75 Index",MT5.TIMEFRAME_M1,0,100000))
data

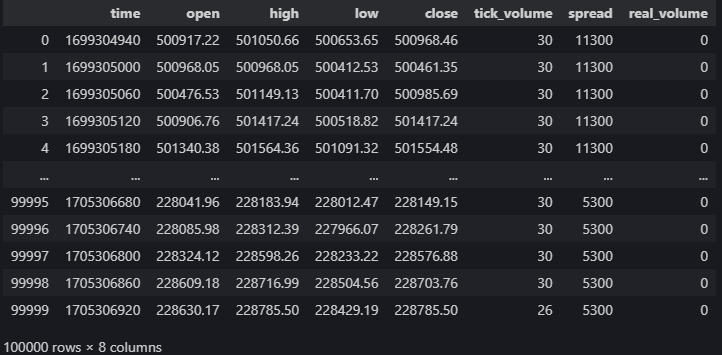
Рис. 5. Наши рыночные данные из терминала MetaTrader 5

Рассчитаем технические индикаторы, которые могут помочь нам спрогнозировать цену.

#20 period exponential moving average
data["ema_20"] = data.ta.ema(length=20)
#40 period exponential moving average
data["ema_40"] = data.ta.ema(length=40)
#100 period exponential moving average
data["ema_100"] = data.ta.ema(length=100)
#20 period relative strength indicator
data.ta.rsi(length=20,append=True)
#20 period bollinger bands with 3 standard deviations
data.ta.bbands(length=20,sd=3,append=True)
#14 period average true range
data.ta.atr(length=14,append=True)
#Awesome oscilator with default settings
data.ta.ao(append=True)
#Moving average convergence divergence (MACD)
data.ta.macd(append=True)
#Chaikins commidity index
data.ta.cci(append=True)
#Know sure thing oscilator
data.ta.kst(append=True)
#True strength index
data.ta.tsi(append=True)
#Rate of change
data.ta.roc(append=True)
#Slope between 2 points
data.ta.slope(append=True)
#Directional movement
data.ta.dm(append=True)

Настройка цели

data["target"] = data["close"].shift(-30)

Настроим нашу модель черного ящика

from catboost import CatBoostRegressor

Подготовка обучения и тестовых сплитов

train_start = 100
train_end   = 10000

test_start = train_end + 100
test_end = test_start + 30000

predictors = [
    "open",
    "high",
    "low",
    "close",
    "KSTs_9",
    "KST_10_15_20_30_10_10_10_15",
    "CCI_14_0.015",
    "AO_5_34",
    "ATRr_14",
    "BBM_20_2.0",
    "BBP_20_2.0",
    "BBB_20_2.0",
    "BBU_20_2.0",
    "BBL_20_2.0",
    "RSI_20",
    "ema_20",
    "ema_40",
    "ema_100",
    "SLOPE_1",
    "ROC_10",
    "TSIs_13_25_13",
    "TSI_13_25_13",
    "MACD_12_26_9",
    "MACDh_12_26_9",
    "MACDs_12_26_9",
    "DMP_14",
    "DMN_14"
]
target = "target"

Деревья решений чувствительны к масштабу, поэтому мы нормализуем входные значения и будем хранить первые показания каждого объекта в этом массиве под названием first_values.

first_values = {}

#Iterating over the columns in the dataset
for col in data.columns:
    #Which of those columns are part of the model inputs?
    if col in predictors:
        #What was the first value in that column?
        first_values[col] = data[col][train_start]
        data[col] = data[col]/first_values[col]

Выполнение тестового сплита Train

train_x = data.loc[train_start:train_end,predictors]
train_y = data.loc[train_start:train_end,target]

test_x = data.loc[test_start:test_end,predictors]
test_y = data.loc[test_start:test_end,target]

Установка нашей модели черного ящика

cat_full = CatBoostRegressor()
cat_full.fit(train_x,train_y)

Получение прогнозов из нашей модели черного ящика

cat_full_predictions = pd.DataFrame(index=test_x.index)
cat_full_predictions["predictions"] = cat_full.predict(test_x)
cat_full_predictions.plot(label=True)
test_y.plot()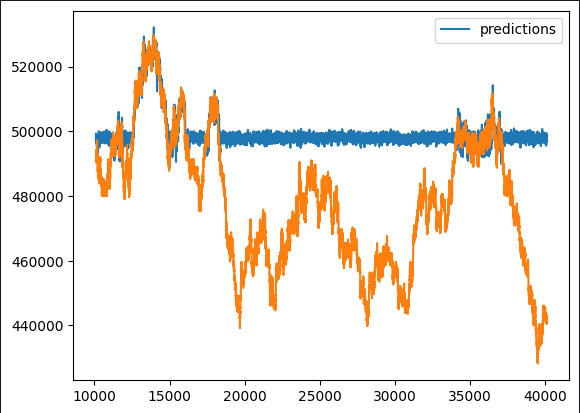

Рис. 6. Прогноз нашего "черного ящика"

При первоначальном наблюдении становится очевидным, что прогнозная модель демонстрирует нетипичные плоские периоды. Учитывая наш всесторонний обзор типичной реализации алгоритмов с градиентным усилением, такие закономерности вполне ожидаемы. Мы хотим выяснить, какие функции положительно влияют на производительность нашей модели, а какие могут служить потенциальными источниками шума. Это требует тщательного изучения возможностей проектирования функций.

Чтобы раскрыть эти нюансы, мы предлагаем использовать блок объяснений "черного ящика". Однако прежде чем слепо применять эти объяснения, необходимо понять основные механизмы алгоритма блока объяснения "черного ящика". Это предполагает критическую оценку предположений, в соответствии с которыми он действует, что позволяет нам установить, соблюдаются ли эти предположения или они потенциально нарушаются.

Подход к применению техник объяснения "черного ящика" с учетом этого основополагающего понимания позволяет нам разумно интерпретировать каждое объяснение. Тщательно исследуя методы объяснения и взвешивая их актуальность, мы можем приписать соответствующие уровни уверенности полученным открытиям. Этот методический подход расширяет нашу способность извлекать значимую информацию и принимать обоснованные решения на основе результатов процесса объяснения "черного ящика".

Алгоритмы объяснения черного ящика

Важность удаления столбца (Drop Column Importance):

Метод важности удаления столбца используется для оценки точности модели путем первоначального рассмотрения всех предикторов, а затем итеративного удаления одного столбца с учетом результирующего влияния на точность. Этот подход дает ценную информацию о конкретном вкладе каждого столбца в общую производительность модели.

Метод отличается практичностью и разумностью. Предположение, лежащее в основе этого метода, соответствует реальным сценариям, в которых часто возникает несогласованность данных. Независимо от того, вызвана ли она перебоями в подключении к Интернету, перебоями в подаче электроэнергии, неблагоприятными погодными условиями или другими непредвиденными событиями, методология имитирует надежную модель, которая отражает события в реальной операционной среде. Этот реализм повышает применимость и эффективность метода при рассмотрении сценариев, с которыми можно столкнуться в практических повседневных ситуациях.

Преимущества:

• Улучшенная производительность модели: удаление ненужных или избыточных столбцов может повысить производительность моделей машинного обучения за счет снижения шума и улучшения соотношения "сигнал/шум".
• Упрощенная модель: удаление ненужных столбцов может привести к созданию более простых и интерпретируемых моделей, что облегчит их понимание и объяснение заинтересованным сторонам.

Недостатки:

• Потеря информации: удаление столбца может привести к потере ценной информации, что потенциально может привести к созданию чрезмерно упрощенной модели, которая не сможет отразить важные закономерности в данных.
• Влияние на последующие процессы: если столбец используется в последующих анализах или необходим для определенных бизнес-процессов, его удаление может нарушить эти рабочие процессы.

Возможности:

• Разработка функций: удаление столбца может предоставить возможность для разработки функций, позволяя создавать новые функции на основе существующих данных или изменять оставшиеся функции для повышения производительности модели.
• Оптимизация ресурсов: удаление ненужных столбцов может привести к экономии ресурсов с точки зрения памяти, хранилища и времени обработки, особенно в больших наборах данных.

Потенциальные проблемы:

• Смещение модели: если удаленный столбец содержит информацию, важную для объективных прогнозов, его удаление может привести к смещению модели, что приведет к неточным результатам.
• Проблема целостности данных: удаление столбцов без полного понимания данных может привести к проблемам с целостностью, что повлияет на общее качество набора данных и последующий анализ.

Важность перестановки (Permutation Importance):

Важность перестановки предлагает альтернативный метод оценки важности функции путем случайной перестановки значений определенного столбца и оценки результирующего влияния на показатели ошибок модели. Основная идея основана на предположении, что если столбец играет существенную роль во влиянии на модель, нарушение его исходных значений должно привести к увеличению показателей ошибок и снижению общей точности. И наоборот, если влияние столбца минимально, наблюдаемые изменения будут ограничены, а в некоторых случаях может даже наблюдаться улучшение производительности.

Этот метод обеспечивает детальный взгляд на важность признаков, позволяя динамически оценивать вклад каждого признака в прогностическую способность модели. Процесс перестановки вводит уровень случайности, который помогает выявить чувствительность модели к отдельным функциям, позволяя более полно понять их значение в системе прогнозирования.

Преимущества:

• Независимость от модели: важность перестановки не зависит от модели, то есть ее можно применять к любой модели обучения с учителем без предположений о базовом алгоритме. Это делает его универсальным и широко применимым методом.
• Интуитивная интерпретация: концепцию важности перестановок относительно легко понять. Она измеряет изменение производительности модели, когда значения конкретного признака переставляются случайным образом, обеспечивая четкую интерпретацию важности признака.

Недостатки:

• Интенсивность вычислений: расчет важности перестановок включает в себя повторную оценку производительности модели для каждой перестановки признаков, что делает его вычислительно интенсивным и потенциально трудоемким, особенно для больших наборов данных.
• Чувствительность к размеру выборки: важность перестановки может зависеть от размера набора данных. В небольших наборах данных влияние перестановки объекта может быть преувеличено, что приведет к менее надежным оценкам важности.

Возможности:

• Руководство по выбору функций: результаты важности перестановок могут помочь в выборе функций, определяя, какие функции больше всего влияют на производительность модели. Эта информация может быть полезна для упрощения моделей и уменьшения размерности.
• Идентификация нелинейных связей: в отличие от линейных моделей, важность перестановок может отражать нелинейные связи между признаками и целевой переменной, обеспечивая понимание сложных закономерностей в данных.

Потенциальные проблемы:

• Влияние коррелированных функций: важность перестановки может плохо справляться с ситуациями, когда функции сильно коррелируют. Если две функции коррелируют, перестановка одной из них может незначительно повлиять на производительность модели, если другая функция по-прежнему предоставляет аналогичную информацию.
• Возможность переобучения: в некоторых случаях существует риск переобучения (подгонки), особенно если модель слишком сложна или если набор данных небольшой. Оценки важности могут плохо обобщаться на новых данных.

Графики частичной зависимости (Partial Dependence Plots, PDP) и индивидуального условного ожидания (Individual Conditional Expectation, ICE):

Графики позволяют получить более детальное понимание поведения модели. Графики частичной зависимости иллюстрируют, как прогнозируемый результат развивается по мере изменения одного предиктора, сохраняя при этом все остальные предикторы постоянными. Между тем, графики ICE дают подробное представление о важности функций, представляя отдельные кривые для каждого экземпляра, что облегчает всесторонний анализ влияния каждой функции.

Вместе PDP и ICE Plots предлагают надежное визуальное представление, выходящее за рамки совокупных тенденций. Графики PDP предоставляют комплексное представление о взаимосвязи между конкретным предиктором и прогнозами модели, а графики ICE углубляются в нюансы, представляя набор кривых, каждая из которых представляет индивидуальное влияние этого предиктора в разных случаях. Этот комбинированный подход расширяет нашу способность различать сложные закономерности и вариации реакции модели на различные значения предикторов, способствуя более глубокому пониманию важности функций в общей системе прогнозирования.

Преимущества:

• Интерпретируемость: PDP обеспечивают интуитивное и визуальное представление взаимосвязи между функцией и прогнозируемым результатом, что облегчает неспециалистам интерпретацию и понимание влияния конкретной функции на прогнозы модели.
• Выявление закономерностей: PDP могут помочь выявить закономерности и тенденции во взаимосвязи между признаком и прогнозируемым результатом, позволяя глубже понять, как изменения признака влияют на прогнозы модели.

Недостатки:

• Допущение независимости: PDP предполагают, что интересующая функция не зависит от других функций. В сложных моделях с коррелирующими характеристиками интерпретация PDP может быть сложной, а графики могут неточно отражать истинные взаимосвязи.
• Ограниченность предельным эффектом: PDP показывают предельный эффект одной функции, сохраняя при этом другие функции фиксированными. Они могут не отражать сложные взаимодействия между несколькими функциями, что ограничивает их способность раскрыть всю сложность модели.

Возможности:

• Проверка модели: PDP можно использовать в качестве инструмента проверки модели. Сравнивая информацию, полученную в ходе PDP, со знаниями или ожиданиями предметной области, специалисты-практики могут оценить, соответствует ли модель ожидаемому поведению функций.
• Ранжирование важности функций: PDP могут помочь в ранжировании важности функций, визуально выделяя функции, которые оказывают наиболее существенное влияние на прогнозы модели. Эта информация может помочь в выборе функций и упрощении модели.

Потенциальные проблемы:

• Возможность неправильной интерпретации: без надлежащего понимания статистических концепций существует риск неправильного толкования. Пользователи могут ошибочно приписать причинно-следственные отношения наблюдаемым связям, особенно если они не знают о потенциальных искажающих переменных или основных сложностях модели.
• Сложность многомерных данных: PDP становится сложно интерпретировать в многомерных пространствах из-за комбинаторного взрыва возможных комбинаций функций. Визуализация взаимодействия между функциями становится все более сложной.

Значения SHAP (Shapley Additive Explanations, аддитивные объяснения Шепли):

Рис. 7. Светлой памяти Ллойда Шепли, скончавшегося 12 марта 2016 года в городе Тусон, штат Аризона. Его идеи будут жить вечно

Значения SHAP, названные в честь их первооткрывателя Ллойда Шепли, используются для объяснения результатов модели путем определения вклада каждого признака в прогноз.

Значения SHAP можно вычислить, оценив выходные данные модели для всех возможных комбинаций функций. Проще говоря, они включают в себя перетасовку значений определенного признака, сохраняя при этом остальные постоянными и наблюдая за влиянием на прогнозы модели.

Подобно игроку, если функция постоянно не меняет выходные данные модели при перетасовке ее значения (например, игрок, не влияющий на производительность команды, когда он не участвует), значение SHAP для этой функции имеет тенденцию быть ниже. Напротив, если изменение признака существенно влияет на выходные данные модели, значение SHAP будет выше, что указывает на более существенный вклад.

Значения SHAP дают количественную оценку вклада каждой функции. Сравнивая значения SHAP для разных объектов, мы можем сделать вывод о том, какие функции оказывают более существенное влияние на прогнозы модели.

Таким образом, если какой-либо признак неоднократно игнорируется (его значения перемешиваются или изменяются), а производительность модели существенно не меняется, это означает, что вклад этого признака в прогнозы модели может быть относительно небольшим.

Преимущества:

• Независимость от модели: значения SHAP не зависят от модели, то есть их можно применять к любой модели машинного обучения, включая сложные модели, такие как ансамблевые методы, нейронные сети и машины опорных векторов (support vector machines).
• Глобальная и локальная интерпретируемость: значения SHAP обеспечивают как глобальную, так и локальную интерпретируемость. Они могут объяснить влияние отдельных функций на конкретный прогноз (локальная интерпретируемость) и общий вклад каждой функции во весь набор данных (глобальная интерпретируемость).

Недостатки:

• Интенсивность вычислений: вычисление значений SHAP может потребовать больших вычислительных ресурсов, особенно для больших наборов данных или сложных моделей. Это может создавать проблемы в приложениях реального времени или в ситуациях, когда вычислительные ресурсы ограничены.
• Проблемы интерпретации многомерных данных: интерпретация значений SHAP для моделей с большим количеством функций может оказаться сложной задачей. Визуализация и понимание вклада многочисленных функций становится более сложной задачей в многомерных пространствах.

Возможности:

• Ранжирование важности объектов: значения SHAP можно использовать для ранжирования объектов на основе их влияния на прогнозы модели. Эта информация полезна для выбора функций и определения наиболее влиятельных переменных в модели.
• Пояснительные визуализации: значения SHAP позволяют создавать подробные визуализации, такие как сводные графики SHAP или графики отдельных сил, помогая передавать прогнозы модели и информацию о характеристиках заинтересованным сторонам.

Потенциальные проблемы:

• Допущение согласованности: значения SHAP предполагают согласованность, что означает, что влияние функции на прогноз одинаково в разных экземплярах. В некоторых случаях это допущение может не выполняться, что приводит к потенциальным неверным интерпретациям.
• Сложность интерпретации: хотя значения SHAP дают ценную информацию, их правильная интерпретация требует четкого понимания основных концепций. Пользователи могут неправильно истолковать значение определенных значений или не уловить нюансы вклада тех или иных функций.

Взаимная информация (Mutual Information, MI):

Взаимная информация — это мера количества информации, которую наличие или отсутствие одной переменной дает о другой переменной. Она количественно определяет степень зависимости или связи между двумя переменными.

Преимущества:

• Независимость от модели: взаимная информация не зависит от конкретной модели машинного обучения. Ее можно применять к любому типу связей между переменными, включая как линейные, так и нелинейные зависимости.
• Фиксирует нелинейные связи: в отличие от корреляции, которая больше подходит для линейных связей, взаимная информация может фиксировать нелинейные зависимости между переменными, что делает ее универсальной для различных типов данных.

Недостатки:

• Чувствительность к размеру выборки: взаимная информация может быть чувствительна к размеру набора данных. В небольших наборах данных оценка MI может быть менее стабильной, а небольшие изменения в данных могут оказать более существенное влияние на результаты.
• Сложность интерпретации величины: хотя MI обеспечивает меру силы ассоциации, ее абсолютные значения могут быть сложны для прямой интерпретации. Интерпретация "высокой" или "низкой" взаимной информации зависит от контекста и масштаба переменных.

Возможности:

• Выбор функций: взаимная информация может использоваться для выбора функций путем ранжирования функций на основе их релевантности целевой переменной. Функции с более высокими значениями MI считаются более информативными для прогнозирования цели.
• Важность переменных в ансамблевых моделях: при ансамблевом обучении взаимная информация может использоваться для оценки важности переменных, помогая в построении более точных и интерпретируемых ансамблевых моделей.

Потенциальные проблемы:

• Допущение независимости: взаимная информация предполагает, что переменные независимы, когда их MI равна нулю. На практике она может не отражать сложные зависимости или отношения, на которые влияют скрытые факторы или мешающие переменные.
• Интенсивные вычисления для больших размерностей: оценка взаимной информации для многомерных данных может потребовать больших вычислительных ресурсов. Это может создать проблемы с точки зрения необходимого времени и ресурсов.

К счастью, специализированные библиотеки Python упрощают этот процесс, избавляя нас от необходимости создавать большую часть кода с нуля.

В этой статье мы не будем углубляться в тонкости обучения и подбора моделей. Вместо этого мы сосредоточимся на последующем после обучения этапе и рассмотрим, как оценивать и интерпретировать производительность модели. В приведенном примере кода базовая модель строится исключительно в иллюстративных целях, демонстрируя шаги, предпринятые после проектирования и обучения модели. 

Давайте начнем 

Важность удаления столбца

Мы будем использовать алгоритм исключения рекурсивных функций (Recursive Feature Elimination algorithm) из библиотеки sklearn, который будет служить реализацией важности удаления столбца.

from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR

Алгоритм рекурсивного исключения функций ожидает, что мы предоставим модель обучения с учителем, которую он сможет вместить и оценить.
Модель должна предоставлять информацию о важности признака либо через коэффициенты, либо через специальную функцию.
Модель не обязательно должна быть такой же, как модель, которую мы используем в нашей задаче.
Модель не обязательно должна быть из библиотеки sklearn, но она должна иметь как минимум обертку sklearn.

Мы будем использовать линейную модель и оценивать ее точность, случайным образом удаляя функции.

lm = LinearRegression()

rfe = RFE(lm,step=1)

Аргумент шага указывает, сколько объектов следует удалить на каждой итерации.

Затем мы устанавливаем алгоритм рекурсивного исключения функций

rfe = rfe.fit(train_x,train_y)

Давайте проверим, какие функции наш алгоритм RFE посчитал информативными

rfe.support_

array([ True, True, True, True, False, False, False, False, False, True, False, True, True, True, False, True, True, True, False, False, False, False, False, False, True, False, True])

Мы также можем получить рейтинг каждой функции

rfe.ranking_

array([ 1, 1, 1, 1, 2, 5, 14, 11, 13, 1, 7, 1, 1, 1, 8, 1, 1, 1, 12, 15, 3, 4, 9, 10, 1, 6, 1])

Реализация sklearn предоставляет нам маску, которую мы можем применить к столбцам в нашем кадре данных train_x, чтобы увидеть имена столбцов, которые RFE считает важными.

train_x.columns[rfe.support_]

Index(['open', 'high', 'low', 'close', 'BBM_20_2.0', 'BBB_20_2.0', 'BBU_20_2.0', 'BBL_20_2.0', 'ema_20', 'ema_40', 'ema_100', 'MACDs_12_26_9', 'DMN_14'], dtype='object')

Итак, из всех примененных нами индикаторов видно, что следующие из них содержат ценную информацию:
    1)Open         2)High         3)Low         4)Close         6)KSTs_9         7)KST_10_15_20_30_10_10_10_15         7)Все 3 экспоненциальные скользящие средние         8)4 Компоненты полосы Боллинджера: 'BBM_20_2.0' 'BBB_20_2.0' 'BBU_20_2.0' 'BBL_20_2.0'         9)MACD: 'MACDs_12_26_9'         10)Направленное движение отрицательное     Другие индикаторы, возможно, вносили шум, но помните, что это!
Мы не можем заключить, что это именно так, однако для нас это все же разумное утверждение.

Далее мы переходим к оценке важности перестановки

Для реализации алгоритма мы будем использовать библиотеку Python под названием Explain Like I'm 5 (ELI5) - "Объясни, как будто мне 5"

#pip install eli5 if you don't allready have it installed
import eli5
from eli5.sklearn import PermutationImportance
from sklearn.ensemble import GradientBoostingRegressor

gbr = GradientBoostingRegressor().fit(train_x,train_y)

permutation = PermutationImportance(gbr).fit(test_x,test_y)

Теперь мы оценим веса, которые алгоритм присвоил каждой из наших функций.

eli5.show_weights(permutation,feature_names = test_x.columns.to_list())

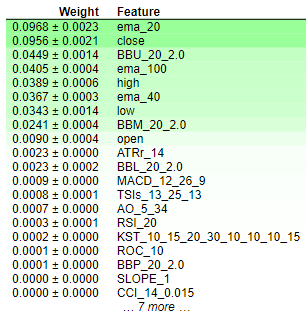
Рис. 8. Веса важности перестановок

Интерпретация результатов важности перестановок довольно проста. Функции ранжированы в порядке убывания важности: наиболее важные расположены вверху, а менее значимые — внизу. Значение веса (например, "0.0986 +- 0.0256") означает изменение показателей ошибки модели. Если коротко, важность перестановки предполагает случайное перетасовывание значений признака. Если функция существенно влияет на модель, эта рандомизация должна привести к увеличению показателей ошибок модели. Из-за стохастической природы алгоритма это увеличение представлено в виде диапазона, а не конкретного значения.

И наоборот, для функций, которые не являются важными, не будет никаких изменений или, в некоторых случаях, уменьшения показателей ошибок модели, когда значения перетасовываются случайным образом. Этот двойственный характер результатов — либо увеличение, либо уменьшение показателей ошибок — обеспечивает четкое указание относительной важности каждой функции, способствуя краткой и понятной интерпретации результатов важности перестановок. Таким образом, мы можем заключить, что важность удаления столбца и важность перестановки имеют схожие "мнения" относительно важности функций в нашей модели.

Графики частичной зависимости (PDP) и индивидуального условного ожидания (ICE):

#Import partial dependence display from sklearn
from sklearn.inspection import PartialDependenceDisplay

for feature_name in predictors:
    PartialDependenceDisplay.from_estimator(cat_full,test_x,[feature_name])
    plt.grid()
    plt.show()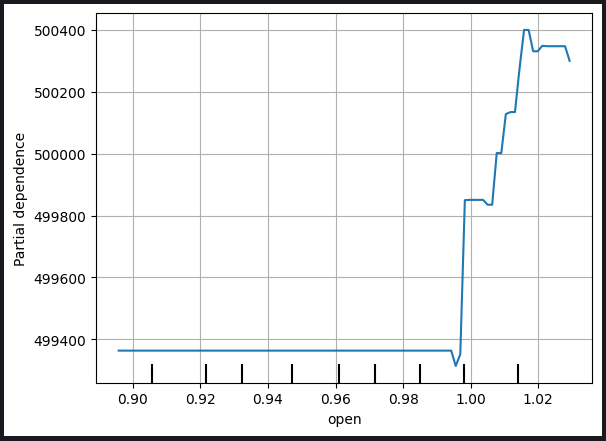

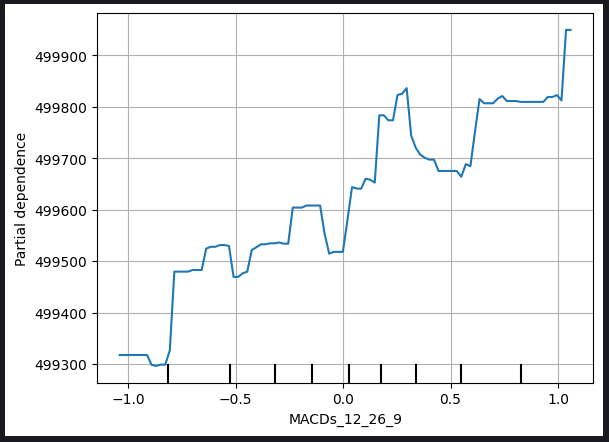
Рис. 9. График частичной зависимости цены открытия и сигнальной линии MACD

График частичной зависимости служит ценным инструментом для понимания того, как изменение конкретной переменной влияет на прогнозы нашей модели. Анализируя график частичной зависимости сигнальной линии MACD, мы можем обоснованно сделать вывод, что в целом увеличение сигнальной линии MACD связано с ростом прогнозируемой нами цены закрытия нашей модели.

Однако интерпретация графиков частичной зависимости может быть более сложной, как показано на графике высоты MACD (MACD Height) ниже.

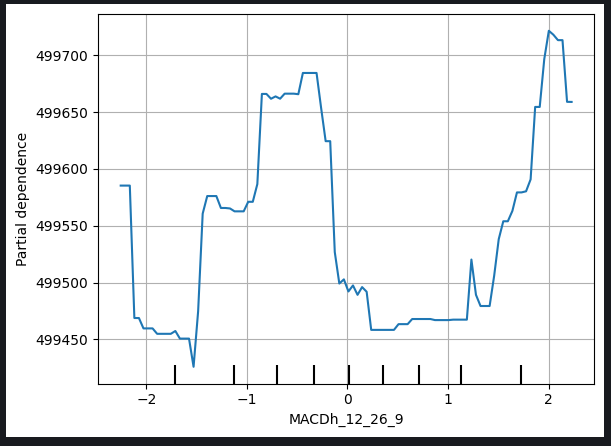
Рис. 10. График частичной зависимости высоты MACD

Сложности в интерпретации таких графиков могут возникнуть из-за нелинейных связей или взаимодействия с другими переменными, которые требуют более детального анализа. В случае графика высоты MACD могут потребоваться дополнительные соображения и исследования, чтобы выявить точный характер взаимосвязи между высотой MACD и прогнозируемой ценой закрытия модели.

Это признание подчеркивает необходимость всестороннего изучения графиков частичной зависимости с учетом уникальных характеристик каждой переменной и, при возникновении проблем с интерпретацией, поиска дополнительной информации посредством дополнительного анализа или консультаций со специалистами.

Графики индивидуальных условных ожиданий (ICE) создаются для предоставления детального представления о том, как отдельные экземпляры реагируют на изменения конкретной переменной предиктора. Ниже представлено пошаговое объяснение того, как создаются и используются графики ICE:

1. Индивидуальные варианты прогнозов:

• Начнем с набора данных, содержащего интересующую нас переменную-предиктор и другие необходимые функции.
• Выберите конкретный экземпляр из набора данных.

2. Изменим переменную-предиктор:

• Для выбранного экземпляра систематически изменяйте значения переменной-предиктора, сохраняя при этом другие характеристики постоянными.
• Создайте набор прогнозов, соответствующий каждому значению переменной-предиктора.

3. Создадим отдельные кривые:

• Повторите шаги 1–2 для нескольких экземпляров в наборе данных, создав набор отдельных кривых (по одной для каждого экземпляра), которые иллюстрируют взаимосвязь между переменной-предиктором и прогнозами модели.

4. Отрисовка:

• Постройте каждую отдельную кривую на одном графике. Ось X представляет значения переменной-предиктора, а ось Y представляет прогнозы модели.

5. Интерпретация:

• Проанализируйте график ICE, чтобы наблюдать, как прогнозы модели изменяются для каждого экземпляра при изменении переменной-предиктора.
• Определите закономерности, тенденции или вариации кривых, чтобы получить представление о влиянии переменной-предиктора на отдельные прогнозы.

6. Сравнительный анализ:

• Сравните несколько графиков ICE, особенно при работе с разными экземплярами, чтобы понять неоднородность влияния переменной на набор данных.

Использование:

• Детальное понимание: Графики ICE предлагают подробное, конкретное представление о том, как переменная-предиктор влияет на прогнозы, что позволяет получить более детальное понимание.
• Понимание модели: Графики помогают пользователям исследовать нелинейные отношения, взаимодействия и потенциальные аномалии, которые могут быть не очевидны в совокупных представлениях.
• Важность функций: Графики ICE могут способствовать оценке важности конкретной особенности, иллюстрируя ее влияние на отдельные прогнозы.
• Поддержка решения: Информация из графиков ICE может помочь в принятии решений, особенно когда важно понять, как прогнозы меняются для конкретных случаев в ответ на изменения конкретной переменной.

На самом деле график PDP — это просто среднее значение построенных графиков ICE. Линия PDP показана оранжевым цветом ниже.

for feature in predictors:
    PartialDependenceDisplay.from_estimator(cat_full,test_x,[feature],kind='both')

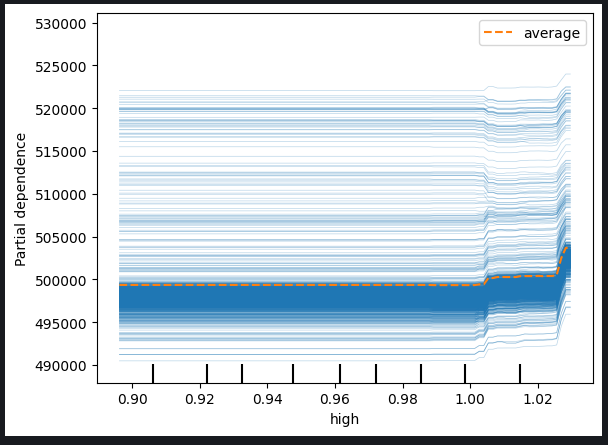
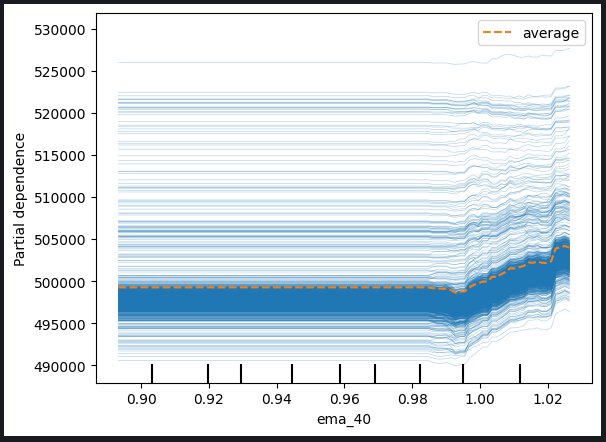
Рис. 11. График ICE с высокой ценой и EMA с периодом 40

Судя по наблюдаемым графикам, очевидно, что увеличение либо высокой цены, либо экспоненциальной скользящей средней не приводит к немедленному влиянию на прогнозы нашей модели. Вместо этого, похоже, что эти переменные должны будут значительно увеличиться, прежде чем можно будет ожидать каких-либо заметных изменений в прогнозах модели. Это наблюдение предполагает, что модель не очень чувствительна к постепенным изменениям этих конкретных характеристик.

Ключевые выводы, полученные на основе графиков:

1. Пороговая чувствительность: Модель, похоже, демонстрирует пороговую чувствительность, а это означает, что ей требуется существенный или пороговый уровень изменения высокой цены или экспоненциальной скользящей средней, прежде чем она существенно скорректирует свои прогнозы.

2. Постепенный ответ: Постепенные или умеренные изменения упомянутых характеристик, похоже, не приводят к немедленным корректировкам прогнозов модели. Эта характеристика предполагает постепенную или сдержанную реакцию на такие изменения.

3. Низкая чувствительность: Вывод о том, что модель не очень чувствительна к изменениям этих характеристик, подразумевает, что незначительные колебания высокой цены или экспоненциальной скользящей средней вряд ли окажут заметное влияние на результаты модели.

Понимание чувствительности модели к различным функциям имеет решающее значение для эффективной интерпретации модели и принятия решений. Эти идеи могут помочь в дальнейшем анализе, совершенствовании модели или информировать заинтересованные стороны о характере взаимосвязей между конкретными предикторами и прогнозами модели.

Мы также можем проверить двухмерные графики частичной зависимости, чтобы увидеть совместный эффект двух функций.

#Setting up the plot
fig , ax = plt.subplots(figsize=(10,5))
column_names = [('ROC_10','ATRr_14')]

#Plotting 2D PDP
disp_4 = PartialDependenceDisplay.from_estimator(cat_full, test_x[0:1000],column_names, ax=ax)
plt.show()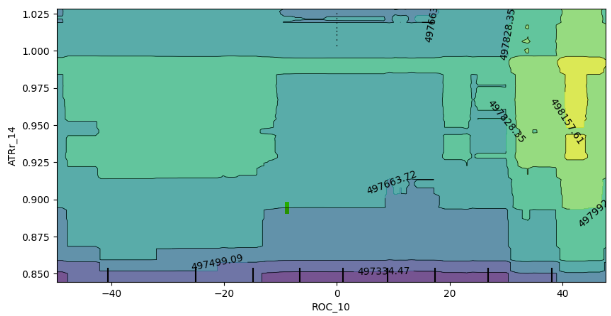

Рис. 12. 2D-график частичной зависимости индикатора скорости изменения (ROC) и среднего истинного диапазона (ATR)

Анализ графика частичной зависимости 2D показывает, что в целом увеличение показателей ROC (скорость изменения) и ATR (средний истинный диапазон) соответствует увеличению ожидаемого прогноза нашей модели. Эта положительная корреляция согласуется с ожидаемым поведением модели в ответ на изменения этих показателей.

Однако график также дает представление о взаимодействии этих двух показателей. Примечательно, что отсутствие четко определенных границ на графике предполагает, что отношения не всегда стабильны. Вместо этого существуют области смешанной силы и слабости, что указывает на то, что влияние индикаторов ROC и ATR на прогнозы модели может различаться в разных областях графика.

Наличие случайных анклавов слабых ожиданий внутри границ сильных ожиданий еще больше подчеркивает динамичный характер взаимодействия. Важно отметить, что на наблюдаемое поведение может влиять метод выборки, особенно если подмножество кадра данных использовалось из соображений эффективности вычислений.

Некоторые соображения и потенциальные последствия включают в себя:

1. Ограничения выборки: Наблюдаемые несоответствия можно частично объяснить использованием меньшей выборки для повышения эффективности вычислений. Более широкий подход к выборке мог бы обеспечить более полное представление о взаимодействии.

2. Нелинейность или взаимодействия: Отсутствие четко определенных границ и наличие смешанных областей предполагают потенциальную нелинейность или взаимодействие между индикаторами ROC и ATR. Дальнейшие исследования, возможно, с использованием более крупных образцов, могут выявить более тонкие закономерности.

3. Надежность модели: Понимание изменчивости взаимодействия помогает оценить надежность модели и ее чувствительность к различным комбинациям входных функций.

В заключение, интерпретация двухмерного графика частичной зависимости дает ценную информацию о реакции модели на изменения показателей ROC и ATR. Признание потенциального влияния размера выборки на наблюдаемые закономерности, дальнейшее исследование и, если возможно, более обширная стратегия выборки могут повысить точность этих результатов.

Значения аддитивных объяснений Шепли (SHAP)

#pip install shap if you don't have it installed
#Import SHAP
import shap

#Initialise the shap package
shap.initjs()

Несколько факторов, которые следует учитывать:

• Значения SHAP предполагают, что объекты независимы/некоррелированы

• Значения SHAP требуют больших вычислительных затрат для точного расчета. Проблема усугубляется увеличением размерности набора данных.

• Значения SHAP не зависят от модели, то есть они могут не помочь нам уловить определенное поведение, специфичное для модели. В этом заключается как сильная, так и слабая стороны значений.

• Значения SHAP чувствительны к порядку ввода!

В нашем наборе данных есть строгие условия корреляции, и это серьезная проблема при расчете значений SHAP, нарушающая предположение о независимости объектов. К счастью, есть много способов решить эту проблему, например:

• Отказ от коррелирующих функций — это самое простое решение, но в большинстве случаев его следует рассматривать в последнюю очередь

• Использования методов сокращения функций, таких как анализ главных компонентов или других методов выбора функций, с которыми вы можете быть знакомы

• Дискретизация объектов по бинам может помочь смягчить неблагоприятные последствия корреляции в расчетах значений SHAP

• Использование алгоритмов SHAP, предназначенных для обработки коррелированных данных

• Использование некоррелированных функций, например, в нашем случае, Volume и High Low Spread имеют очень слабую корреляцию

В этом случае мы воспользуемся четвертым решением, используя специальные алгоритмы SHAP, предназначенные для обработки коррелированных данных. Алгоритмы SHAP на основе древовидной структуры хорошо справляются с корреляцией.

#Initialise shap value calculator
tree_explainer = shap.TreeExplainer(cat_full)

#Store SHAP values
shap_values = tree_explainer.shap_values(test_x)

#Plot SHAP values
shap.summary_plot(shap_values,test_x)

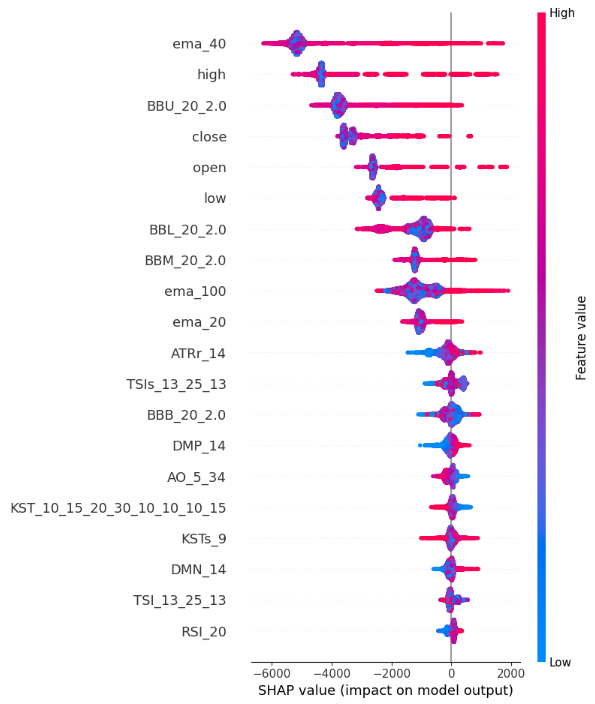
Рис. 13. Графики значений SHAP

Вот как мы интерпретируем сводный график SHAP:

1. Важность функций: функции, перечисленные в верхней части оси Y, оказывают более сильное влияние на увеличение цены закрытия, а функции, расположенные в нижней части оси Y, оказывают более сильное влияние на снижение цены закрытия. 

2. Направление воздействия: каждый объект имеет цветные точки вдоль оси X. Синие точки символизируют более низкие значения функции, а красные - более высокие значения функции. Горизонтальное расположение этих точек говорит нам о влиянии значения функции на цену закрытия. Таким образом, наши расчеты стоимости SHAP показывают, что наш High_Low_Sread не очень указывает на цену закрытия.

3. Величина местоположения: горизонтальное расположение каждой точки вдоль оси X представляет собой величину воздействия, поэтому экстремально высокие и низкие значения оказывают относительно более сильное влияние на цену закрытия по сравнению с функциями Volume, Open и High_Low_Spread в этом демонстрационном примере.

Взаимная информация

from sklearn.feature_selection import mutual_info_regression

mi_scores = mutual_info_regression(train_x, train_y)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=train_x.columns)
mi_scores = mi_scores.sort_values(ascending=False)
mi_scores

ema_100                                       1.965130

ema_40                                         1.960548

ema_20                                         1.933651

BBM_20_2.0                                   1.902066

BBL_20_2.0                                   1.895867

BBU_20_2.0                                  1.881435

high                                             1.795941

low                                              1.786879

close                                            1.783567

open                                            1.777118

TSIs_13_25_13                              0.232247

ATRr_14                                        0.215980

MACDs_12_26_9                            0.214559

KST_10_15_20_30_10_10_10_15    0.208868

KSTs_9                                         0.205177

MACD_12_26_9                            0.174518

TSI_13_25_13                              0.168086

AO_5_34                                     0.128653

BBB_20_2.0                                 0.104481

RSI_20                                         0.095368

MACDh_12_26_9                          0.076360

DMP_14                                      0.060191

DMN_14                                     0.048856

ROC_10                                     0.042115

BBP_20_2.0                               0.028558

CCI_14_0.015                            0.022320

SLOPE_1                                   0.004144

def plot_mi_scores(scores):
    scores = scores.sort_values(ascending=True)
    width = np.arange(len(scores))
    ticks = list(scores.index)
    plt.barh(width, scores)
    plt.yticks(width, ticks)
    plt.title("Mutual Information Scores")

plt.figure(dpi=100, figsize=(8, 5))
plt.grid()
plot_mi_scores(mi_scores)

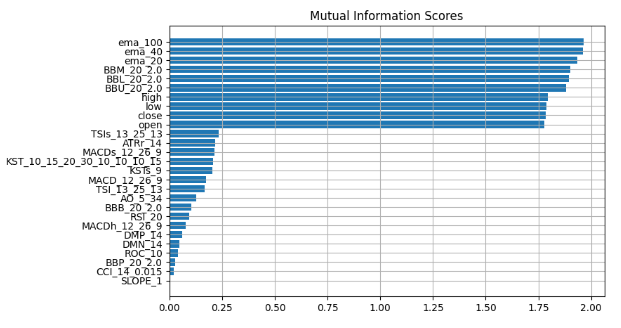
Рис. 14. Значения взаимной информации

Мы наблюдаем постоянный консенсус во всех наших методах объяснения "черного ящика", предполагая, что функции, постоянно выделяемые в этих объяснениях, содержат существенную информацию, которую мы можем эффективно использовать. Экспоненциальная скользящая средняя, полосы Боллинджера и цены открытия максимума, минимума и закрытия последовательно располагаются ближе к вершине, поэтому, измеряя центральную тенденцию, мы можем логически прийти к выводу, что эти функции могут быть очень информативными и поэтому мы можем отказаться от всего остального. 

Давайте проверим наши выводы.

Мы будем использовать две модели: простую линейную регрессию и наш мощный черный ящик. Мы будем выбирать функции, используя информацию, которую мы получили благодаря нашим методам объяснения "черного ящика". 

Сначала мы импортируем необходимые нам зависимости.

from sklearn.linear_model import LinearRegression
from catboost import CatBoostRegressor
from sklearn.metrics import mean_squared_error

Сначала установим более простую модель

#First we fit the simpler model
lm = LinearRegression()

lm.fit(train_x.loc[:,["open","high","low","close"]],train_y)

Затем мы оценим, насколько хорошо более простая модель соответствует обучающим данным.

lm_predictions = pd.DataFrame(lm.predict(train_x.loc[:,["open","high","low","close"]]), index = train_y.index)
lm_fit = lm.predict(train_x.loc[:,["open","high","low","close"]])
residuals = pd.DataFrame(train_y - lm_fit)

Теперь мы воспользуемся нашей более мощной моделью черного ящика, чтобы изучить остатки нашей более простой модели. Мы предоставим нашей модели черного ящика функции, которые, по нашему мнению, являются наиболее информативными.

#Now we bring in our more powerfull black-box model
cat = CatBoostRegressor()
cat.fit(
    train_x.loc[:,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]],
    residuals)

Мы проведем сравнение уровней ошибок на тестовых данных, оценивая производительность нашей первоначальной модели черного ящика, в которой использовались все доступные функции, по сравнению с точностью уточненной модели. Усовершенствованная модель включает в себя более простую линейную регрессию и стратегически использует подмножество тщательно отобранных функций.

lm_test_predictions = pd.DataFrame(lm.predict(test_x.loc[:,["open","high","low","close"]]),index=test_y.index)
cat_full_test_predictions = cat_full.predict(test_x[predictors])

cat_residuals_predictions = pd.DataFrame(cat.predict(test_x.loc[:,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]]),index=test_y.index)

Оценим уровень ошибок нашего исходного черного ящика.

full_error = mean_squared_error(test_y,cat_full_test_predictions)

И сравним его с уровнем ошибок нашего нового гибрида черного ящика.

hybrid_predictions = lm_test_predictions.iloc[:,0] + cat_residuals_predictions.iloc[:,0]
hybrid_error = mean_squared_error(test_y, hybrid_predictions)

delta_error = full_error - hybrid_error
(delta_error / full_error) * 100

94.428

Наш новый гибрид "черного ящика" имеет показатели ошибок, которые улучшились на 94%.

hybrid_predictions.plot()

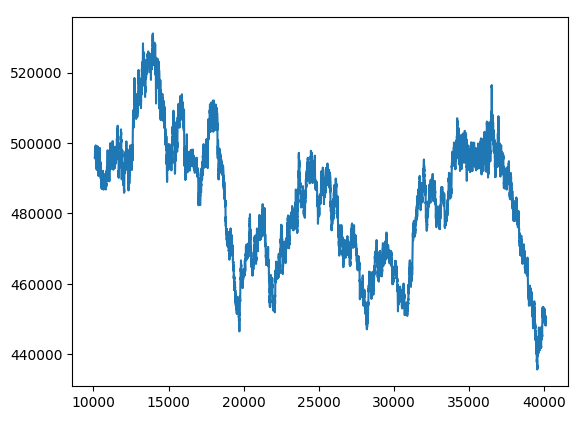
Рис. 15. Новый прогноз "черного ящика"

Первостепенное значение имеет заметное повышение реалистичности наших новых прогнозов "черного ящика", лишенных неестественных флетовых периодов, наблюдавшихся первоначально. Теперь мы достигаем повышенной точности с помощью оптимизированного набора функций. Это подчеркивает принцип, согласно которому при эффективном выполнении мы можем добиться большего с меньшими усилиями.

Соберем все вместе

Мы готовы интегрировать все компоненты в комплексную торговую стратегию.

MARKET_SYMBOL = "Volatility 75 Index"
DEVIATION = 100
VOLUME = 0
symbol_info = MT5.symbol_info(MARKET_SYMBOL)
VOLUME = symbol_info.volume_min * 1

def preprocess(df):
    #20 period exponential moving average
    df["ema_20"] = df.ta.ema(length=20)
    #40 period exponential moving average
    df["ema_40"] = df.ta.ema(length=40)
    #100 period exponential moving average
    df["ema_100"] = df.ta.ema(length=100)
    #20 period bollinger bands with 3 standard deviations
    df.ta.bbands(length=20,sd=2,append=True)
    df = df.loc[100:,:]

def fetch_prices():
    current_prices = pd.DataFrame()
    current_prices = pd.DataFrame(MT5.copy_rates_from_pos(MARKET_SYMBOL,MT5.TIMEFRAME_M1,0,200))
    preprocess(current_prices)
    return(current_prices)

def normalise_prices(raw_data):
    for col in raw_data.columns:
        if col in first_values:
            raw_data[col] = raw_data[col] / first_values[col]

model_forecast = 0

def hybrid_forecast(model_1,model_2):
    market_data = fetch_prices()
    normalise_prices(market_data)
    forecast_1 = model_1.predict(market_data.loc[199:200,["open","high","low","close"]])
    forecast_2 = model_2.predict(market_data.loc[199:200,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]])
    out = forecast_1 + forecast_2
    return(out)

INITIAL_BALANCE = MT5.account_info().balance
CURRENT_BALANCE = 0

if __name__ == "__main__":
    while True:
        
        #Account standing
        info = MT5.account_info()
        CURRENT_BALANCE = info.balance
        profit = CURRENT_BALANCE - INITIAL_BALANCE
        
        model_forecast = hybrid_forecast(lm,cat)
        print("Current forecast: ",model_forecast)
        
        #We have no open positions
        if(MT5.positions_total() == 0):
            print("No open positions")
            
            #Buy
            if(model_forecast > MT5.symbol_info(MARKET_SYMBOL).ask):
                print("Following model forecast buy")
                MT5.Buy(MARKET_SYMBOL,VOLUME)
                last_trade = 1
                        
            #Sell    
            elif(model_forecast < MT5.symbol_info(MARKET_SYMBOL).ask):
                print("Following model forecast sell")
                MT5.Sell(MARKET_SYMBOL,VOLUME)
                last_trade = 0
                
        elif(MT5.positions_total() > 0):
            print("Checking model forecast")
            
            if((model_forecast > MT5.symbol_info(MARKET_SYMBOL).ask) & (last_trade == 0)):
                print("Model is forecasting a move that hurts our exposure. Closing positions")
                MT5.Close()
            
            elif((model_forecast < MT5.symbol_info(MARKET_SYMBOL).ask) & (last_trade == 1)):
                print("Model is forecasting a move that hurts our exposure. Closing positions")
                MT5.Close()
                
        print("Total Profit/Loss: ",profit)
        time.sleep(60)

Current forecast: [239100.04622681] No open positions Following model forecast buy Total Profit/Loss: 0.0

Заключение

По мере того, как мы продвигаемся к обучению более крупных и сложных моделей, их становится все сложнее понимать, объяснять и отлаживать. Не имея возможности полностью понять, как именно устроены наши модели машинного обучения и почему они принимают те или иные решения, мы не можем быть уверены, что модель работает так, как мы предполагаем. Неспособность понять модели и устранить неполадки не гарантирует дополнительных сложностей, возникающих при использовании этих методов. Ценность, которую мы можем стабильно извлечь из инструмента, ограничена тем, насколько мы понимаем этот инструмент. Именно с этой целью и была написана эта статья - чтобы побудить вас больше доверять своим моделям и получить более глубокое представление о вращающихся винтиках моделей машинного обучения, находящихся в "черном ящике".