MetaTrader 5 / Машинное обучение
Español Português
preview
Нейронная сеть на практике: Первый нейрон

Нейронная сеть на практике: Первый нейрон

MetaTrader 5 — Машинное обучение | 17 октября 2024, 09:28
685 0
Daniel Jose
Daniel Jose

Введение

Всем привет и добро пожаловать в новую статью о нейронных сетях. В предыдущей статье Нейронная сеть на практике: Зарисовка нейрона, мы создаем базовую, начальную схему для построения простого нейрона. Однако тот простой нейрон, который мы создаем, - это не совсем то, что нам нужно. Это связано с тем, что у него есть небольшой недостаток. Но я хочу, чтобы вы поняли, как строится нейронная сеть шаг за шагом. Данный недостаток не сильно влияет на работу этого простого нейрона.

Возможно, вы думаете: "Что это за недостаток, о котором он говорит? Я не заметил ничего плохого. Нейрон прекрасно работал в моих тестах". Вернемся немного назад в этой серии статей о нейронных сетях, чтобы понять, о чем я говорю.

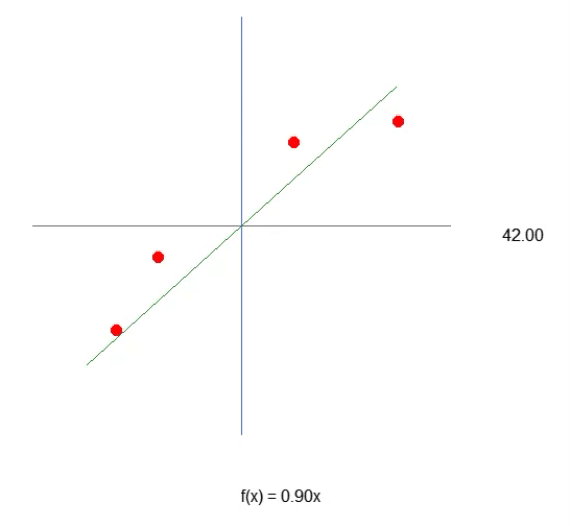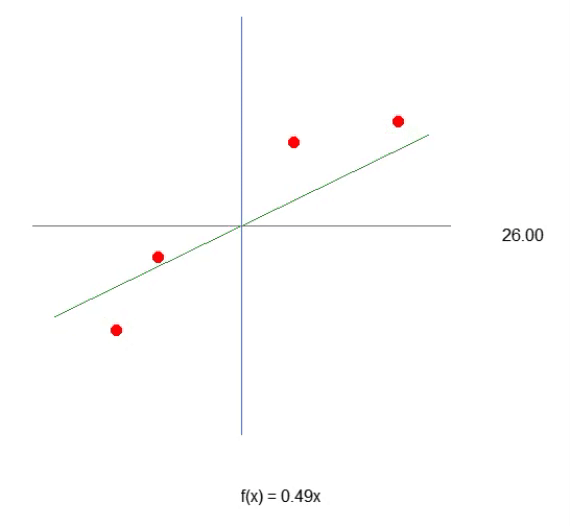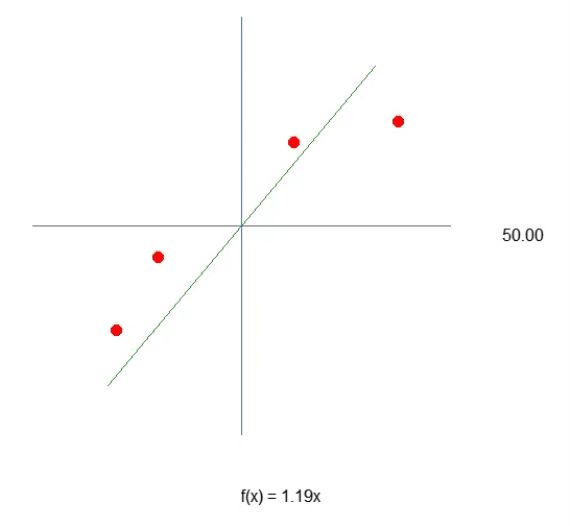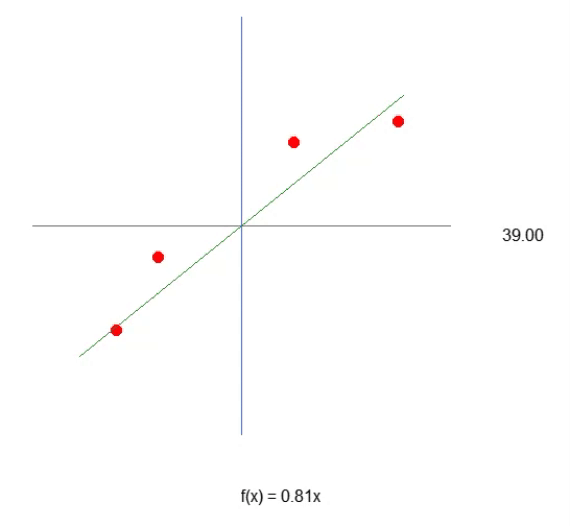
В первых статьях о нейронных сетях мы рассмотрели, как можно заставить машину создавать уравнение прямой линии. Изначально уравнение ограничивалось началом координат на декартовых осях, то есть прямая должна была проходить через точку (0, 0). Это объясняется тем, что значение константы < b > в приведенном ниже уравнении равно нулю.

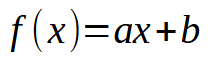
Хотя мы использовали метод наименьших квадратов для поиска подходящего уравнения, чтобы набор данных или предварительные знания, содержащиеся в базе данных, можно было адекватно представить в виде математического уравнения, такое моделирование не помогло найти действительно подходящее уравнение. Это связано с тем, что в зависимости от данных, находящихся в базе знаний, нам потребуется, чтобы значение константы < b > было ненулевым.

Если спокойно изучить предыдущие статьи, то можно заметить, что для определения наилучшего возможного значения как константы < a >, которая является угловым коэффициентом, так и константы < b >, которая является точкой пересечения, потребовалось некоторое математическое жонглирование. Данные манипуляции позволили найти наиболее подходящее уравнение прямой линии, причем было показано два способа сделать это: один - с помощью вычисления производных, другой - с помощью матричных вычислений.

Однако теперь, для всего того, что нам нужно сделать, такие вычисления не пригодятся, поскольку нам нужно смоделировать другой способ поиска констант уравнения прямой. В предыдущей статье мы показали, как можно найти константу, представляющую собой угловой коэффициент. Надеюсь, вам было интересно и вы много экспериментировали с этим кодом, потому что сейчас мы сделаем кое-что более сложное. Однако, несмотря на сложности, на самом деле это открывает двери для многих других вещей. Это, пожалуй, самая интересная статья, которую вы прочтете в этой серии о нейронных сетях, потому что после нее всё станет намного проще и практичнее.


Почему они так любят всё усложнять

Итак, прежде чем мы перейдем к собственно коду, я хотел бы помочь вам понять несколько моментов. Обычно, когда мы ищем нейронные сети, мы сталкиваемся с множеством терминов, буквально целым вагоном понятий. Я не знаю, почему те, кто объясняет, что такое нейронные сети, так стремятся усложнить то, что и так просто. На мой взгляд, для этого нет никаких причин, но я здесь не для того, чтобы осуждать или преуменьшать. Я здесь, чтобы объяснить, как всё работает за кулисами.

Для простоты я остановлюсь на нескольких терминах, которые часто встречаются при разговоре о нейронных сетях. Вот первый: Вес. Этот термин обозначает именно угловой коэффициент уравнения прямой линии. Как бы вы его ни называли, термин "вес" просто обозначает угловой коэффициент. Еще один широко разрекламированный термин: Смещение. Об этом термине, также можно услышать такое: смещение - не такая уж большая проблема, и она не ограничивается только нейронными сетями или искусственным интеллектом. Но ничего подобного. Данный термин - не что иное, как точка пересечения. Помните, что мы имеем дело с секущей линией. Пожалуйста, не путайте понятия.

Из этих, казалось бы, посторонних терминов возникает множество других понятий и выражений, но все они, абсолютно все, не новы. На самом деле, это просто разные названия одних и тех же вещей. Я не буду вдаваться в то, почему знакомым понятиям даются разные названия. Однако если при изучении нейронных сетей или чего-либо еще, связанного с ними, вы увидите, что появляются странные термины, постарайтесь понять, что за математическая формула стоит за всем этим, и вы увидите, что в действительности всё гораздо проще, чем кажется на первый взгляд.

Я говорю так, потому что есть много людей, которые любят всё усложнять.

Они берут что-то простое и начинают придумывать ряд дополнительных элементов, просто чтобы усложнить то, что может понять каждый. Когда речь идет о программировании или точных науках, то чем проще, тем лучше. Когда всё начинает обрастать украшениями или элементами, отвлекающими наше внимание, пора остановиться, убрать всю эту косметику, и посмотреть на истинную реальность. Многие скажут, что это сложно, ведь нужно быть экспертом в этой области, чтобы понять или реализовать нейронную сеть, что это можно сделать только с помощью того или иного языка, или с помощью того или иного ресурса. Но к этому моменту вы уже должны были заметить, что нейронная сеть - это совсем не сложно. Всё очень просто.

Итак, теперь перейдем к новой теме. Мы рассмотрим, как можно добавить значение константы < b >, которая является точкой пересечения, или, как некоторые предпочитают ее называть: смещение или предвзятость. Это необходимо для того, чтобы уравнение линии более точно отражало базу данных, которую мы используем для обучения нейрона.


Появление первого нейрона

Чтобы наш первый нейрон ожил, и как только он оживет, нам больше не понадобится его модифицировать, как можно будет увидеть ниже. Сначала нужно понять, с чем мы имеем дело. Наш текущий нейрон ведет себя так, как можно видеть на анимации ниже.



Эту же анимацию можно увидеть в статье "Нейронная сеть на практике: Секущая линия". Другими словами, мы только что осуществили первый шаг к созданию нейрона, который может делать то, что раньше мы делали вручную с помощью клавиш со стрелками. Однако вы наверное заметили, что этого недостаточно. На самом деле, нам нужно включить константу пересечения, чтобы еще улучшить наше уравнение. Возможно, вы думаете, что сделать это будет очень сложно, но на самом деле, это настолько просто, что даже скучно. Обратите внимание на то, как мы добавляем константу пересечения к нейрону. Это можно увидеть во фрагменте ниже. 

01. //+------------------------------------------------------------------+
02. double Cost(const double w, const double b)
03. {
04.     double err, fx, x;
05. 
06.     err = 0;
07.     for (uint c = 0; c < nTrain; c++)
08.     {
09.         x = Train[c][0];
10.         fx =  a * w + b;
11.         err += MathPow(fx - Train[c][1], 2);
12.     }
13. 
14.     return err / nTrain;
15. }
16. //+------------------------------------------------------------------+

Я стараюсь разбивать код на фрагменты, чтобы вы могли детально понять то, что делается. А потом скажите мне: сложно это или нет? Действительно ли нужны все эти сложности?

Будьте внимательны, потому что уровень сложности почти смешной. (СМЕХ). В девятой строке мы берем наше обучающее значение и помещаем его в переменную X. Затем, в десятой строке, мы выполняем факторизацию. Надо же! Какой сложный счет! Но подождите, разве это не то самое уравнение, которое было показано в начале? Знаменитое уравнение прямой линии. Вы шутите! Это не будет работать как нейрон, используемый в программах искусственного интеллекта.

Не беспокойтесь, мои дорогие читатели. Вы увидите, что это работает, как и любая другая программа искусственного интеллекта или нейронной сети, неважно, насколько сложной они хотят ее сделать. Вы увидите, что это точно так же, как и в любой нейронной сети. Что изменится - это следующий шаг, который можно увидеть в ближайшее время. Но изменения не так велики, как вы себе представляете. Не волнуйтесь, мы будем идти шаг за шагом.

После обновления вычисления ошибки, мы можем обновить фрагмент, который будет регулировать эти два параметра в функции стоимости. Это будет происходить постепенно, чтобы вы могли понять некоторые детали. Первое, что мы сделаем, - изменим оригинальный код, представленный в предыдущей статье, на новый код, показанный ниже. 

01. //+------------------------------------------------------------------+
02. void OnStart()
03. {
04.     double weight, ew, eb, e1, bias;
05.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
06. 
07.     Print("The first neuron...");
08.     MathSrand(512);
09.     weight = (double)macroRandom;
10.     bias = (double)macroRandom;
11. 
12.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
13.     {
14.         ew = (Cost(weight + eps, bias) - e1) / eps;
15.         eb = (Cost(weight, bias + eps) - e1) / eps;
16.         weight -= (ew * eps);
17.         bias -= (eb * eps);
18.         if (f != INVALID_HANDLE)
19.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
20.     }
21.     if (f != INVALID_HANDLE)
22.         FileClose(f);
23.     Print("Weight: ", weight, "  Bias: ", bias);
24.     Print("Error Weight: ", ew);
25.     Print("Error Bias: ", eb);
26.     Print("Error: ", e1);
27. }
28. //+------------------------------------------------------------------+

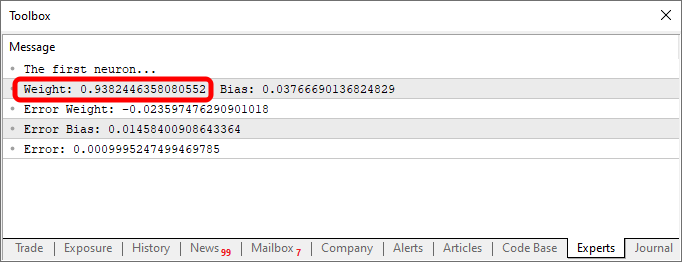
Когда мы запустим скрипт после этих изменений, мы увидим нечто похожее на изображение ниже.


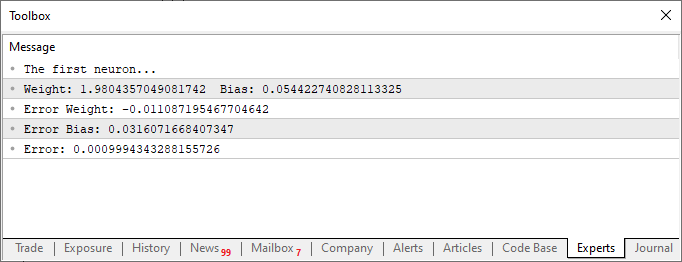
Теперь давайте рассмотрим только второй фрагмент кода. В четвертой строке мы добавляем и изменяем некоторые переменные, что-то очень простое. В десятой строке мы указываем приложению определить случайное значение для смещения, или нашей константы пересечения. Теперь обратите внимание, что нам нужно также передать данное значение в функцию Cost. Это делается в строках 12, 14 и 15. Однако самое интересное заключается в том, что мы будем генерировать два вида накапливающихся ошибок: одну для значения веса и одну для значения смещения. Надо понять, что, хотя оба эти параметра являются частью одного уравнения, их нужно настраивать по-разному. Поэтому мы должны знать, какую ошибку представляет собой каждая из них в общей системе.

Зная это, в строках 16 и 17 мы сможем правильно задать значения для следующей итерации цикла for. Теперь (как и в предыдущей статье) мы также сбрасываем значения в CSV-файл. Это позволит нам построить график, чтобы изучить, как корректируются эти значения.

На данный момент наш первый нейрон полностью создан, но есть еще некоторые детали, которые вы сможете понять, если посмотрите на полный код этого нейрона. Полный код приведен ниже. 

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w, const double b)
18. {
19.     double err, fx, a;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.     {
24.         a = Train[c][0];
25.         fx =  a * w + b;
26.         err += MathPow(fx - Train[c][1], 2);
27.     }
28. 
29.     return err / nTrain;
30. }
31. //+------------------------------------------------------------------+
32. void OnStart()
33. {
34.     double weight, ew, eb, e1, bias;
35.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
36. 
37.     Print("The first neuron...");
38.     MathSrand(512);
39.     weight = (double)macroRandom;
40.     bias = (double)macroRandom;
41. 
42.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
43.     {
44.         ew = (Cost(weight + eps, bias) - e1) / eps;
45.         eb = (Cost(weight, bias + eps) - e1) / eps;
46.         weight -= (ew * eps);
47.         bias -= (eb * eps);
48.         if (f != INVALID_HANDLE)
49.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
50.     }
51.     if (f != INVALID_HANDLE)
52.         FileClose(f);
53.     Print("Weight: ", weight, "  Bias: ", bias);
54.     Print("Error Weight: ", ew);
55.     Print("Error Bias: ", eb);
56.     Print("Error: ", e1);
57. }
58. //+------------------------------------------------------------------+

Наверняка вы заметили кое-что интересное как в коде, так и в результате, показанном на изображении выше. В шестой строке находятся значения, используемые для обучения нейрона. Очевидно, что при умножении используется значение два. Однако нейрон сообщает нам, что это значение: 1.9804357049081742. Также видно, что точка пересечения должна быть равна нулю, но нейрон говорит нам, что это так: 0.054422740828113325. Хорошо, учитывая, что в строке 15 мы допускаем, что ошибка может быть от: 0,001, не так плохо. Это связано с тем, что конечная ошибка, о которой сообщил нейрон, была: 0,0009994343288155726, то есть ниже предела погрешности, который мы считаем приемлемым.

Данные различия, которые вы можете отчетливо заметить, являются показателем вероятности того, что информация верна. Обычно это выражается в процентах. Однако мы никогда не увидим 100 %. Число может приближаться к 100%, но оно никогда не будет точным из-за этого небольшого отклонения от правильного результата.

Однако данный показатель вероятности не является индексом уверенности в той или иной информации. Мы пока не работаем над созданием этого второго индекса. Пока что мы просто проверяем, способен ли нейрон установить корреляцию между обучающими данными. Но, возможно, вы уже думаете: "Этот нейрон бесполезен, потому что в том виде, в котором вы его создали, он не годится ни для чего другого. Он служит только для поиска числа, которое мы и так уже знаем. На самом деле мне нужна система, которая могла бы рассказывать мне о чем-то, написать текст или код, даже программу, которая сможет торговать на финансовом рынке и дать какую-то прибыль.

Вы, безусловно, преследуете большие интересы, но если вы только смотрите на нейронные сети или на искусственный интеллект с намерением заработать деньги, боюсь, у вас ничего не получится. Единственные люди, которые действительно заработают на этом, - это те, кто продает нейросети или системы искусственного интеллекта. Это происходит, когда им удается убедить других в том, что искусственный интеллект или нейронные сети могут работать лучше, чем хороший профессионал. Кроме этих людей, которые собираются забрать все деньги у других путем продажи таких продуктов, никто больше на этом не заработает. Если бы это действительно было так, то зачем мне писать эти статьи с объяснениями? Или почему некоторые люди, не менее осведомленные в том, как работают данные механизмы, должны объяснять, как они работают? Это бессмысленно. Они могут просто молчать и зарабатывать деньги. Но на практике всё происходит иначе. По этой причине, вам лучше забыть о том, что вы создадите нейронную сеть и, не имея никаких знаний, заработайте деньги, просто собирая коде то тут, то там.

Однако ничто не мешает вам создать небольшую нейронную сеть, цель которой - помочь вам принимать решения, покупать, продавать или даже визуализировать некоторые аспекты рынка. Возможно ли это сделать? Да, конечно. На самом деле, изучив всё нужное, вы медленно и с большими усилиями и самоотдачей, но сможете обучить нейронную сеть этому. Но, как я только что сказал, вам придется потрудиться. Однако это вполне возможно.

У нас есть первый нейрон. Но прежде чем прийти в восторг, давайте лучше посмотрим, как он устроен. Для наглядности посмотрите на рисунок ниже.

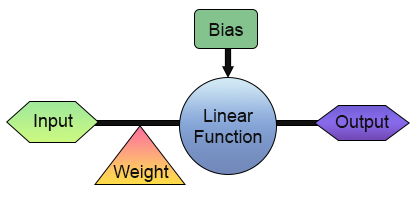
На этом изображении видно, что реализовано в нашем нейроне. Обратите внимание: у него есть вход и выход. Этот единственный вход получает вес. Возможно, это не так уж и полезно, ведь какой смысл в присутствии входа и выхода? Хорошо, я понимаю ваше скептическое отношение к этому, но вы можете не знать (это зависит от того, насколько хорошо вы разбираетесь в различных темах), что в цифровой электронике есть схема, которая имеет вход и выход. На самом деле их два. Один из них - инвертор, а другой - буфер. Оба являются неотъемлемыми частями еще более сложных компонентов, и этот нейрон может узнать, как работают обе схемы. Для этого нужно просто его обучать, и для обучения, достаточно изменить матрицу обучения на одну из тех, что показаны ниже. 

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 1},
                    {1, 0},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

Используя данный фрагмент кода, вы получите нечто подобное тому, что показано на рисунке ниже:


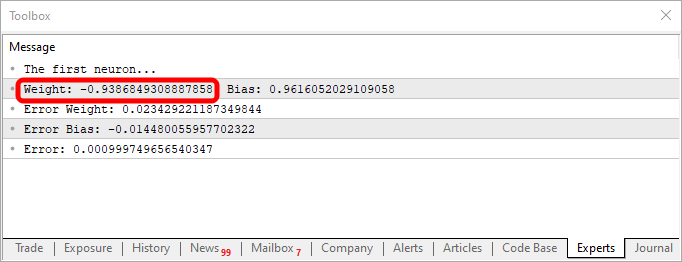
Обратите внимание, что значение веса отрицательно, и это означает, что мы будем инвестировать в входящее значение. Другими словами, у нас есть инвертор. Используя приведенный ниже фрагмент, мы получим другой выход.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 0},
                    {1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

Выходные данные в этом случае можно увидеть на рисунке ниже.


Обратите внимание, что значение веса теперь положительное. И это означает, что мы храним входы непосредственно на выходах. То есть, у нас есть буфер. Посмотрите, как интересно экспериментировать с ним.

Простое изменение информации в базе знаний или базе данных, которая в нашем случае представляет собой двумерный массив, уже позволяет самому коду создавать уравнения для представления вещей. И по этой причине абсолютно все, кто интересуется программированием, с удовольствием работают с нейронными сетями. С ними очень интересно работать.

Однако этот первый нейрон весьма ограничен, но не из-за своей конструкции, а потому что он позволяет нам получить только один вход. На практике нейроны нейронной сети могут иметь столько входов, сколько необходимо. Аналогично, они могут иметь столько выходов, сколько необходимо для выполнения их задач. Я излагаю всё постепенно, чтобы не перегрузить вас. Я хочу, чтобы вы поняли, как работает этот механизм. Конечно, как бы ни старались, мы никогда не сможем показать всё, что можно сделать с помощью этого механизма. Ведь возможности зависят только от нашей креативности. Но сейчас мы сделаем его немного интереснее и, в то же время, увлекательнее.


Сигмоидная функция

С этого момента всё, что я вам покажу, будет лишь верхушкой айсберга. Каким бы крутым, веселым, сложным или захватывающим ни казалось программирование, Отныне абсолютно всё будет лишь малой толикой того, что мы можем сделать. Так что с этого момента вы должны становиться более самостоятельными. Я просто хочу направить вас на правильный путь. Не стесняйтесь экспериментировать с предложенным материалом. Ведь, как уже говорилось, единственным ограничивающим фактором будет ваше воображение.

Для того, чтобы наш одиночный нейрон мог обучаться при наличии большего количества доступных входов, вам нужно понять одну маленькую и простую деталь. Это можно увидеть ниже.

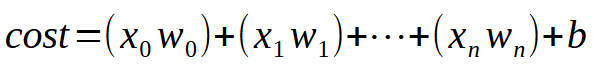
Если говорить вкраце, то ниже приведено то же самое уравнение.

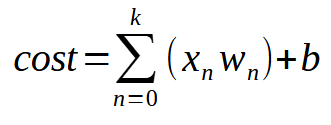
Значение < k > - это количество входов, которые могут быть у нашего нейрона. Таким образом, независимо от количества входов, нам нужно лишь добавить столько входов, сколько необходимо для того, чтобы нейрон научился справляться с каждой новой ситуацией. Однако, начиная со второго входа, функция уже не является уравнением прямой линии, а уравнением любой возможной формы. Это необходимо для того, чтобы нейрон мог найти наилучший способ обработки различных видов обучения.

Теперь всё становится по-настоящему серьезным, поскольку мы можем заставить один нейрон обучаться нескольким разным вещам. Однако есть небольшая проблема, связанная с тем, что уравнение прямой линии больше не обрабатывается. Чтобы понять это, давайте изменим программу так, чтобы она выглядела следующим образом: 

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow(((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < 3000) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

При выполнении данного кода вы получите результат, аналогичный изображенному ниже:


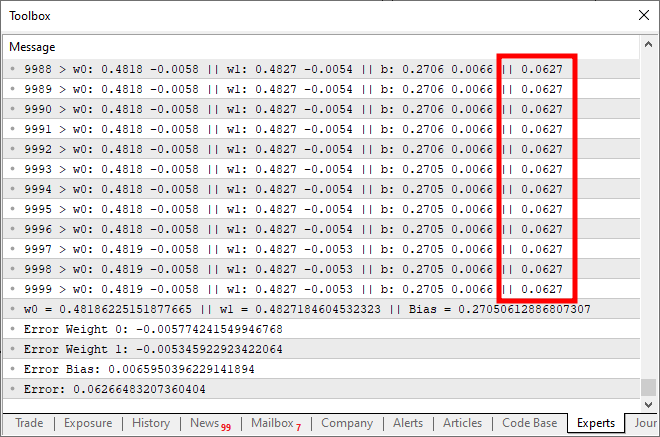
Что же здесь не так? Если вы заметили, мы просто добавили в код возможность новых записей, и это сделано хорошо. Но обратите внимание: примерно на десяти тысячах итераций стоимость просто перестает уменьшаться, а если и уменьшается, то очень медленно. Почему? Причина в том, что в нейроне чего-то не хватает. Это не было необходимым при работе с одним входом, но становится крайне важным, когда мы хотим добавить новые. Он также используется при работе со слоями нейронов, что характерно для глубокого обучения, но об этом мы поговорим позже. Пока что давайте сосредоточимся на главном. Нейрон достигает точки стагнации, когда он больше не может снижать расходы. Данная проблема решается добавлением триггерной функции прямо на выходе. Функции и порядок действий здесь во многом зависят от вида задачи, которую мы хотим выполнить. Единого способа решения этой части не существует, ведь можно использовать различные функции активации. Однако обычно используется сигмоид, и причина проста. Данная функция позволяет принимать значения от плюс бесконечности до минус бесконечности в диапазоне от 0 до 1. В некоторых случаях мы изменяем его таким образом, чтобы этот диапазон находился между 1 и -1, но здесь мы используем базовую версию. Сигмоидная функция представлена следующей формулой:

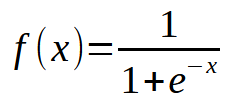
Но как применить это в нашем коде? Это может показаться очень сложным, но на самом деле, всё гораздо проще, чем кажется. В том же самом коде, показанном выше, нужно будет изменить совсем немногое:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

И когда мы запустим код, показанный выше, результат будет похож на это:


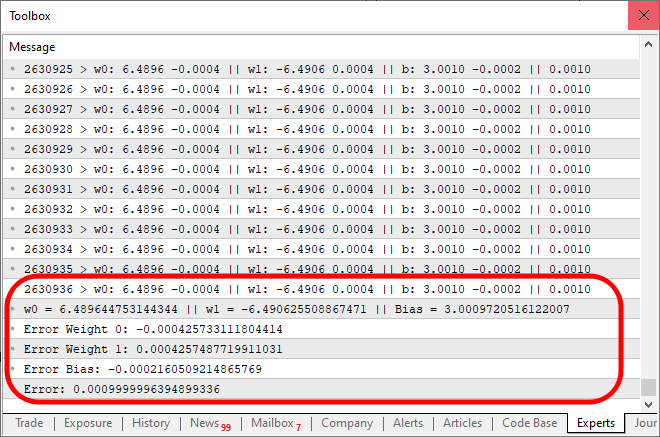
Интересно, что для достижения ожидаемого результата в пределах погрешности потребовалось 2 630 936 итераций, что совсем не плохо. У вас может сложиться впечатление, что программа начинает работать немного медленно, так как мы используем только центральный процессор. Но это впечатление связано с тем, что мы печатаем сообщение на каждой итерации кода. Мы можем сделать код немного быстрее, если изменим данный способ отображения на новый метод. В то же время мы добавим небольшой код для проверки возможностей нейрона. Итоговый код выглядит так:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;
    ulong count;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (count = 0; (count < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); count++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
    }
    PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", count, w0, ew0, w1, ew1, bias, eb, err);
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);

    Print("Testing the neuron...");
    for (uchar p0 = 0; p0 < 2; p0++)
        for (uchar p1 = 0; p1 < 2; p1++)
            PrintFormat("%d OR %d IS %f", p0, p1, macroSigmoid((p0 * w0) + (p1 * w1) + bias));
}
//+------------------------------------------------------------------+

При запуске данного кода в терминале может появиться следующее:


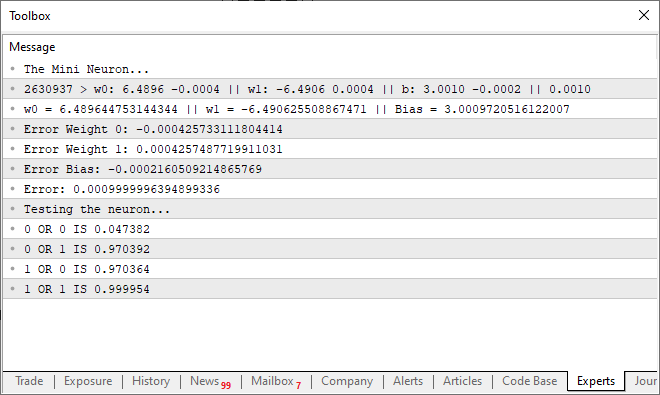
То есть мы заставили наш простой нейрон понять, как работает логический вентиль. Теперь мы вступаем на путь невозврата, поскольку наш одиночный нейрон уже начинает учиться более сложным вещам, чем простое понимание того, связано ли что-то друг с другом или нет.


Заключительные идеи

В сегодняшней статье мы начали создавать нечто, в некотором смысле, удивительное. Ведь этот простой и скромный нейрон, который мы смогли запрограммировать с помощью очень небольшого количества кода на MQL5, продемонстрировал свои возможности. Многие говорят, что для данной задачи требуется тысяча и один ресурс, но я надеюсь, что вы поняли, как развивается этот процесс. В всего лишь нескольких статьях я подвел итог длительной работы, проделанной несколькими исследователями. Несмотря на относительную простоту, разработка того, как должны реализовываться вещи, потребовала времени. Настолько, что даже сегодня ведутся исследования, направленные на то, чтобы сделать все эти вычисления более плавными и быстрыми. Здесь мы используем только один нейрон с двумя входами, пятью параметрами и одним выходом. И всё же обратите внимание, что системе требуется некоторое время, чтобы найти нужное уравнение.

Конечно, мы можем использовать OpenCL, чтобы ускорить работу с GPU, но, на мой взгляд, пока рано думать о таком решении. Мы можем пойти еще дальше, прежде чем возникнет необходимость в реальном использовании GPU для вычислений. Однако если есть желание углубиться в нейронные сети, я настоятельно рекомендую вам рассмотреть возможность приобретения графического процессора, поскольку он значительно ускорит работу некоторых видов нейронных сетей.

В приложении вы можете получить доступ к последней версии кода, представленной в этой статье. Используйте его по своему усмотрению и экспериментируйте свободно. Таким образом вы убедитесь в том, как этот нейрон справляется с различными ситуациями, и найдете его ограничения, ведь они у него есть. В связи с этой причиной нам еще предстоит изучить дополнительные вопросы.

Перевод с португальского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/pt/articles/13745

Прикрепленные файлы |
Загрузить ZIP
Anexo.mq5 (2.22 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Возможности Мастера MQL5, которые вам нужно знать (Часть 21): Тестирование с данными экономического календаря Возможности Мастера MQL5, которые вам нужно знать (Часть 21): Тестирование с данными экономического календаря
Данные экономического календаря по умолчанию недоступны для тестирования с помощью советников в тестере стратегий. Мы рассмотрим, как базы данных могут помочь обойти это ограничение. В частности, мы увидим, как можно использовать базы данных SQLite для архивирования новостей Экономического календаря, чтобы советники, собранные с помощью Мастера, могли использовать их для генерации торговых сигналов.
Нейросети в трейдинге: Анализ рыночной ситуации с использованием Трансформера паттернов Нейросети в трейдинге: Анализ рыночной ситуации с использованием Трансформера паттернов
В анализе рыночной ситуации нашими моделями ключевым элементом является свеча. Тем не менее давно известно, что свечные паттерны могут помочь в прогнозировании будущих ценовых движений. И в этой статье мы познакомимся с методом, который позволяет интегрировать оба этих подхода.
Разработка системы репликации (Часть 49): Все усложняется (I) Разработка системы репликации (Часть 49): Все усложняется (I)
В этой статье мы немного усложним ситуацию. Используя то, что было показано в предыдущих статьях, мы начнем открывать доступ к файлу шаблона, чтобы пользователь мог использовать свой собственный шаблон. Однако я буду вносить изменения постепенно, так как также буду дорабатывать индикатор, чтобы снизить нагрузку на MetaTrader 5.
Построение экономических прогнозов: потенциальные возможности Python Построение экономических прогнозов: потенциальные возможности Python
Как использовать экономические данные Всемирного банка для прогнозирования? Что будет если совместить модели ИИ и экономику?