Нейросети в трейдинге: Двухмерные модели пространства связей (Chimera)

MetaTrader 5 — Торговые системы | 17 февраля 2025, 10:47

195

Dmitriy Gizlyk

Введение

Моделирование временных рядов представляет собой сложную задачу, имеющую широкое применение в различных областях, включая медицину, финансовые рынки и энергетику. Основные трудности при разработке универсальных моделей временных рядов связаны с:

Необходимостью учета многомасштабных зависимостей, среди которых: краткосрочные автокорреляции, сезонность и долгосрочные тенденции. Это требует использования гибких и мощных архитектур.
Адаптивной обработкой многомерных временных рядов, в которых взаимосвязь между анализируемыми переменными может быть динамической и нелинейной. Для этого необходима разработка механизмов, учитывающих контекстно-зависимые взаимодействия.
Минимизацией потребности в ручной предобработке данных, обеспечивая автоматическое выявление структурных закономерностей без необходимости сложной настройки параметров.
Эффективностью вычислений, особенно при работе с длинными последовательностями, что требует оптимизации архитектуры модели с целью эффективного использования вычислительных ресурсов и снижения затрат на обучение.

Классические статистические методы требуют значительной предобработки исходных данных и не всегда адекватно захватывают сложные нелинейные зависимости. Глубокие нейросетевые архитектуры продемонстрировали высокую выразительность, но квадратичная вычислительная сложность моделей на основе архитектуры Transformer делает их трудно применимыми для многомерных временных рядов с большим количеством анализируемых признаков. Кроме того, такие модели часто не различают сезонные и долгосрочные компоненты, либо используют жесткие априорные допущения, что снижает их адаптивность в различных прикладных сценариях.

Один из вариантов решения указанных проблем был предложен в работе "Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models". Фреймворк Chimera — это двухмерная модель пространства состояний (2D-SSM), которая использует линейные преобразования как вдоль временной оси, так и вдоль оси переменных. Фреймворк Chimera включает три основных компоненты — модели пространства состояний вдоль временного измерения, вдоль анализируемых переменных и поперечных переходов между этими измерениями. Параметризация Chimera основана на компактных диагональных матрицах, что делает её способной восстанавливать как классические статистические методы, так и современные SSM-архитектуры.

Дополнительно, Chimera использует адаптивную дискретизацию для учета сезонных паттернов и особенностей динамических систем.

В своей работе авторы Chimera провели анализ производительности предложенного фреймворка на различных задачах многомерных временных рядов (классификации, прогнозирования и обнаружения аномалий). Представленные результаты экспериментов показывают, что Chimera достигает точности, сопоставимой, или превосходящей современные методы, при общем снижении вычислительных затрат.

Алгоритм Chimera

Модели пространства состояний (SSM) занимают важное место в методах анализа временных рядов, благодаря своей простоте, а также выразительным возможностям для моделирования сложных зависимостей, включая авторегрессионные. Эти модели используются для представления систем, где состояние на текущий момент времени зависит от предшествующего состояния анализируемой окружающей среды. Однако, традиционно SSM описывают системы, в которых состояние зависит от одной переменной (например, времени). Это ограничивает их применение в случаях, когда требуется моделирование многомерных временных рядов, поскольку необходимо захватывать зависимости, как во временном контексте, так и в контексте анализируемых переменных.

Многомерные временные ряды представляют собой более сложные структуры, которые требуют наличия методов, способных учитывать взаимозависимости между несколькими переменными одновременно. Классические двухмерные модели пространства состояний (2D-SSM), использующиеся для описания таких структур, испытывают ряд ограничений, что сдерживает их эффективность по сравнению с современными методами глубокого обучения. Здесь можно выделить следующие недостатки:

Ограничение на линейные зависимости. Классические 2D-SSM способны моделировать лишь линейные взаимосвязи, что становится значительным ограничением при попытках описания более сложных, нелинейных зависимостей, характерных для реальных многомерных временных рядов.
Дискретность модели. Эти модели часто имеют заранее заданное разрешение и не могут автоматически подстраиваться под изменение характеристик данных. Это делает их неэффективными для моделирования сезонных или других закономерностей, имеющих переменное разрешение.
Сложности с обработкой больших наборов данных. В практическом применении 2D-SSM часто оказываются неэффективными для работы с большими объемами данных, что ограничивает их использование в реальных задачах.
Статичность параметров обновления. Классические методы обновления параметров модели фиксированы, что не позволяет адекватно учитывать динамику зависимостей, которая может изменяться со временем. Это является значительным ограничением в приложениях, где данные эволюционируют и требуют адаптивных подходов.

С другой стороны, методы глубокого обучения, которые активно развиваются в последние годы, предлагают потенциал для преодоления ряда этих ограничений. С их помощью можно моделировать более сложные, нелинейные зависимости и учитывать динамику временных рядов, что делает их перспективными для применения в задачах анализа многомерных данных.

В фреймворке Chimera используются 2D-SSM для моделирования многомерных временных рядов, где первая ось соответствует размерности времени, а вторая ось — переменным. Соответственно, каждое состояние является функцией как времени, так и переменных. Первый этап заключается в преобразовании непрерывной формы 2D-SSM в дискретную, учитывая размер шага Δ1 и Δ2, которые представляют собой разрешение исходного сигнала по осям. Используя метод Zero-Order Hold (ZOH), можно дискретизировать исходные данные как:

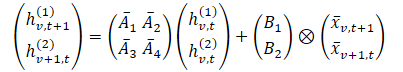
Где t и v используются для указания индекса по размерностям времени и анализируемых переменных, соответственно. Данное выражение можно представить в более простой форме.

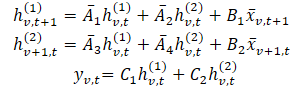
В этой формулировке, интуитивно, hv,t(1) — скрытое состояние, несущее информацию во времени (каждое состояние зависит от его предыдущей временной метки, но в пределах одного и того же признака), где A1 и A2 контролируют акцент на прошедшей кросс-временной и кросс-вариационной информации, соответственно. Аналогично hv,t(2) — это скрытое состояние, которое несет информацию о кросс-вариациях (каждое состояние зависит от других переменных, но с одной и той же временной меткой).

Данные временных рядов часто выбираются из лежащего в основе непрерывного процесса. В этих случаях переменную Δ1 в дискретизации оси времени можно интерпретировать, как разрешение или частоту дискретизации из лежащих в основе непрерывных данных. Однако дискретизация по оси переменных, которая является дискретной по своей природе, является процессом не интуитивным, и вызывает вопросы о его значимости. Шаг дискретизации в 1D-SSM имеет глубокие связи с механизмами врат RNN, автоматически обеспечивая нормализацию модели, и приводит к желаемым свойствам, таким как инвариантность разрешения.

Двухмерная дискретная SSM, представленная параметрами ({Ai}, {Bi}, {Ci}, kΔ1, ℓΔ2) развивается со скоростью в k раз быстрее, чем 2D дискретный SSM с параметрами ({Ai}, {Bi}, {Ci}, Δ1ℓΔ2), и в ℓ раз быстрее ({Ai}, {Bi}, {Ci}, kΔ1, Δ2). Следовательно, параметры Δ1 можно рассматривать как контроллер длины зависимостей, которые захватывает модель. То есть, исходя из приведенного выше описания, мы видим дискретизацию по оси времени, как установку разрешения или частоты дискретизации. Малая Δ1 может фиксировать долгосрочный прогресс, а более крупный Δ1 фиксирует сезонные закономерности.

Дискретизацию по оси анализируемых переменных можно рассматривать, как механизм, аналогичный вратам RNN моделей, где Δ2 управляет длиной контекста модели. Большие значения Δ2 означают меньшее контекстное окно, игнорируя другие переменные, в то время как меньшие значения Δ2 означает больший акцент на зависимостях между анализируемыми переменными.

С целью повышения выразительности и способности восстанавливать авторегрессионные процессы модели, скрытые состояния hv,t(1) должны нести информацию о прошлых временных метках. С этой целью во временном измерении авторы фреймворка ограничивают матрицы A1 и A2, которые должны иметь сопутствующую структуру. Кроме того, для A3 и A4 даже более простая структура диагональных матриц эффективна для слияния информации по размерности анализируемых переменных.

Причинно-следственная природа 2D-SSM приводит к ограниченному потоку информации вдоль размерности переменных, поскольку они не упорядочены. Для решения этой проблемы используются два разных модуля для прямого и обратного прохода по измерению признаков.

Подобно эффективным 1D-SSM, независимую от данных формулировку можно рассматривать, как свертку с ядром K. Эта формулировка не только приводит к более быстрому обучению, обеспечивая возможность параллельной обработки, но и связывает Chimera с самыми последними исследованиями современной архитектуры на основе свертки для временных рядов.

Как обсуждалось ранее, параметры A1 и A2 контролируют акцент на прошлой кросс-временной и кросс-вариационной информации. Аналогично параметры Δ1 и B1 управляют акцентом на текущих и исторических исходных данных. Поскольку эти параметры не зависят от данных, их можно интерпретировать как глобальную особенность системы. Однако, в сложных системах акцент зависит от текущего исходного сигнала. Поэтому необходимо, чтобы эти параметры были функцией исходных данных. Анализируемая зависимость параметров позволяет модели выбирать релевантную и фильтровать нерелевантную информацию для каждого набора исходных данных, обеспечивая механизм, аналогичный Transformer. Кроме того, в зависимости от данных, модель должна адаптивно обучаться полезно смешивать информацию по вариациям. Если сделать параметры зависимыми от исходных данных, это еще больше решает эту проблему и позволяет модели смешивать релевантные и фильтровать нерелевантные параметры для моделирования интересующей переменной. Одним из основных технических вкладов Chimera является построение Bi, Ci и Δi функцией от исходных данных 𝐱v,t.

Фреймворк Chimera использует стек 2D-SSM с нелинейностью между ними. Для усиления выразительности и возможности вышеупомянутых 2D-SSM, подобно моделям глубоких SSM, допускается обучение всех параметров, и в каждом слое используется несколько 2D-SSM, каждый из которых имеет свою ответственность.

Chimera следует широко используемому разложению временных рядов и разлагает их на трендовые компоненты и сезонные паттерны. Тем не менее, он использует специальные черты 2D-SSM для фиксации этих терминов.

Авторская визуализация фреймворка Chimera представлена ниже.

Авторская визуализация фреймворка Chimera

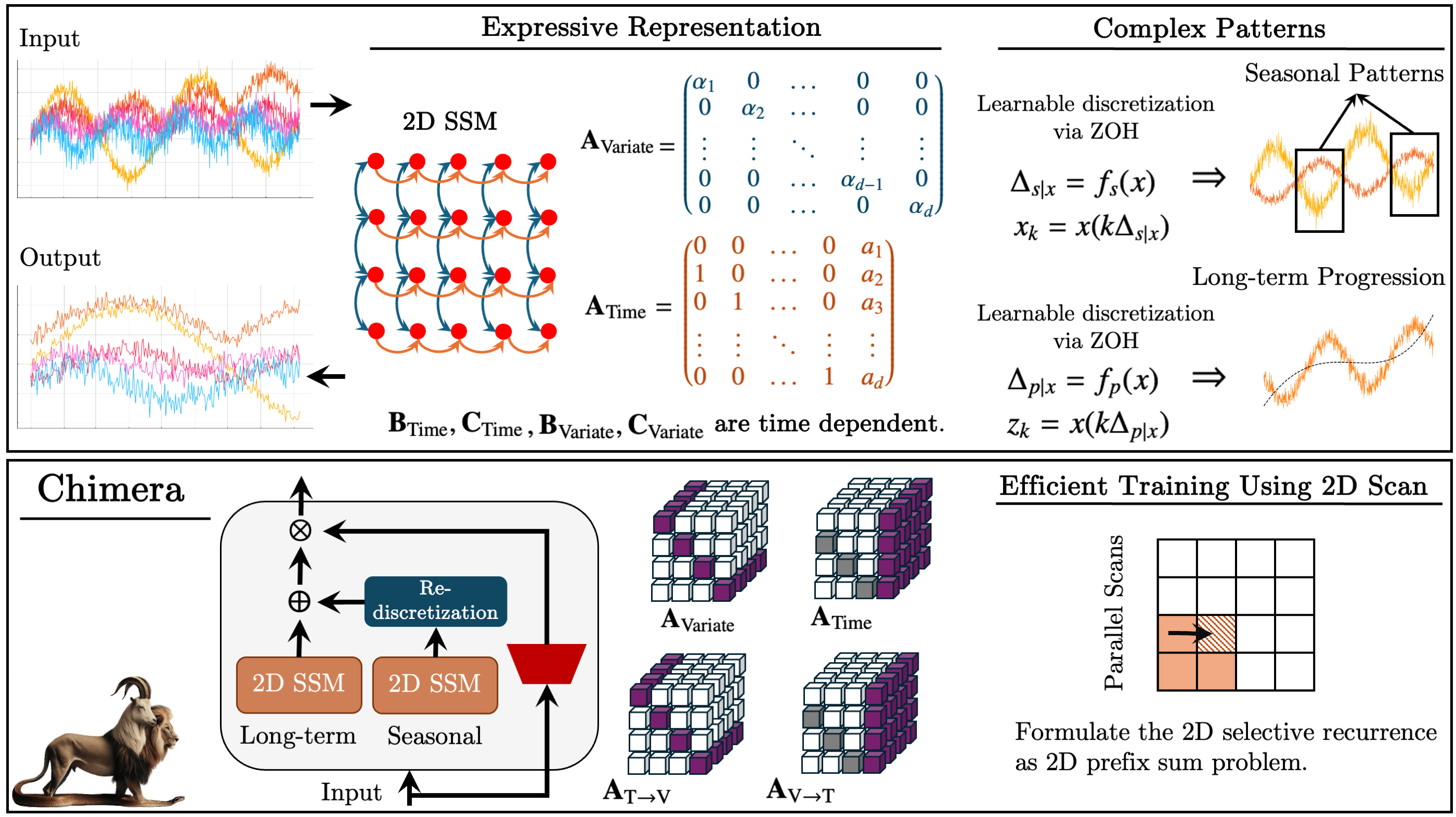
Реализация средствами MQL5

После рассмотрения теоретических аспектов фреймворка Chimera, мы переходим к практическому воплощению собственного видения предложенных подходов. В данном разделе мы рассмотрим интерпретацию предложенной концепции, используя возможности языка программирования MQL5. Однако, прежде чем приступить к программной реализации, необходимо тщательно спроектировать архитектуру модели, чтобы обеспечить её гибкость, эффективность и адаптивность к различным видам данных.

Архитектурные решения

Одними из ключевых компонентов фреймворка Chimera являются матрицы акцента скрытого состояния A{1,…,4}. Авторы фреймворка предложили использовать диагональные матрицы с дополнением, что снижает число обучаемых параметров и уменьшает вычислительную сложность. Такой подход позволяет существенно сократить потребление ресурсов и ускорить процесс обучения модели.

Однако, у данного решения есть и недостатки. Использование диагональных матриц накладывает существенные ограничения на модель, так как она способна анализировать только локальные зависимости между последующими элементами последовательности. Это ограничивает её выразительность и способность выявлять сложные закономерности. В связи с этим, в своей интерпретации мы используем полностью обучаемые матрицы. Такой подход увеличивает число параметров, но значительно расширяет адаптивность модели, позволяя учитывать более сложные зависимости в анализируемых данных.

При этом наш вариант матриц сохраняет ключевую концепцию оригинального решения — они не зависят напрямую от исходных данных и обучаются. Это позволяет модели становиться более универсальной, что особенно важно для решения различных задач анализа многомерных временных последовательностей.

Другим важным аспектом является интеграция этих матриц в процесс вычислений. Как было показано в теоретической части, матрицы акцента умножаются на скрытые состояния модели, что соответствует принципам работы нейронных слоев. Учитывая это, мы предлагаем реализовать их в виде сверточного слоя нейросети, где матрица акцента будет представлять собой обучаемый тензор параметров. Интеграция в стандартные нейросетевые архитектуры позволяет задействовать реализованные ранее алгоритмы оптимизации.

Более того, для возможности организации процесса параллельного вычисления сразу четырех матриц акцентов было принято решение об объединении их в единый конкатенированный тензор, что, в свою очередь, потребовало объединения двух матриц скрытого состояния в единый тензор.

Несмотря на все преимущества данного подхода, он оказывается недостаточно универсальным для работы с другими параметрическими матрицами в 2D-SSM. Одним из ограничений является фиксированность структуры матриц, что снижает гибкость модели при обработке сложных многомерных данных. В связи с этим, для повышения выразительной способности модели мы используем контекстно-зависимые матрицы Bi, Ci и Δi, которые способны динамически адаптироваться к исходным данным, обеспечивая более глубокий анализ временных зависимостей.

Контекстно-зависимые матрицы формируются на основе информации, полученной из исходных данных, что позволяет учитывать их структуру и варьировать параметры модели в зависимости от характеристик анализируемой последовательности. Этот подход даёт модели возможность не только анализировать локальные взаимосвязи, но и учитывать глобальные тренды, что особенно важно для задач прогнозирования и работы с временными рядами.

Следуя рекомендациям авторов фреймворка, мы реализуем эти матрицы посредством специализированных нейронных слоёв, отвечающих за адаптацию параметров в зависимости от контекста.

На следующем этапе важной задачей является организация процесса сложного взаимодействия данных внутри 2D-SSM модели. Это требует эффективного управления вычислительными ресурсами, поскольку сложные многомерные структуры данных нуждаются в оптимизированном подходе к обработке. С учётом требований к вычислительной эффективности и быстродействию системы, было принято решение о вынесении данного блока операций в отдельный кернел, работающий на стороне OpenCL-программы.

Такой подход даёт несколько значительных преимуществ. Во-первых, он позволяет существенно сократить задержки при обработке данных за счёт параллельного выполнения операций на графическом процессоре. Это критически важно при анализе больших объемов информации, где последовательная обработка может привести к значительным временным затратам. Во-вторых, за счёт аппаратного ускорения OpenCL можно эффективно распараллелить вычисления, что даёт возможность обрабатывать сложные временные ряды в реальном времени.

Дополнение OpenCL-программы

После детального проектирования архитектуры реализуемых подходов, следующим шагом становится её реализация в коде. В первую очередь необходимо внести изменения в OpenCL-программу, чтобы оптимизировать выполнение вычислительных операций и обеспечить эффективное взаимодействие с основными компонентами модели. Мы создадим алгоритм сложного взаимодействия обучаемых параметров 2D-SSM и исходных данных в кернеле SSM2D_FeedForward.

В параметрах метода мы передаем указатели на буфера данных, содержащих все необходимые параметры модели и проекции исходных данных в контексте времени и анализируемых переменных.

__kernel void SSM2D_FeedForward(__global const float *ah,
                                __global const float *b_time,
                                __global const float *b_var,
                                __global const float *px_time,
                                __global const float *px_var,
                                __global const float *c_time,
                                __global const float *c_var,
                                __global const float *delta_time,
                                __global const float *delta_var,
                                __global       float *hidden,
                                __global       float *y
                               )
  {
   const size_t n = get_local_id(0);
   const size_t d = get_global_id(1);
   const size_t n_total = get_local_size(0);
   const size_t d_total = get_global_size(1);

В теле кернела мы, как обычно, сначала идентифицируем текущий поток в двухмерном пространстве задач. Первое измерение соответствует количеству элементов последовательности, а второе — размерности признаков. При этом мы объединяем в рабочие группы все элементы последовательности одного признака.

Здесь стоит обратить внимание, что проекции обучаемых параметров и исходных данных в контексте времени и анализируемых индикаторов должны быть приведены в сопоставимый вид на этапе подготовки данных до передачи в кернел.

Далее мы определяем скрытое состояние в обоих контекстах с учетом обновленной информации. Полученные значения мы сохраняем в соответствующий буфер данных.

//--- Hidden state
   for(int h = 0; h < 2; h++)
     {
      float new_h = ah[(2 * n + h) * d_total + d] + ah[(2 * n_total + 2 * n + h) * d_total + d];
      if(h == 0)
         new_h += b_time[n] * px_time[n * d_total + d];
      else
         new_h += b_var[n] * px_var[n * d_total + d];
      hidden[(h * n_total + n)*d_total + d] = IsNaNOrInf(new_h, 0);
     }
   barrier(CLK_LOCAL_MEM_FENCE);

После выполнения операций, мы должны синхронизировать потоки рабочей группы, так как для выполнения дальнейших операций нам потребуются результаты всей рабочей группы.

Следующим этапом мы определяем результат работы модели. Для этого нам необходимо умножить матрицы контекста и дискретизации на вычисленное выше скрытое состояние. С целью выполнения данной операции, мы организовываем цикл, в теле которого осуществляем умножение соответствующих элементов матриц в контексте времени и анализируемых переменных. Результаты операций обоих контекстов суммируем.

//--- Output
   uint shift_c = n;
   uint shift_h1 = d;
   uint shift_h2 = shift_h1 + n_total * d_total;
   float value = 0;
   for(int i = 0; i < n_total; i++)
     {
      value += IsNaNOrInf(c_time[shift_c] * delta_time[shift_c] * hidden[shift_h1], 0);
      value += IsNaNOrInf(c_var[shift_c] * delta_var[shift_c] * hidden[shift_h2], 0);
      shift_c += n_total;
      shift_h1 += d_total;
      shift_h2 += d_total;
     }

И теперь нам остается перенести полученное значение в соответствующий элемент глобального буфера результатов и завершить работу кернела.

//---
   y[n * d_total + d] = IsNaNOrInf(value, 0);
  }

Далее нам предстоит организовать алгоритмы обратного прохода. Оптимизировать параметры мы будем средствами соответствующих нейронных слоев. А вот для распределения градиента ошибки между ними, создадим кернел SSM2D_CalcHiddenGradient, в теле которого построим алгоритм, обратный приведенному выше.

В параметрах кернела мы передаем указатели на тот же набор матриц, дополнив его буферами градиентов ошибки. Для исключения путаницы в большом количестве буферов мы используем префикс grad_ для буферов соответствующих градиентов ошибки.

__kernel void SSM2D_CalcHiddenGradient(__global const float *ah,
                                       __global       float *grad_ah,
                                       __global const float *b_time,
                                       __global       float *grad_b_time,
                                       __global const float *b_var,
                                       __global       float *grad_b_var,
                                       __global const float *px_time,
                                       __global       float *grad_px_time,
                                       __global const float *px_var,
                                       __global       float *grad_px_var,
                                       __global const float *c_time,
                                       __global       float *grad_c_time,
                                       __global const float *c_var,
                                       __global       float *grad_c_var,
                                       __global const float *delta_time,
                                       __global       float *grad_delta_time,
                                       __global const float *delta_var,
                                       __global       float *grad_delta_var,
                                       __global const float *hidden,
                                       __global const float *grad_y
                                      )
  {
//---
   const size_t n = get_global_id(0);
   const size_t d = get_local_id(1);
   const size_t n_total = get_global_size(0);
   const size_t d_total = get_local_size(1);

Запуск данного кернела планируется в том же пространстве задач, что и кернел прямого прохода. Однако, в данном случае, мы объединяем потоки в рабочие группы по пространству признаков.

Перед началом работ мы инициализируем ряд локальных переменных, в которых будем сохранять промежуточные значения и смещения в буферах данных.

//--- Initialize indices for data access
   uint shift_c = n;
   uint shift_h1 = d;
   uint shift_h2 = shift_h1 + n_total * d_total;
   float grad_hidden1 = 0;
   float grad_hidden2 = 0;

Затем, организуем цикл распределения градиента ошибки от буфера результатов до скрытого состояния, а так же матриц контекста и дискретизации, в соответствии с их влиянием на итоговый результат работы модели. Одновременно распределяем градиент ошибки в контекстах времени и анализируемых переменных.

//--- Backpropagation: compute hidden gradients from y
   for(int i = 0; i < n_total; i++)
     {
      float grad = grad_y[i * d_total + d];
      float c_t = c_time[shift_c];
      float c_v = c_var[shift_c];
      float delta_t = delta_time[shift_c];
      float delta_v = delta_var[shift_c];
      float h1 = hidden[shift_h1];
      float h2 = hidden[shift_h2];
      //-- Accumulate gradients for hidden states
      grad_hidden1 += IsNaNOrInf(grad * c_t * delta_t, 0);
      grad_hidden2 += IsNaNOrInf(grad * c_v * delta_v, 0);
      //--- Compute gradients for c_time, c_var, delta_time, delta_var
      grad_c_time[shift_c] += grad * delta_t * h1;
      grad_c_var[shift_c]  += grad * delta_v * h2;
      grad_delta_time[shift_c] += grad * c_t * h1;
      grad_delta_var[shift_c]  += grad * c_v * h2;
      //--- Update indices for the next element
      shift_c += n_total;
      shift_h1 += d_total;
      shift_h2 += d_total;
     }

Далее мы распределим градиент ошибки на матрицы акцентов.

//--- Backpropagate through hidden -> ah, b_time, px_time
   for(int h = 0; h < 2; h++)
     {
      float grad_h = (h == 0) ? grad_hidden1 : grad_hidden2;
      //--- Store gradients in ah (considering its influence on two elements)
      grad_ah[(2 * n + h) * d_total + d] = grad_h;
      grad_ah[(2 * (n_total + n) + h) * d_total + d] = grad_h;
     }

И передадим на проекции исходных данных.

//--- Backpropagate through px_time and px_var (influenced by b_time and b_var)
   grad_px_time[n * d_total + d] = grad_hidden1 * b_time[n];
   grad_px_var[n * d_total + d] = grad_hidden2 * b_var[n];

А вот градиент ошибки по матрице Bi нам предстоит собрать по всем измерениям. Поэтому мы сначала обнулим значение соответствующего буфера градиентов ошибки и синхронизируем потоки рабочей группы.

   if(d == 0)
     {
      grad_b_time[n] = 0;
      grad_b_var[n] = 0;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

А затем суммируем значения отдельных потоков рабочей группы.

//--- Sum gradients over all d for b_time and b_var
   grad_b_time[n] += grad_hidden1 * px_time[n * d_total + d];
   grad_b_var[n] += grad_hidden2 * px_var[n * d_total + d];
  }

Результаты операций передаем в соответствующие глобальные буфера данных и завершаем работу кернела.

На этом мы завершаем работу на стороне OpenCL-программы. С полным её кодом вы можете самостоятельно ознакомиться во вложении.

Объект 2D-SSM

После завершения этапа работы на стороне OpenCL, следующим шагом переходим к построению 2D-SSM структуры на стороне основной программы. Для этого мы создадим класс CNeuron2DSSMOCL, в рамках которого реализуем необходимые алгоритмы. Структура нового класса представлена ниже.

class CNeuron2DSSMOCL  :  public CNeuronBaseOCL
  {
protected:
   uint                 iWindowOut;
   uint                 iUnitsOut;
   CNeuronBaseOCL       cHiddenStates;
   CLayer               cProjectionX_Time;
   CLayer               cProjectionX_Variable;
   CNeuronConvOCL       cA;
   CNeuronConvOCL       cB_Time;
   CNeuronConvOCL       cB_Variable;
   CNeuronConvOCL       cC_Time;
   CNeuronConvOCL       cC_Variable;
   CNeuronConvOCL       cDelta_Time;
   CNeuronConvOCL       cDelta_Variable;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForwardSSM2D(void);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradientsSSM2D(void);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuron2DSSMOCL(void)  {};
                    ~CNeuron2DSSMOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuron2DSSMOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      Clear(void) override;
  };

В представленной структуре объекта мы видим уже знакомый нам набор виртуальных переопределяемых методов и довольно большое количество внутренних объектов. Думаю, что количество объектов не было неожиданным. Оно продиктовано архитектурой модели. И отчасти, о назначении объектов можно догадаться, исходя из их наименования. Ну а более подробно описание функционала каждого объекта будет представлено в процессе реализации алгоритмов построения методов нашего класса.

Все внутренние объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Преимущества такого подхода мы уже не раз обсуждали. А инициализация всех объявленных и унаследованных объектов осуществляется в методе Init.

bool CNeuron2DSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window_in, uint window_out, uint units_in, uint units_out,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_out,
                                                       optimization_type, batch))
      return false;
   SetActivationFunction(None);

В параметрах метода мы получаем ряд констант, которые позволяют однозначно определить архитектуру создаваемого объекта. Среди них можно выделить размерности исходных данных и ожидаемого результата ({units_in, window_in} и {units_out, window_out}, соответственно).

В теле метода, как обычно, сначала вызываем одноименный метод родительского класса, которому передадим размерности ожидаемого результата. В методе родительского класса уже реализован необходимый блок контролей и алгоритмы инициализации унаследованных объектов и интерфейсов. Поэтому, после успешного выполнения операций метода родительского класса мы смело сохраняем размерности тензора результатов во внутренние переменные.

   iWindowOut = window_out;
   iUnitsOut = units_out;

Как было сказано выше, при построении кернелов на стороне OpenCL-программы, проекции исходных данных обоих контекстов должны иметь сопоставимый вид. В своей реализации мы приводим их к размерности тензора результатов. Вначале создадим модель проекции исходных данных в контексте времени.

С целью сохранения информации унитарных последовательностей многомерного временного ряда первой осуществляем независимую проекцию одномерных последовательностей до заданного размера. И здесь следует вспомнить, что на вход мы получаем данные в виде матрицы, строки которой соответствуют временным шагам. Следовательно, для удобства работы с унитарными последовательностями нам необходимо сначала транспонировать полученную матрицу исходных данных.

//---
   int index = 0;
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeOCL *transp = NULL;
//--- Projection Time
   cProjectionX_Time.Clear();
   cProjectionX_Time.SetOpenCL(OpenCL);
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) ||
      !cProjectionX_Time.Add(transp))
     {
      delete transp;
      return false;
     }

И только потом мы можем воспользоваться средствами сверточного слоя для изменения размерности унитарных последовательностей.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, iUnitsOut, window_in, 1,
                                                       optimization, iBatch) ||
      !cProjectionX_Time.Add(conv))
     {
      delete conv;
      return false;
     }

Далее нам необходимо осуществить проекцию данных по измерению признаков. Для это осуществляем обратное транспонирование данных.

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, window_in, iUnitsOut, optimization, iBatch) ||
      !cProjectionX_Time.Add(transp))
     {
      delete transp;
      return false;
     }

И осуществляем проекцию данных с помощью сверточного слоя.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, iWindowOut, iUnitsOut, 1,
                                                          optimization, iBatch) ||
      !cProjectionX_Time.Add(conv))
     {
      delete conv;
      return false;
     }

Аналогичным образом мы осуществляем проекцию данных в контексте признаков. Только на этот раз, мы вначале делаем проекцию по оси переменных, а затем транспонируем данные и осуществляем проекцию по оси времени.

//--- Projection Variables
   cProjectionX_Variable.Clear();
   cProjectionX_Variable.SetOpenCL(OpenCL);
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, iUnitsOut, units_in, 1,
                                                        optimization, iBatch) ||
      !cProjectionX_Variable.Add(conv))
     {
      delete conv;
      return false;
     }

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, iUnitsOut, optimization, iBatch) ||
      !cProjectionX_Variable.Add(transp))
     {
      delete transp;
      return false;
     }

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, iWindowOut, iUnitsOut, 1,
                                                        optimization, iBatch) ||
      !cProjectionX_Variable.Add(conv))
     {
      delete conv;
      return false;
     }

После инициализации моделей проекции исходных данных, переходим к работе с другими внутренними объектами. Здесь мы вначале инициализируем объект скрытого состояния. Данный объект используется только для хранения данных и не содержит обучаемых параметров. Однако, он должен быть достаточного объема для хранения данных скрытого состояния обоих контекстов.

//--- HiddenState
   index++;
   if(!cHiddenStates.Init(0, index, OpenCL, 2 * iUnitsOut * iWindowOut, optimization, iBatch))
      return false;

Далее мы переходим к матрицам акцентов скрытого состояния. Как было сказано выше, мы реализуем все 4 матрицы в рамках одного сверточного слоя. Это позволяет нам осуществлять их параллельную работу.

Здесь следует обратить внимание, что на выходе данного слоя мы ожидаем получить умножения скрытого состояния на 4 независимые матрицы. При этом две из них работают с контекстом времени, а другие — с контекстом признаков. С целью получения желаемого эффекта, мы объявляем сверточный слой с количеством фильтров в 2 раза больше окна исходных данных, что соответствует двум матрицам акцентов. И указываем работу сверточного слоя с двумя независимыми последовательностями, что соответствует контекстам времени и признаков. Напомню, что для независимых последовательностей сверточный слой использует различные матрицы фильтров. Таким образом мы получаем 4 матрицы акцентов, которые попарно работают с различными контекстами.

//--- A*H
   index++;
   if(!cA.Init(0, index, OpenCL, iWindowOut, iWindowOut, 2 * iWindowOut, iUnitsOut, 2,
                                                                optimization, iBatch))
      return false;

Здесь стоит обратить внимание, что большие параметры акцентов могут привести к эффекту взрыва градиентов ошибки. Поэтому мы в 10 раз уменьшаем параметры после случайно инициализации.

if(!SumAndNormilize(cA.GetWeightsConv(), cA.GetWeightsConv(), cA.GetWeightsConv(),
                                               iWindowOut, false, 0, 0, 0, 0.05f))
   return false;

Следующим этапом мы переходим к генерации адаптивных контекстно-зависимых матриц Bi, Ci и Δi, которые в нашей реализации являются функциями от исходных данных. Для их генерации мы воспользуемся сверточными слоями, которые на вход получают проекции исходных данных соответствующего контекста, а на выходе генерирую необходимую матрицу.

//--- B
   index++;
   if(!cB_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, 
                                                         optimization, iBatch))
      return false;
   cB_Time.SetActivationFunction(TANH);
   index++;
   if(!cB_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, 
                                                            optimization, iBatch))
      return false;
   cB_Variable.SetActivationFunction(TANH);

Предложенный подход аналогичен вратам в RNN. И мы используем гиперболический тангенс в качестве функций активации для матриц Bi и Ci, подчеркивая возможность положительной и отрицательной зависимости.

//--- C
   index++;
   if(!cC_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                optimization, iBatch))
      return false;
   cC_Time.SetActivationFunction(TANH);
   index++;
   if(!cC_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                    optimization, iBatch))
      return false;
   cC_Variable.SetActivationFunction(TANH);

Матрица Δi выполняет функции обучаемой дискретизации и не может содержать отрицательных значений. Для неё мы используем SoftPlus в качестве функции активации, который является гладким аналогом ReLU.

//--- Delta
   index++;
   if(!cDelta_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                    optimization, iBatch))
      return false;
   cDelta_Time.SetActivationFunction(SoftPlus);
   index++;
   if(!cDelta_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                        optimization, iBatch))
      return false;
   cDelta_Variable.SetActivationFunction(SoftPlus);
//---
   return true;
  }

После инициализации всех внутренних объектов, нам остается лишь вернуть логический результат выполнения операций вызывающей программе и завершить работу метода.

Мы хорошо сегодня потрудились, но наша работа ещё не завершена. Предлагаю сделать небольшой перерыв и продолжить в следующей статье. В ней мы завершим построение необходимых объектов, интегрируем их в модель и проверим эффективность реализованных подходов на реальных исторических данных.

Заключение

В данной статье мы познакомились с фреймворком двухмерной модели пространства состояний Chimera, которая предлагает новые подходы для моделирования многомерных временных рядов с учетом зависимостей в контексте времени и признаков. Chimera использует двухмерные модели пространства состояний (2D-SSM), что позволяет ей эффективно моделировать как долгосрочные прогрессии, так и сезонные паттерны.

В практической части мы начали работу по имплементации собственного видения предложенных подходов средствами MQL5. Однако, начатая работа ещё не завершена. В следующей статье мы продолжим построение предложенных подходов и обязательно проверим эффективность реализованных решений на реальных исторических данных.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2458.91 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Переосмысливаем классические стратегии (Часть IV): SP500 и казначейские облигации США

В этой серии статей мы анализируем классические торговые стратегии с использованием современных алгоритмов, чтобы определить, можно ли улучшить стратегию с помощью искусственного интеллекта (ИИ). В сегодняшней статье мы рассмотрим классический подход к торговле индексом SP500, используя его взаимосвязь с казначейскими облигациями США (US Treasury Notes).

Разработка системы репликации (Часть 67): Совершенствуем индикатор управления

В данной статье мы рассмотрим, чего можно добиться с помощью небольшой доработки кода. Данная доработка направлена на упрощение нашего кода, более активное использование вызовов библиотеки MQL5 и, прежде всего, на то, чтобы сделать его гораздо более стабильным, безопасным и простым для использования в другом коде, который мы будем разрабатывать в будущем.

Фибоначчи на Форекс (Часть I): Проверяем отношения цены и времени

Как рынок ходит по отношениям, основанным на числах Фибоначчи? Эта последовательность, где каждое следующее число равно сумме двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21...), не только описывает рост популяции кроликов. Рассмотрим гипотезу Пифагора о том, что все в мире подчиняется определенным соотношениям чисел...

Упрощаем торговлю на новостях (Часть 3): Совершаем сделки

В этой статье наш советник новостной торговли начнет открывать сделки на основе экономического календаря, хранящегося в нашей базе данных. Кроме того, мы улучшим графику советника, чтобы отображать более актуальную информацию о предстоящих событиях экономического календаря.