Матричная факторизация: моделирование, которое более практично

Введение

Приветствую всех! Моя новая статья сфокусирована на образовательном контенте.

В предыдущей статье "Факторизация матриц: основы" я немного рассказал о том, как вы, мои дорогие читатели, можете использовать матрицы в своих общих вычислениях. Однако в тот раз я хотел, чтобы вы понимали, как производятся вычисления, поэтому не уделял слишком много внимания созданию правильной модели матриц.

Вы могли не заметить, что моделирование матриц оказалось немного странным, так как указывались не строки и столбцы, а только столбцы. Это выглядит очень странно при чтении кода, выполняющего матричные факторизации. Если вы ожидали увидеть указанные строки и столбцы, то могли бы запутаться при попытке выполнить факторизацию.

Более того, данный способ моделирования матриц не самый лучший. Это связано с тем, что при моделировании матриц таким образом, мы сталкиваемся с некими ограничениями, которые заставляют нас использовать другие методы или функции, которые не были бы необходимы, если бы моделирование осуществлялось более подходящим способом.

Поскольку процедура хоть и несложная, но для ее правильного применения необходимо хорошо в ней разбираться, я предпочел не вдаваться в подробности в предыдущей статье. В данной статье мы рассмотрим всё более спокойно, без спешки, чтобы ни в коем случае не передать вам неверные мысли о моделировании матриц, чтобы их можно было правильно факторизовать.

Матрицы, по сути своей, являются лучшим способом выполнения некоторых видов вычислений, так как требуют минимум дополнительных реализаций с нашей стороны. Но именно по этой причине следует проявлять большую осторожность при реализации чего-либо в матрицах. В отличие от обычного моделирования, если мы неправильно смоделируем что-то в матрицах, то получим довольно странные результаты или, в лучшем случае, столкнемся с большими трудностями при сопровождении разработанного кода.

Меры предосторожности при моделировании матрицы

Вы могли бы задаться вопросом: почему автор сказал, что моделирование в предыдущей статье было странным, ведь для меня всё понятно. Мне кажется теперь всё ясно. Ну что ж, уважаемый читатель, давайте посмотрим на фрагмент кода из предыдущей статьи, в котором моделировались матрицы. Возможно, так будет чуть понятнее, что я хочу вам показать. Фрагмент можно увидеть ниже.

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2] = {
24.                            cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                           -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                         },
27.            M_2[][2]  =  {
28.                            0.0,  0.0,
29.                            1.5, -.75,
30.                            1.0,  0.0,
31.                            1.5,  .75
32.                         },
33.            M_3[M_2.Size() / 2][2];

Хотя это и работает, как видно из фрагмента, но вопрос довольно запутанный. Это трудно понять. Будьте внимательны, когда мы пишем многомерный массив в коде, мы используем следующую конфигурацию:

Метка [Dimension_01][Dimension_02]....[Dimension_N];

Несмотря на то, что в общем виде код может показаться простым, этот тип нотации сложен для понимания, когда применяется к области факторизации матриц. Это связано с тем, что при работе с матрицами такой способ выражения в многомерном массиве вносит путаницу. Скоро вы поймете причину. Чтобы сделать проще, мы сведем данное понятие к двумерной системе, т.е. только к строкам и столбцам. Однако матрицы могут иметь любое количество измерений. Если упростить до двумерной матрицы, то обозначение будет выглядеть так:

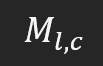
Что это значит? Буква "M" означает название матрицы, "l" - количество строк, а "c" - количество столбцов. В общих чертах, при обращении к элементу матрицы мы будем использовать ту же самую нотацию, которая выглядит так:

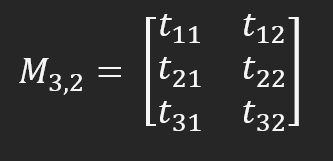
Обратите внимание, что матрица M теперь состоит из шести элементов, доступ к которым можно получить с помощью системы строк и столбцов. Но посмотрите внимательно на предыдущее изображение - на что это похоже? В зависимости от вашего опыта, может выглядеть по-разному. Однако, чем бы это было в терминологии программирования? Итак, это двумерный массив. Но при таком подходе матрица выглядит статичной. Матрица - это динамическая сущность; ее можно читать по-разному, в зависимости от того, что мы вычисляем. В некоторых случаях её нужно читать по диагонали, в других - столбец за столбцом, а в третьих - строка за строкой. Таким образом, представление о матрице как о многомерном массиве превращает нечто динамическое в нечто статическое. Это усложняет реализацию некоторых матричных вычислений.

Однако мы здесь не для того, чтобы изучать азы программирования. Я здесь для того, чтобы показать вам, моим дорогим читателям, как можно визуализировать любую матрицу наилучшим образом, позволяя ей оставаться динамичной сущностью, какой она и должна быть.

Таким образом, представление о матрице как о массиве не является неверным. Проблема возникает при её рассмотрении как многомерного массива. В идеале нужно воспринимать матрицу как одномерный массив, но без фиксированного числа измерений. То, что вы сейчас прочитали звучит странно, но проблема кроется в языке. В настоящее время не существует подходящих терминов или выражений для описания некоторых понятий.

Вспомните, с какими трудностями пришлось столкнуться Исааку Ньютону, когда он впервые объяснял свои вычисления. Должно быть, это было довольно сложно из-за отсутствия подходящих терминов для некоторых понятий. Но давайте вернемся к нашему вопросу.

У нас уже есть способ представить матрицу как массив. Но теперь возникает первая проблема: как отсортировать элементы в массиве? Если вы не понимаете, почему это является проблемой, значит вы не понимаете всего того, что связано с факторизацией матриц. От того, как будут упорядочены элементы, в значительной степени будет зависеть то, как будет реализован код факторизации. Хотя результаты в обоих случаях одинаковы, нам может понадобиться больше или меньше переходов внутри массива, чтобы получить правильный результат. Это связано именно с тем, что память компьютера линейна. Если мы упорядочим элементы следующим образом: t11, t12, t21, t22, t31 и t32, что вполне уместно во многих случаях, нам придется сделать так, чтобы переходы обращались к элементам в другом порядке, это будет необходимо для выполнения определенного расчета. И это, несомненно, произойдет, что бы мы ни делали.

Обычно, когда мы сортируем элементы массива, мы делаем это, читая строку за строкой. Но ничто не мешает нам делать это и по-другому, например, читать колонку за колонкой или иным способом на ваше усмотрение. Не стесняйтесь делать это так, как вам удобно.

После этого возникает еще одна небольшая проблема, но она связана не с программированием, а с тем, как производится факторизация матрицы. В данном случае я не буду вдаваться в подробности. Причина проста: то, как мы справимся с этим, зависит от того, как мы реализовали матрицу или какой вид матрицы мы используем. Я рекомендую изучить книги или математическую литературу, чтобы понять, как реализовать решение проблем, которые могут возникнуть, и правильно выполнить факторизацию. Однако реализация кода никогда не бывает сложной, ведь код - это самая легкая часть работы. Самое сложное - понять, как будет выполняться факторизация. Примером может служить вычисление определителя матрицы, изображенной на предыдущей рисунке. Обратите внимание, что это не квадратная матрица, и построение определителя в этом случае немного отличается от того, что мы делали бы в случае квадратной матрицы. Как уже было сказано, нужно изучать математическую часть, поскольку каждый конкретный случай может потребовать особого подхода.

Запутанное дело

Хорошо, теперь, когда всё немного объяснено и выровнено, можно перейти к этапу написания кода. Давайте продолжим работу с примером, рассмотренным в предыдущей статье, поскольку он довольно практичен и прост для понимания. Кроме того, на этом примере легко показать еще одно преимущество использования матричных вычислений в некоторых ситуациях. Давайте вспомним, как выглядел код. Это можно сделать, посмотрев на приведенный ниже код.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[][], const double &B[][], double &R[][], const int nDim)
13. {
14.     for (int c = 0, size = (int)(B.Size() / nDim); c < size; c++)
15.     {
16.         R[c][0] = (A[0][0] * B[c][0]) + (A[0][1] * B[c][1]);
17.         R[c][1] = (A[1][0] * B[c][0]) + (A[1][1] * B[c][1]);
18.     }
19. }
20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2]{
24.                         cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                         -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                     },
27.            M_2[][2] {
28.                         0.0,  0.0,
29.                         1.5, -.75,
30.                         1.0,  0.0,
31.                         1.5,  .75
32.                     },
33.            M_3[M_2.Size() / 2][2];
34. 
35.     int dx[M_2.Size() / 2], dy[M_2.Size() / 2];
36.     
37.     MatrixA_x_MatrixB(M_1, M_2, M_3, 2);
38.     ZeroMemory(M_1);
39.     M_1[0][0] = M_1[1][1] = size;
40.     MatrixA_x_MatrixB(M_1, M_3, M_2, 2);
41. 
42.     for (int c = 0; c < (int)M_2.Size() / 2; c++)
43.     {
44.         dx[c] = x + (int) M_2[c][0];
45.         dy[c] = y + (int) M_2[c][1];
46.     }
47. 
48.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
49.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
50. }
51. //+------------------------------------------------------------------+
52. int OnInit()
53. {    
54.     int px, py;
55.     
56.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
60.     canvas.Erase(ColorToARGB(clrWhite, 255));
61.         
62.     Arrow(px / 2, py / 2, 160);
63. 
64.     canvas.Update(true);
65.     
66.     return INIT_SUCCEEDED;
67. }
68. //+------------------------------------------------------------------+
69. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
70. {
71.     return rates_total;
72. }
73. //+------------------------------------------------------------------+
74. void OnDeinit(const int reason)
75. {
76.     canvas.Destroy();
77. }
78. //+------------------------------------------------------------------+

Поскольку данный код был описан в предыдущей статье, а также доступен в приложении к ней, мы не повторим его здесь. Мы сосредоточимся только на том фрагменте, с которым действительно нужно работать, то есть на процедуре Arrow и процедуре MatrixA_x_MatrixB, которые действительно что-то делают в нашем демонстрационном коде.

Для начала давайте изменим способ создания массивов. На самом деле изменения будут более простыми и тонкими, чем может показаться, но они всё равно поменяют то, как мы должны будем начать работу.

Для начала возьмем массив M_1, показанный в коде выше. Изучите его, чтобы понять, о чем пойдет речь.

Обратите внимание, здесь есть кое-что интересное, и это как раз относится к теме, о которой говорилось в предыдущем разделе. В строке 23 объявляется массив или матрица M_1 с двумя строками и двумя столбцами. В данном случае в этом нет никаких сомнений. То же самое по отношению к массиву или матрице M_2, у которых нет определения количества строк, но есть определение количества столбцов, количество которых равняется двум. До этого момента не возникает никаких сомнений или проблем; понять то, что мы делаем, довольно просто, поскольку каждая новая строка в коде соответствует новой строке в матрице, а каждый новый столбец в этой строке будет новым столбцом в матрице. Всё очень просто. Однако есть проблема, и она кроется в коде процедуры MatrixA_x_MatrixB. Можете ли вы определить проблему? Нет? Может быть. Возможно, вы это видите, но вам непонятно.

На самом деле, проблема кроется в процедуре MatrixA_x_MatrixB, которая отвечает за перемножение матриц. Так как то, что мы здесь делаем, довольно просто, оно не мешает реализации кода. Однако нам всё равно нужно решать проблему, ведь она существует и тормозит наш прогресс. Как только нам понадобится реализовать более сложное умножение, это станет настоящим препятствием.

Если вы не заметили проблему, обратите внимание на переменную B. Она представляет собой матрицу, которая преумножает другую матрицу. Чтобы лучше представить проблему, давайте сократим матрицу B до одного столбца, но с двумя строками, поскольку матрица A имеет два столбца. Для выполнения умножения, нужно сделать то, что показано на рисунке ниже.

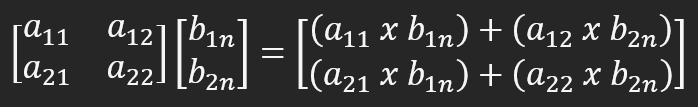
Это даст нам правильный результат. Именно это и происходит при умножении или факторизации матрицы. Для получения более подробной информации я вам предлагаю изучить данный вопрос. В любом случае умножение выполняется по строкам столбца, в результате чего получается значение, которое остается в столбце. Это происходит из-за того, что второй фактор - это столбец. Если умножение выполняется по столбцам, то полученное значение должно быть помещено в виде строк.

Хотя кажется, что всё сказанное может только запутать вас, но на самом деле именно это и есть правило выполнения матричного умножения. Когда другой программист будет анализировать код, он не увидит, что всё делается правильно. Именно эту проблему можно заметить в строках 16 и 17, где должен быть произведен расчет, показанный на рисунке выше. Но обратите внимание, что в матрице A мы используем вычисление по ряду, а в матрице B мы также используем вычисление по ряду. Это сбивает нас с толку, хотя в этом простом примере он предоставляет правильные данные.

Можно подумать: ну и что? Если всё работает, оставьте всё так, как есть. Но дело не в этом. Если в какой-то момент нам понадобится усовершенствовать код, чтобы работать с большей матрицей или охватить несколько иной случай, то в итоге мы сильно усложним задачу, пытаясь заставить работать что-то относительно простое. Так что подобные вещи нужно делать без такой путаницы. Чтобы решить данную проблему, нам нужно отказаться от использования этой модели и принять немного другую. Хотя поначалу всё может показаться запутанным, по крайней мере, оно будет правильным, в точности как показано на рисунке выше.

Чтобы не запутаться, давайте посмотрим, как это сделать в новой теме.

Делаем всё проще

Хотя то, что мы собираемся здесь сделать, может показаться сложным, на самом деле это не так, если делать всё правильно и с должной осторожностью. Мы довольно простым способом сделаем то, что в ином случае было бы гораздо более утомительным. Посмотрите на рисунок ниже.

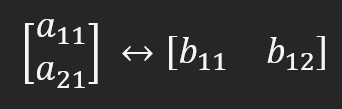
Данное представление показывает, что обе матрицы эквивалентны. Это связано с тем, что матрица с элементами A в левой части является матрицей строк. При преобразовании ее в матрицу с элементами B в правой части, которая в данном случае является матрицей столбцов, нам не потребуется делать много изменений, возможно, только перевернуть или изменить индекс в некоторых случаях. Однако это может понадобиться не один раз: для преобразования матрицы строк в матрицу столбцов и наоборот, для факторизации матриц. Но чтобы всё было правильно, a11 должно быть равно b11, а a21 должно быть равно b12.

В некоторых случаях можно заметить, что нет необходимости вносить серьезные изменения, достаточно лишь изменить индекс, который позволит нам преобразовать структуру строки в один из столбцов. Но как правильно это сделать, будет зависеть от каждого конкретного случая. Поэтому важно изучить, как выполняется факторизация матриц, читая книги по математике, чтобы ознакомиться с предметом.

Теперь вернемся к нашему коду, который мы рассмотрели в предыдущей теме. Для начала давайте исправим представление. Для этого просто изменим код так, как показано в приведенном ниже фрагменте.

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double  M_1[]= {
24.                        cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                        -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                    },
27.             M_2[]= {
28.                        0.0,  0.0,
29.                        1.5, -.75,
30.                        1.0,  0.0,
31.                        1.5,  .75
32.                    },
33.            M_3[M_2.Size()];

Обратите внимание, что теперь у нас больше нет индексов на массивах. Структура матриц создается так, как показано в коде, то есть, строки - это строки, а столбцы - это столбцы. Однако обратите внимание на динамические массивы, такие как M_3. Мы должны правильно определить назначаемую длину, чтобы избежать ошибок RUN-TIME при обращении к элементам этих матриц.

Это первая часть. Однако, сделав это, процедура MatrixA_x_MatrixB уже не сможет правильно выполнять вычисления. Кроме того, цикл, присутствующий в строке 42 (смотрите код в предыдущей теме), не сможет правильно расшифровать данные.

Сначала мы исправим вычисления, выполняемые в процедуре MatrixA_x_MatrixB, а потом исправим экранное построение графиков. Однако, прежде чем продолжить, отметим, что матрица M_1 практически не изменилась, так как она симметричная и квадратная. Это один из случаев, когда мы можем читать ее как в строках, так и в столбцах.

Так как большая часть кода изменится, давайте рассмотрим его новый фрагмент. Думаю, так будет проще объяснить, как всё это будет работать.

09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[], const ushort Rows, const double &B[], double &R[])
13. {
14.     uint Lines = (uint)(A.Size() / Rows);
15. 
16.     for (uint cbl = 0; cbl < B.Size(); cbl += Rows)
17.         for (uint car = 0; car < Rows; car++)
18.         {
19.             R[car + cbl] = 0;
20.             for (uint cal = 0; cal < Lines; cal++)
21.                 R[car + cbl] += (A[(cal * Rows) + car] * B[cal + cbl]);
22.         }
23. }
24. //+------------------------------------------------------------------+
25. void Plot(const int x, const int y, const double &A[])
26. {
27.     int dx[], dy[];
28. 
29.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
30.     {
31.         ArrayResize(dx, c0 + 1, A.Size());
32.         ArrayResize(dy, c0 + 1, A.Size());
33.         dx[c0] = x + (int)(A[c1++]);
34.         dy[c0] = y + (int)(A[c1++]);
35.     }
36. 
37.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
38.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
39. 
40.     ArrayFree(dx);
41.     ArrayFree(dy);
42. }
43. //+------------------------------------------------------------------+
44. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
45. {
46.     double  M_1[]={
47.                      cos(_ToRadians(angle)), sin(_ToRadians(angle)),
48.                      -sin(_ToRadians(angle)), cos(_ToRadians(angle))
49.                   },
50.             M_2[]={
51.                      0.0,  0.0,
52.                      1.5, -.75,
53.                      1.0,  0.0,
54.                      1.5,  .75
55.                   },
56.            M_3[M_2.Size()];
57.     
58.     MatrixA_x_MatrixB(M_1, 2, M_2, M_3);
59.     ZeroMemory(M_1);
60.     M_1[0] = M_1[3] = size;
61.     MatrixA_x_MatrixB(M_1, 2, M_3, M_2);
62.     Plot(x, y, M_2);
63. }
64. //+------------------------------------------------------------------+

Кажется, теперь всё стало намного сложнее, я вообще ничего не понимаю! Неужели нам нужна вся эта путаница? Не волнуйтесь, дорогие читатели. Данный код не является ни сложным, ни запутанным. На самом деле, он очень прост и понятен. Кроме того, он очень гибкий, и сейчас я объясню, почему я так считаю.

В этом фрагменте умножение между двумя матрицами происходит правильным образом. В данном случае мы реализовали модель столбец в строке, в результате чего в качестве произведения умножения получалась новая строка. Умножение происходит точно в строке 21. Я знаю, что процедура, выполняемая в строке 12, может показаться очень сложной, но это не так. Все эти переменные существуют именно для того, чтобы мы могли корректно обращаться к конкретному индексу в массиве.

Поскольку не существует тестов, гарантирующих, что количество строк в одной матрице равно количеству столбцов в другой, мы должны быть осторожны при использовании данной процедуры, чтобы избежать ошибок RUN-TIME.

Теперь, когда матрица A, которая должна организовываться в виде столбцов, умножает матрицу B, которая должна организовываться в виде строк, а результат помещается в матрицу R, построенную в виде строк, мы можем увидеть, как осуществляются вызовы. Это происходит на строках 58 и 61. Сначала давайте посмотрим на строку 58. Обратите внимание, что в качестве первой матрицы должна быть передана матрица M_1, расположенная по столбцам. В качестве второй матрицы мы должны передать матрицу M_2, которая является динамической и организована по строкам. Если мы изменим этот порядок в строке 58, то получим ошибку в вычисленных значениях. Я знаю, может показаться странным, что 2 x 3 отличается от 3 x 2, но когда речь идет о матрицах, порядок факторов действительно влияет на ее результат. Однако обратите внимание, что это похоже на то, что делалось раньше. Разумеется, второй аргумент вызова указывает на количество столбцов в первой матрице. Поскольку наша с вами цель здесь - дидактическая, я не буду проверять, можно ли умножить матрицу B (в данном случае M_2) на матрицу A (M_1). Я предполагаю, что вы не будете менять структуру, возможно, просто увеличите количество строк в матрице M_2, что и не повлияет на факторизацию в MatrixA_x_MatrixB.

Хорошо. Строки 59 и 60 уже были объяснены в предыдущей статье, а то, что происходит в строке 61, эквивалентно тому, что происходит в строке 58, поэтому мы можем считать что объяснение уже было дано. Однако в строке 62 у нас есть новый вызов, который вызывает процедуру в строке 25. Причина в том, что мы можем использовать эту процедуру в строке 25 для построения других объектов или изображений непосредственно на экране. Всё, что нам нужно сделать, это передать в эту процедуру матрицу строчного вида, где каждая строка представляет собой вершину рисуемого изображения. Данные точки, которые должны быть в матрице, должны располагаться в следующем порядке: X в первом столбце и Y во втором, поскольку мы строим график на двумерном экране. Поэтому, даже если мы рисуем что-то в 3D, нам нужно произвести вычисления в матрице, чтобы вершина в измерении Z была спроецирована на плоскость XY. Нам не нужно беспокоиться о разделении вещей или размере матрицы. Процедура Plot позаботится об этом. Обратите внимание, что в строке 27 мы объявляем два динамических массива. В строке 29 мы создаем интересный цикл for, непохожий на то, как многие привыкли его писать. В данном цикле у нас есть две переменные: одна управляется циклом, а другая - внутри кода. Переменная c0 управляется циклом, который стремится правильно создавать экземпляр индекса для dx и dy и при необходимости выделяет больше памяти. Это и делается в строках 31 и 32. Хотя это может показаться неэффективным, но посмотрите документацию по MQL5, и вы увидите, что это вовсе не так.

С другой стороны, переменная c1 управляется внутри кода. Чтобы понять это, давайте посмотрим, что происходит с c1 в строках 33 и 34. С каждой итерацией происходит увеличение на одну единицу. Однако именно c1 определяет, когда цикл for должен завершиться. Если вы не заметили, можно посмотреть в строке 29 условие завершения цикла.

Здесь мы не проверяем, правильно ли структурирован массив или матрица A. Если у нас нет двух столбцов в строке, то в какой-то момент в этом цикле for будет сгенерирована ошибка RUN-TIME, указывающая на то, что была предпринята попытка доступа к позиции, находящейся за пределами диапазона. Поэтому надо быть внимательным при создании матрицы A.

В конце всего этого мы используем строку 37 для вызова процедуры в классе CCanvas. Это делается для того, чтобы нанести фигуру матрицы на график. Линия 38 показывает, где находится точка с которой начинается рисование. Если всё пройдет успешно, мы увидим изображение ниже.

И, конечно, в строках 40 и 41 мы возвращаем операционной системе выделенную память, освобождая таким образом выделенный ресурс.

Заключительные идеи

В этих двух последних статьях, я попытался рассказать о том, что многие считают сложным или трудновыполнимым: о матричной факторизации. Я знаю, что представленный здесь материал не охватывает всех аспектов и преимуществ использования матриц в некоторых наших расчетах. Однако я хочу подчеркнуть, что очень важно понимать как разрабатывать способы вычисления матриц. Неслучайно 3D-программы, будь то игры или редакторы векторных изображений, используют именно данный вид факторизации. Даже простые на первый взгляд программы (такие как программы для работы с растровыми изображениями) также используют матричные вычисления для оптимизации работы системы.

В этих двух статьях я попытался показать это самым простым способом, поскольку я заметил, что многие новички в мире программирования, просто игнорируют необходимость учиться программировать определенные вещи. Часто они используют библиотеки или другое модное программное обеспечение, не подозревая о том, что происходит за кулисами.

Здесь я постарался максимально упростить процесс. Я сосредоточился на одной операции: умножении двух матриц. И чтобы продемонстрировать, насколько всё просто, я не стал показывать, как использовать GPU для выполнения работы, которая ведется в процедуре MatrixA_x_MatrixB, что, собственно, и происходит во многих случаях. Здесь мы используем только мощность центрального процессора. Но в целом факторизация матриц обычно выполняется не на CPU, а на GPU, с использованием OpenCL для корректного программирования.

Думаю, что в каком-то смысле я показал, что мы можем сделать гораздо больше того, что некоторые считают возможным. Изучите материал, представленный в статьях, потому что в ближайшее время я собираюсь рассказать о теме, в которой матричная факторизация является основополагающей.

И последняя деталь, которую я хочу добавить: умножение двух матриц направлено на решение конкретной задачи. Это далеко не тот метод, который традиционно изучают в книгах или в школе. Не надейтесь использовать данную модель факторизации в общем случае, потому что она не будет работать. Он подходит только для решения предложенной задачи, которая заключается во вращении объекта.