
Eigenvetores e autovalores: Análise exploratória de dados no MetaTrader 5
Introdução
A Análise de Componentes Principais (PCA) é amplamente conhecida por seu papel na redução da dimensionalidade durante a exploração de dados. No entanto, seu potencial vai muito além da redução de grandes conjuntos de dados. No centro da PCA estão os autovalores e os eigenvetores, que desempenham um papel crucial na descoberta de relações ocultas dentro dos dados. Neste artigo, exploraremos técnicas que utilizam a estrutura de autovalores para revelar essas relações ocultas.
Começaremos com a análise fatorial, demonstrando como a estrutura de autovalores ajuda a identificar variáveis latentes, oferecendo uma compreensão mais abrangente da estrutura subjacente dos dados. Ao identificar variáveis latentes, podemos expor redundâncias entre variáveis aparentemente independentes, mostrando como múltiplas variáveis podem simplesmente refletir o mesmo fator subjacente. Além disso, examinaremos como os eigenvetores e os autovalores podem ser usados para avaliar as relações entre variáveis ao longo do tempo. Ao analisar a estrutura de autovalores dos dados coletados em diferentes intervalos, podemos obter insights valiosos sobre as relações dinâmicas entre as variáveis. Isso nos permite identificar variáveis que se movem juntas ou exibem comportamentos contrastantes ao longo do tempo.
Variáveis Latentes em Dados: Análise Fatorial Principal
Análise fatorial é uma metodologia destinada a descobrir fatores ocultos que explicam as inter-relações entre as variáveis observadas nos dados. Ela representa as variáveis medidas como combinações de fatores latentes, que são construtos conhecidos por ter um efeito, mas que são difíceis de medir ou quantificar. Por exemplo, considere os indicadores que um trader usa para avaliar o comportamento do mercado. A análise fatorial poderia revelar que esses indicadores são influenciados por fatores subjacentes, como o sentimento do investidor ou a apetite ao risco. Embora seja fácil calcular indicadores técnicos, quantificar o sentimento do mercado ou o apetite ao risco é mais desafiador. É como observar ondulações na superfície de um corpo d'água turvo. As ondulações representam o que vemos, enquanto a causa subjacente permanece oculta. A análise fatorial tem como objetivo descobrir essas causas ocultas.
A análise fatorial é frequentemente confundida com uma alternativa à análise de componentes principais (PCA). Ambas as técnicas reduzem a dimensionalidade dos dados, mas diferem na forma como as variáveis reduzidas se relacionam com o conjunto original. A PCA reduz um grande conjunto de variáveis para um conjunto menor de variáveis não correlacionadas ou ortogonais, chamadas componentes principais. Esses componentes capturam a máxima variância dos dados originais. Imagine um conjunto de dados denso com centenas de variáveis. A realização de PCA pode revelar que apenas três variáveis representam mais de 99% das informações dos dados. Esses três componentes principais correspondem a propriedades distintas inerentes aos dados observados, explicadas pela combinação de partes dos dados originais. Cada componente principal é influenciado pelo conjunto denso de variáveis. Em contraste, a análise fatorial teoriza que variáveis latentes influenciam as variáveis observadas. Neste texto, focamos no cálculo dessas dimensões ocultas e nas perspectivas únicas que elas oferecem sobre as variáveis observadas, em vez de na redução da dimensionalidade.
Os autovalores e eigenvetores são conceitos matemáticos fundamentais cruciais para entender este artigo. Se a matriz A é uma matriz p por p, x é um vetor coluna de comprimento p e E é um escalar, então x é um eigenvetor de A com autovalor E se Ax=Ex. A direção do eigenvetor é significativa, não seu comprimento, e geralmente é normalizada para o comprimento unitário. Geometricamente, multiplicar um vetor por uma matriz geralmente o rotaciona, mas os eigenvetores permanecem invariáveis em direção quando multiplicados pela matriz. Essa direção é a chave para sua relevância. Em uma distribuição normal multivariada padronizada, a matriz de covariância é a matriz de correlação R. Seja V uma matriz p por m. O novo vetor aleatório y=V'x tem uma matriz de covariância C=V'RV.
A matriz V tem propriedades desejáveis que se traduzem em y. Para m=1, V é uma única coluna, e C é a variância de y. Normalizando V para que seus componentes somem a um, obtemos o eigenvetor de R correspondente ao maior autovalor. Estendendo isso para m=2, a segunda coluna de V, ortogonal à primeira, é o eigenvetor de R correspondente ao segundo maior autovalor. Esse processo continua para todas as p colunas, fazendo com que os eigenvetores de R sejam a matriz de transformação para mapear as variáveis x para variáveis independentes y que capturam a maior variância.
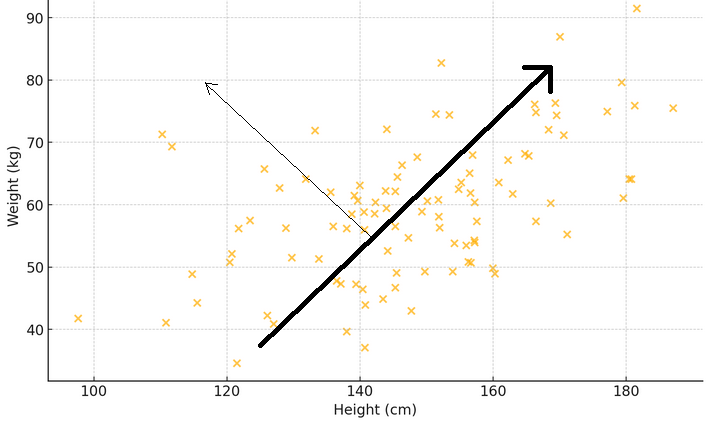
Para ilustrar o que os dois parágrafos anteriores significam, considere um gráfico de dispersão onde o eixo x mede o peso e o eixo y representa a altura de uma amostra de pessoas. Se uma linha for desenhada através dos pontos que melhor se ajusta à dispersão das medições, essa linha representará o principal padrão: pessoas mais altas tendem a ser mais pesadas. Agora, pense em um eigenvetor como uma seta que aponta para essa direção principal, mostrando a maior tendência ou o padrão dominante. O autovalor correspondente indica a força desse fenômeno. Se outra seta for desenhada perpendicular à primeira, ela mostrará um padrão secundário, como algumas pessoas podendo ser mais pesadas ou mais leves do que o esperado para sua altura.
O objetivo é determinar como cada variável observada se relaciona com os autovalores da matriz de correlação. Isso envolve calcular as correlações entre os autovalores e as variáveis observadas. Essas correlações formam uma matriz especial chamada matriz de cargas fatoriais, derivada multiplicando cada eigenvetor pela raiz quadrada de seu autovalor correspondente. Ao examinar como as variáveis se correlacionam com certos autovalores, podemos hipotetizar sobre os efeitos nas variáveis observadas. Essa análise nos ajuda a entender quais variáveis são mais relevantes para os fatores e fornece pistas sobre o número apropriado de fatores que influenciam as variáveis observadas.
Exemplo: Análise Fatorial Principal sobre Indicadores Financeiros
Nesta seção, demonstraremos a Análise Fatorial Principal (PFA) sobre um conjunto de dados de indicadores financeiros. Usaremos o MQL5 para implementar todas as etapas envolvidas no cálculo da matriz de cargas fatoriais. Começamos coletando os dados de interesse. Que, neste contexto, consistirão em alguns indicadores amostrados dentro de uma faixa específica de comprimentos de janela. Para fins de demonstração, utilizaremos dois indicadores comuns: o indicador Média Móvel (MA), que fornece informações sobre a tendência, e o Índice de Volatilidade Média (ATR), que fornece uma medida básica de volatilidade. Vários comprimentos de janela desses indicadores serão coletados ao longo de um período de tempo.
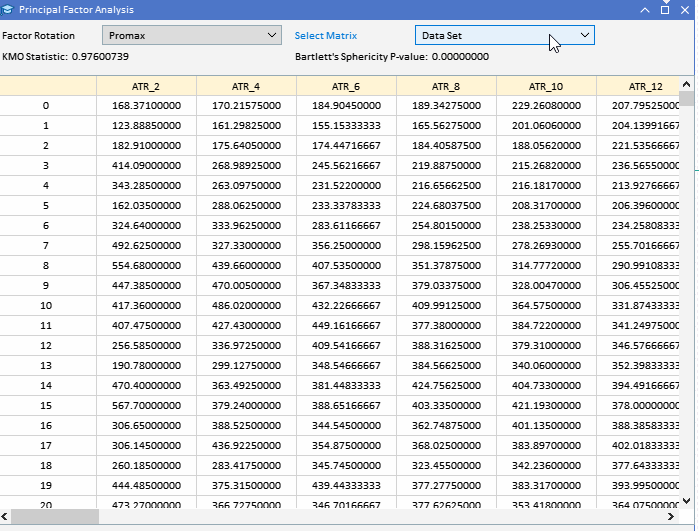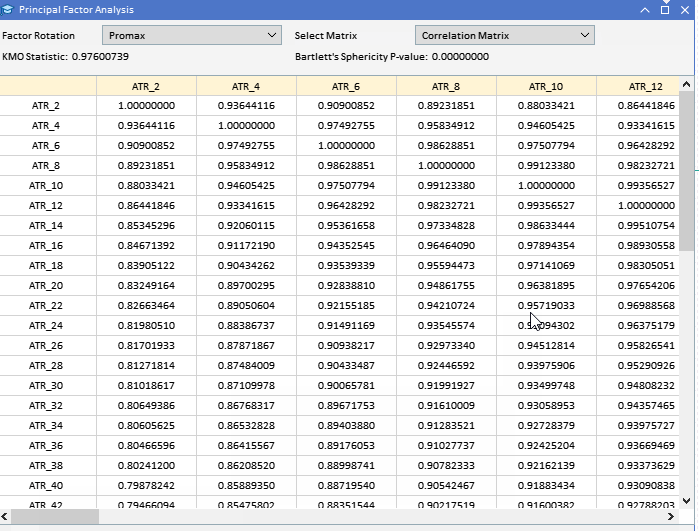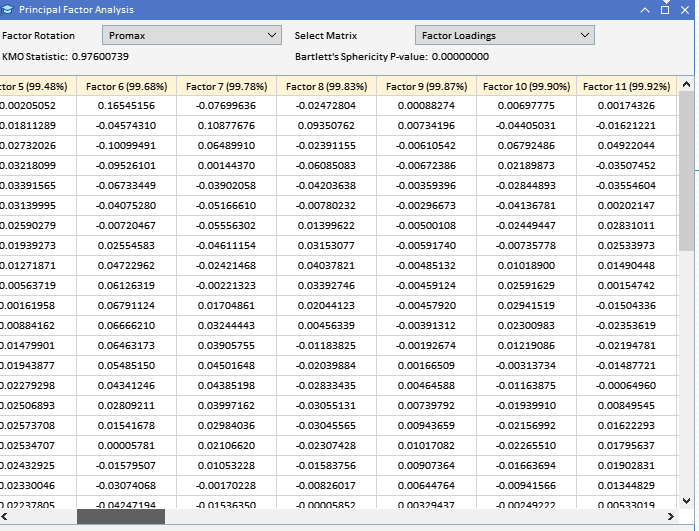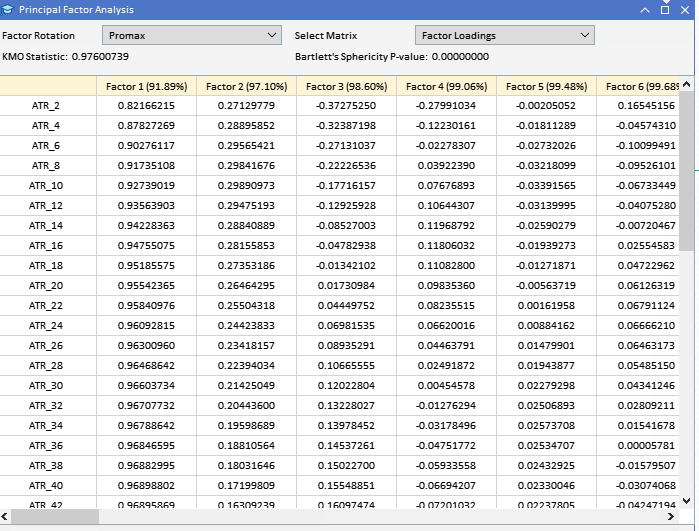
Como a maior parte da análise envolve a exame de matrizes potencialmente grandes, simplesmente imprimi-las na guia de especialistas do terminal é inadequado devido ao seu tamanho. Dado o objetivo de realizar todas as análises dentro do MetaTrader 5, sem recorrer a outras plataformas como Python ou R, foi incorporada uma interface gráfica na aplicação que implementa o PFA. Abaixo está um gráfico mostrando o conjunto de dados com o qual estaremos trabalhando neste exemplo. Cada coluna contém os valores de um indicador para um comprimento de janela particular, conforme indicado pelo cabeçalho da coluna. "ATR_2" se refere ao indicador ATR com um comprimento de janela de 2. O índice zero aponta para o valor mais antigo em tempo, no período de 2019.12.31 a 2022.12.31, com base nos preços diários do BitCoin (BTCUSD).
Antes de tentar extrair os fatores principais, seria prudente avaliar se um conjunto de dados é adequado para análise fatorial. Existem dois testes estatísticos que podem ser realizados em um conjunto de dados para determinar se as variáveis provavelmente serão explicadas por fatores latentes. O primeiro é o teste Kaiser-Meyer-Olkin (KMO). O critério KMO é uma estatística que mede a adequação dos dados da amostra para a análise fatorial. Ele quantifica o grau de correlação entre as variáveis e avalia a proporção de variância entre as variáveis que pode ser atribuída a fatores subjacentes. A medida KMO compara a magnitude dos coeficientes de correlação observados com a magnitude dos coeficientes de correlação parciais. Ela varia de 0 a 1, onde:
- Valores próximos de 1 indicam que os dados são altamente adequados para análise fatorial.
- Valores abaixo de 0.6 geralmente indicam que os dados não são adequados para análise fatorial.
Matematicamente, a estatística KMO é definida como:
Onde:
- r(ij) é o coeficiente de correlação entre as variáveis i e j.
- p(ij) é o coeficiente de correlação parcial entre as variáveis i e j.
Abaixo está uma implementação do teste KMO em MQL5. A função 'kmo()' requer três parâmetros de entrada. A matriz 'in' deve ser fornecida com o conjunto de dados das variáveis em estudo. Os resultados do teste serão enviados para o segundo e terceiro parâmetros de entrada, respectivamente. O vetor 'kmo_per_item' conterá os valores KMO para cada variável (correspondente a cada coluna da matriz 'in'), e 'kmo_total' é a estatística KMO geral para as variáveis combinadas.
//+---------------------------------------------------------------------------+ //| Calculate the Kaiser-Meyer-Olkin criterion | //| In general, a KMO < 0.6 is considered inadequate. | //+---------------------------------------------------------------------------+ void kmo(matrix &in, vector &kmo_per_item, double &kmo_total) { matrix partial_corr = partial_correlations(in); matrix x_corr = (stdmat(in)).CorrCoef(false); np::fillDiagonal(x_corr,0.0); np::fillDiagonal(partial_corr,0.0); partial_corr = pow(partial_corr,2.0); x_corr = pow(x_corr,2.0); vector partial_corr_sum = partial_corr.Sum(0); vector corr_sum = x_corr.Sum(0); kmo_per_item = corr_sum/(corr_sum+partial_corr_sum); double corr_sum_total = x_corr.Sum(); double partial_corr_sum_total = partial_corr.Sum(); kmo_total = corr_sum_total/(corr_sum_total + partial_corr_sum_total); return; }
Um teste alternativo ou adicional que pode ser realizado para avaliar um conjunto de dados é o Teste de Esfericidade de Bartlett (BTS). Ele é um teste estatístico usado para verificar se uma matriz de correlação é uma matriz identidade, o que indicaria que as variáveis são não relacionadas e inadequadas para métodos de detecção de estrutura, como a análise fatorial. Essentially, it tests if the observed correlation matrix diverges significantly from the identity matrix, where all diagonal elements are 1, indicating that variables perfectly correlate with themselves, and off-diagonal elements are 0, indicating no correlation between different variables. The test is based on the Chi-square test, whose test statistic is calculated using the following formula:
Onde:
- n é o número de observações.
- p é o número de variáveis.
-|R| é o determinante da matriz de correlação R.
A estatística do teste segue uma distribuição qui-quadrado com (p(p-1))/2 graus de liberdade. Se a estatística do teste de Bartlett for grande e o valor p associado for pequeno, tipicamente p-valor < 0.05, rejeitamos a hipótese nula. Isso sugere que a matriz de correlação difere significativamente de uma matriz identidade, indicando que as variáveis são relacionadas e adequadas para análise fatorial. Caso contrário, se o valor p for grande, não rejeitamos a hipótese nula, sugerindo que a matriz de correlação está próxima de uma matriz identidade, e as variáveis não estão significativamente correlacionadas.
O código abaixo define a função 'bartlet_sphericity()', que implementa o BTS. A função envia seus resultados para os dois últimos parâmetros de entrada. Ambos são valores escalares. 'statistic' é a estatística do qui-quadrado e 'p_value' é o valor de probabilidade computado.
//+------------------------------------------------------------------+ //| Compute the Bartlett sphericity test. | //+------------------------------------------------------------------+ void bartlet_sphericity(matrix &in, double &statistic, double &p_value) { long n,p; n = long(in.Rows()); p = long(in.Cols()); matrix x_corr = (stdmat(in)).CorrCoef(false); double corr_det = x_corr.Det(); double neg = -log(corr_det); statistic = (corr_det>0.0)?neg*(double(n)-1.0-(2.0*double(p)+5.0)/6.0):DBL_MAX; double degrees_of_freedom = double(p)*(double(p)-1.0)/2.0; int error; p_value = 1.0 - MathCumulativeDistributionChiSquare(statistic,degrees_of_freedom,error); if(error) Print(__FUNCTION__, " MathCumulativeDistributionChiSquare() error ", error); return; }
Se um ou ambos os testes fornecerem resultados encorajadores, podemos avançar com a extração dos fatores principais. Usando o conjunto de dados de indicadores, podemos ver que ambos os testes mostram que as variáveis são adequadas para a extração de fatores.
O próximo passo envolve um pequeno pré-processamento, onde o conjunto de dados é padronizado. Padronizar os dados garante que cada indicador contribua igualmente para a análise, independentemente de sua escala.
//+------------------------------------------------------------------+ //| standardize a matrix | //+------------------------------------------------------------------+ matrix stdmat(matrix &in) { vector mean = in.Mean(0); vector std = in.Std(0); std+=1e-10; matrix out = in; for(ulong row =0; row<out.Rows(); row++) if(!out.Row((in.Row(row)-mean)/std,row)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(in.Rows(), in.Cols()); } return out; }
A matriz de correlação é calculada a partir dos dados padronizados.
m_data = stdmat(in);
m_corrmat = m_data.CorrCoef(false); Em seguida, calculamos os autovalores e eigenvetores da matriz de correlação. Optamos por usar a implementação de decomposição de eigenvetores fornecida pela biblioteca Aglib devido a um problema encontrado ao usar o método "Eig()" para matrizes nativas.
CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
O problema é melhor ilustrado por meio de um exemplo. O código abaixo define um script que decompõe os eigenvetores e valores de uma matriz simétrica.
//+------------------------------------------------------------------+ //| TestEigenDecompostion.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include<Math\Alglib\linalg.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- matrix dataset = { {1,0.5,-0.2}, {0.5,1,-0.8}, {-0.2,-0.8,1} }; matrix evectors; vector evalues; dataset.Eig(evectors,evalues); Print("Eigen decomposition of \n", dataset); Print(" EVD using built in Eig() \n", evectors); Print(evalues); CMatrixDouble data(dataset); CMatrixDouble vects; CRowDouble vals; CEigenVDetect::SMatrixEVD(data,data.Rows(),1,true,vals,vects); Print(" EVD using Alglib implementation \n", vects.ToMatrix()); Print(vals.ToVector()); } //+------------------------------------------------------------------+
A saída do script é dada a seguir.
Ela mostra a diferença na forma como os eigenvetores e valores são apresentados. A implementação do Alglib ordena os vetores e valores em ordem crescente, o que é mais conveniente. O método nativo MQL5 "Eig()" não fornece nenhuma ordenação, mas este não é o principal motivo para desconsiderá-lo. Olhando para o último eigenvetor (coluna), notamos que os sinais dos valores individuais são exatamente opostos aos dos valores correspondentes gerados pelo código Alglib. Não está claro por que isso ocorre. Para confirmar se isso foi uma anomalia, a mesma decomposição foi realizada usando o Numpy do Python e os resultados do Alglib foram replicados. É óbvio que as cargas fatoriais serão sensíveis ao sinal dos valores dos membros do eigenvetor. Como as cargas fatoriais são definidas como correlações, o sinal do valor tem um significado importante.
A matriz de cargas fatoriais é derivada multiplicando cada eigenvetor pela raiz quadrada de seu autovalor correspondente.. Para evitar a possibilidade de obter números inválidos, primeiro substituímos qualquer autovalor inferior a zero por 0. Isso efetivamente descarta a dimensão associada (eigenvetor) na matriz de cargas fatoriais.
m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
Os trechos de código que vimos até agora foram extraídos da classe Cpfa, para realizar Análise Fatorial Principal (PFA) no MetaTrader 5. A classe completa é mostrada abaixo, seguida por uma tabela que documenta seus métodos públicos.
//+------------------------------------------------------------------+ //| Principal factor extraction | //+------------------------------------------------------------------+ class Cpfa { private: bool m_fitted; //flag showing if principal factors were extracted matrix m_corrmat, //correlation matrix m_data, //standardized data is here m_eigvectors, //matrix of eigen vectors of correlation matrix m_structmat; //factor loading matrix vector m_eigvalues, //vector of eigen values m_cumeigvalues; //eigen values sorted in descending order long m_indices[];//original order of column indices in input data matrix public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Cpfa(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~Cpfa(void) { } //+------------------------------------------------------------------+ //| fit() called with input matrix and extracts principal factors | //+------------------------------------------------------------------+ bool fit(matrix &in) { m_fitted = false; m_data = stdmat(in); m_corrmat = m_data.CorrCoef(false); CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_eigvectors = vects.ToMatrix(); m_eigvalues = vals.ToVector(); double sum = 0.0; double total = m_eigvalues.Sum(); if(!np::reverseVector(m_eigvalues) || !np::reverseMatrixCols(m_eigvectors)) return m_fitted; m_cumeigvalues = m_eigvalues; for(ulong i=0 ; i<m_cumeigvalues.Size() ; i++) { sum += m_eigvalues[i] ; m_cumeigvalues[i] = 100.0 * sum/total; } m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_fitted = true; return m_fitted; } //+------------------------------------------------------------------+ //| returns factor loading matrix | //+------------------------------------------------------------------+ matrix get_factor_loadings(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_structmat; } //+------------------------------------------------------------------+ //| get the eigenvector and values of correlation matrix | //+------------------------------------------------------------------+ bool get_eigen_structure(matrix &out_eigvectors, vector &out_eigvalues) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return false; } out_eigvalues = m_eigvalues; out_eigvectors = m_eigvectors; return true; } //+------------------------------------------------------------------+ //| returns variance contributions for each factor as a percent | //+------------------------------------------------------------------+ vector get_cum_var_contributions(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return vector::Zeros(1); } return m_cumeigvalues; } //+------------------------------------------------------------------+ //| get the correlation matrix of the dataset | //+------------------------------------------------------------------+ matrix get_correlation_matrix(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_corrmat; } //+------------------------------------------------------------------+ //| returns the rotated factor loadings | //+------------------------------------------------------------------+ matrix rotate_factorloadings(ENUM_FACTOR_ROTATION factor_rotation_type) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } CRotator rotator; if(!rotator.fit(m_structmat,factor_rotation_type,4,true)) return matrix::Zeros(1,1); else return rotator.get_transformed_loadings(); } };
| Método | Descrição | Tipo de Retorno |
|---|---|---|
| fit | Extrai os principais fatores da matriz de entrada in. Esta função padroniza os dados de entrada, calcula a matriz de correlação e realiza a decomposição em autovalores. Ela também calcula a matriz de carregamentos dos fatores e os autovalores cumulativos. Este é o método que deve ser chamado primeiro após a criação do objeto. | bool |
| get_factor_loadings | Retorna a matriz de carregamentos dos fatores se os principais fatores forem extraídos; caso contrário, retorna uma matriz zero. Os carregamentos serão ordenados em ordem decrescente em relação ao maior autovalor. Após a conclusão bem-sucedida de 'fit()', este e outros métodos podem ser chamados para recuperar as propriedades da análise. | matrix |
| get_eigen_structure | Retorna os autovetores e autovalores da matriz de correlação. Opcionalmente, pode ordená-los. | matrix, vector |
| get_cum_var_contributions | Retorna as contribuições cumulativas de variância de cada fator como uma porcentagem, se os principais fatores foram extraídos; caso contrário, retorna um vetor zero. | vector |
| get_correlation_matrix | Retorna a matriz de correlação do conjunto de dados se os principais fatores foram extraídos; caso contrário, retorna uma matriz zero. | matrix |
| rotate_factorloadings | Retorna a matriz de carregamentos dos fatores rotacionada usando o tipo de rotação especificado, se os principais fatores foram extraídos; caso contrário, retorna uma matriz zero. | matrix |
Agora que sabemos como obter os carregamentos dos fatores, na próxima seção veremos o que essas correlações transmitem.
Interpretando os carregamentos dos fatores
Os carregamentos dos fatores representam a correlação entre as variáveis observadas e os fatores latentes subjacentes. Eles indicam a medida em que uma variável está associada a um fator. Para facilitar a interpretação, os autovetores são organizados em ordem decrescente de acordo com a magnitude dos seus autovalores correspondentes. Isso garante que o primeiro autovetor corresponda ao maior autovalor, que se refere ao fator latente com maior influência sobre as variáveis observadas. As linhas da matriz de carregamentos dos fatores seguem a mesma ordem das colunas do conjunto de dados original, ou seja, cada linha corresponde a uma variável. As colunas representam os fatores organizados em ordem decrescente de variância explicada. Correlações acima de 0,4 ou abaixo de -0,4 são consideradas significativas. Qualquer variável com carregamentos dentro do intervalo de -0,4 a 0,4 indica que o fator correspondente tem pouco impacto sobre essa variável.
| Variáveis | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| X1 | 0.8 | 0.3 | 0.1 |
| X2 | -0.3 | -0.93 | 0.00002 |
| X3 | 0.0 | 0.342 | -1 |
| X4 | 0.5 | 0.1 | -0.38 |
| X5 | 0.5 | -0.33 | 0.44 |
Conjuntos de dados com uma estrutura simples de fatores têm variáveis que carregam fortemente em um fator e pouco nos outros. A tabela acima representa os carregamentos dos fatores de um conjunto de dados hipotético. As variáveis X1 a X4 mostram que estão carregando significativamente em fatores distintos, enquanto a variável X5 apresenta sinais mistos, pois carrega levemente em dois fatores simultaneamente. As características da variável medida, juntamente com seus carregamentos de fatores, podem fornecer pistas sobre a natureza do fator subjacente. Por exemplo, se vários indicadores econômicos carregam fortemente em um único fator, esse fator pode representar uma tendência econômica subjacente ou o sentimento do mercado. Por outro lado, se uma variável carrega moderadamente em vários fatores, isso pode sugerir que a variável é influenciada por vários fatores subjacentes, cada um contribuindo para um aspecto diferente do comportamento da variável.
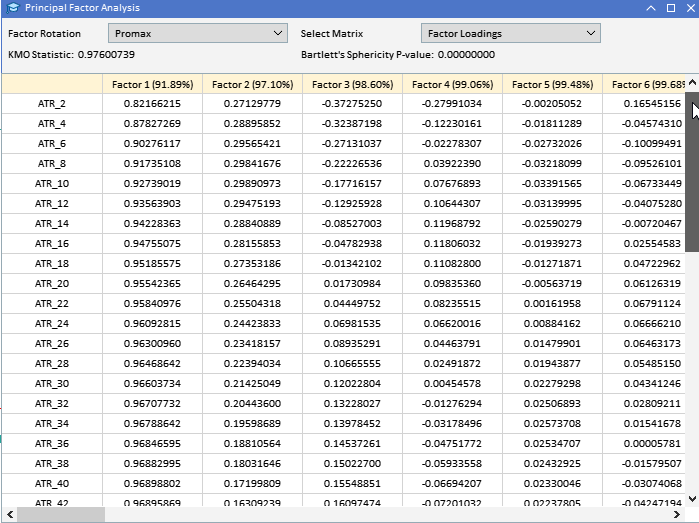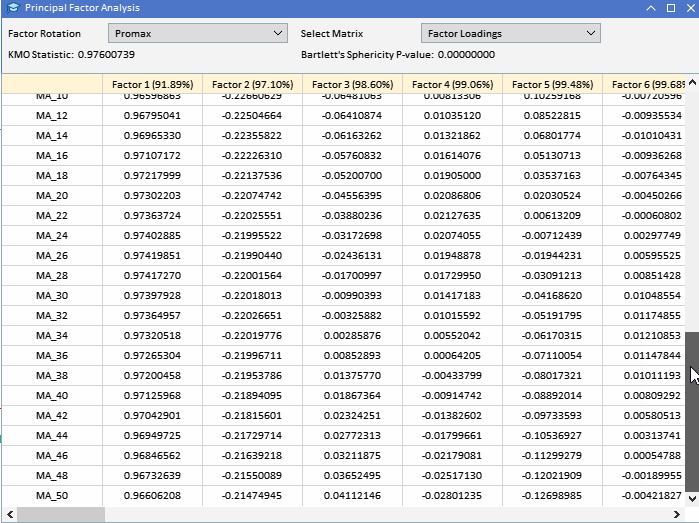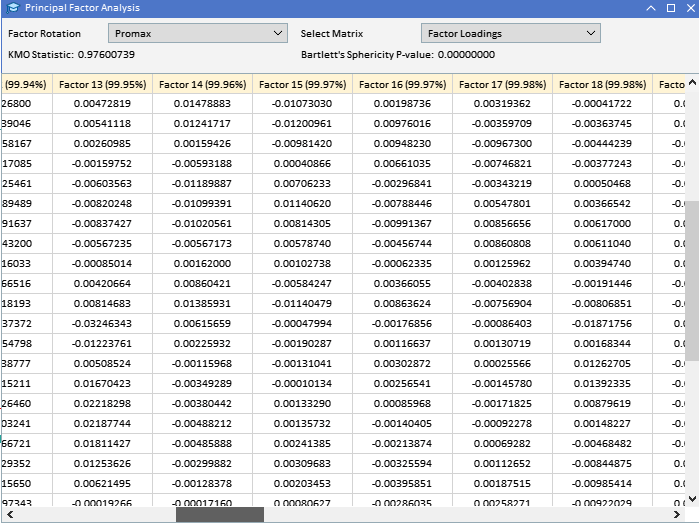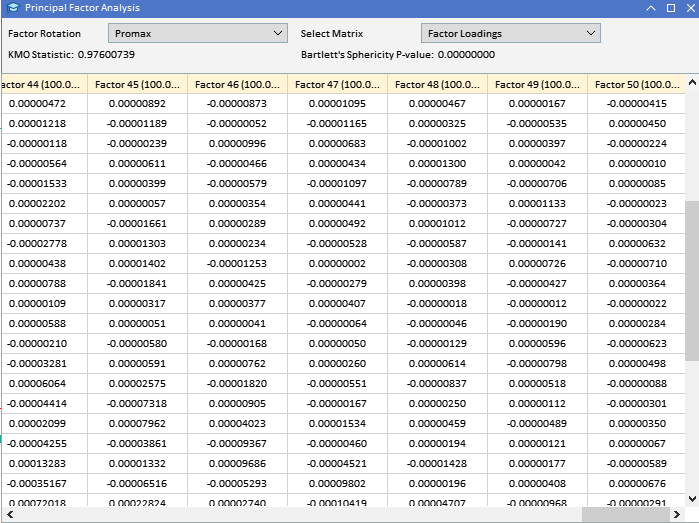
Analisando os carregamentos dos fatores das variáveis ATR coletadas anteriormente, podemos ver que a maioria das variáveis tem altos carregamentos no Fator 1, sugerindo que essas variáveis são principalmente influenciadas por este fator. O Fator 1 explica uma parte significativa da variância nessas variáveis, com a porcentagem de variância explicada indicada pelo número entre parênteses (91,89%). Embora o Fator 1 pareça dominante, algumas variáveis também têm carregamentos notáveis em outros fatores. ATR_4, ATR_6, ATR_10, ATR_14, entre outros, têm carregamentos moderados no Fator 2, indicando uma influência secundária. ATR_2, ATR_4, ATR_6, ATR_8 têm carregamentos menores, mas significativos, no Fator 3. Os Fatores 4 e além têm carregamentos menores em várias variáveis, sugerindo que eles explicam menos variância no conjunto de dados em comparação com os três primeiros fatores.
Se os carregamentos dos fatores forem difíceis de interpretar devido a uma estrutura de fatores complexa, é possível simplificar os carregamentos transformando-os para melhorar a interpretabilidade. Esse tipo de transformação é chamado de rotação de fatores. Existem dois tipos de rotações que podem ser aplicadas à matriz de carregamentos dos fatores. As rotações ortogonais mantêm a independência dos fatores. Exemplos incluem as rotações varimax e equamax. As rotações ortogonais devem ser aplicadas se os fatores forem considerados independentes. As rotações oblíquas permitem alguma dependência entre os fatores. Exemplos incluem as rotações promax e oblimin. As rotações oblíquas são apropriadas se os fatores forem suspeitos de serem inter-relacionados. Transformar as correlações por meio de rotação faz com que as correlações brutas da matriz de estrutura de fatores atinjam valores extremos (-1, 0, 1), facilitando a interpretação das correlações e amplificando os efeitos sobre as variáveis observadas.
Para facilitar as rotações, introduzimos a classe CRotator, que implementa as rotações promax e varimax.
//+------------------------------------------------------------------+ //| class implementing factor rotations | //| implements varimax and promax rotations | //+------------------------------------------------------------------+ class CRotator { private: bool m_normalize, //normalization flag m_done; //rotation flag int m_power, //exponent to which to raise the promax loadings m_maxIter; //maximum number of iterations. Used for 'varimax' double m_tol; //convergence threshold. Used for 'varimax' matrix m_loadings, //the rotated factor loadings m_rotation_mtx, //the rotation matrix m_phi; //factor correlations matrix. ENUM_FACTOR_ROTATION m_rotation_type; //rotation method employed //+------------------------------------------------------------------+ //| implements varimax rotation | //+------------------------------------------------------------------+ bool varimax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; vector norm_mat(X.Rows()); if(m_normalize) { for(ulong i = 0; i<X.Rows(); i++) norm_mat[i]=sqrt((pow(X.Row(i),2.0)).Sum()); X = X.Transpose()/np::repeat_vector_as_rows_cols(norm_mat,X.Rows()); X = X.Transpose(); } m_rotation_mtx = matrix::Eye(cols,cols); double d = 0,old_d; matrix diag,U,V,transformed,basis; vector S,ones; for(int i =0; i< m_maxIter; i++) { old_d = d; basis = X.MatMul(m_rotation_mtx); ones = vector::Ones(rows); diag.Diag(ones.MatMul(pow(basis,2.0))); transformed = X.Transpose().MatMul(pow(basis,3.0) - basis.MatMul(diag)/double(rows)); if(!transformed.SVD(U,V,S)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } m_rotation_mtx = U.Inner(V); d = S.Sum(); if(d<old_d*(1.0+m_tol)) break; } X = X.MatMul(m_rotation_mtx); if(m_normalize) { matrix xx = X.Transpose(); X = xx * np::repeat_vector_as_rows_cols(norm_mat,xx.Rows()); } else X = X.Transpose(); m_loadings = X.Transpose(); return true; } //+------------------------------------------------------------------+ //| implements promax rotation | //+------------------------------------------------------------------+ bool promax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; matrix weights,h2; h2.Init(1,1); if(m_normalize) { matrix array = X; matrix m = array.MatMul(array.Transpose()); vector dg = m.Diag(); h2.Resize(dg.Size(),1); h2.Col(dg,0); weights = array/np::repeat_vector_as_rows_cols(sqrt(dg),array.Cols(),false); } else weights = X; if(!varimax(weights)) return false; X = m_loadings; ResetLastError(); matrix Y = X * pow(MathAbs(X),double(m_power-1)); matrix coef = (((X.Transpose()).MatMul(X)).Inv()).MatMul(X.Transpose().MatMul(Y)); vector diag_inv = ((coef.Transpose()).MatMul(coef)).Inv().Diag(); if(GetLastError()) { diag_inv = ((coef.Transpose()).MatMul(coef)).PInv().Diag(); ResetLastError(); } matrix D; D.Diag(sqrt(diag_inv)); coef = coef.MatMul(D); matrix z = X.MatMul(coef); if(m_normalize) z = z * np::repeat_vector_as_rows_cols(sqrt(h2).Col(0),z.Cols(),false); m_rotation_mtx = m_rotation_mtx.MatMul(coef); matrix coef_inv = coef.Inv(); m_phi = coef_inv.MatMul(coef_inv.Transpose()); m_loadings = z; return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CRotator(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CRotator(void) { } //+------------------------------------------------------------------+ //| performs rotation on supplied factor loadings passed to /in/ | //+------------------------------------------------------------------+ bool fit(matrix &in, ENUM_FACTOR_ROTATION rot_type=MODE_VARIMX, int power = 4, bool normalize = true, int maxiter = 500, double tol = 1e-05) { m_rotation_type = rot_type; m_power = power; m_maxIter = maxiter; m_tol = tol; m_done=false; if(in.Cols()<2) { m_loadings = in; m_rotation_mtx = matrix::Zeros(in.Rows(), in.Cols()); m_phi = matrix::Zeros(in.Rows(),in.Cols()); m_done = true; return true; } switch(m_rotation_type) { case MODE_VARIMX: m_done = varimax(in); break; case MODE_PROMAX: m_done = promax(in); break; default: return m_done; } return m_done; } //+------------------------------------------------------------------+ //| get the rotated loadings | //+------------------------------------------------------------------+ matrix get_transformed_loadings(void) { if(m_done) return m_loadings; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the rotation matrix | //+------------------------------------------------------------------+ matrix get_rotation_matrix(void) { if(m_done) return m_rotation_mtx; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the factor correlation matrix | //+------------------------------------------------------------------+ matrix get_phi(void) { if(m_done && m_rotation_type==MODE_PROMAX) return m_phi; else return matrix::Zeros(1,1); } };
Aqui está uma visão geral de seus métodos públicos:
| Método | Descrição | Parâmetros: | Tipo de Retorno |
|---|---|---|---|
| fit | Executa a rotação especificada (varimax ou promax) na matriz de cargas fatoriais fornecida. | in: A matriz de cargas fatoriais a ser rotacionada | bool |
| get_transformed_loadings | Retorna a matriz de cargas fatoriais rotacionada | None | matrix |
| get_rotation_matrix | Retorna a matriz de rotação usada na transformação. | None | matrix |
| get_phi | Retorna a matriz de correlação dos fatores (somente para rotação promax). | None | matrix |
Aplicando a rotação na matriz de cargas fatoriais.
CRotator rotator; if(!rotator.fit(m_structmat,MODE_PROMAX,4,false)) return; Print(" Rotated Loadings Matrix ", rotator.get_transformed_loadings());
As cargas fatoriais rotacionadas pelo promax tornam claros os efeitos que o Fator 1 e o Fator 2 têm nas duas classes de variáveis. O Fator 1 é a principal influência sobre as variáveis MA.
O Fator 2 captura influência adicional sobre as variáveis ATR. O impacto mínimo de outros Fatores é amplificado ao capturar padrões menos significativos dentro dos dados. Esta solução rotacionada fornece uma compreensão mais clara da estrutura subjacente do conjunto de dados, facilitando uma melhor interpretação. Embora a rotação de fatores possa melhorar significativamente a interpretabilidade das cargas fatoriais, existem várias desvantagens e limitações a considerar:
- A rotação pode simplificar excessivamente a estrutura subjacente ao forçar as variáveis a se concentrarem fortemente em um único fator, o que pode ocultar inter-relações mais complexas.
- A escolha entre rotações ortogonais e oblíquas depende das suposições teóricas sobre a independência dos fatores, o que pode nem sempre ser claro ou justificado.
- Em alguns casos, a rotação pode levar a uma leve perda de variância explicada, pois o objetivo da rotação é a interpretabilidade e não maximizar a variância explicada.
- Com um grande número de variáveis e fatores, a interpretação das cargas rotacionadas ainda pode ser desafiadora, especialmente se não houver uma estrutura simples clara.
- Rotações, especialmente as iterativas como a varimax, podem ser computacionalmente caras para grandes conjuntos de dados, podendo afetar o desempenho em aplicações em tempo real.
Isso conclui nossa discussão sobre a extração principal de fatores. Em seguida, exploraremos a redundância nas variáveis com base nos fatores latentes, examinando como os fatores latentes podem revelar relações ocultas.
Redundância nas variáveis com base nos fatores latentes
Ao lidar com um grande número de variáveis, é útil identificar conjuntos de variáveis que são significativamente redundantes. Isso significa que algumas variáveis fornecem informações semelhantes, e talvez não precisemos considerar todas elas. Normalmente, a informação importante vem da própria redundância, pois pode indicar um efeito comum que impacta várias variáveis. Ao identificar grupos de variáveis altamente redundantes, podemos simplificar nossa análise, concentrando-nos em poucas variáveis representativas ou em um único fator que tenha boa correlação com o grupo.
Um método popular para identificar variáveis redundantes é usar gráficos de dispersão nos eixos principais ou rotacionados ortogonais. Variáveis que se agrupam no gráfico provavelmente são redundantes. No entanto, esse método tem suas limitações. Primeiramente, é subjetivo, e geralmente é prático lidar apenas com duas dimensões por vez para realizar uma análise eficaz. Um método intuitivo para detectar redundância envolve considerar fatores subjacentes não observáveis. Por exemplo, se tivermos três fatores (V1, V2, V3) que dão origem a variáveis observadas (X1, X2, X3), e descobrirmos que um fator (V3) é apenas ruído, então X1 e X2 podem ser redundantes quando V3 for ignorado. Em outras palavras, se X2 for apenas uma versão escalada de X1, elas são redundantes em termos dos fatores importantes (V1 e V2).
Para medir rigorosamente a redundância, consideramos as variáveis observadas como vetores em um espaço definido pelos fatores subjacentes. Quando temos variáveis observadas, podemos representá-las como vetores em um espaço multidimensional onde cada dimensão corresponde a um fator subjacente. Esses vetores mostram como cada variável se relaciona com os fatores. O ângulo entre esses vetores indica o quão semelhantes as variáveis são em termos das informações que carregam sobre os fatores subjacentes. Um ângulo menor significa que os vetores apontam quase na mesma direção, indicando alta redundância. Em outras palavras, as variáveis fornecem informações semelhantes.
Para quantificar essa redundância, podemos usar o produto escalar de vetores normalizados (vetores com comprimento 1). Esse produto escalar varia de -1 a 1, onde um produto escalar de 1 significa que os vetores são idênticos, indicando redundância perfeita. Enquanto um produto escalar de -1 significa que os vetores estão em direções opostas, o que também pode ser considerado redundante, já que saber um nos dá o oposto do outro. Um produto escalar de 0 significa que os vetores são ortogonais (independentes), indicando nenhuma redundância.
Os coeficientes para calcular as variáveis observadas a partir dos fatores subjacentes podem ser encontrados usando componentes principais. Componentes principais dominantes (com grandes autovalores) geralmente contêm a maior parte das informações úteis, enquanto componentes com autovalores pequenos costumam ser ruído. A matriz de cargas fatoriais, que mostra a correlação dos fatores com as variáveis, pode ser usada para calcular variáveis observadas padronizadas a partir dos componentes principais. Para fins práticos, geralmente tomamos o valor absoluto do produto escalar para medir a redundância, reconhecendo que vetores opostos também indicam redundância. Normalizar os vetores garante que seus comprimentos sejam 1, permitindo que o produto escalar seja uma medida direta do cosseno do ângulo entre eles.
Para calcular o grau em que duas variáveis estão relacionadas em termos de um fator oculto, geralmente precisamos primeiro determinar o número de componentes principais que consideramos importantes. Os cálculos de agrupamento se concentrarão nos dados da primeira dessas colunas da matriz de cargas fatoriais. Cada linha nessas colunas será redimensionada para que todas somem 1. O grau de semelhança entre as duas variáveis se torna o valor absoluto do produto escalar das duas linhas correspondentes da matriz de cargas fatoriais transformada.
O próximo passo é agrupar esses dados em conjuntos que constituem variáveis muito semelhantes com base em sua relação com um fator latente. Um dos melhores algoritmos de agrupamento, conhecido por produzir bons resultados, é o agrupamento hierárquico. No agrupamento hierárquico, também conhecido como agrupamento hierárquico aglomerativo (AHC), o agrupamento começa atribuindo cada variável a um grupo com um membro. Cada par possível de grupos é testado para encontrar os dois mais próximos. Esses grupos são combinados em um único grupo. Esse processo se repete até que haja apenas um grupo restante ou o grau de semelhança se torne excessivamente pequeno.
A implementação do AHC é fornecida na versão MQL5 da biblioteca Alglib. É especialmente adequada para nossos propósitos porque suporta a capacidade de implementar uma métrica de distância personalizada. Essa funcionalidade é fornecida por meio de três classes da Alglib. Para usar a implementação do agrupamento hierárquico aglomerativo da Alglib, precisamos de uma instância da estrutura CAHCReport para armazenar os resultados da operação.CAHCReport m_rep;
A classe CClusterizerState encapsula o mecanismo de clusterização. A clusterização não pode ser feita sem ela.
CClusterizerState m_cs;
O processo começa inicializando o mecanismo de clusterização, por meio de uma chamada ao método estático 'ClusterizerCreate()' da classe CClustering.
CClustering::ClusterizerCreate(m_cs);
Após a inicialização, podemos definir os parâmetros do processo de clusterização, usando outros métodos estáticos da CClustering. Todos exigem um mecanismo de clusterização inicializado.
CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);
Finalmente, 'ClusterizerRunAHC()' aciona a operação real.
CClustering::ClusterizerRunAHC(m_cs,m_rep);
Os resultados podem ser acessados através das propriedades da instância CAHCReport.
Como mencionado anteriormente, implementaremos uma métrica de distância personalizada para a operação. Isso é feito fornecendo uma matriz com distâncias iniciais para cada variável (linha nas cargas fatoriais). O trecho de código abaixo mostra como as distâncias iniciais são calculadas a partir das cargas fornecidas.
for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; }
Primeiro, normalizamos as cargas com relação ao número de dimensões consideradas.
for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } }
Essas cargas são usadas para calcular as distâncias. Além disso, as cargas normalizadas são aquelas passadas para o clusterizador. Não as cargas fatoriais brutas. Todo o código que implementa o agrupamento está contido na classe CCluster.
//+------------------------------------------------------------------+ //| cluster a set of points | //+------------------------------------------------------------------+ class CCluster { private: CClusterizerState m_cs; CAHCReport m_rep; matrix m_pd[]; //+------------------------------------------------------------------+ //| Preprocesses input matrix before clusterization | //+------------------------------------------------------------------+ bool customDist(matrix &structure, ulong num_factors, matrix& out[], bool calculate_custom_distances = true) { int nvars; double dotprod, length; nvars = int(structure.Rows()); int ndim = (num_factors && num_factors<=structure.Cols())?int(num_factors):int(structure.Cols()); if(out.Size()<2) if(out.Size()<2 && (ArrayResize(out,2)!=2 || !out[0].Resize(nvars,ndim) || !out[1].Resize(nvars,nvars))) { Print(__FUNCTION__, " error ", GetLastError()); return false; } if(calculate_custom_distances) { for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; } out[1].Fill(0.0); for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } } } else { out[0] = np::sliceMatrixCols(structure,0,ndim); } return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CCluster(void) { CClustering::ClusterizerCreate(m_cs); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CCluster(void) { } //+------------------------------------------------------------------+ //| cluster a set | //+------------------------------------------------------------------+ bool cluster(matrix &in_points, ulong factors=0, ENUM_LINK_METHOD linkage=MODE_COMPLETE, ENUM_DIST_CRIT dist = DIST_CUSTOM) { if(!customDist(in_points,factors,m_pd,dist==DIST_CUSTOM)) return false; CMatrixDouble pp(m_pd[0]); CMatrixDouble pd(m_pd[1]); CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); if(dist==DIST_CUSTOM) CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage); CClustering::ClusterizerRunAHC(m_cs,m_rep); return m_rep.m_terminationtype==1; } //+------------------------------------------------------------------+ //| output clusters to vector array | //+------------------------------------------------------------------+ bool get_clusters(vector &out[]) { if(m_rep.m_terminationtype!=1) { Print(__FUNCTION__, " no cluster information available"); return false; } if(ArrayResize(out,m_rep.m_pz.Rows())!=m_rep.m_pz.Rows()) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int i = 0; i<m_rep.m_pm.Rows(); i++) { int zz = 0; for(int j = 0; j<m_rep.m_pm.Cols()-2; j+=2) { int from = m_rep.m_pm.Get(i,j); int to = m_rep.m_pm.Get(i,j+1); if(!out[i].Resize((to-from)+zz+1)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int k = from; k<=to; k++,zz++) out[i][zz] = m_rep.m_p[k]; } } return true; } };
A função 'cluster()' realiza o agrupamento hierárquico em um conjunto dado de pontos de entrada. Ela recebe quatro parâmetros: uma referência para uma matriz de pontos de entrada, o número de fatores a considerar, o método de agrupamento a ser usado e o critério de distância. Primeiro, calcula uma matriz de distâncias personalizada se o critério de distância especificado for personalizado. Se o cálculo da distância falhar, a função retorna falso. Em seguida, inicializa duas matrizes, pp e pd, a partir dos dados de distância calculados. A função então define os pontos para o agrupamento usando o critério de distância, com o padrão sendo a Euclidiana se o critério não for configurado para a opção personalizada. Se o critério de distância for personalizado, define as distâncias para o agrupamento de acordo.Após configurar a distância e os pontos, a função configura o algoritmo de agrupamento hierárquico com o método de agrupamento especificado. Ela executa o algoritmo de agrupamento hierárquico aglomerativo e verifica o tipo de término do processo de agrupamento. A função retorna verdadeiro se o tipo de término for 1, indicando sucesso no agrupamento, caso contrário, retorna falso.
A função 'get_clusters()' extrai e exibe os clusters dos resultados de um processo de agrupamento hierárquico. Ela recebe um parâmetro: um array de vetores out[], que será preenchido com os clusters. A função primeiro verifica se o tipo de término do processo de agrupamento é 1, indicando sucesso no agrupamento. Caso contrário, imprime uma mensagem de erro e retorna falso. Em seguida, a função itera por cada linha da matriz m_rep.m_pm, que contém as informações do agrupamento. Para cada linha, inicializa uma variável zz para rastrear o índice no vetor de saída. Ela então itera pelas colunas da linha atual, processando pares de colunas (representando os índices de início e fim dos clusters). Para cada par, calcula o intervalo de índices (de from a to) e redimensiona o vetor de saída atual para acomodar os elementos do cluster. Se o redimensionamento falhar, imprime uma mensagem de erro e retorna falso. Finalmente, a função preenche o vetor de saída atual com os elementos do cluster, iterando de from a to e incrementando zz para cada elemento. Se o processo for concluído com sucesso, a função retorna verdadeiro, indicando que os clusters foram extraídos e armazenados com sucesso no array out.
O trecho de código abaixo mostra como usar a classe CCluster.
vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); }O MetaTrader 5 não possui ferramentas para visualizar diretamente os resultados do Agrupamento Hierárquico Aglomerativo (AHC). Embora o console do terminal possa exibir alguns resultados, não é amigável para visualizar resultados complexos como os do AHC. Os resultados do AHC são melhor visualizados através de dendrogramas, que mostram a estrutura hierárquica dos agrupamentos de dados. Um dendrograma ilustra como os clusters são formados pela união de pontos de dados ou clusters passo a passo. Abaixo está um dendrograma desenhado manualmente que mostra os agrupamentos do nosso conjunto de dados de indicadores.
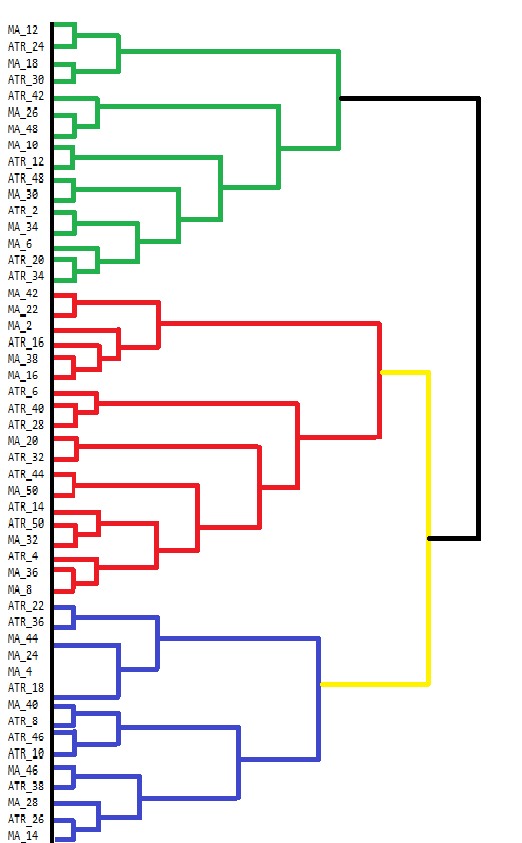
O dendrograma mostra clusters de variáveis que são mais semelhantes entre si. Variáveis que se unem em níveis mais baixos (mais próximos da parte inferior do dendrograma) são mais semelhantes entre si do que aquelas que se unem mais acima. Por exemplo, MA_12 e MA_24 são mais semelhantes entre si comparadas com ATR_18. O dendrograma usa diferentes cores para indicar diferentes clusters. Os clusters em verde, vermelho, azul e amarelo destacam grupos de variáveis que estão fortemente relacionadas. Cada cor representa um conjunto de variáveis que exibem alta semelhança ou redundância.
A altura em que dois clusters se unem fornece uma indicação da dissimilaridade entre eles. Quanto menor a altura, mais semelhantes são os clusters. Clusters que se unem em níveis mais altos, como o preto na parte superior, indicam maiores diferenças entre esses clusters. Esse agrupamento hierárquico pode informar decisões sobre a seleção de variáveis. Ao analisar os clusters, pode-se decidir focar em certas variáveis representativas dentro de cada cluster para uma análise mais aprofundada, simplificando assim o conjunto de dados sem perder informações significativas.
O código MQL5 usado para coletar e analisar o conjunto de dados de indicadores está contido no script EDA.mq5. Ele utiliza todas as ferramentas de código descritas no artigo, que são definidas em pfa.mqh.
//+------------------------------------------------------------------+ //| EDA.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\Slope.ex5" #resource "\\Indicators\\CMMA.ex5" #include<pfa.mqh> #include<ErrorDescription.mqh> #property script_show_inputs //+------------------------------------------------------------------+ //|indicator type | //+------------------------------------------------------------------+ enum SELECT_INDICATOR { CMMA=0,//CMMA SLOPE//SLOPE }; //--- input parameters input uint period_inc=2;//lookback increment input uint max_lookback=50; input ENUM_MA_METHOD AppliedMA = MODE_SMA; input datetime SampleStartDate=D'2019.12.31'; input datetime SampleStopDate=D'2022.12.31'; input string SetSymbol="BTCUSD"; input ENUM_TIMEFRAMES SetTF = PERIOD_D1; input ENUM_FACTOR_ROTATION AppliedFactorRotation = MODE_PROMAX; input ENUM_DIST_CRIT AppliedDistanceCriterion = DIST_CUSTOM; input ENUM_LINK_METHOD AppliedClusterAlgorithm = MODE_COMPLETE; input ulong Num_Dimensions = 10; //---- string csv_header=""; //csv file header int size_sample, //training set size size_observations, //size of of both training and testing sets combined maxperiod, //maximum lookback indicator_handle=INVALID_HANDLE; //long moving average indicator handle //--- vector indicator[]; //indicator indicator values; //--- matrix feature_matrix; //full matrix of features; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //---get relative shift of sample set int samplestart,samplestop,num_features; samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate); samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate); num_features = int((max_lookback/period_inc)*2); //---check for errors from ibarshift calls if(samplestart<0 || samplestop<0) { Print(ErrorDescription(GetLastError())); return; } //---set the size of the sample sets size_observations=(samplestart - samplestop) + 1 ; maxperiod=int(max_lookback); //---check for input errors if(size_observations<=0 || maxperiod<=0) { Print("Invalid inputs "); return; } //---allocate memory if(ArrayResize(indicator,num_features)<num_features) { Print(ErrorDescription(GetLastError())); return; } //----get the full collection of indicator values int period_len; int k=0; //--- for(SELECT_INDICATOR select_indicator = 0; select_indicator<2; select_indicator++) { for(int iperiod=0; iperiod<int(indicator.Size()/2); iperiod++) { period_len=int((iperiod+1) * period_inc); int try=10; while(try) { switch(select_indicator) { case CMMA: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\CMMA.ex5",AppliedMA,period_len); break; case SLOPE: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\Slope.ex5",period_len); break; } if(indicator_handle==INVALID_HANDLE) try--; else break; } if(indicator_handle==INVALID_HANDLE) { Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError()); return; } Comment("copying data to buffer for indicator ",period_len); try = 0; while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try<10) { try++; Sleep(5000); } if(try<10) ++k; else { Print("error copying to indicator buffers ",GetLastError()); Comment(""); return; } if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle)) indicator_handle=INVALID_HANDLE; } } //---resize matrix if(!feature_matrix.Resize(size_observations,indicator.Size())) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //---copy collected data to matrix for(ulong i = 0; i<feature_matrix.Cols(); i++) if(!feature_matrix.Col(indicator[i],i)) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //--- Comment(""); //---test dataset for principal factor analysis suitability //---kmo test vector kmo_vect; double kmo_stat; kmo(feature_matrix,kmo_vect,kmo_stat); Print("KMO test statistic ", kmo_stat); //---Bartlett sphericity test double bs_stat,bs_pvalue; bartlet_sphericity(feature_matrix,bs_stat,bs_pvalue); Print("Bartlett sphericity test p_value ", bs_pvalue); //---Extract the principal factors Cpfa fa; //--- if(!fa.fit(feature_matrix)) return; //--- matrix fld = fa.get_factor_loadings(); //--- matrix rotated_fld = fa.rotate_factorloadings(AppliedFactorRotation); //--- Print(" factor loading matrix ", fld); //--- Print("\n rotated factor loading matrix ", rotated_fld); //--- matrix egvcts; vector egvals; fa.get_eigen_structure(egvcts,egvals,false); Print("\n vects ", egvcts); Print("\n evals ", egvals); //--- vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); } } //+------------------------------------------------------------------+
Coerência em Séries Temporais
Ao analisar variáveis ao longo do tempo, suas relações podem mudar inesperadamente. Variáveis normalmente relacionadas podem de repente se desviar, sinalizando um possível problema. Por exemplo, mudanças na temperatura podem impactar a demanda de eletricidade, o que então afeta os preços do gás natural. Se seu padrão usual mudar, isso pode indicar que algo incomum está acontecendo. Da mesma forma, variáveis que normalmente se comportam de forma independente podem começar a se mover juntas, como quando diferentes setores do mercado de ações sobem simultaneamente devido a boas notícias econômicas.
Medir a coerência envolve quantificar quão relacionadas estão um conjunto de variáveis de séries temporais dentro de uma janela de tempo móvel. Um método básico é verificar quanto da variância é capturada pelo maior autovalor. No entanto, esse método pode ser limitante, pois considera apenas uma dimensão. Uma abordagem mais abrangente envolve somar os maiores autovalores, particularmente quando existem várias relações entre as variáveis. Essa abordagem fornece uma visão mais precisa da coerência geral em um sistema com inter-relações complexas, mas requer saber de antemão quais são os fatores mais relevantes. Algo que pode não ser possível ou simplesmente ser subjetivo demais.
Uma abordagem mais geral é necessária para cenários em que o número de relações é desconhecido ou flutua ao longo do tempo, especialmente com um grande número de variáveis. Em cenários com dimensionalidade desconhecida, podemos visualizar os autovalores ordenados do maior para o menor, como membros de uma orquestra. A chave para produzir uma música bonita é regular os diferentes instrumentos de maneira uniforme. Se os membros da orquestra não conseguirem seguir em união no nível correto, a música resultante será terrível. A coesão será ruim. Imagine o som produzido por cada membro da orquestra como um valor ponderado contribuindo para a música que o público ouve. O desequilíbrio nesses valores representa a coerência. Calculamos uma soma ponderada, com os pesos representando o volume que cada instrumento pode produzir.
Se cada instrumento (variável) estiver tocando sua própria melodia de forma independente, o som geral será desorganizado e caótico, representando zero de coerência. No entanto, quando os instrumentos estão perfeitamente sincronizados, tocando em harmonia, eles produzem uma peça musical coesa e bonita, representando plena coerência. A coerência, nessa analogia, é como a harmonia da orquestra, indicando quão bem os instrumentos (variáveis) estão tocando juntos. Se a harmonia mudar repentinamente, sugere que algo incomum está acontecendo com os instrumentos ou a composição.
Considere dois extremos. Se as variáveis forem completamente independentes. A matriz de correlação dessas variáveis será uma matriz identidade, e todos os autovalores serão iguais (1.0). A soma ponderada (devido aos pesos simétricos) será zero, refletindo zero de coerência. Alternativamente, se houver correlação perfeita entre as variáveis, apenas um autovalor não zero existirá, igual ao número de variáveis. A soma ponderada se torna o número de variáveis, que após normalização (dividido pelo número de variáveis) resulta em uma coerência de 1.0, refletindo a correlação perfeita.Este método oferece uma medida de coerência de 0-1 baseada no desequilíbrio na distribuição dos autovalores, sem fazer suposições sobre dimensionalidade.
Para ilustrar a coerência, produziremos um indicador que mede a coerência dos preços de fechamento de diferentes símbolos dentro de uma janela de tempo. Este indicador será chamado Coherence.mq5. Os usuários poderão medir a coesão entre vários símbolos, adicionando-os como uma lista separada por vírgulas de nomes de instrumentos. O indicador emprega uma abordagem diferente para calcular as correlações entre várias variáveis. Desta vez, usamos o coeficiente de correlação não paramétrico de Spearman.
covar[0][0] = 1.0 ; for(int i=1 ; i<npred ; i++) { for(int j=0 ; j<i ; j++) { for(int k=0 ; k<lookback ; k++) { nonpar1[k] = iClose(stringbuffer[i],PERIOD_CURRENT,ibar+k); nonpar2[k] = iClose(stringbuffer[j],PERIOD_CURRENT,ibar+k); } if(!MathCorrelationSpearman(nonpar1,nonpar2,covar[i][j])) Print(" MathCorrelationSpearman failed ", GetLastError(), " :", ibar); } covar[i][i] = 1.0 ; }
Como estamos usando a implementação de EVD da Aglib, não precisamos definir a matriz completa de correlações, apenas precisamos construir o triângulo superior ou inferior. Não precisamos dos autovetores, apenas dos autovalores.
CMatrixDouble cdata(covar); if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Rows(),0,false,evals,evects)) { Print(" EVD failed ", GetLastError(), " :", ibar); coherenceBuffer[ibar]=0.0; continue; }
Para obter a distribuição dos autovalores na orientação correta, temos que inverter o vetor.
vector eval = evals.ToVector(); if(!np::reverseVector(eval)) Print(" failed vecter reversal operation : ", ibar);
A coesão é calculada usando os autovalores.
double center = 0.5 * (npred - 1) ; double sum = 0.0; for(ulong i=0 ; i<eval.Size() ; i++) { sum += (center - i) * eval[i] / center ; } coherenceBuffer[ibar] = sum / eval.Sum();
O código completo está anexado no final do artigo. Vamos ver como o indicador se comporta com diferentes comprimentos de janela, medindo a coerência entre as criptomoedas BTCUSD, DOGUSD e XRPUSD.
Ao observar o gráfico de 60 dias da Coerência, ele conseguiu dissipar as preconcepções pessoais de que esses símbolos se movem com coerência notável. O que surpreende é o quanto isso flutua. Com valores variando por todo o espectro de valores possíveis.
À medida que avançamos para janelas de tempo maiores, começamos a ver períodos de estabilidade na coerência, mas novamente, a natureza dessa coerência é inesperada. Existem períodos significativos em que há quase zero de coerência.
Conclusão
O uso de autovalores e autovetores nessas técnicas avançadas ressalta sua versatilidade e importância fundamental na ciência de dados. Eles fornecem uma estrutura robusta para redução de dimensionalidade, reconhecimento de padrões e descoberta de estruturas latentes em conjuntos de dados complexos. Ao ir além da PCA, desbloqueamos um conjunto mais rico de ferramentas que oferecem percepções mais detalhadas. Este texto demonstra que autovetores e autovalores são muito mais do que abstrações matemáticas; são as pedras angulares de técnicas analíticas sofisticadas que os traders modernos podem usar para obter uma vantagem. Todo o código demonstrado no artigo está anexado no arquivo compactado. A tabela abaixo lista os arquivos disponíveis para download.| Arquivo | Descrição |
|---|---|
| Mql5\Include\np.mqh | Arquivo de inclusão que contém várias utilitárias de funções de matrizes e vetores. |
| Mql5\Include\pfa.mqh | pfa.mqh fornece a definição das classes Cpfa, CCluster e CRotator. Bem como a definição da função para as implementações dos testes KMO e BTS. |
| Mql5\Scripts\EDA.mq5 | O script demonstra o uso de todas as ferramentas de código descritas no artigo, coletando um conjunto de dados de indicadores personalizados para Análise de Fatores Principais. |
| Mql5\Scripts\TestEigenDecomposition.mq5 | Este script reproduz os problemas mencionados, com relação ao método de matriz 'Eig()' embutido. |
| Mql5\Indicators\Coherence.mq5 | Este é o indicador de Coerência aplicado a 3 símbolos. |
| Mql5\Experts\PrincipalFactors.mq5 | Este é o código-fonte da aplicação referenciada para visualização de grandes matrizes. O código depende da venerável biblioteca Easy and Fast GUI, que pode ser encontrada na base de código MQL5. |
| Mql5\Experts\PrincipalFactors.ex5 | Esta é uma versão compilada da listagem acima. |
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/15229
 Como Integrar o Conceito de Smart Money (BOS) Junto com o Indicador RSI em um EA
Como Integrar o Conceito de Smart Money (BOS) Junto com o Indicador RSI em um EA
 Criando um Limitador de Drawdown Diário EA em MQL5
Criando um Limitador de Drawdown Diário EA em MQL5
 Criando uma Interface Gráfica de Usuário Interativa em MQL5 (Parte 2): Adicionando Controles e Responsividade
Criando uma Interface Gráfica de Usuário Interativa em MQL5 (Parte 2): Adicionando Controles e Responsividade
 Do básico ao intermediário: Definições (II)
Do básico ao intermediário: Definições (II)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso