
固有ベクトルと固有値:MetaTrader 5での探索的データ分析
はじめに
主成分分析(PCA)は、データ探索における次元削減の役割で広く知られています。しかし、その可能性は大規模なデータセットを削減するだけにとどまりません。PCAの中核にあるのは固有値と固有ベクトルであり、これらはデータ内に潜む関係性を解明するための重要な手段です。この記事では、固有構造を活用してこうした隠れた関係を明らかにするテクニックを探ります。
まず因子分析から始め、固有構造がどのように潜在変数の同定に役立つかを示し、データの基礎構造のより包括的な理解を提供します。潜在変数を特定することで、一見独立した変数間の冗長性を明らかにし、複数の変数が単に同じ根本的な要因を反映している可能性を示すことができます。さらに、固有ベクトルと固有値をどのように使用すれば、経時的な変数間の関係を評価できるかを検討します。異なる間隔で収集されたデータの固有構造を分析することで、変数間の動的関係について貴重な洞察を得ることができます。これにより、時間の経過とともに連動したり、対照的な挙動を示したりする変数を特定することができます。
データの潜在変数:主因子分析
因子分析は、データ中の観測変数間の相互関係を説明する隠れた要因を発見するための方法論です。これは、測定された変数を潜在因子の組み合わせとして表し、効果があることが知られているが測定や定量化が困難な構成要素を意味します。例えば、トレーダーが市場の動きを評価するために使用する指標を考えてみましょう。要因分析により、これらの指標は投資家の感情やリスク選好度といった基礎的要因の影響を受けていることが明らかになる可能性があります。テクニカル指標を計算するのは簡単かもしれませんが、市場の感情やリスク選好度を定量化するのはより難しくなります。濁った水面の波紋を観察するようなものです。波紋は目に見えるものを表しているが、根本的な原因は隠されています。因子分析は、こうした隠れた原因を明らかにすることを目的としています。
因子分析は、しばしば主成分分析(PCA)の代替と誤解されます。どちらの手法もデータの次元を減らしますが、削減された変数が元の集合にどのように関係するかという点で異なります。PCAは、大きな変数の集合を、主成分と呼ばれる相関のない、あるいは直交する変数の小さな集合に還元します。これらの成分は、元のデータの最大分散をキャプチャします。何百もの変数を持つ高密度のデータセットを想像してください。PCAを実施すると、たった3つの変数がデータの情報の99%以上を表していることがわかるかもしれません。これらの3つの主成分は、元のデータのビットを組み合わせることによって説明される、観測データに固有の明確な特性に対応しています。各主成分は、密な変数セットの影響を受けます。これに対して因子分析では、潜在変数が観測変数に影響を与えると理論化します。このテキストでは、次元削減よりもむしろ、これらの隠れた次元の計算と、それらが観測された変数に与えるユニークな視点に焦点を当てます。
固有値と固有ベクトルは、この記事を理解する上で極めて重要な数学の基本概念です。行列Aをp×p行列、xを長さpの列ベクトル、Eをスカラーとすると、Ax=Exのとき、xは固有値Eを持つAの固有ベクトルです。固有ベクトルは長さではなく方向が重要で、通常は単位長さに正規化されます。幾何学的に言えば、通常ベクトルに行列を掛けるとベクトルの方向が変わりますが、固有ベクトルの場合、その方向は変わりません。この不変性こそが、固有ベクトルの重要な特性なのです。標準化された多変量正規分布において、共分散行列は相関行列Rです。Vをp×mの行列とします。新しいランダムベクトルy=V'xは共分散行列C=V'RVを持ちます。
行列Vは、yに変換される望ましい性質を持っています。m=1の場合、Vは1列で、Cはyの分散です。Vを正規化してその成分の和が1になるようにすると、最大の固有値に対応するRの固有ベクトルが得られます。これをm=2に拡張すると、Vの2列目は1列目と直交し、2番目に大きな固有値に対応するRの固有ベクトルとなります。このプロセスをすべてのp列について続け、Rの固有ベクトルを、x変数を最も分散を捕捉する独立y変数にマッピングするための変換行列にします。
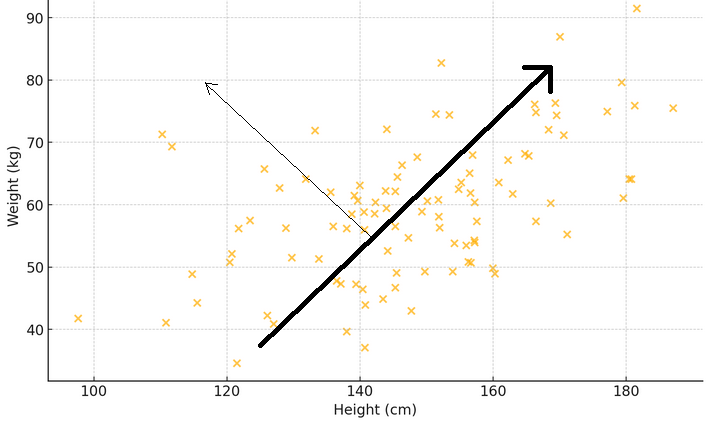
前述の2つの段落を具体的に説明するために、X軸が体重、Y軸が身長を示す散布図を考えてみましょう。測定値の広がりに最も一致する点を線で結ぶと、この線が主なパターンを表します。つまり、背の高い人の方が体重が重い傾向があります。ここで、固有ベクトルをこの主要な方向を指し示す矢印と考えてください。これは、データの中で最も顕著なトレンドや支配的なパターンを示します。対応する固有値は、このパターンの強さを表しています。最初の矢印に垂直な方向に別の矢印を引くと、例えば身長に対して体重が相対的に重い人や軽い人がいることを示すような、二次的なパターンが見えてきます。
目的は、各観測変数が相関行列の固有値とどのように関係しているかを明らかにすることです。これは、固有値と観測された変数の間の相関を計算することを含みます。これらの相関は,各固有ベクトルに対応する固有値の平方根を掛けることで得られ、因子負荷行列と呼ばれる特別な行列を形成します。変数が特定の固有値とどのように相関するかを調べることで、観測された変数への影響について仮説を立てることができます。この分析は、どの変数が要因に最も関連しているかを理解するのに役立ち、観察された変数に影響を与える要因の適切な数についての手がかりを提供します。
例:金融指標の主因子分析
このセクションでは、金融指標のデータセットについて主因子分析(PFA)を実証します。MQL5を使用して、因子負荷行列の計算に関わるすべてのステップを実装します。まず、関心のあるデータを集めることから始めます。この文脈では、指定された窓の長さの範囲内でサンプリングされたいくつかの指標で構成されます。ここでは、トレンドに関する情報を提供する移動平均(MA)指標と、ボラティリティの基本的な指標を提供する平均トゥルーレンジ(Average True Range: ATR)の2つの一般的な指標を使用します。これらの指標は、一定期間にわたっていくつかの期間の長さを収集します。
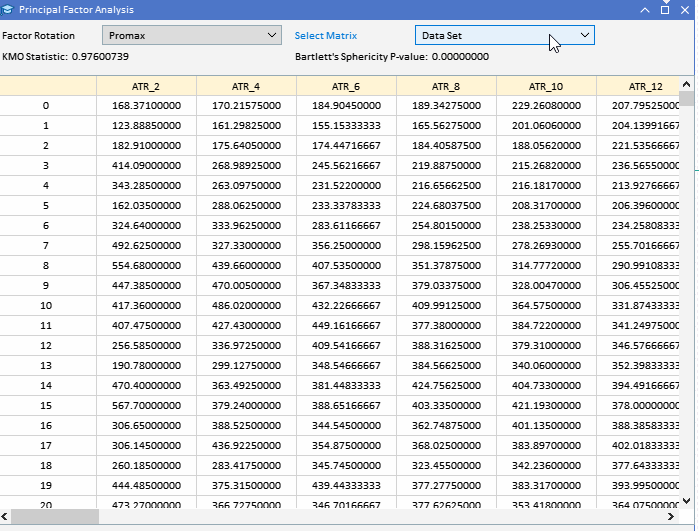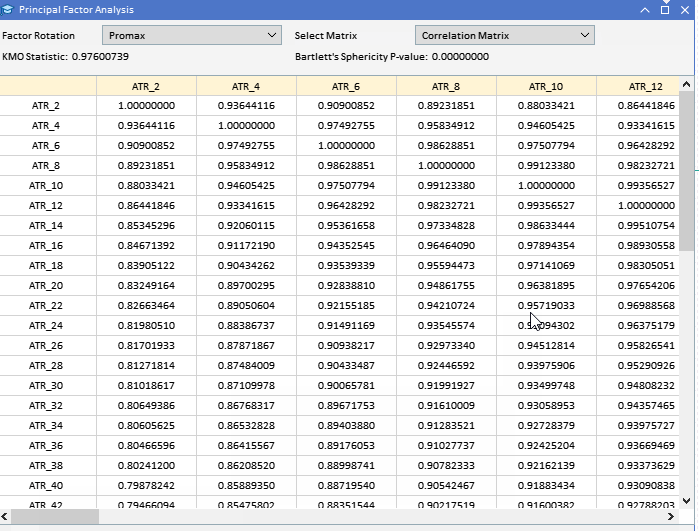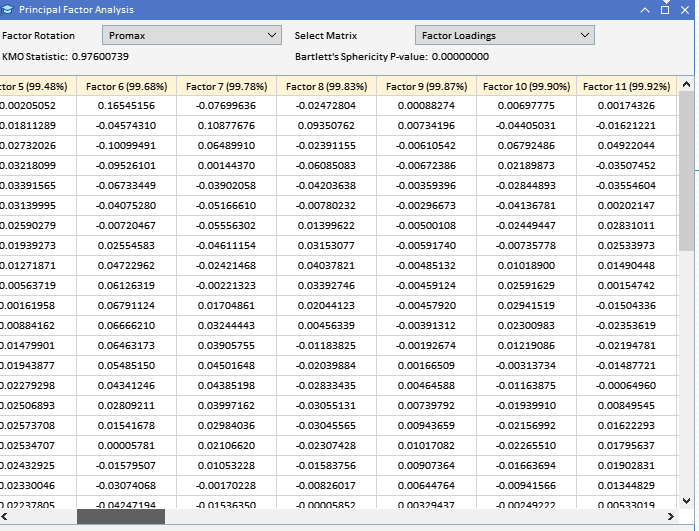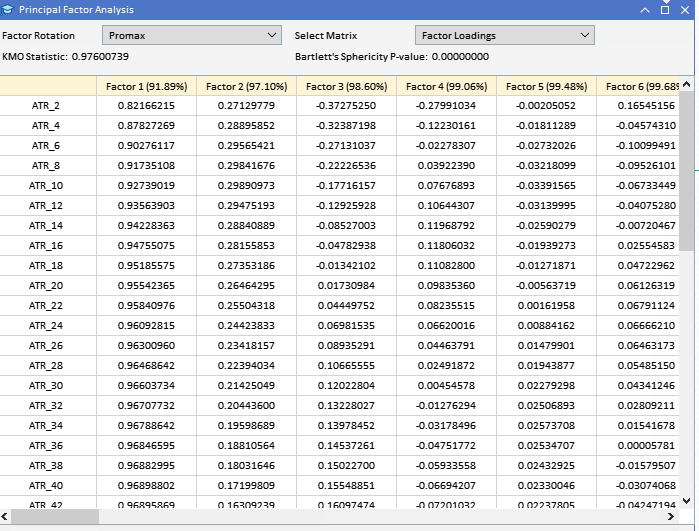
ほとんどの分析では、潜在的に大きな行列を調べる必要があるため、単純に端末の[エキスパート]タブに印刷するだけでは、その大きさのために不十分です。PythonやRのような他のプラットフォームに切り替えることなく、すべての分析をMetaTrader 5内で実行するという目的を考慮し、PFAを実装するアプリケーションにグラフィカルユーザーインターフェイスを組み込みます。 以下は、この例で扱うデータセットを示す図です。各列には、列のヘッダーで指定された特定のウィンドウの長さに対する指標の値が含まれます。「ATR_2」は、窓の長さが2のATR指標を指します。ゼロ指数は、ビットコイン(BTCUSD)の日次価格に基づく2019.12.31から2022.12.31の期間で、時間的に最も古い値を指します。
主因子の抽出を試みる前に、データセットが因子分析に適しているかどうかを評価することが賢明でしょう。変数が潜在因子によって説明される可能性が高いかどうかを明らかにするために、データ集合でおこなうことができる2つの統計的検定があります。1つ目は、KMO (Kaiser-Meyer-Olkin)検定です。KMO基準は、因子分析のためのサンプルデータの妥当性を測定する統計量です。これは変数間の相関の程度を定量化し、共通分散である可能性のある変数間の分散の割合、つまり根本的な要因に帰することができる割合を評価します。KMO尺度は、観察された相関係数の大きさを偏相関係数の大きさと比較します。範囲は0から1までです。
- 1に近い値は、データが因子分析に非常に適していることを示します。
- 一般的に0.6以下の値は、データが因子分析に適していないことを示します。
数学的には、KMO統計量は次のように定義されます。
ここで
- r(ij):変数iとjの相関係数
- p(ij):変数iとjの間の偏相関係数
以下は、KMOテストのMQL5による実装です。関数kmo()は3つの入力パラメータを必要とします。行列inには、研究対象の変数のデータセットを指定します。 テストの結果は、それぞれ2番目と3番目の入力パラメータに出力されます。ベクトルkmo_per_itemは,各変数(in行列の各列に対応する)のKMO値を含み、 kmo_totalは,組み合わされた変数の全体的なKMO 統計量です。
//+---------------------------------------------------------------------------+ //| Calculate the Kaiser-Meyer-Olkin criterion | //| In general, a KMO < 0.6 is considered inadequate. | //+---------------------------------------------------------------------------+ void kmo(matrix &in, vector &kmo_per_item, double &kmo_total) { matrix partial_corr = partial_correlations(in); matrix x_corr = (stdmat(in)).CorrCoef(false); np::fillDiagonal(x_corr,0.0); np::fillDiagonal(partial_corr,0.0); partial_corr = pow(partial_corr,2.0); x_corr = pow(x_corr,2.0); vector partial_corr_sum = partial_corr.Sum(0); vector corr_sum = x_corr.Sum(0); kmo_per_item = corr_sum/(corr_sum+partial_corr_sum); double corr_sum_total = x_corr.Sum(); double partial_corr_sum_total = partial_corr.Sum(); kmo_total = corr_sum_total/(corr_sum_total + partial_corr_sum_total); return; }
データセットを評価するためにおこなうことができる別のテストは、 バートレットの球性検定(BTS)です。 これは、相関行列が恒等行列であるかどうかを調べるために使用される統計的検定であり、変数が無関係であることを示し、因子分析などの構造検出法には適しません。本質的に、これは観察された相関行列が、すべての対角要素が1であり、変数がそれ自身と完全に相関していることを示し、非対角要素が0であり、異なる変数間に相関がないことを示す恒等行列から有意に発散しているかどうかを検定します。 検定はカイ二乗検定に基づいており、その検定統計量は以下の式で計算されます。
ここで
- nは観測の数
- pは変数の数
- |R|は相関行列Rの行列式
検定統計量は、自由度(p(p-1))/2のカイ2乗分布に従います。 バートレットの検定統計量が大きく、関連するp値が小さい場合(典型的にはp値<0.05)、帰無仮説を棄却します。このことは、相関行列が恒等行列と有意に異なることを示唆しており、変数が関連し、因子分析に適していることを示しています。そうでない場合、p値が大きければ帰無仮説を棄却できず、相関行列は恒等行列に近く、変数は有意に相関していないことを示唆します。
以下のコードは、BTSを実装するbartlet_sphericity()関数を定義しています。この関数は、その結果を最後の2つの入力パラメータに出力します。どちらもスカラー値です。statisticはカイ二乗統計量、p_valueは計算された確率値です。
//+------------------------------------------------------------------+ //| Compute the Bartlett sphericity test. | //+------------------------------------------------------------------+ void bartlet_sphericity(matrix &in, double &statistic, double &p_value) { long n,p; n = long(in.Rows()); p = long(in.Cols()); matrix x_corr = (stdmat(in)).CorrCoef(false); double corr_det = x_corr.Det(); double neg = -log(corr_det); statistic = (corr_det>0.0)?neg*(double(n)-1.0-(2.0*double(p)+5.0)/6.0):DBL_MAX; double degrees_of_freedom = double(p)*(double(p)-1.0)/2.0; int error; p_value = 1.0 - MathCumulativeDistributionChiSquare(statistic,degrees_of_freedom,error); if(error) Print(__FUNCTION__, " MathCumulativeDistributionChiSquare() error ", error); return; }
どちらか、あるいは両方のテストで有望な結果が得られれば、主因子抽出に進むことができます。指標のデータセットを用いると、両テストとも変数が因子抽出に適していることがわかります。
次のステップでは、データセットを標準化する前処理を少しおこないます。データを標準化することで、各指標がその規模に関係なく、平等に分析に寄与するようになります。
//+------------------------------------------------------------------+ //| standardize a matrix | //+------------------------------------------------------------------+ matrix stdmat(matrix &in) { vector mean = in.Mean(0); vector std = in.Std(0); std+=1e-10; matrix out = in; for(ulong row =0; row<out.Rows(); row++) if(!out.Row((in.Row(row)-mean)/std,row)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(in.Rows(), in.Cols()); } return out; }
相関行列は標準化されたデータから計算されます。
m_data = stdmat(in);
m_corrmat = m_data.CorrCoef(false); 次に相関行列の固有値と固有ベクトルを計算します。ネイティブ行列に対してEig()メソッドを使用する際に問題が発生したため、Aglibライブラリが提供する固有ベクトル分解実装を使用することにしました。
CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
この問題は、例を挙げて説明するのが一番わかりやすいです。以下のコードでは、対称行列の固有ベクトルと値を分解するスクリプトを定義しています。
//+------------------------------------------------------------------+ //| TestEigenDecompostion.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include<Math\Alglib\linalg.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- matrix dataset = { {1,0.5,-0.2}, {0.5,1,-0.8}, {-0.2,-0.8,1} }; matrix evectors; vector evalues; dataset.Eig(evectors,evalues); Print("Eigen decomposition of \n", dataset); Print(" EVD using built in Eig() \n", evectors); Print(evalues); CMatrixDouble data(dataset); CMatrixDouble vects; CRowDouble vals; CEigenVDetect::SMatrixEVD(data,data.Rows(),1,true,vals,vects); Print(" EVD using Alglib implementation \n", vects.ToMatrix()); Print(vals.ToVector()); } //+------------------------------------------------------------------+
スクリプトの出力を次に示します。
これは、固有ベクトルと値の表示方法の違いを示しています。Alglibの実装では、ベクトルと値を昇順に並び替えるので、より便利です。MQL5のネイティブメソッドEig()は順序付けを提供しませんが、これはこれを中傷する主な理由ではありません。最後の固有ベクトル(列)を見ると、個々の値の符号がAlglibコードから出力された対応する値の符号と正反対であることに気づきます。その理由は定かではありません。これが異常かどうかを確認するために、PythonのNumpyを使用して同じデコンポストを実行し、Alglibの結果を再現しました。 因子負荷量が固有ベクトルのメンバー値の符号に敏感であることは明らかです。負荷量は相関関係として定義されるため、値の符号は重要な意味を持ちます。
因子負荷行列は、各固有ベクトルに対応する固有値の平方根を乗じることで導かれます。無効な数値が得られる可能性を防ぐため、まず0未満の固有値を0に置き換えます。これは、因子負荷行列の関連する次元(固有ベクトル)を効果的に破棄します。
m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
これまで見てきたコードスニペットは、MetaTrader 5で主因子法(Principal Factor Analysis: PFA)を実施するためのCpfaクラスから抽出したものです。クラス全体を以下に示し、publicメソッドを表で説明します。
//+------------------------------------------------------------------+ //| Principal factor extraction | //+------------------------------------------------------------------+ class Cpfa { private: bool m_fitted; //flag showing if principal factors were extracted matrix m_corrmat, //correlation matrix m_data, //standardized data is here m_eigvectors, //matrix of eigen vectors of correlation matrix m_structmat; //factor loading matrix vector m_eigvalues, //vector of eigen values m_cumeigvalues; //eigen values sorted in descending order long m_indices[];//original order of column indices in input data matrix public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Cpfa(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~Cpfa(void) { } //+------------------------------------------------------------------+ //| fit() called with input matrix and extracts principal factors | //+------------------------------------------------------------------+ bool fit(matrix &in) { m_fitted = false; m_data = stdmat(in); m_corrmat = m_data.CorrCoef(false); CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_eigvectors = vects.ToMatrix(); m_eigvalues = vals.ToVector(); double sum = 0.0; double total = m_eigvalues.Sum(); if(!np::reverseVector(m_eigvalues) || !np::reverseMatrixCols(m_eigvectors)) return m_fitted; m_cumeigvalues = m_eigvalues; for(ulong i=0 ; i<m_cumeigvalues.Size() ; i++) { sum += m_eigvalues[i] ; m_cumeigvalues[i] = 100.0 * sum/total; } m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_fitted = true; return m_fitted; } //+------------------------------------------------------------------+ //| returns factor loading matrix | //+------------------------------------------------------------------+ matrix get_factor_loadings(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_structmat; } //+------------------------------------------------------------------+ //| get the eigenvector and values of correlation matrix | //+------------------------------------------------------------------+ bool get_eigen_structure(matrix &out_eigvectors, vector &out_eigvalues) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return false; } out_eigvalues = m_eigvalues; out_eigvectors = m_eigvectors; return true; } //+------------------------------------------------------------------+ //| returns variance contributions for each factor as a percent | //+------------------------------------------------------------------+ vector get_cum_var_contributions(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return vector::Zeros(1); } return m_cumeigvalues; } //+------------------------------------------------------------------+ //| get the correlation matrix of the dataset | //+------------------------------------------------------------------+ matrix get_correlation_matrix(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_corrmat; } //+------------------------------------------------------------------+ //| returns the rotated factor loadings | //+------------------------------------------------------------------+ matrix rotate_factorloadings(ENUM_FACTOR_ROTATION factor_rotation_type) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } CRotator rotator; if(!rotator.fit(m_structmat,factor_rotation_type,4,true)) return matrix::Zeros(1,1); else return rotator.get_transformed_loadings(); } };
| メソッド | 詳細 | リターンタイプ |
|---|---|---|
| fit | 入力行列inから主因子を抽出します。この関数は入力データを標準化し、相関行列を計算し、固有分解をおこないます。また、因子負荷行列と累積固有値を計算します。これは、オブジェクトのインスタンス化後に最初に呼ばれるべきメソッドです。 | bool |
| get_factor_loadings | 主因子が抽出された場合は因子負荷行列を返し、そうでない場合は 0 の行列を返します。負荷量は、最大の固有値を基準に降順に並び替えられます。fit()」が正常に終了すると、このメソッドや他のメソッドを呼び出して、解析のプロパティを取得できます。 | matrix |
| get_eigen_structure | 相関行列の固有ベクトルおよび固有値を返します。オプションで並び替えます。 | matrix、 vector |
| get_cum_var_contributions | 主因子が抽出された場合、各因子の累積分散寄与をパーセンテージとして返します。それ以外の場合は、ゼロベクトルを返します。 | vector |
| get_correlation_matrix | 主因子が抽出された場合はデータセットの相関行列を返し,そうでない場合は0の行列を返します。 | matrix |
| rotate_factorloadings | 主因子が抽出された場合、指定された回転タイプを使用して回転された因子負荷量行列を返します。そうでない場合は0の行列を返します。 | matrix |
因子負荷量の求め方はわかったので、次のセクションでは、これらの相関が何を示しているかを見てみましょう。
因子負荷量の解釈
因子負荷量は、観測された変数と潜在的な因子との間の相関を示しています。これにより、各変数がどの程度その因子と関連しているかが分かります。解釈を容易にするため、固有ベクトルは対応する固有値の大きさに基づいて降順に並べられています。これは、最初の固有ベクトルが最大の固有値に対応し、観測された変数に最も高い影響力を持つ潜在因子を参照することを保証します。因子負荷行列の行は、元のデータセットの列に対応しており、各行がそれぞれの変数に対応しています。列は、説明された分散の降順に並べられた因子を示しています。因子負荷量が0.4以上または-0.4以下の相関は有意とみなされます。負荷量が-0.4~0.4の範囲にある変数は、対応する因子がその変数にほとんど影響しないことを示します。
| 変数 | 因子1 | 因子2 | 因子3 |
|---|---|---|---|
| X1 | 0.8 | 0.3 | 0.1 |
| X2 | -0.3 | -0.93 | 0.00002 |
| X3 | 0.0 | 0.342 | -1 |
| X4 | 0.5 | 0.1 | -0.38 |
| X5 | 0.5 | -0.33 | 0.44 |
単純な因子構造を持つデータセットでは、特定の因子への負荷が高く、他の因子への負荷が低い変数が見られます。 上の表は、仮想的なデータセットの因子負荷量を表しています。変数X1からX4は、それらが別個の因子に有意にローディングしていることを示す一方、変数X5は、同時に2つの因子にマイルドにローディングしているため、複雑なシグナルを与えています。 因子負荷量と結びついた変数の特性は、潜在的な因子の性質に関する手がかりを提供します。 例えば、複数の経済指標が1つの要因に高い負荷をかけている場合、この要因は根本的な経済トレンドや市場心理を表している可能性があります。逆に、ある変数が複数の要因に中程度の負荷をかけている場合は、その変数がいくつかの基本的な要因の影響を受けていて、それぞれがその変数の行動の異なる側面に寄与していることを示唆している可能性があります。
先に収集したATR変数の因子負荷量を見ると、ほとんどの変数が第1因子の負荷量が高く、これらの変数が主にこの因子の影響を受けていることが示唆されます。第1因子は、これらの変数の分散のかなりの部分を説明し、その割合は括弧内の数字で示されています(91.89%)。第1因子が支配的に見えますが、いくつかの変数は他の因子にも顕著な負荷量を持ちます。ATR_4、ATR_6、ATR_10、ATR_14などは、第2因子の負荷量が中程度であり、二次的な影響を示しています。ATR_2、ATR_4、ATR_6、ATR_8は、第3因子への負荷量は小さいが有意です。第4因子とそれ以降の因子は、さまざまな変数にわたって負荷量が小さくなっており、最初の3因子と比較して、データセットの分散をより少なく占めていることを示唆しています。
複雑な因子構造によって因子負荷量の解釈が困難な場合、因子回転という手法を使って負荷量を変換し、解釈を単純化することができます。このような変換は因子回転と呼ばれます。因子負荷量行列に適用できる回転には2種類あります。直交回転は因子の独立性を維持し、バリマックス回転やエクアマックス回転がその例です。因子が独立していると考えられる場合には、直交回転が適しています。一方、斜め回転は因子間の依存性をある程度許容し、プロマックス回転やオブリミン回転がその例です。要因の相互関係が疑われる場合は、斜め回転が適切です。回転によって相関を変換すると、因子構造行列の生の相関が極値(-1,0,1)になり、相関の解釈が容易になり、観察された変数への効果が増幅されます。
回転を容易にするために、プロマックス回転とバリマックス回転を実装するCRotatorクラスを紹介します。
//+------------------------------------------------------------------+ //| class implementing factor rotations | //| implements varimax and promax rotations | //+------------------------------------------------------------------+ class CRotator { private: bool m_normalize, //normalization flag m_done; //rotation flag int m_power, //exponent to which to raise the promax loadings m_maxIter; //maximum number of iterations. Used for 'varimax' double m_tol; //convergence threshold. Used for 'varimax' matrix m_loadings, //the rotated factor loadings m_rotation_mtx, //the rotation matrix m_phi; //factor correlations matrix. ENUM_FACTOR_ROTATION m_rotation_type; //rotation method employed //+------------------------------------------------------------------+ //| implements varimax rotation | //+------------------------------------------------------------------+ bool varimax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; vector norm_mat(X.Rows()); if(m_normalize) { for(ulong i = 0; i<X.Rows(); i++) norm_mat[i]=sqrt((pow(X.Row(i),2.0)).Sum()); X = X.Transpose()/np::repeat_vector_as_rows_cols(norm_mat,X.Rows()); X = X.Transpose(); } m_rotation_mtx = matrix::Eye(cols,cols); double d = 0,old_d; matrix diag,U,V,transformed,basis; vector S,ones; for(int i =0; i< m_maxIter; i++) { old_d = d; basis = X.MatMul(m_rotation_mtx); ones = vector::Ones(rows); diag.Diag(ones.MatMul(pow(basis,2.0))); transformed = X.Transpose().MatMul(pow(basis,3.0) - basis.MatMul(diag)/double(rows)); if(!transformed.SVD(U,V,S)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } m_rotation_mtx = U.Inner(V); d = S.Sum(); if(d<old_d*(1.0+m_tol)) break; } X = X.MatMul(m_rotation_mtx); if(m_normalize) { matrix xx = X.Transpose(); X = xx * np::repeat_vector_as_rows_cols(norm_mat,xx.Rows()); } else X = X.Transpose(); m_loadings = X.Transpose(); return true; } //+------------------------------------------------------------------+ //| implements promax rotation | //+------------------------------------------------------------------+ bool promax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; matrix weights,h2; h2.Init(1,1); if(m_normalize) { matrix array = X; matrix m = array.MatMul(array.Transpose()); vector dg = m.Diag(); h2.Resize(dg.Size(),1); h2.Col(dg,0); weights = array/np::repeat_vector_as_rows_cols(sqrt(dg),array.Cols(),false); } else weights = X; if(!varimax(weights)) return false; X = m_loadings; ResetLastError(); matrix Y = X * pow(MathAbs(X),double(m_power-1)); matrix coef = (((X.Transpose()).MatMul(X)).Inv()).MatMul(X.Transpose().MatMul(Y)); vector diag_inv = ((coef.Transpose()).MatMul(coef)).Inv().Diag(); if(GetLastError()) { diag_inv = ((coef.Transpose()).MatMul(coef)).PInv().Diag(); ResetLastError(); } matrix D; D.Diag(sqrt(diag_inv)); coef = coef.MatMul(D); matrix z = X.MatMul(coef); if(m_normalize) z = z * np::repeat_vector_as_rows_cols(sqrt(h2).Col(0),z.Cols(),false); m_rotation_mtx = m_rotation_mtx.MatMul(coef); matrix coef_inv = coef.Inv(); m_phi = coef_inv.MatMul(coef_inv.Transpose()); m_loadings = z; return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CRotator(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CRotator(void) { } //+------------------------------------------------------------------+ //| performs rotation on supplied factor loadings passed to /in/ | //+------------------------------------------------------------------+ bool fit(matrix &in, ENUM_FACTOR_ROTATION rot_type=MODE_VARIMX, int power = 4, bool normalize = true, int maxiter = 500, double tol = 1e-05) { m_rotation_type = rot_type; m_power = power; m_maxIter = maxiter; m_tol = tol; m_done=false; if(in.Cols()<2) { m_loadings = in; m_rotation_mtx = matrix::Zeros(in.Rows(), in.Cols()); m_phi = matrix::Zeros(in.Rows(),in.Cols()); m_done = true; return true; } switch(m_rotation_type) { case MODE_VARIMX: m_done = varimax(in); break; case MODE_PROMAX: m_done = promax(in); break; default: return m_done; } return m_done; } //+------------------------------------------------------------------+ //| get the rotated loadings | //+------------------------------------------------------------------+ matrix get_transformed_loadings(void) { if(m_done) return m_loadings; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the rotation matrix | //+------------------------------------------------------------------+ matrix get_rotation_matrix(void) { if(m_done) return m_rotation_mtx; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the factor correlation matrix | //+------------------------------------------------------------------+ matrix get_phi(void) { if(m_done && m_rotation_type==MODE_PROMAX) return m_phi; else return matrix::Zeros(1,1); } };
publicメソッドの概要は以下の通りです。
| メソッド | 詳細 | パラメータ | 戻り値の型 |
|---|---|---|---|
| fit | 指定された因子負荷量行列に対して,指定された回転(バリマックスまたはプロマックス)をおこないます | in:回転される因子負荷量行列 | bool |
| get_transformed_loadings | 回転された因子負荷量行列を返します | なし | matrix |
| get_rotation_matrix | 変換に使用した回転行列を返します | なし | matrix |
| get_phi | 因子相関行列を返します(プロマックス回転の場合のみ) | なし | matrix |
因子負荷量行列に回転を適用します。
CRotator rotator; if(!rotator.fit(m_structmat,MODE_PROMAX,4,false)) return; Print(" Rotated Loadings Matrix ", rotator.get_transformed_loadings());
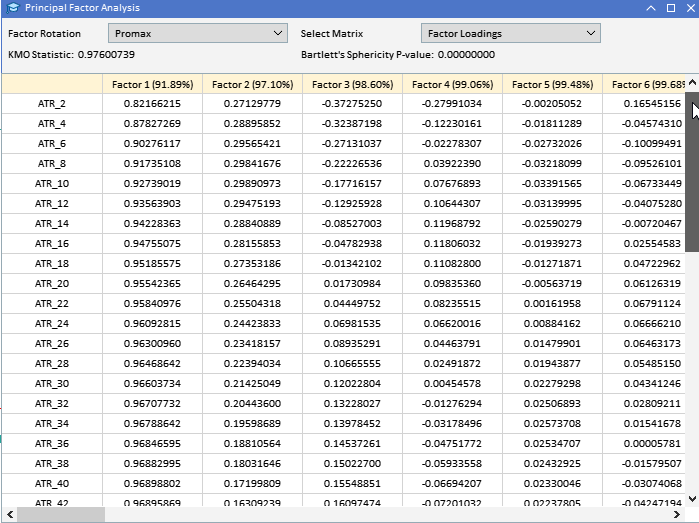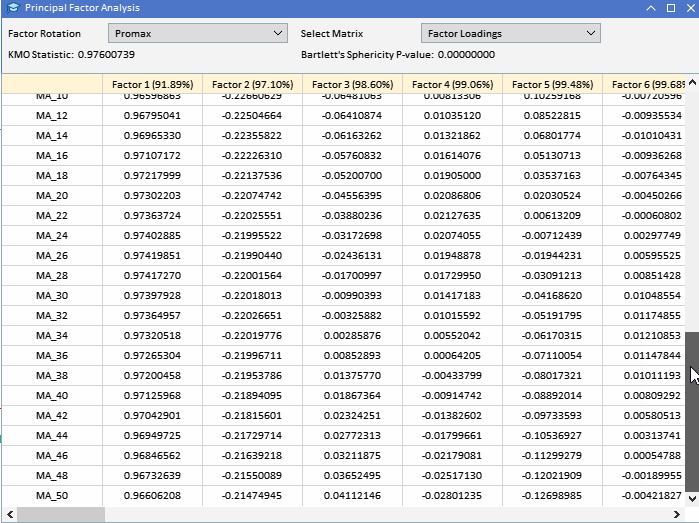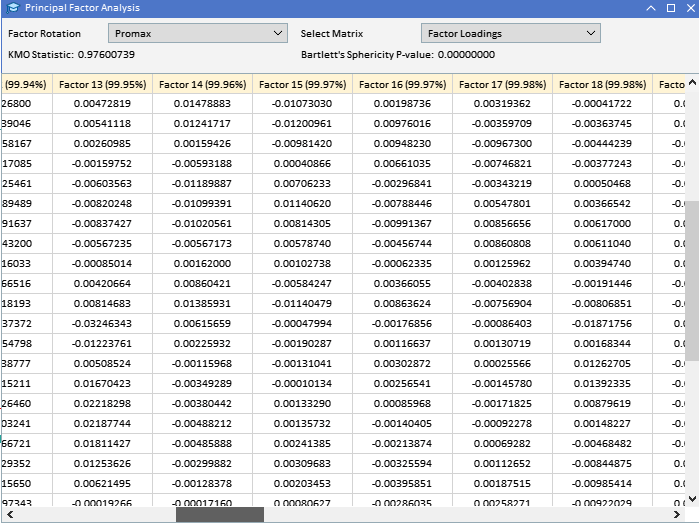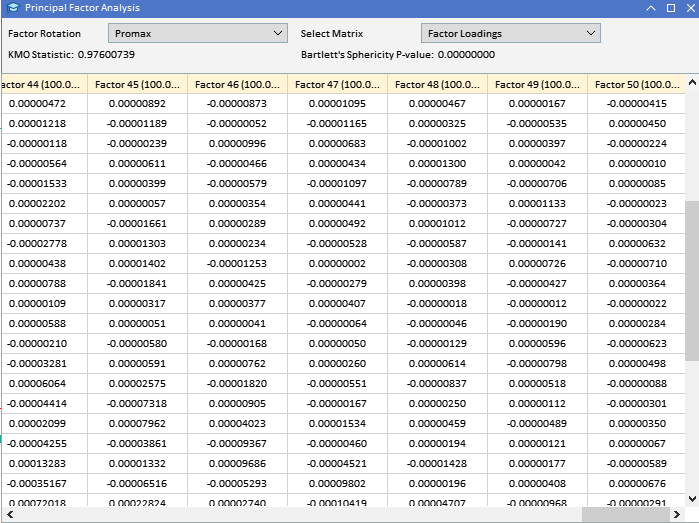
プロマックス回転した因子負荷量は、第1因子と第2因子が2つのクラスの変数に及ぼす影響を明確にしています。第1因子は、MA変数に支配的な影響を及ぼしています。
第2因子は、ATR変数へのさらなる影響を捉えます。データ内のあまり重要でないパターンを捉えることで、他の因子が与える影響は最小限に抑えられます。この回転解法は、データセットの基本構造をより明確に理解し、より良い解釈を容易にします。因子回転は、因子負荷量の解釈可能性を大いに高めることができるが、考慮すべきいくつかの欠点と限界があります。
- 回転は、変数を単一の因子に高負荷させることで根本的な構造を単純化しすぎる可能性があり、より複雑な相互関係を覆い隠してしまう可能性があります。
- 直交回転と斜交回転のどちらを選択するかは、因子の独立性に関する理論的仮定に依存しますが、これは必ずしも明確で正当化されるとは限りません。
- 回転の目的は説明分散の最大化よりも解釈可能性であるため、場合によっては回転によって説明分散がわずかに失われることがあります。
- 変数と因子の数が多く、単純な構造が明確でない場合、回転後の負荷量の解釈は依然として難しいことがあります。
- 回転、特にバリマックスのような反復的な回転は、大規模なデータセットでは計算コストがかかり、リアルタイムアプリケーションのパフォーマンスに影響を与える可能性があります。
これで、主因子抽出に関する議論は終わりです。次に、潜在因子に基づく変数の冗長性を探り、潜在因子がどのように隠れた関係を明らかにするかを検証します。
潜在因子に基づく変数の冗長性
多くの変数を扱う際に、冗長な変数セットを特定することは非常に有用です。冗長な変数とは、類似した情報を提供する変数群を指し、すべてを考慮する必要はないかもしれません。冗長性は、変数間に共通する影響を示し、重要な情報を明らかにする可能性があります。冗長性の高い変数のグループを識別することで、いくつかの代表的な変数またはグループとよく相関する単一の要因に焦点を当てることで、分析を単純化することができます。
冗長な変数を見つける一般的な方法の一つに、主軸または回転直交軸を用いた散布図があります。散布図上で密集している変数は、冗長である可能性が高いです。しかし、この方法には限界があります。まず、主観的な判断が必要であり、通常、一度に2次元しか分析できません。冗長性を検出する直感的な方法は、観測不可能な基礎的要因を考慮することです。例えば、観測変数(X1、X2、X3)を生み出す3つの因子(V1、V2、V3)があり、1つの因子(V3)が単なるノイズであることがわかった場合、V3を無視するとX1とX2は冗長になる可能性があります。言い換えれば、X2がX1の単なる拡大縮小版であるならば、重要な因子(V1とV2)から見れば、それらは冗長です。
冗長性を厳密に測定するために、観測変数を潜在因子によって定義された空間内のベクトルとして捉えます。観測変数があれば、それを多次元空間のベクトルとして表現することができ、各次元は基本因子に対応します。これらのベクトルは、各変数と要因との関係を示しています。ベクトル間の角度は、変数が基盤となる因子について持っている情報の類似度を示します。角度が小さいほど、ベクトルがほぼ同じ方向を向いていることを意味し、冗長性が高いことを示します。言い換えれば、変数は似たような情報を提供します。
冗長性を定量化するためには、正規化されたベクトル(長さ1のベクトル)のドット積を使用します。このドット積の範囲は-1から1までで、ドット積が1の場合はベクトルが同一であることを意味し、完全な冗長性を示します。一方、-1の内積はベクトルが逆方向であることを意味し、一方を知れば他方の負を知ることができるため、冗長と考えることもできます。ドット積が0ということは、ベクトルが直交(独立)していることを意味し、冗長性がないことを示します。
観測された変数を基礎因子から計算する係数は、主成分を用いて求めることができます。支配的な主成分(大きな固有値を持つ)には通常、有用な情報のほとんどが含まれ、小さな固有値を持つ成分はノイズであることが多いです。因子と変数の相関を示す因子負荷行列は,主成分から標準化された観測変数を計算するために使用できます。実用的な目的のために、しばしば冗長性を測定するためにドット積の絶対値を取り、反対のベクトルも冗長性を示すことを認識します。 ベクトルを正規化することで、それらの長さが1になり、それらの間の角度の余弦を直接測ることができるようになります。
2つの変数が隠れた因子に関してどの程度関係しているかを計算するには、通常、まず重要と思われる主成分の数を決定しなければなりません。クラスタリングの計算は、因子負荷行列のこれらの列の最初のデータに焦点を当てます。これらの列の各行は、すべて足して1になるようにスケールが変更されます。2つの変数の間の類似度は,変換された因子負荷行列の対応する2つの行のドット積の絶対値になります。
次に、潜在因子との関係に基づき、非常に類似した変数をグループ化します。この際、優れた結果をもたらすことで知られている手法が、階層クラスタリングです。agglomerative hierarchical clustering (AHC)(英語)としても知られる階層クラスタリングでは、グループ化は、各変数を1つのメンバーを持つグループに割り当てることから始まります。可能性のあるすべてのグループのペアをテストし、最も近い2つを見つけます。これらのグループは1つのグループにまとめられています。このプロセスは、グループが1つになるか、類似度が過度に小さくなるまで繰り返されます。
AHCの実装はAlglibライブラリのMQL5ポートで提供されています。これは、カスタム距離指標を実装する機能をサポートしているため、ここでの目的に特に適しています。この機能は3つのAlglibクラスを通して提供されます。Alglibの階層的凝集型クラスタリングの実装を使用するには、処理結果を格納するCAHCReport構造体のインスタンスが必要です。CAHCReport m_rep;
CClusterizerStateクラスはクラスタ化エンジンをカプセル化します。これがなければクラスタリングはできません。
CClusterizerState m_cs;
このプロセスは、CClusteringクラスのスタティックメソッド'ClusterizerCreate()'を呼び出すことによって、クラスタ化エンジンを初期化することから始まります。
CClustering::ClusterizerCreate(m_cs);
初期化の後、CClusteringの他の静的メソッドを使用して、クラスタ化プロセスのパラメータを設定することができます。いずれも初期化されたクラスタ化エンジンを必要とします。
CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);
最後にClusterizerRunAHC()が実際の操作をトリガーします。
CClustering::ClusterizerRunAHC(m_cs,m_rep);
結果はCAHCReportインスタンスプロパティを通してアクセスできます。
前述したように、この作戦ではカスタム距離指標を実装します。これは、各変数(因子負荷量の行)の初期距離を持つ行列を提供することによって達成されます。以下のコードスニペットは、提供された荷重から初期距離がどのように計算されるかを示しています。
for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; }
まず、考慮する次元数に関して荷重を正規化します。
for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } }
そして、これらは距離の計算に使用されます。また、正規化された負荷量はクラスタライザーに渡されるものです。生の因子負荷量ではありません。クラスタリングを実装するコードはすべてCClusterクラスで与えられます。
//+------------------------------------------------------------------+ //| cluster a set of points | //+------------------------------------------------------------------+ class CCluster { private: CClusterizerState m_cs; CAHCReport m_rep; matrix m_pd[]; //+------------------------------------------------------------------+ //| Preprocesses input matrix before clusterization | //+------------------------------------------------------------------+ bool customDist(matrix &structure, ulong num_factors, matrix& out[], bool calculate_custom_distances = true) { int nvars; double dotprod, length; nvars = int(structure.Rows()); int ndim = (num_factors && num_factors<=structure.Cols())?int(num_factors):int(structure.Cols()); if(out.Size()<2) if(out.Size()<2 && (ArrayResize(out,2)!=2 || !out[0].Resize(nvars,ndim) || !out[1].Resize(nvars,nvars))) { Print(__FUNCTION__, " error ", GetLastError()); return false; } if(calculate_custom_distances) { for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; } out[1].Fill(0.0); for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } } } else { out[0] = np::sliceMatrixCols(structure,0,ndim); } return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CCluster(void) { CClustering::ClusterizerCreate(m_cs); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CCluster(void) { } //+------------------------------------------------------------------+ //| cluster a set | //+------------------------------------------------------------------+ bool cluster(matrix &in_points, ulong factors=0, ENUM_LINK_METHOD linkage=MODE_COMPLETE, ENUM_DIST_CRIT dist = DIST_CUSTOM) { if(!customDist(in_points,factors,m_pd,dist==DIST_CUSTOM)) return false; CMatrixDouble pp(m_pd[0]); CMatrixDouble pd(m_pd[1]); CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); if(dist==DIST_CUSTOM) CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage); CClustering::ClusterizerRunAHC(m_cs,m_rep); return m_rep.m_terminationtype==1; } //+------------------------------------------------------------------+ //| output clusters to vector array | //+------------------------------------------------------------------+ bool get_clusters(vector &out[]) { if(m_rep.m_terminationtype!=1) { Print(__FUNCTION__, " no cluster information available"); return false; } if(ArrayResize(out,m_rep.m_pz.Rows())!=m_rep.m_pz.Rows()) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int i = 0; i<m_rep.m_pm.Rows(); i++) { int zz = 0; for(int j = 0; j<m_rep.m_pm.Cols()-2; j+=2) { int from = m_rep.m_pm.Get(i,j); int to = m_rep.m_pm.Get(i,j+1); if(!out[i].Resize((to-from)+zz+1)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int k = from; k<=to; k++,zz++) out[i][zz] = m_rep.m_p[k]; } } return true; } };
cluster()関数は、与えられた入力点の集合に対して階層的クラスタリングをおこないます。この関数は、入力点の行列への参照、考慮する因子の数、使用する連結方法、距離基準の4つのパラメータを取ります。まず、指定された距離基準がカスタムであれば、カスタム距離行列を計算します。距離計算に失敗した場合、この関数はfalseを返します。次に、計算された距離データから2つの行列、ppとpdを初期化します。そして,この関数は,距離基準を用いてクラスタリングする点を設定します.距離基準がカスタムオプションに設定されていない場合,デフォルトはユークリッドです.距離基準がカスタムであれば,それに応じてクラスタリングのための距離を設定します.距離と点を設定した後,この関数は,指定された連結手法で階層クラスタリングアルゴリズムを構成します.これは凝集型階層クラスタリングアルゴリズムを実行し、クラスタリングプロセスの終了タイプを確認します。この関数は、クラスタリングが成功したことを示す終端タイプが1の場合はtrueを返し、そうでない場合はfalseを返します。
get_clusters()関数は、階層的クラスタリング処理の結果からクラスタを抽出して出力します。これは1つのパラメータを取ります。クラスタが格納されるベクトルout[]の配列です。この関数は、まずクラスタリングプロセスの終了タイプが1であるかどうかを確認します。そうでない場合はエラーメッセージを表示し、falseを返します。そして,この関数は,クラスタリング情報を含む行列m_rep.m_pmの各行を繰り返し処理します。各行に対して、出力ベクトルのインデックスを追跡するための変数zzを初期化します。そして、現在の行の列を繰り返し、列のペア(クラスタの開始インデックスと終了インデックスを表す)を処理します。各対について、インデックスの範囲(fromからtoまで)を計算し、クラスタ要素に対応するように現在の出力ベクトルのサイズを変更します。サイズ変更に失敗した場合は、エラーメッセージを表示してfalseを返します。最後に、この関数は現在の出力ベクトルをクラスタの要素で埋め、fromからtoを繰り返し、各要素に対してzzをインクリメントします。処理が正常に完了した場合、この関数は真を返し、クラスタが正常に抽出され、out配列に格納されたことを示します。
以下のコードスニペットは、CClusterクラスの使い方を示しています。
vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); }MetaTrader 5には、凝集型階層クラスタリング(AHC)の結果を直接可視化するツールがありません。ターミナルのコンソールはある程度の出力を表示できるが、AHCのような複雑な結果を見るには使い勝手が悪いです。AHCの結果は、データのグループ化の階層構造を示すデンドログラムによって最もよく可視化されます。デンドログラムは、データポイントまたはクラスタを段階的に結合することによって、クラスタがどのように形成されるかを示しています。以下は、私たちの指標データセットのグループ分けを手作業で描いたデンドログラムです。
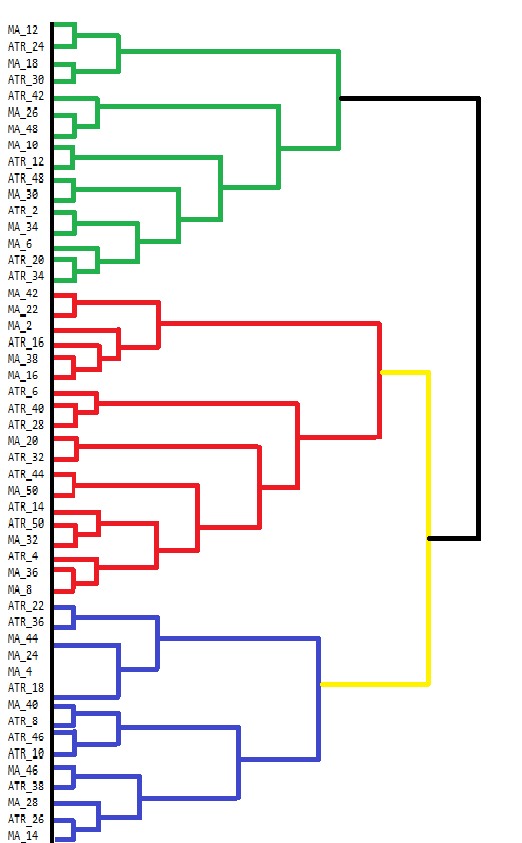
デンドログラムは、互いに似ている変数のクラスタを示しています。より低いレベル(デンドログラムの底に近い)で結合される変数は、より高いレベルで結合される変数よりも互いに類似しています。例えば、MA_12とMA_24はATR_18と比較してより類似しています。デンドログラムは、異なるクラスタを示すために異なる色を使用します。緑、赤、青、黄色のクラスタは、密接に関連している変数のグループを強調しています。各色は、高い類似性または冗長性を示す変数の集合を表します。
2つのクラスタが合体する高さは、クラスタ間の非類似度を示します。高さが低いほど、クラスタは似ています。上部の黒い結合のように、より高いレベルで結合しているクラスタは、これらのクラスタ間でより大きな違いがあることを示しています。この階層的なクラスタリングは、変数選択の決定に役立ちます。クラスタを分析することで、各クラスタ内の特定の代表的な変数に焦点を当ててさらに分析することを決定し、重要な情報を失うことなくデータセットを単純化することができます。
指標データセットの収集と分析に使用されるMQL5コードは、スクリプトEDA.mq5に含まれています。この記事では、pfa.mqhで定義されているすべてのコードツールを使用しています。
//+------------------------------------------------------------------+ //| EDA.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\Slope.ex5" #resource "\\Indicators\\CMMA.ex5" #include<pfa.mqh> #include<ErrorDescription.mqh> #property script_show_inputs //+------------------------------------------------------------------+ //|indicator type | //+------------------------------------------------------------------+ enum SELECT_INDICATOR { CMMA=0,//CMMA SLOPE//SLOPE }; //--- input parameters input uint period_inc=2;//lookback increment input uint max_lookback=50; input ENUM_MA_METHOD AppliedMA = MODE_SMA; input datetime SampleStartDate=D'2019.12.31'; input datetime SampleStopDate=D'2022.12.31'; input string SetSymbol="BTCUSD"; input ENUM_TIMEFRAMES SetTF = PERIOD_D1; input ENUM_FACTOR_ROTATION AppliedFactorRotation = MODE_PROMAX; input ENUM_DIST_CRIT AppliedDistanceCriterion = DIST_CUSTOM; input ENUM_LINK_METHOD AppliedClusterAlgorithm = MODE_COMPLETE; input ulong Num_Dimensions = 10; //---- string csv_header=""; //csv file header int size_sample, //training set size size_observations, //size of of both training and testing sets combined maxperiod, //maximum lookback indicator_handle=INVALID_HANDLE; //long moving average indicator handle //--- vector indicator[]; //indicator indicator values; //--- matrix feature_matrix; //full matrix of features; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //---get relative shift of sample set int samplestart,samplestop,num_features; samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate); samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate); num_features = int((max_lookback/period_inc)*2); //---check for errors from ibarshift calls if(samplestart<0 || samplestop<0) { Print(ErrorDescription(GetLastError())); return; } //---set the size of the sample sets size_observations=(samplestart - samplestop) + 1 ; maxperiod=int(max_lookback); //---check for input errors if(size_observations<=0 || maxperiod<=0) { Print("Invalid inputs "); return; } //---allocate memory if(ArrayResize(indicator,num_features)<num_features) { Print(ErrorDescription(GetLastError())); return; } //----get the full collection of indicator values int period_len; int k=0; //--- for(SELECT_INDICATOR select_indicator = 0; select_indicator<2; select_indicator++) { for(int iperiod=0; iperiod<int(indicator.Size()/2); iperiod++) { period_len=int((iperiod+1) * period_inc); int try=10; while(try) { switch(select_indicator) { case CMMA: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\CMMA.ex5",AppliedMA,period_len); break; case SLOPE: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\Slope.ex5",period_len); break; } if(indicator_handle==INVALID_HANDLE) try--; else break; } if(indicator_handle==INVALID_HANDLE) { Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError()); return; } Comment("copying data to buffer for indicator ",period_len); try = 0; while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try<10) { try++; Sleep(5000); } if(try<10) ++k; else { Print("error copying to indicator buffers ",GetLastError()); Comment(""); return; } if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle)) indicator_handle=INVALID_HANDLE; } } //---resize matrix if(!feature_matrix.Resize(size_observations,indicator.Size())) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //---copy collected data to matrix for(ulong i = 0; i<feature_matrix.Cols(); i++) if(!feature_matrix.Col(indicator[i],i)) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //--- Comment(""); //---test dataset for principal factor analysis suitability //---kmo test vector kmo_vect; double kmo_stat; kmo(feature_matrix,kmo_vect,kmo_stat); Print("KMO test statistic ", kmo_stat); //---Bartlett sphericity test double bs_stat,bs_pvalue; bartlet_sphericity(feature_matrix,bs_stat,bs_pvalue); Print("Bartlett sphericity test p_value ", bs_pvalue); //---Extract the principal factors Cpfa fa; //--- if(!fa.fit(feature_matrix)) return; //--- matrix fld = fa.get_factor_loadings(); //--- matrix rotated_fld = fa.rotate_factorloadings(AppliedFactorRotation); //--- Print(" factor loading matrix ", fld); //--- Print("\n rotated factor loading matrix ", rotated_fld); //--- matrix egvcts; vector egvals; fa.get_eigen_structure(egvcts,egvals,false); Print("\n vects ", egvcts); Print("\n evals ", egvals); //--- vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); } } //+------------------------------------------------------------------+
時系列のコヒーレンス
時系列で変数を分析する場合、その関係は予想外に変化することがあります。通常、相関のある変数が突然乖離することがあり、これは潜在的な問題の兆候であるかもしれません。例えば、気温の変化は電力需要に影響を与え、それが天然ガス価格に影響を与えます。いつものパターンが変わったら、何か異常が起きているのかもしれません。同様に、通常は独立して行動する変数が突然一緒に動くこともあります。例えば、株式市場の異なるセクターがポジティブな経済ニュースによって同時に上昇した場合などです。
コヒーレンスの測定は、時系列変数のセットが移動する期間の中でどの程度関連しているかを定量化するものです。1つの基本的な方法は、最大の固有値がどれだけの分散を捕捉しているかを評価することです。しかし、この方法は1つの次元しか考慮しないため、限界があります。より包括的なアプローチは、特に変数間に複数の関係が存在する場合に、最大の固有値を合計することです。このアプローチは、複雑な相互関係を持つシステムの全体的な一貫性をより正確に把握することができますが、最も関連性の高い要因を事前に把握しておく必要があります。それは不可能かもしれないし、単に主観的すぎるだけかもしれません。
関係の数が未知であったり、時間とともに変動するようなシナリオ、特に変数の数が多い場合には、より一般的なアプローチが必要となります。未知の次元を持つシナリオでは、固有値を大きいものから小さいものへと並び替え、オーケストラのメンバーのように視覚化することができます。美しい音楽を生み出す鍵は、さまざまな楽器を統一的に調和させることにあります。オーケストラの個々のメンバーが適切なレベルで団結してついていけなければ、出来上がる音楽はひどいものになります。結束力は低いでしょう。オーケストラの各メンバーの音の出力を、聴衆が聴く音楽に貢献する加重値として想像してみてください。これらの値のアンバランスがコヒーレンスを表しています。加重合計を計算し、重みは楽器が生産できる量を示します。
各楽器(変数)が独立してそれぞれの曲を演奏している場合、全体的な音は無秩序で混沌としており、コヒーレンスがゼロであることを表しています。しかし、楽器が完全に同期し、ハーモニーを奏でるとき、完全なコヒーレンスを表す、まとまりのある美しい音楽が生まれます。この例えのコヒーレンスは、オーケストラのハーモニーのようなもので、楽器(変数)がどれだけうまく調和して演奏できているかを示しています。和声が突然変化する場合は、楽器や作曲に何か異常が起きていることを示唆しています。
両極端を考えてみましょう。変数が完全に独立している場合。これらの変数の相関行列は恒等行列となり、すべての固有値は等しくなります(1.0)。加重和は(対称加重のため)ゼロとなり、コヒーレンスはゼロとなります。あるいは、変数間に完全な相関がある場合は、変数の数と同じだけ、ゼロでない固有値が存在します。重み付けされた合計が変数の数となり、正規化(変数の数で割る)後のコヒーレンスは1.0となり、完全な相関を反映します。この方法は、次元に関する仮定をすることなく、固有値分布の不均衡に基づいてコヒーレンスの0-1の尺度を提供します。
コヒーレンスを説明するために、時間窓内の異なる銘柄の終値のコヒーレンスを測定する指標を作成します。この指標はCoherence.mq5と呼ばれます。コンマで区切られた楽器名のリストとして追加することで、ユーザーは多数の銘柄間の結合度を測定できるようになります。この指標は、複数の変数間の相関を計算するために異なるアプローチを採用しています。今回はスピアマンスノンパラメトリック相関係数を用います。
covar[0][0] = 1.0 ; for(int i=1 ; i<npred ; i++) { for(int j=0 ; j<i ; j++) { for(int k=0 ; k<lookback ; k++) { nonpar1[k] = iClose(stringbuffer[i],PERIOD_CURRENT,ibar+k); nonpar2[k] = iClose(stringbuffer[j],PERIOD_CURRENT,ibar+k); } if(!MathCorrelationSpearman(nonpar1,nonpar2,covar[i][j])) Print(" MathCorrelationSpearman failed ", GetLastError(), " :", ibar); } covar[i][i] = 1.0 ; }
AglibのEVD実装を使用しているため、相関行列全体を定義する必要はなく、上三角形または下三角形を構築するだけで済みます。固有ベクトルは必要なく、固有値だけが必要なのです。
CMatrixDouble cdata(covar); if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Rows(),0,false,evals,evects)) { Print(" EVD failed ", GetLastError(), " :", ibar); coherenceBuffer[ibar]=0.0; continue; }
固有値の分布を正しい方向にするためには、ベクトルを反転させなければなりません。
vector eval = evals.ToVector(); if(!np::reverseVector(eval)) Print(" failed vecter reversal operation : ", ibar);
凝集力は固有値を使用して計算されます。
double center = 0.5 * (npred - 1) ; double sum = 0.0; for(ulong i=0 ; i<eval.Size() ; i++) { sum += (center - i) * eval[i] / center ; } coherenceBuffer[ibar] = sum / eval.Sum();
完全なコードは記事の最後に添付されています。暗号通貨BTCUSD,DOGUSD,XRPUSD間のコヒーレンスを測定することで、異なるウィンドウの長さの指標がどのように見えるかを見てみましょう。
コヒーレンスの60日間のプロットを見ると、これらの銘柄は注目に値する一貫性を持って動いているという個人的な先入観を払拭することができました。驚くのは、その変動幅の大きさです。値は可能な限りあらゆる範囲にわたって変化します。
期間が長くなるにつれて、コヒーレンスが安定する時期が見え始めますが、このコヒーレンスの性質はまた予想外のものです。ほとんどコヒーレンスがない期間がかなりあります。
結論
これらの高度なテクニックにおける固有値と固有ベクトルの活用は、データサイエンスにおけるその汎用性と基本的な重要性を強調しています。固有値と固有ベクトルは、次元削減、パターン認識、そして複雑なデータセット内の潜在的な構造の発見において、堅牢なフレームワークを提供します。PCAを超えることで、私たちはより豊かな洞察を得るための、ニュアンスの異なるツールセットを手に入れることができます。このテキストは、固有ベクトルと固有値が数学的抽象をはるかに超えたものであり、現代のトレーダーが優位に立つために活用できる洗練された分析手法の基礎であることを示しています。記事内で紹介したすべてのコードは、圧縮されたアーカイブファイルに添付されています。以下の表は、ダウンロード可能なファイルの一覧です。| ファイル | 詳細 |
|---|---|
| Mql5\Include\np.mqh | 様々な行列とベクトル関数のユーティリティを含むインクルードファイル |
| Mql5\Include\pfa.mqh | pfa.mqhでは、Cpfaクラス、CClusterクラス、CRotatorクラスの定義とKMOとBTSの試験実装のための関数定義を提供 |
| Mql5\Scripts\EDA.mq5 | このスクリプトは、主因子分析のためのカスタム指標のデータセットを収集することで、記事で説明されているすべてのコードツールの使用を実証する |
| Mql5\Scripts\TestEigenDecomposition.mq5 | このスクリプトは、組み込まれた'Eig()'行列メソッドに関して、言及された問題を再現する |
| Mql5\Indicators\Coherence.mq5 | 3つの銘柄に適用されるコヒーレンス指標。 |
| Mql5\Experts\PrincipalFactors.mq5 | 大きな行列を表示するために参照されるアプリケーションのソースコードです。このコードは、MQL5のコードベースにある由緒あるEasy and Fast GUIライブラリに依存しています。 |
| Mql5\Experts\PrincipalFactors.ex5 | これは上記のリストを編集したものです。 |
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15229
 知っておくべきMQL5ウィザードのテクニック(第27回):移動平均と迎角
知っておくべきMQL5ウィザードのテクニック(第27回):移動平均と迎角
 Pythonを使ったEAとバックテストのための感情分析とディープラーニング
Pythonを使ったEAとバックテストのための感情分析とディープラーニング
 スマートマネーコンセプト(BOS)とRSI指標をEAに統合する方法
スマートマネーコンセプト(BOS)とRSI指標をEAに統合する方法
 知っておくべきMQL5ウィザードのテクニック(第26回):移動平均とハースト指数
知っておくべきMQL5ウィザードのテクニック(第26回):移動平均とハースト指数
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索