Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет. Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Mathemat>>: Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет. Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Компьютер подсчитал :) Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза). Действительно все решения содержат гирьку с весом 1.
Mathemat>>: Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь? Ага, слезно просим программку.
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32 - 単一回答
いずれかの重量が2^nより小さい場合、総重量は63より小さくなる。
それ以上だと、このケトルベルで得られるウェイトの順番にズレが生じます。
面白いことに、重りを両方のカップに同時に乗せることができれば、この問題はかなり難しく、興味深いものになります。 それこそ拷問したいくらいだ。
いずれにしても重みの最小値が1であることは判明しているが。しかし、これは自動的に2.の程度に行くことを意味するものではありません。
次(10日)。
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
最小のケトルベル1がよくわからない
ケトルベル2個と3個でもいいかもしれませんね。
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
コンピュータが計算してくれたんだ :)
両方のカップに同時に重りを乗せることができれば、この問題の解は2136通り(ちょうど63個の重りがバランスできる)。
実際、すべての解に1の重みが含まれています。
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
プログラムは掲載されるのですか?お願い、お願い!
そう、涙ながらにプログラムをお願いするのです。
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
1について勘違いしていた。
プログラムには何の面白みもない、単純なオーバーシュートだ。
#include <stdio.h> (英語版のみ
#定義 COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){.
bool arr[COUNT]。
for(int i=0;i<COUNT;i++) arr[i]=falseとする。
// 1 - 1つのカップに、0 - 重さは関係ない -1 - 2番目のカップに
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++){.
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if(ves > COUNT) return false;
if(ves>0) arr[ves-1]=true;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) return false;
が真を返す。
}
main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d</n",i0,i1,i2,i3,i4,i5);
}
Следующая (10-й):
証明はあまり厳密でなくとも、正しい。
ここで、図のような頂点座標の表記を紹介しよう。青が正方形であるために
x1-x2=y1-y4 ;
y1-y2=x1-x2です。
のみならず
x3-x4=y2-y3です。
y4-y3=x2-x3です。
最初の2つの式から、グラフの式を思い出すと、次のようになる。
x4-x2=A(sinx2-sinx4),
さんせいよんせい
x3-x1=A(sinx1-sinx3).
最小の正方形数以外には制約がないため、ここでは原点について対称な正方形の場合のみを考えることにする。しかし、そうするとx4=-x2、x3=-x1となり、サインも同じになります。私たちの方程式は、このような形になります。
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
左辺に立つx2、x1から関数のグラフを思い出してください。グラフは、正のxと負のxの両方で極値を減少させています。明らかに、Aの数を徐々に減らしていくことで、1978以上の根を必要な数だけ得ることができる。
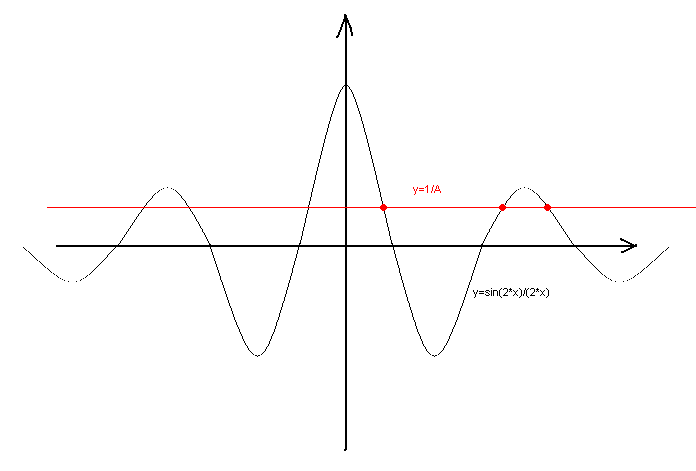
得られた根は異なっており、純粋に非合理的な方法で互いに関連している。この場合の二乗が対等でないことは、詳しく証明する必要はないだろう。