知っておくべきMQL5ウィザードのテクニック（第12回）：ニュートン多項式

はじめに

時系列分析は、ファンダメンタルズ分析をサポートするだけでなく、FXのような流動性の高い市場では、市場でのポジションの建て方を決定する主な原動力となることもあり、重要な役割を果たしています。伝統的なテクニカル指標は相場に大きく遅れをとる傾向があり、多くのトレーダーにとって敬遠されがちでした。おそらく、現時点で最も主流となっているのはニューラルネットワークですが、多項式補間はどうでしょう。

多項式補間は、過去の観測結果と将来の予測との関係を単純な式で明示的に示すため、理解しやすく実装しやすいという利点があります。これは、過去のデータが将来の値にどのような影響を与えるかを理解するのに役立ち、ひいては研究された時系列の振る舞いに関する幅広い概念や可能性のある理論を発展させることにつながります。

さらに、線形と二次関係の両方に適応可能であるため、様々な時系列に柔軟に対応でき、おそらくトレーダーにとってはより適切で、異なる市場タイプ（レンジ相場とトレンド相場、ボラティリティの高い相場と落ち着いた相場など）に対応できます。

さらに、ニューラルネットワークのような代替アプローチと比較すると、一般的に計算量が多くなく、比較的軽量です。実際、この記事で検討したモデルは、例えばニューラルネットワークで各訓練セッションの後に最適な重みとバイアスを保存しておく必要があるような、アーキテクチャに依存したストレージ要件はゼロです。

正式には、ニュートン補間N(x)は次の式で定義されます。

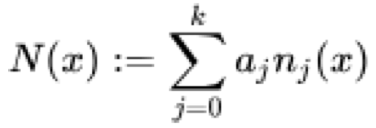
ここで、すべてのxjは級数内で一意であり、a jは差商の和、n j (x)はxの基底係数の積位相であり、正的には以下のように表されます。

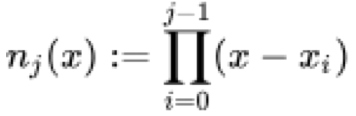
差商と基底係数の公式は、単独で簡単に調べることができますが、ここではできるだけ非公式にその定義を紐解いてみましょう。

差商は、与えられたデータセットからすべての被除数xがなくなるまで、各被除数にxの係数を設定する除算の繰り返しです。これを説明するために、3つのデータのサンプルを考えてみましょう。

(1,2)、(3,4)、(5,6)です。

差商が使用されるためには、すべてのx値が一意である必要があります。提供されたデータポイントの数によって、ニュートン形式の多項式で導き出されるxの最高指数が推測されます。例えば、2点しかない場合、方程式は単純に一次方程式になります。

y = mx + c

この場合、最高指数は1です。したがって、この3点の例では、最高指数は2であり、導出される多項式のために3つの異なる係数を得る必要があることを意味します。

これら3つの係数をそれぞれ求めるのは、3つ目にたどり着くまで一歩一歩の繰り返し作業です。上記のリンクにも計算式がありますが、これを理解するには、以下のような表を使うのが一番でしょう。

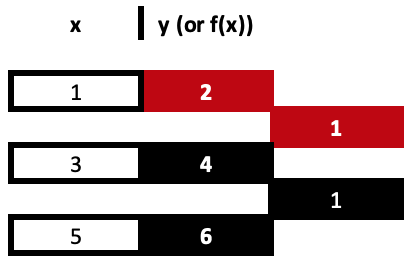
つまり、差商の最初の列は、y値の差を x値の差で除算することで得られます。すべてのx値は一意である必要があることを忘れないでください。これらの計算は非常にシンプルで簡単なものですが、共有リンクで紹介されている典型的な計算式ではなく、上記のような表から簡単におこなうことができます。どちらのアプローチも同じ結果につながります。

= (4 - 2) / (3 - 1)

では、最初の係数は1です。

= (6 - 4) / (5 - 3)

は、同じ値の2番目の係数です。係数は赤で強調表示されています。

3つのデータポイントの例では、最終的な値は、計算された値からyの差を得ますが、xの分母は

x系列の2つの極値であり、その差が除数となるため、表は次のようになります。

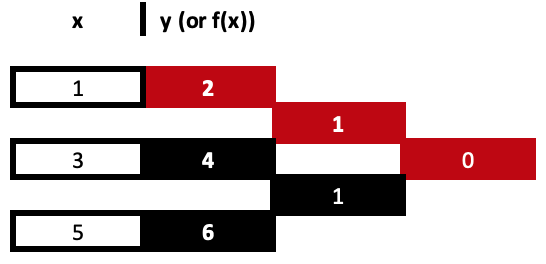
上記の表を完成させると、3つの導出値がありますが、係数を求めるのに使用されるのはそのうちの2つだけです。こうして「基底関数」の積和が導かれます。すごいように聞こえるかもしれませんが、これは実に簡単なことです。差商よりも簡単です。つまり、上の表から導き出された係数を基に、3点に対する方程式を説明すると、次のようになります。

y = 2 + 1*(x – 1) + 0*(x – 1)*(x – 3)

つまり

y = x + 1

括弧を加えたものが基底関数を構成するすべてです。x n値は、単にサンプリングされた各データポイントのそれぞれのx値です。ここで係数に戻ります。原則として、これらの括弧の値の前に表上部の値のみを使用し、表内の列を短くして右に進むにつれて、提供されたすべてのデータ ポイントが考慮されるまで、上部の値は長い括弧の列の前に付けられます。前述したように、補間するデータポイントが多ければ多いほど、xの指数が増えるので、導出表の列数も増えます。

実装に移る前に、もう1つ魅力的な説明をしておきましょう。下図のように、7つの証券価格のデータポイントがあり、xの値は単に価格バーインデックスであるとします。

0	1.25590
1	1.26370
2	1.25890
3	1.25395
4	1.25785
5	1.26565
6	1.26175

係数値を伝播する表は、以下のように8列分拡張されます。

<table:8 columns of divided differences />

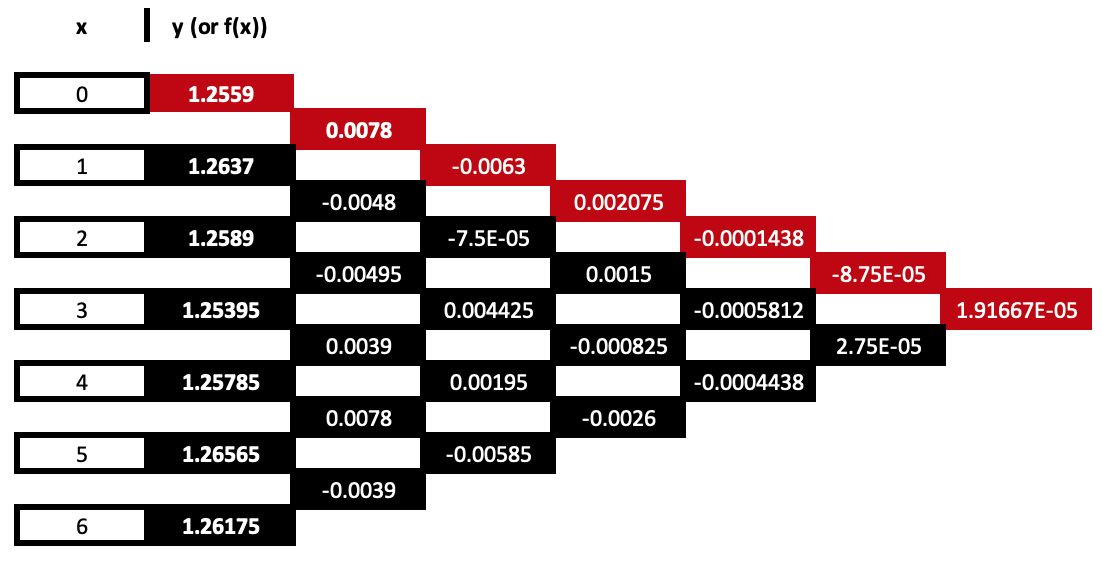
係数を赤で強調すると、この式は次のようになります。

y = 1.2559 + 0.0078*(x – 0) – 0.0063*(x – 0)*(x – 1) + …

この方程式は、7つのデータポイントから指数6まで上がることは明らかです。その重要な機能は、方程式に新しいxインデックスを入力することによって次の値を予測することであることは間違いありません。サンプリングされたデータが「系列として設定」されていれば、次のインデックスは-1、そうでなければ8となります。

MQL5の実装

MQL5でこれを実装するのには最小限のコーディングで可能ですが、例えば、あらかじめコーディングされたクラスインスタンスからこのようなアイデアを実行できるようなライブラリは見つかりませんでした。

しかし、これを実現するためには、基本的に2つのことが必要です。まず、サンプリングされたデータセットから方程式の係数xを計算する関数が必要です。第二に、x値が提示されたときに、式を用いて予測値を処理する関数も必要です。これはとても簡単なことのように聞こえますが、スケーラブルな方法でこれをおこないたいことを考慮すると、処理ステップにおけるいくつかの注意点に留意する必要があります。

本題に入る前に、「スケーラブルな方法」とは何を意味するのでしょうか。これは単に、大きさがあらかじめ決まっていないデータセットに対して、差商を用いて係数を求めることができる関数を指しています。当たり前のことのように聞こえるかもしれませんが、最初の3データポイントの例を考えてみると、係数を求めるためのMQL5の実装は次のようになります。

以下のコードは、単純にサンプリングされたデータ内の2つのペアの差商を得るための方程式に従い、最後の値も得るためにこの手順を反復します。ここで、もし4点のデータサンプルがあったとしたら、その方程式を補間するには、上の3点の例で示したものよりもステップ数が増えるので、別の関数が必要になります。

つまり、スケーラブルな関数があれば、n個のデータセットを扱い、n-1個の係数を出力できることになります。これは以下のコードによって実現しました。

//+------------------------------------------------------------------+
//| INPUT PARAMETERS                                                 |
//|     X   -   vector with x values of sampled data                 |
//|     Y   -   vector with y values of sampled data                 |
//| OUTPUT PARAMETERS                                                |
//|     W   -   vector with coefficients.                            |                                          |
//+------------------------------------------------------------------+
void Cnewton::Set(vector &W, vector &X, vector &Y)
{  vector _w[];
   ArrayResize(_w, int(X.Size() - 1));
   int _x_scale = 1;
   int _y_scale = int(X.Size() - 1);
   for(int i = 0; i < int(X.Size() - 1); i++)
   {  _w[i].Init(_y_scale);
      for(int ii = 0; ii < _y_scale; ii++)
      {  if(X[ii + _x_scale] != X[ii])
         {  if(i == 0)
            {  _w[i][ii] = (Y[ii + 1] - Y[ii]) / (X[ii + _x_scale] - X[ii]);
            }
            else if(i > 0)
            {  _w[i][ii] = (_w[i - 1][ii + 1] - _w[i - 1][ii]) / (X[ii + _x_scale] - X[ii]);
            }
         }
         else
         {  printf(__FUNCSIG__ + " ERR!, identical X value: " + DoubleToString(X[ii + _x_scale]) + ", at: " + IntegerToString(ii + _x_scale) + ", and: " + IntegerToString(ii));
            return;
         }
      }
      _x_scale++;
      _y_scale--;
      W[i + 1] = _w[i][0];
      if(_y_scale <= 0)
      {  break;
      }
   }
}

この関数は、2つの入れ子になったforループと、x値とy値のインデックスを追跡する2つの整数を使用して動作します。最も効率的な実装方法ではないかもしれませんが機能します。これを実装した標準ライブラリがないので、これを探求してユースケースによっては改良を加えることをお勧めします。

xの入力とすべての方程式係数が与えられたときに、次のyを処理する関数も以下で共有します。

//+------------------------------------------------------------------+
//| INPUT PARAMETERS                                                 |
//|     W   -   vector with pre-computed coefficients                |
//|     X   -   vector with x values of sampled data                 |
//|     XX  -   query x value with unknown y                         |
//| OUTPUT PARAMETERS                                                |
//|     YY  -   solution for unknown y.                              |  
//+------------------------------------------------------------------+
void Cnewton::Get(vector &W, vector &X, double &XX, double &YY)
{  YY = W[0];
   for(int i = 1; i < int(W.Size()); i++)
   {  double _y = W[i];
      for(int ii = 0; ii < i; ii++)
      {  _y *= (XX - X[ii]);
      }
      YY += _y;
   }
}

この関数もネストされたループを持ちますが、先の関数より単純明快です。ここでやっていることは、set関数で得た係数を追跡し、適切なニュートン基底多項式に割り当てることだけです。

応用

応用は多岐にわたりますが、今回はシグナル、トレール注文法、資金管理法としてどのように使用できるかを考えてみたいと思います。これらをコーディングする前に、通常、補間機能を実装した2つの関数を持つアンカークラスを用意するのがよいです。このようなクラスのインターフェイスは次のようになります。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnewton
{
private:

public:
                     Cnewton();
                    ~Cnewton();
   void              Set(vector &W, vector &X, vector &Y);
   void              Get(vector &W, vector &X, double &XX, double &YY);
};

シグナル

MQL5ライブラリで提供される標準EAシグナルクラスファイルは、カスタム実装を開発する際の健全なガイドとして常に役立ちます。私たちの場合、多項式を生成するための入力サンプルデータとして、最初に選ぶべきなのは、生の証券終値でしょう。終値から多項式を生成するには、まずxとyのベクトルにそれぞれ棒グラフのインデックスと実際の終値を入れます。これら2つのベクトルは、係数を取得するためのset関数の重要な入力となります。余談ですが、ここではシグナル内のxに価格バーインデックスを使用しているだけですが、取引日や取引週のセッションなどを代わりに使用することも可能です。ただし、もちろんデータサンプル内でこれらが繰り返されない（つまりすべて1回だけ出現する）場合のみです。取引日に4つのセッションがある場合、提供できるデータポイントは4つまでであり、セッション指標0、1、2、3はデータセット内に1回だけ登場することができます。

xとyのベクトルを埋めた後、set関数を呼び出せば、多項式の予備係数が得られるはずです。これらの係数と次のx値を使用してこの方程式をget関数で実行すると、次のy値がどうなるかの投影が得られます。set関数の入力y値は終値なので、次の終値を求めることになります。コードを以下に紹介します。

   double _xx = -1.0;//m_length + 1.0,
   double _yy = 0.0;
   __N.Get(_w, _xx, _yy);

EAシグナルクラスの確認オープン関数は、次の終値予想値を取得することに加え、通常、売買シグナルの強さを示す0～100の範囲の整数を出力します。したがって、このケースでは、予想終値をこの範囲に収まる単純な整数として表す方法を見つける必要があります。

この正規化をおこなうために、予想終値の変化を現在の高値-安値のレンジに対するパーセンテージで表します。このパーセンテージは0～100の整数で表されます。このことは、「check for open long」関数におけるマイナスの終値の変化は自動的にゼロになることを意味し、「check for open short」関数におけるプラスの予測変化も同様にゼロになることを意味します。

   m_high.Refresh(-1);
   m_low.Refresh(-1);
   m_close.Refresh(-1);
   int _i = StartIndex();
   double _h = m_high.GetData(m_high.MaxIndex(_i,m_length));
   double _l = m_low.GetData(m_low.MinIndex(_i,m_length));
   double _c = m_close.GetData(0);
//
   if(_yy > _c)
   {  _result = int(round(((_yy - _c) / (fmax(_h, fmax(_yy, _c)) - fmin(fmin(_yy, _c), _l))) * 100.0));
   }

多項式を使用した予測では、使用する変数はルックバック期間の長さだけです（これはサンプリングデータのサイズを設定する）。この変数にはm_lengthというラベルが付けられています。銘柄EURJPYについて、2023年の1時間足でこのパラメータのみの最適化を実行すると、以下のレポートが得られます。

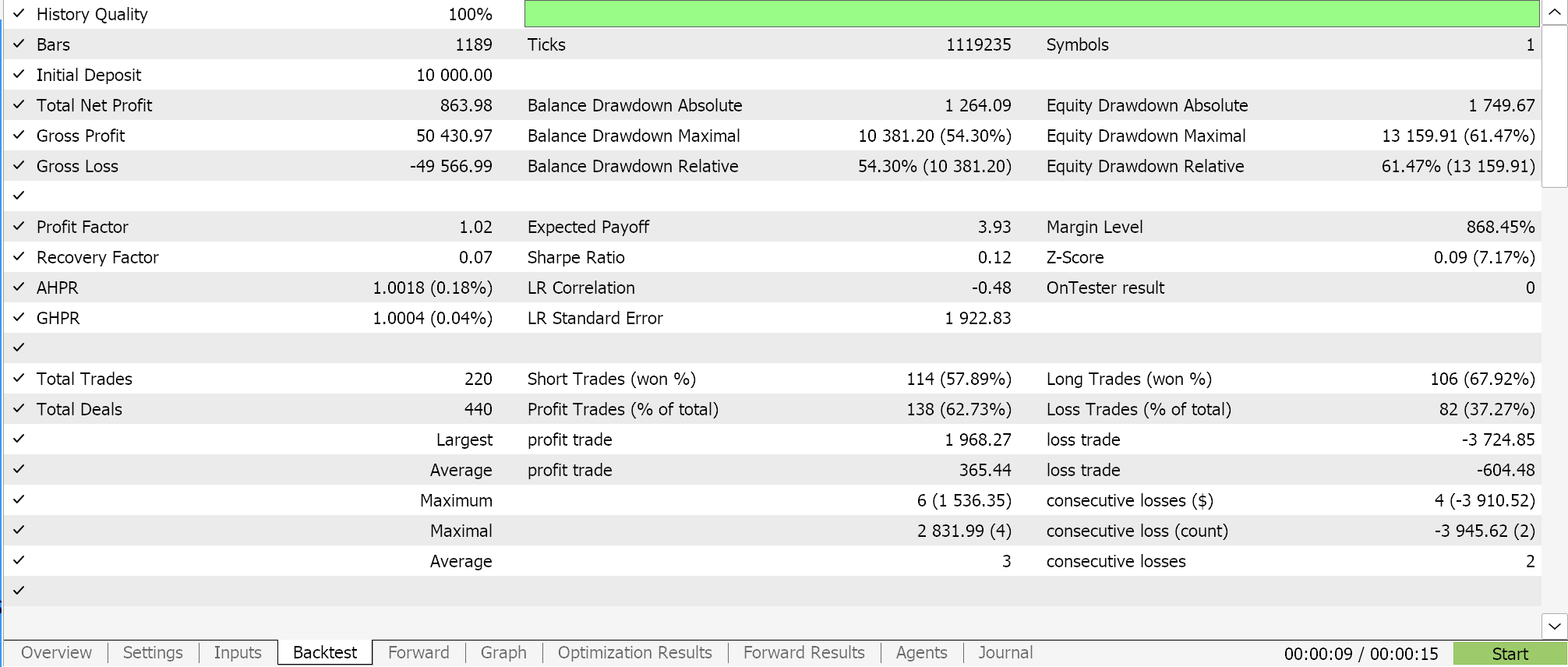
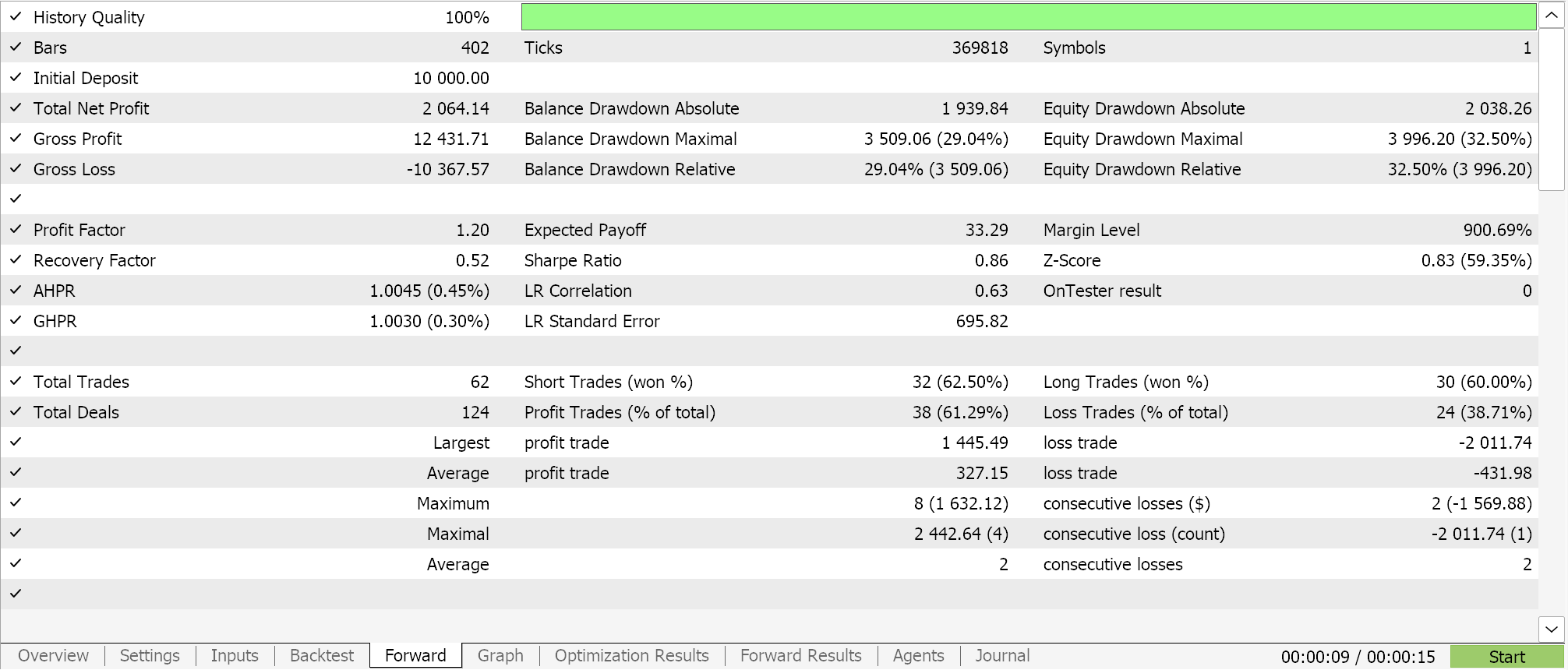
年間を通した完全な実行によって、このようなエクイティは次のようになります。

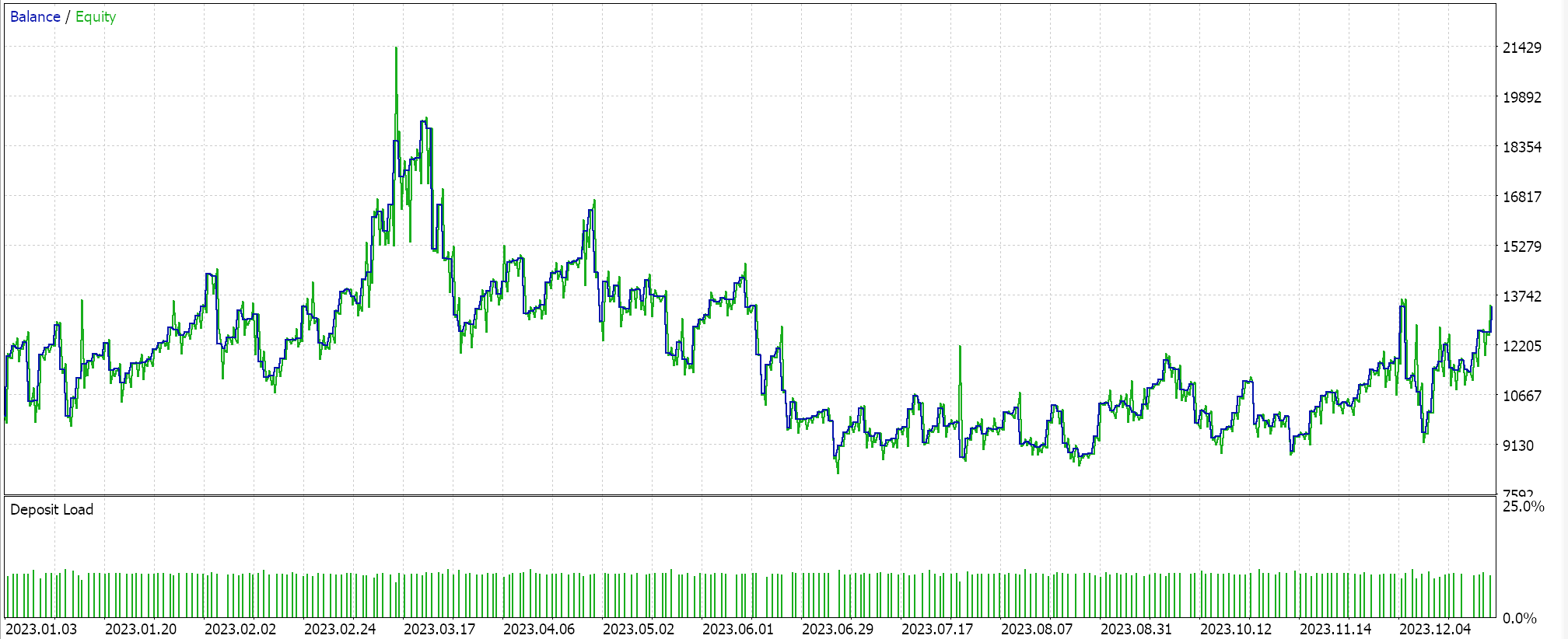
トレール注文

EAシグナルクラスの他に、未決済ポジションのトレール注文の設定と調整方法を選択することで、ウィザードを使用してEAを組み立てることができます。ライブラリには、Parabolic SARと移動平均を使うメソッドが用意されていますが、全体として、その数はシグナルライブラリにあるものよりはるかに少ないです。ニュートン多項式を使用するクラスを追加することによってこのカウントを改善するのであれば、サンプリングされたデータは間違いなく価格バーの範囲でなければなりません。

従って、次の終値を予測するときと同じステップを踏むとすると、主な変更点はyベクトルのデータで、この場合は価格バーの範囲となります。ソースは次のようになります。

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingNP::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

   ...

//---
   m_high.Refresh(-1);
   m_low.Refresh(-1);
   vector _x, _y;
   _x.Init(m_length);
   _y.Init(m_length);
   for(int i = 0; i < m_length; i++)
   {  _x[i] = i;
      _y[i] = (m_high.GetData(StartIndex()+i)-m_low.GetData(StartIndex()+i));
   }
   vector _w;
   _w.Init(m_length);
   _w[0] = _y[0];
   __N.Set(_w, _x, _y);
   double _xx = -1.0;
   double _yy = 0.0;
   __N.Get(_w, _x, _xx, _yy);
//---

   ...

//---
   return(sl != EMPTY_VALUE);
}

その後、この予測バーレンジの割合を使用して、ポジションの損切りの大きさを設定します。使用される割合は最適化可能なパラメータm_stop_levelであり、新しい損切りが設定される前に、証券会社のエラーを避けるために、このデルタにストップ距離の最小値を加えます。この正規化は以下のコードでキャプチャされます。

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingNP::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check
   
   ...

//---
   sl = EMPTY_VALUE;
   tp = EMPTY_VALUE;
   delta = (m_stop_level * _yy) + (m_symbol.Point() * m_symbol.StopsLevel());
//---
   if(price - base > delta)
   {  sl = price - delta;
   }
//---
   return(sl != EMPTY_VALUE);
}

ライブラリのAwesome Oscillator EAシグナルクラスを使用するEAをMQL5ウィザードを使用して組み立て、上記と同じ銘柄、時間枠、1年の期間について、理想的な多項式の長さについてのみ最適化を試みると、最良のケースとして以下のレポートが得られます。

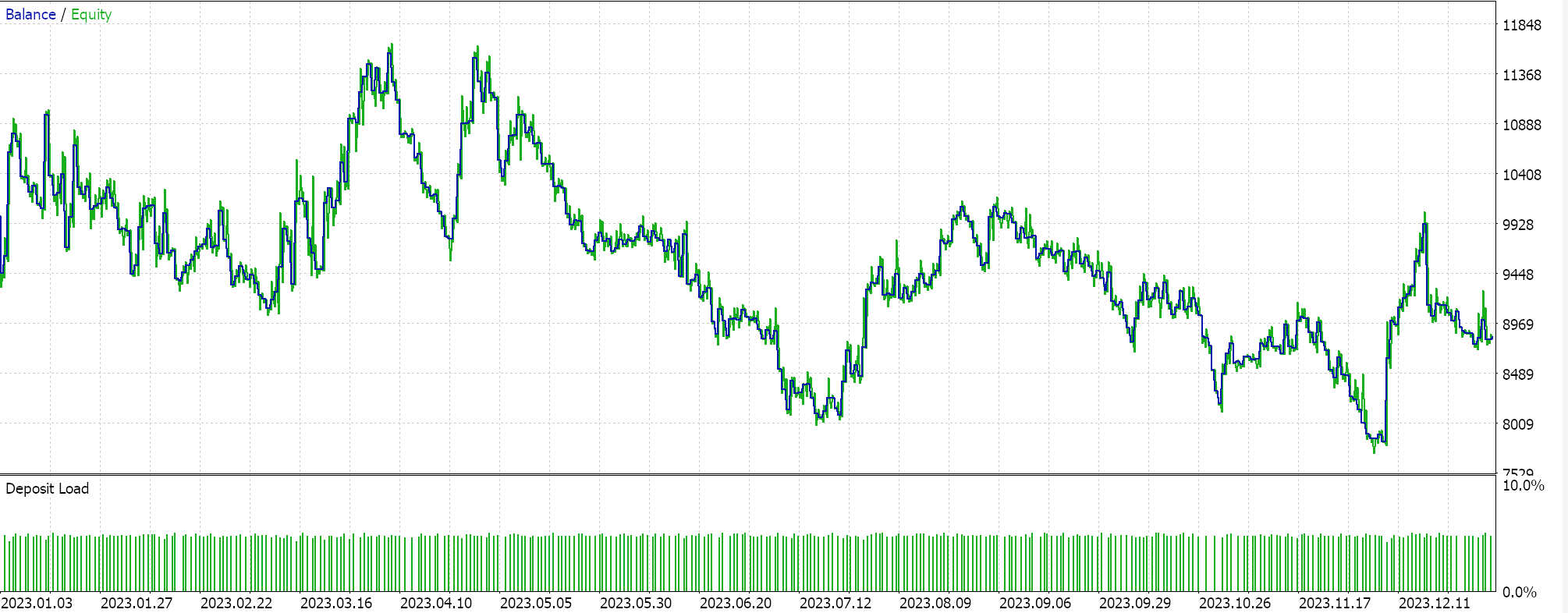
結果は、よく言えば物足りません。興味深いことに、コントロールとして、同じEAを移動平均ベースのトレール注文で実行すると、以下のレポートに示されているように、「より良い」結果が得られます。

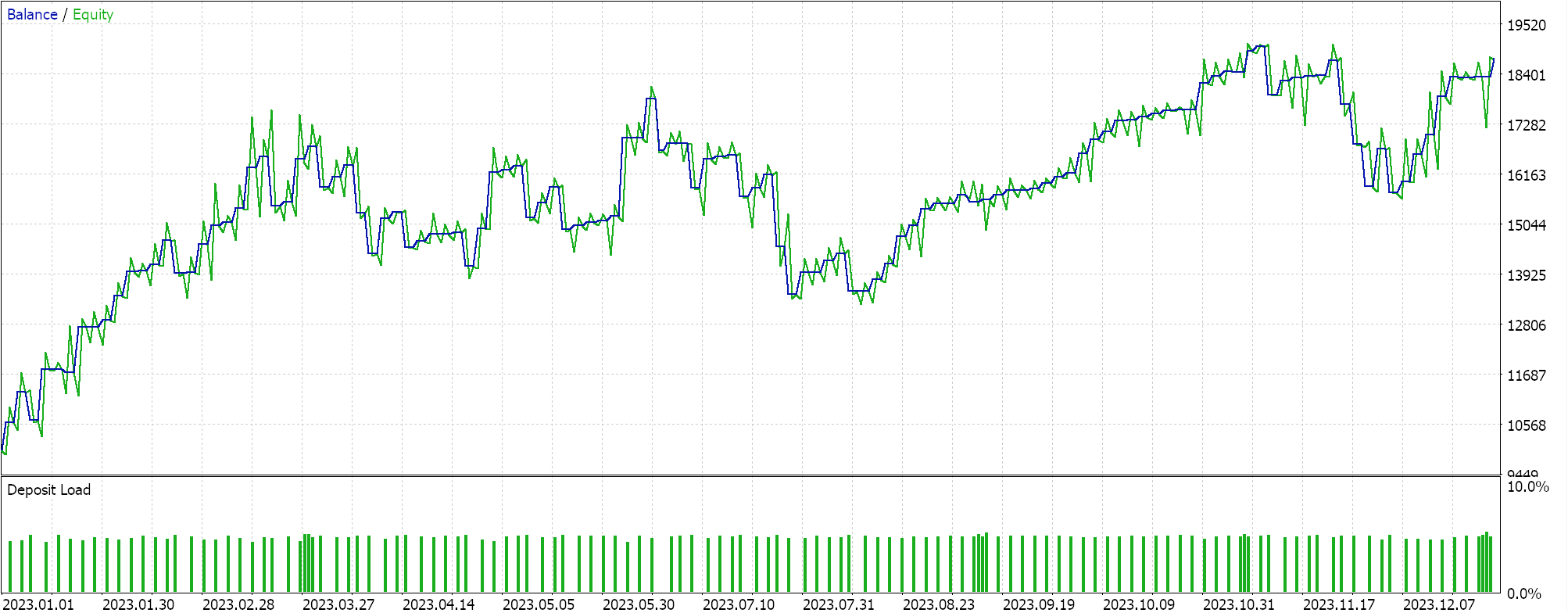
このような良い結果が得られたのは、多項式とは対照的に、より多くのパラメータが最適化されたからであり、実際、異なるEAのシグナルと組み合わせることで、根本的に異なる結果が得られる可能性があります。それにもかかわらず、対照実験目的では、これらの報告は、未決済ポジションの損切り管理におけるニュートン多項式の可能性についての指針として役立つでしょう。

マネーマネージメント

最後に、CExpertMoneyというラベルの付いた3番目のタイプの組み込みウィザードクラスによって処理されるポジションサイジングにニュートン多項式がどのように役立つかを検討します。さて、この多項式はどのように役立つのでしょうか。最適な使用方法を見つける方向性は確かにたくさんありますが、バー範囲の変化をボラティリティの指標、つまり固定マージンポジションサイズをどのように調整するかについてのガイドとして考慮します。ここでのシンプルなテーゼは、もし価格バーの範囲が上昇すると予想されるなら、それに比例してポジションサイズを縮小し、上昇しないなら何もしないというものです。予想されるボラティリティの低下による増加はありません。

これに役立つソースコードを以下に示します。上記で取り上げたものと同様の部分は省略しています。

//+------------------------------------------------------------------+
//| Optimizing lot size for open.                                    |
//+------------------------------------------------------------------+
double CMoneySizeOptimized::Optimize(double lots)
{  double lot = lots;
//--- 0 factor means no optimization
   if(m_decrease_factor > 0)
   {  m_high.Refresh(-1);
      m_low.Refresh(-1);
      vector _x, _y;
      _x.Init(m_length);
      _y.Init(m_length);
      for(int i = 0; i < m_length; i++)
      {  _x[i] = i;
         _y[i] = (m_high.GetData(StartIndex() + i) - m_low.GetData(StartIndex() + i)) - (m_high.GetData(StartIndex() + i + 1) - m_low.GetData(StartIndex() + i + 1));
      }
      vector _w;
      _w.Init(m_length);
      _w[0] = _y[0];
      __N.Set(_w, _x, _y);
      double _xx = -1.0;
      double _yy = 0.0;
      __N.Get(_w, _x, _xx, _yy);
      //---
      if(_yy > 0.0)
      {  double _range = (m_high.GetData(StartIndex()) - m_low.GetData(StartIndex()));
         _range += (m_decrease_factor*m_symbol.Point());
         _range += _yy;
         lot = NormalizeDouble(lot*(1.0-(_yy/_range)), 2);
      }
   }
//--- normalize and check limits

...

//---
   return(lot);
}

もう一度、同じ銘柄、同じ時間枠で、トレーリングEAと同じシグナルクラスを使用するEAで、多項式ルックバック期間のみの最適化を実行すると、次のようなレポートが得られます。

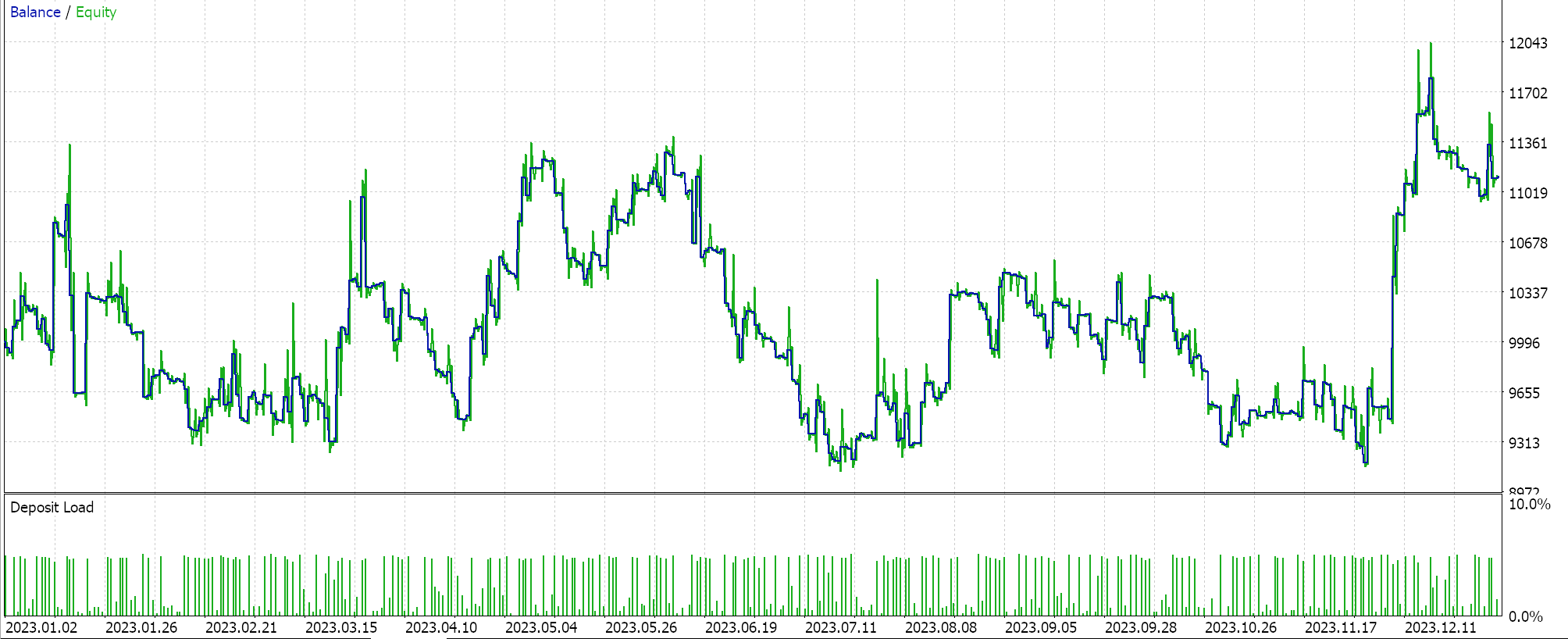
このEAでは、ウィザードでトレール注文の方法を選択しておらず、要するに、ボラティリティが予想される場合にポジションサイズを小さくすることで、変化のみをもたらすAwesome Oscillatorからの生のシグナルを使用しています。

コントロールとして、同様のシグナルとトレール注文なしのEAで、内蔵の「サイズ最適化」資金管理クラスを使用します。このEAでは、EAが被る損失に比例してポジションサイズを縮小する分数の分母を形成する減少要因のみを調整することができます。最適な設定でテストをおこなうと、以下のようなレポートが得られます。

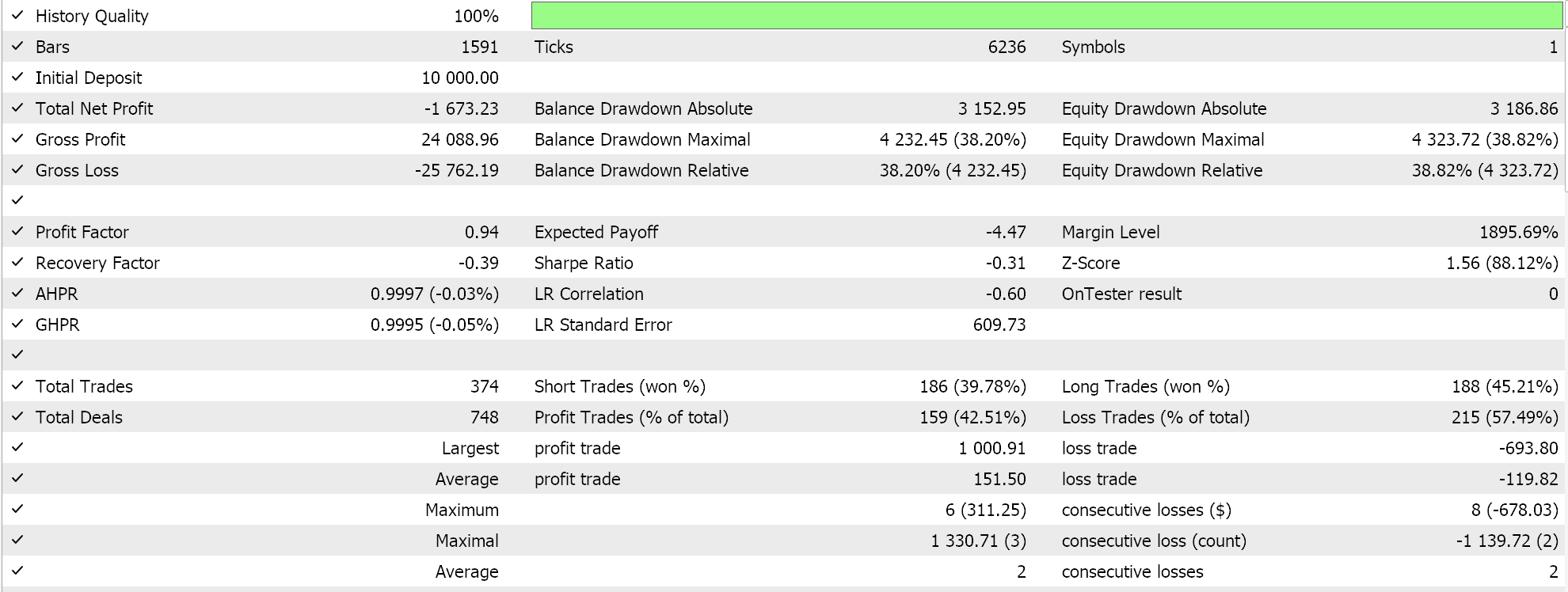
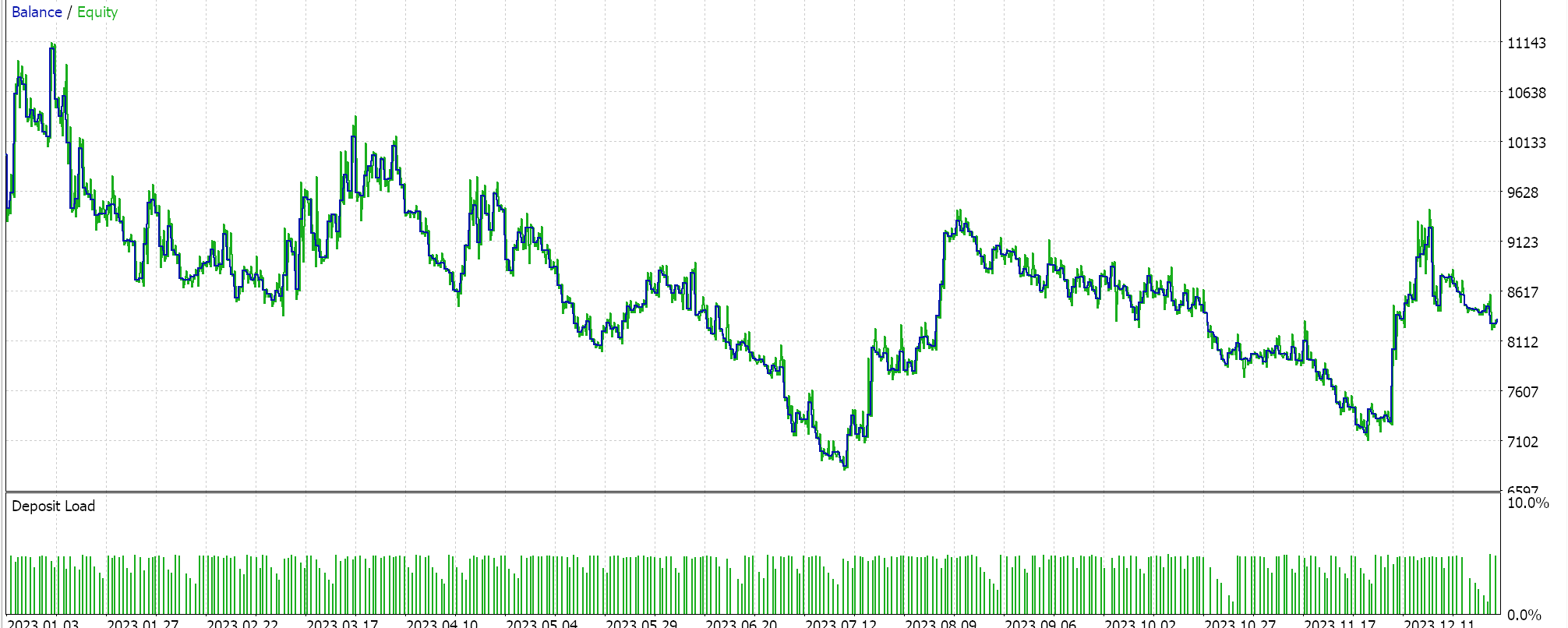
この結果は、ニュートン多項式資金管理で得たものと比べると、明らかに見劣りします。繰り返しますが、トレーリングクラスで見たように、ポジションサイズに最適化されたEAをそれ自体非難するものではありませんが、比較の目的としては、私たちが実装した方法でのニュートン多項式に基づいた資金管理がより良い代替手段であることを意味する可能性があります。

結論

ニュートン多項式、つまり数点のデータから多項式を導く方法を見てきました。この多項式、そして前回の記事で考察したナンバーウォール、あるいはその前の制限ボルツマンマシンは、本連載で考察した以上の方法で使用できるアイデアを紹介したものです。

市場を分析する際に実証済みの手法に固執する支持者がいるという新進気鋭の学派があります。これらの記事はそれ自体に反対しているわけではありませんが、BTCから株式、債券、そしてコモディティに至るまで、あらゆるものが相関関係にあるという状況において、これはシステミックな出来事の前兆なのでしょうか。お金が簡単に手に入る時代には、エッジを捨てるのは簡単です。よって、こうした連載は、未知の世界に足を踏み入れる際に必要な保険となるような、新しい、そしてしばしば愛されていないアプローチを支持する手段として考えることができます。

本題に戻れば、上記のテストレポートに示されているように、ニュートン多項式には制限があります。これは主にホワイトノイズをフィルタで除去できないことに起因しており、これは、対処する他の指標と組み合わせるとうまく機能する可能性があることを意味します。MQL5ウィザードでは、複数のシグナルを1つのEAにペアリングすることができるため、より良いEAシグナルを導き出すために1つ以上のフィルタを使用することができます。トレーリングクラスと資金管理モジュールはこれを許さないので、どのトレーリングクラスと資金管理クラスがシグナルで最もうまく機能するか、もっとテストする必要があります。

つまり、ホワイトノイズをフィルタリングできないのは、多項式が根本的なパターンを処理する代わりに、すべての動きを捕捉することによって、サンプリングされたデータに過剰適合する傾向があるためだと考えられます。これはしばしば「ノイズの記憶」と呼ばれ、サンプル外のデータではパフォーマンスの低下につながります。金融時系列は、統計的特性（平均、分散...）が変化し、価格の急激な変化が常態化する非線形ダイナミクスを持つ傾向があります。滑らかな多項式曲線に基づくニュートン多項式がこのような複雑さを捉えるのは困難です。最後に、景況感やファンダメンタルズを組み入れることができないということは、上記のように適切な金融指標と組み合わせる必要があるということです。