Affittuario - pagina 19

Nuovo commento
 

Sorento:

В чём другое? Ведь требуется строго больше. :)

Beh, Dio non voglia, rigorosamente così! Sono d'accordo.

 
Neutron:


Stimate con il vostro metodo e datemi il risultato.

Con le condizioni { N=120, q(mo)=60,91%/12 Capitale iniziale=100 } che ho dato nel grafico. e per armeggiare con K è fuori dalle mie mani.

Se qualcuno mi darà i kOpt per queste condizioni - farò una tabella postnumerand con gli arrotondamenti presi in considerazione...

;)

 

Quindi, ora una domanda per Matemat e Sorento: sopra, entrambi avete fatto riferimento alla decisione dell'unico Mikhail Andreyevich nel senso di - E adesso? tutto è chiaro... tipo - e poi?

Si scopre che lo stimato Mikhail Andreyevich non ha altro che una formula ridotta per il tempo di raddoppio del punteggio, niente:-) In generale, suppongo, aspettiamo una soluzione approssimativa per kOpt da Alexey.

 
Neutron:

Quindi, ora una domanda per Matemat e Sorento: sopra, entrambi avete fatto riferimento alla decisione dell'unico Mikhail Andreyevich nel senso di - E adesso? tutto è chiaro... tipo - e poi?

Si scopre che lo stimato Mikhail Andreyevich non ha altro che una formula ridotta per il tempo di raddoppio del punteggio, niente:-) Quindi, suppongo che aspettiamo una soluzione approssimativa per kOpt da Alexey.

Conclusione interessante.

Le strategie che implicano qualsiasi ritiro (anche proporzionale) prima della scadenza Topt - non sono ottimali... Supponendo che il depo sia più lungo del Topt - naturalmente.

Si prega di vedere le immagini (numeriche)...

;)

 

Sembra che stiamo iniziando a risolvere un problema leggermente diverso (più complicato).

Vi ricordo che per stipulazione, ho un deposito in uso per il tempo t, sul quale matura mensilmente un interesse costante q dell'importo corrente del deposito, e DEVO ritirare ogni mese un interesse fisso k, non superiore a q e non inferiore a 0%. Questo è tutto.

Devo trovare tale kOpt che massimizza il ritiro nel periodo t senza tener conto del deposito. Questa soluzione deve essere presentata in forma analitica come funzione di due parametri q e t (soluzioni numeriche, soluzioni parziali sotto forma di ogni sorta di grafici e dipendenze non sono di alcun interesse, perché sono già state ottenute). Se la soluzione analitica è approssimativa, allora bisogna specificare i limiti per q e t , in cui si raggiunge la precisione dichiarata della soluzione del problema.

P.S. Tutti gli espedienti come l'inflazione, la non costanza dell'interesse maturato q, le variazioni del parametro k, ecc. penso che non abbia senso considerare fino a quando non si ottiene la soluzione del caso più semplice.

 

"Ricordiamo che per convenzione, ho un deposito in uso per il tempo t, sul quale matura mensilmente una percentuale costante q dell'importo corrente del deposito, e DEVO ritirare ogni mese una percentuale fissa k non superiore a q e non inferiore a 0%. Questo è tutto".

.

Sergey, e c'è già una risposta alla domanda, anche se la formula non è troppo semplice, ma è abbastanza comprensibile. La risposta in questi casi è di solito data nei libri di riferimento sotto forma di nomogrammi.

Dalla specifica del problema possiamo vedere: "q si trova nell'intervallo 0,1<q<0,3".

Specificare anche l'intervallo "tempo t"

 

Oleg, per Forex t può essere impostato a 50. Meno non ha senso, perché con la vita caratteristica del deposito inferiore a 5 anni, è corretto ritirare tutti i profitti, e la dimensione iniziale del deposito dovrebbe fornire "a vita" sugli interessi. Se il tempo di vita più di 5 anni, allora la dimensione del deposito iniziale non è un problema e si può iniziare con 1000 rubli, ma non appare la percentuale di ritiro ottimale. Inoltre, se teniamo conto che il tempo di vita caratteristica non è obbligatorio per l'esecuzione (perché stiamo parlando di statistica), possiamo escludere questo parametro dalla formula mettendolo uguale a costante=50. Così, abbiamo (idealmente) per kOpt un valore di approssimazione analitica da un solo parametro - la competenza media di TC - q.

kOpt=q per t<50

kOpt=F(q) per t>50

La forma approssimata della dipendenza analitica F(q) nelle condizioni specificate è ciò che vogliamo scoprire.

 

Non so ancora come rendere la formula semplice. Il metodo di Newton dà una soluzione più o meno esatta almeno dalla terza o quarta iterazione. Risulta essere una formula molto ingombrante e a più livelli.

Il chiarimento di q ora conferma ulteriormente che l'espansione binomiale è inutile qui: anche a q=0,1 e t=10 si devono mantenere troppi termini del binomio. E più grandi sono t e q, peggio è. In altre parole, per t ragionevole (probabilmente non meno di 20) quasi sempre

(1+q-k)^t ~ exp((q-k)t)

Le osservazioni dicono che con q grande e t piccolo (diciamo 0,3 e 10, rispettivamente) è ottimale ritirare lamaggior parte di ciò che guadagno in un mese (70%).

Con q piccolo e t piccolo non c'è un estremo all'interno di un intervallo ragionevole: è necessario ritirare tutti i vostri guadagni.

Allo stesso tempo, con q medio e t medio (0,2 e 20) è ragionevole ritirare una parte sostanziale della metà dei propri guadagni (44%).

Poi, con q medio e t grande (0,2 e 30), è ragionevole ritirare una frazione minore dei vostri guadagni (26%).

E così via. Il problema si comporta qualitativamente in modo diverso sotto diversi parametri. Non sembra esserci una risposta unica e ottimista. Forse provare a fare una specie di stima di k in funzione di q e t?

P.S. Ho visto il tuo commento, Sergey. OK, fissare t=50. Il problema è diventato più facile: è sufficiente ritirare una parte minore dei guadagni(q=0,1, t=50-> k/q= 0,3, cioè il 30%). Questo è il massimo k/q possibile.

 

..................

.................

................

Il valore ottimale di alfa corrisponde alla transizione dalla regione positiva a quella negativa.

.

La formula è stata data sopra, la ripeterò qui

Potete riprodurlo in Matcadet --- potete regolare rapidamente i parametri.

(e B non gioca un ruolo).

 
Mathemat:

Forse provare a fare una specie di stima di k in funzione di q e t?


Allora si perde l'eleganza della soluzione analitica. In questo caso, è più corretto usare una soluzione numerica. Il problema sembra essere fuori portata per una semplice espressione...

Ho cercato di semplificare l'espressione originale per la somma dei prelievi .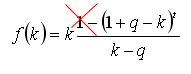

In questo caso, la forma generale della derivata prima sul parametro k è molto semplificata, fino a una semplice equazione quadratica:

.

Risolvendola, si può ottenere un'espressione approssimata per

Con una precisione accettabile nell'intervallo t>50, q>0.1

Volevo di più...

1...121314151617181920212223242526...31
Nuovo commento