Locataire - page 16
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Il est intéressant de voir comment ces paramètres affectent le résultat :
Par exemple, pour nos conditions de base, à différentes positions de la valve, nous obtenons ces images intéressantes
.
.
.
C'est pour la vue d'ensemble...
Nous nous intéressons à la dernière dépendance
(profil de phase "a-da" -- le dernier graphique en est un cas particulier)
Ça n'a pas très bien marché. Je ne publierai pas les calculs ici. Il n'y a rien de beau en eux.
J'ai essayé d'utiliser l'observation suivante : 1+q-k = 1+epsilon, epsilon étant une petite valeur. J'ai ensuite développé la dérivée par k en série de Taylor, en retenant d'abord les termes jusqu'au troisième ordre de petitesse. Puis, après des simplifications, nous avons obtenu l'équation cubique. J'ai éliminé le plus petit terme du troisième ordre et j'ai essayé de résoudre le quadratique résultant. J'ai échoué : le discriminant n'est positif que pour un petit t.
J'ai peur d'avoir fait une erreur en rejetant le terme cubique : bien qu'il s'agisse d'un terme du troisième ordre de petitesse en epsilon, il n'est pas petit. Je l'avais comme suit : epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3). On peut voir que pour un grand t, il peut être assez petit (même si epsilon~0.01 est une hypothèse assez réaliste). Et on ne veut pas résoudre le cubique.
Voyons ce qu'obtient Oleg.
P.S. En supposant que epsilon*t = O(1) (ou q*t = O(1) ), vous pouvez approximer la fonction puissance par un exposant. Faisons un essai.
Il existe une autre approche - sans série de Taylor, mais simplement par la méthode des tangentes (Newton, je crois). Et on peut aussi arriver à une solution analytique assez exacte.
Le fait est qu'au départ, les conditions ne contiennent pas un temps continu, mais une fonction de treillis -- c'est-à-dire qu'une transformation appropriée doit d'abord être effectuée. Ce n'est qu'alors que l'introduction d'un petit epsilon sera valable. Ce sont les propriétés des fonctions de treillis.
Au fait, c'est la translation vers la région de temps continu que j'ai traitée dans la première étape de la résolution du problème, en utilisant la transformée de Laplace dans la chaîne discrète--fréquences-temps. Pour être plus exact : également par ce...
Ainsi, l'objet de notre analyse ultérieure est la fonction
.
Et je ne veux pas résoudre le problème cubique.
Alexey, je n'ai jamais vu d'expression analytique pour les racines d'une équation cubique (sauf pour les cas simplifiés partiels). N'avez-vous pas une telle expression ? Tout comme pour une équation quadratique : x1=b/2+SQRT()... etc. Publiez-le si vous le connaissez. Je n'ai rien trouvé sur Internet. Je me souviens qu'à l'école, il existe même une représentation des racines par des fonctions harmoniques !
Il existe une autre approche - sans série de Taylor, mais simplement par la méthode des tangentes (Newton, je crois). Et on peut aussi arriver à une solution analytique assez exacte.
Est-il vraiment possible d'obtenir une solution approximative sous forme analytique de cette manière ? Jamais entendu parler. Très intéressant, j'aimerais voir un exemple de la méthode.
Allons au studio !
Oui, vous parlez de la solution obtenue pour un grand t. Cette situation présente également un intérêt pratique en tant que cas de dépôt "impossible à tuer". Pour quel t avez-vous réussi à obtenir une approximation ? Peut-être qu'une transition limite pour t->inf est possible. Nous pouvons alors obtenir une expression analytique du pourcentage optimal de paiement, k, en fonction d'un seul paramètre q - la valeur des intérêts courus. Ce serait un excellent résultat.
avtomat:
Le fait est que les conditions initiales ne contiennent pas un temps continu, mais une fonction de treillis -- c'est-à-dire qu'une conversion doit d'abord être effectuée. Ce n'est qu'alors que l'introduction d'un petit epsilon serait valable. Ce sont les propriétés des fonctions de treillis.
Au fait, c'est la translation vers la région de temps continu que j'ai traitée dans la première étape de la résolution du problème, en utilisant la transformée de Laplace dans la chaîne discrète--fréquences-temps. Pour être plus exact : y compris ceci...
Oleg, pourquoi pensez-vous que l'expression analytique obtenue ci-dessus pour la somme des moyennes dérivables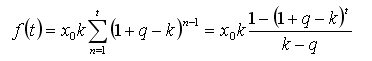
n'est pas marginale pour le temps continu ? Après tout, nous n'avons pas stipulé la limite minimale de l'intervalle (pas) de la série temporelle originale (forme itérative de l'écriture dans le premier post du sujet). Si oui, il suffit qu'à la transition limite à dt->0 on ait un certain df(t) et il n'y a pas de contradiction...
Oleg, pourquoi pensez-vous que l'expression analytique ci-dessus pour la somme des dérivées n'est pas la limite pour le temps continu ? Après tout, nous n'avons pas spécifiquement stipulé une restriction sur l'intervalle minimum (pas) de la série temporelle originale (forme itérée de la notation dans le premier post du sujet). Si c'est le cas, alors il suffit qu'à la transition limite à dt->0 nous ayons un df(t) défini et il n'y a pas de contradiction...
Pas si... Essayez d'introduire un petit epsilon ici...
Oui, nous ne l'avons stipulé nulle part, mais la formulation du problème lui-même implique implicitement l'utilisation d'une fonction de treillis.
Cela signifie que la correspondance se fera dans les nœuds du treillis. De plus, pour les fonctions de treillis, il n'y a pas de points intermédiaires - seulement les nœuds du treillis. Ainsi, toutes les tentatives de construction de valeurs intermédiaires conduiront à des résultats erronés (d'ailleurs, ces questions appartiennent au domaine de la quantification du signal). Les valeurs intermédiaires peuvent être construites en augmentant le taux d'échantillonnage, c'est-à-dire en introduisant à nouveau une fonction de treillis avec plus de nœuds, ce qui ne changera pas fondamentalement l'essence du phénomène. Cela signifie, en particulier, que des dérivées premières, secondes, etc. sont utilisées à la place des différences premières, secondes, etc. Au lieu d'intégrales, des sommes. . . etc. -- ... c'est tout un champ d'études.
Mais il existe des moyens de passer d'une zone à l'autre et de revenir.
Dans le cas particulier de notre problème, cette approche ne nous convient pas. La première chose à faire est donc de passer du temps discret au temps continu.
Le fait est que les conditions initiales ne sont pas en temps continu, mais une fonction de treillis - c'est-à-dire qu'une transformation doit d'abord être effectuée.
Je n'ai jamais vu d'expression analytique pour les racines d'une équation cubique (à l'exception des simplifications partielles). Vous n'en avez pas ? Tout comme pour une équation quadratique : x1=b/2+SQRT()... etc. Publiez-le si vous le connaissez. Je ne peux rien trouver sur Internet.
La formule de Cardano.
Je me souviens de l'école qu'il existe même une représentation des racines par des fonctions harmoniques !
La formule trigonométrique de Viets
... Ou encore de ne pas produire, mais d'utiliser l'appareil disponible de la version discrète de la transformée de Laplace, c'est-à-dire la transformation Z. Ne pensez-vous pas que ce serait plus simple ?
Ce n'est pas le problème. Au tout début, il y a une image tridimensionnelle de "%croissance - %rendement - rendement" - tout est déjà calculé, et c'est dans le domaine discret.
Maintenant, la tâche sportive est de présenter tout cela sous une forme analytique ;)
Formule Cardano
La formule trigonométrique de Vyet