Comment créer des graphiques 3D avec DirectX dans MetaTrader 5
Les infographies tridimensionnelles donnent l'impression d'objets tridimensionnels sur un écran plat. Ces objets, ainsi que la position du spectateur, peuvent changer au fil du temps. Par conséquent, l'image bidimensionnelle doit également changer pour créer l'illusion de la profondeur de l'image. Elle doit supporter la rotation, le zoom, les changements d'éclairage, etc. MQL5 permet de créer et de gérer des graphiques directement dans le terminal MetaTrader 5 en utilisant les fonctions DirectX. Veuillez noter que votre carte vidéo doit prendre en charge DirectX 11 et Shader Model 5.0 pour que les fonctions fonctionnent.
- Modélisation d'Objets
- Création d’une Forme
- Calcul et Rendu d’une Scène
- Rotation d’un Objet autour de l'Axe Z et Point de Vue
- Gestion de la Position de la Caméra
- Gestion de la Couleur des Objets
- Rotation et Mouvement
- Travailler avec l’Éclairage
- Animation
- Contrôle de la Position de la Caméra à l'aide de la Souris
- Application des Textures
- Création d’Objets Personnalisés
- Surface 3D Basée sur des Données
Modélisation d'Objets
Pour dessiner un objet 3D sur un plan (espace plat), il faut d'abord obtenir un modèle de cet objet en coordonnées X, Y et Z. Cela signifie que chaque point de la surface de l'objet doit être décrit en spécifiant ses coordonnées. Idéalement, il faudrait décrire un nombre infini de points sur la surface de l'objet pour préserver la qualité de l'image pendant la mise à l'échelle. Dans la pratique, les modèles 3D sont décrits à l'aide d'un maillage composé de polygones. Plus un maillage est détaillé avec un nombre élevé de polygones, plus le modèle obtenu sera réaliste. Par contre, il faut également plus de ressources informatiques pour calculer un tel modèle et faire le rendu des graphiques 3D.
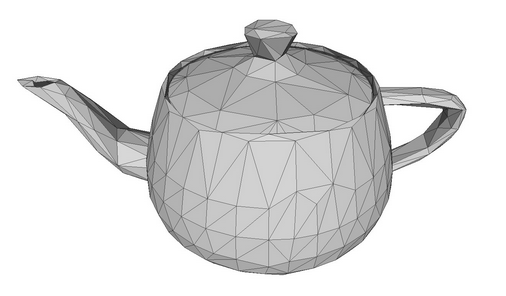
Un modèle de théière avec un maillage polygonal.
La division des polygones en triangles est apparue il y a longtemps, lorsque les premières images de synthèse devaient fonctionner sur des cartes graphiques peu performantes. Le triangle permet de décrire exactement de la position d'une petite partie de surface. Il permet aussi le calcul des paramètres associés, tels que les lumières et les réflexions lumineuses. L’ensemble de ces petits triangles permet de créer une image tridimensionnelle réaliste de l'objet. Par la suite, les mots ’polygone’ et ’triangle’ seront utilisés indifféremment car il est beaucoup plus facile d'imaginer un triangle qu'un polygone avec N sommets.
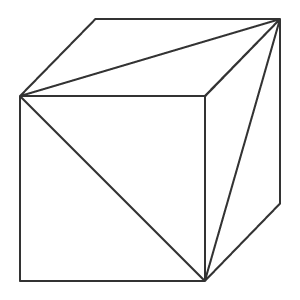
Cube constitué de triangles
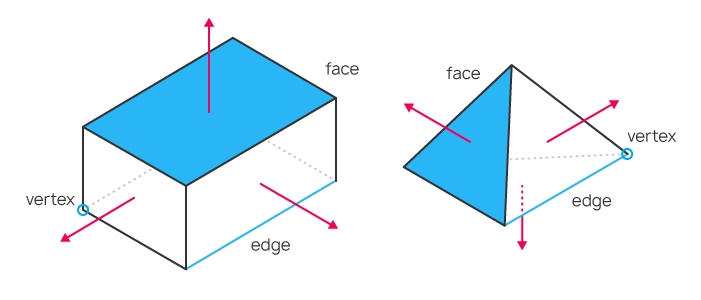
Il est possible de créer le modèle tridimensionnel d'un objet en décrivant les coordonnées de chaque sommet du triangle, ce qui permet ensuite le calcul des coordonnées de chaque point de l'objet, même si l'objet se déplace ou si la position de l'observateur change. Nous traitons donc des sommets, des arêtes qui les relient, et des faces formées par les arêtes. Si la position d'un triangle est connue, nous pouvons créer une normale pour la face en utilisant les lois de l'algèbre linéaire (une normale est un vecteur perpendiculaire à la surface). Elle permet de calculer la façon dont sera éclairée le visage et il réfléchira la lumière.
Exemples d'objets simples avec leurs sommets, arêtes, faces et normales. Les normales sont représentées par une flèche rouge.
Un objet modèle peut être créé de différentes manières. La topologie décrit comment les polygones forment le maillage 3D. Une bonne topologie permet d'utiliser un nombre minimal de polygones pour décrire un objet et peut faciliter le déplacement et la rotation de l'objet.
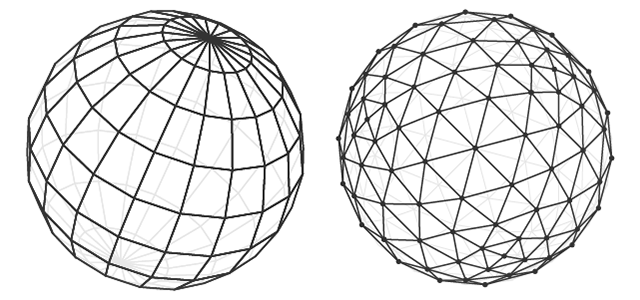
Modèle de sphère dans 2 topologies
L'effet de volume est recréé en utilisant des lumières et des ombres sur les polygones de l'objet. Ainsi, le but de l'infographie 3D est de calculer la position de chaque point d'un objet, de calculer les lumières et les ombres et de l'afficher à l'écran.
Création d’une Forme
Écrivons un programme simple qui va créer un cube. Pour cela, utilisons la classe CCanvas3D de la bibliothèque Graphiques 3D.
La classe CCanvas3DWindow, qui effectue le rendu d'une fenêtre 3D, possède un minimum de membres et de méthodes. Nous ajouterons progressivement de nouvelles méthodes avec une explication des concepts graphiques 3D mis en œuvre dans des fonctions permettant de travailler avec DirectX.
//+------------------------------------------------------------------+ //| Application window | //+------------------------------------------------------------------+ class CCanvas3DWindow { protected: CCanvas3D m_canvas; //--- canvas size int m_width; int m_height; //--- the Cube object CDXBox m_box; public: CCanvas3DWindow(void) {} ~CCanvas3DWindow(void) {m_box.Shutdown();} //-- create a scene virtual bool Create(const int width,const int height){} //--- calculate the scene void Redraw(){} //--- handle chart events void OnChartChange(void) {} };
La création d'une scène commence par la création d'un canevas. Les paramètres suivants sont ensuite définis pour la matrice de projection :
- Un angle de vue de 30 degrés (M_PI/6), à partir duquel nous observerons la scène en 3D
- Le rapport d'aspect, qui est un rapport entre la largeur et la hauteur
- Les distances au plan de coupe proche (0.1f) et éloigné (100.f)
Cela signifie que seul le rendu des objets situés entre ces deux murs virtuels (0.1f et 100.f) sera effectué dans la matrice de projection. En outre, les objets doivent se trouver dans l'angle de vue horizontal de 30 degrés. Et notez également que les distances ainsi que toutes les coordonnées en infographie sont virtuelles. Ce qui importe, ce sont les relations entre les distances et les tailles, et pas les valeurs absolues.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { //--- save canvas dimensions m_width=width; m_height=height; //--- create a canvas to render a 3D scene ResetLastError(); if(!m_canvas.CreateBitmapLabel("3D Sample_1",0,0,m_width,m_height,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return(false); } //--- set projection matrix parameters - angle of view, aspect ratio, distance to the near and far clip planes m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- create cube - pass to it the resource manager, scene parameters and coordinates of two opposite corners of the cube if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,5.0),DXVector3(1.0,1.0,7.0))) { m_canvas.Destroy(); return(false); } //--- add the cube to the scene m_canvas.ObjectAdd(&m_box); //--- redraw the scene Redraw(); //--- succeed return(true); }
Après avoir créé la matrice de projection, nous pouvons procéder à la construction de l'objet 3D : un cube basé sur la classe CDXBox. Pour créer un cube, il suffit d'indiquer 2 vecteurs pointant vers les coins opposés du cube. En observant la création du cube en mode débogage, vous pouvez voir ce qui se passe dans DXComputeBox() : la création de tous les sommets du cube (leurs coordonnées sont écrites dans le tableau 'vertices'), ainsi que la division des arêtes du cube en triangles énumérés et enregistrés dans le tableau 'indiсes'. Au total, le cube a 8 sommets, 6 faces divisées en 12 triangles, et 36 indices listant les sommets de ces triangles.
Bien que le cube n'ait que 8 sommets, 24 vecteurs sont créés pour les décrire, car un ensemble distinct de sommets ayant une normale doit être spécifié pour chacune des 6 faces. La direction de la normale affectera le calcul de l'éclairage de chaque face. L'ordre dans lequel les sommets d'un triangle sont listés détermine quel côté sera visible. L'ordre dans lequel les sommets et les indices sont remplis est montré dans le code de DXUtils.mqh :
for(int i=20; i<24; i++) vertices[i].normal=DXVector4(0.0,-1.0,0.0,0.0);
Les coordonnées de la texture pour le mapping de chaque face sont décrites dans le même code :
//--- texture coordinates for(int i=0; i<faces; i++) { vertices[i*4+0].tcoord=DXVector2(0.0f,0.0f); vertices[i*4+1].tcoord=DXVector2(1.0f,0.0f); vertices[i*4+2].tcoord=DXVector2(1.0f,1.0f); vertices[i*4+3].tcoord=DXVector2(0.0f,1.0f); }
Chacun des 4 vecteurs d’une face définit l'un des 4 angles pour le mapping de la texture. Cela signifie qu'un ensemble de structures sera mappé sur chaque face du cube pour faire le rendu de la texture. Cela n'est par contre nécessaire que si la texture est définie.
Calcul et Rendu d’une Scène
Tous les calculs doivent être recalculés à chaque fois que la scène 3D est modifiée. Voici l'ordre des calculs nécessaires :
- Calcul du centre de chaque objet en coordonnées mondiales
- Calcul de la position de chaque élément de l'objet, c'est-à-dire de chaque vertex
- Calcul de la profondeur des pixels et de leur visibilité pour l'observateur
- Calcul de la position de chaque pixel sur le polygone spécifié par ses sommets.
- Définition de la couleur de chaque pixel sur le polygone en fonction de la texture spécifiée
- Calcul de la direction du pixel lumineux et de sa réflexion
- Application d’une lumière diffuse à chaque pixel
- Conversion de toutes les coordonnées du monde en coordonnées de la caméra
- Conversion des coordonnées de la caméra en coordonnées sur la matrice de projection
//+------------------------------------------------------------------+ //| Update the scene | //+------------------------------------------------------------------+ void Redraw() { //--- calculate the 3D scene m_canvas.Render(DX_CLEAR_COLOR|DX_CLEAR_DEPTH,ColorToARGB(clrBlack)); //--- update the picture on the canvas in accordance with the current scene m_canvas.Update(); }
Dans notre exemple, le cube est créé une seule fois, et il ne change plus. Par conséquent, le cadre du canevas ne devra être modifié que si le graphique est modifié, par exemple s'il est redimensionné. Dans ce cas, les dimensions du canevas sont ajustées aux dimensions actuelles du graphique, la matrice de projection est réinitialisée et l’image sur le canevas est mise à jour.
//+------------------------------------------------------------------+ //| Process chart change event | //+------------------------------------------------------------------+ void OnChartChange(void) { //--- get current chart sizes int w=(int)ChartGetInteger(0,CHART_WIDTH_IN_PIXELS); int h=(int)ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS); //--- update canvas dimensions in accordance with the chart size if(w!=m_width || h!=m_height) { m_width =w; m_height=h; //--- resize canvas m_canvas.Resize(w,h); DXContextSetSize(m_canvas.DXContext(),w,h); //--- update projection matrix in accordance with the canvas sizes m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- recalculate 3D scene and render it onto the canvas Redraw(); } }
Lancez l'EA "Step1 Create Box.mq5". Vous verrez un carré blanc sur un fond noir. Par défaut, la couleur blanche est définie pour les objets lors de leur création. L'éclairage n'a pas encore été défini.
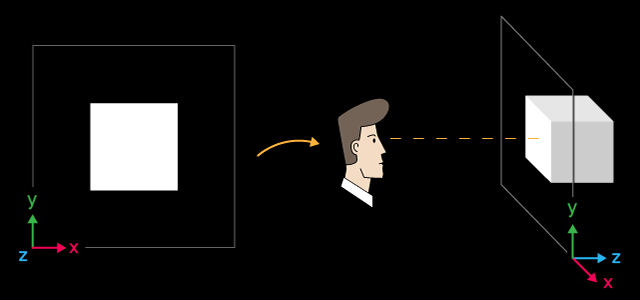
Un cube blanc et sa disposition dans l'espace
L'axe X est dirigé vers la droite, l’axe Y est dirigé vers le haut et l’axe Z est dirigé vers l'intérieur de la scène 3D. Un tel système de coordonnées est appelé gaucher.
Le centre du cube se trouve au point de coordonnées X=0, Y=0, Z=6. La position à partir de laquelle nous regardons le cube est au centre des coordonnées, ce qui est la valeur par défaut. Si vous souhaitez modifier la position à partir de laquelle la scène 3D est visualisée, définissez explicitement les coordonnées appropriées à l'aide de la fonction ViewPositionSet().
Pour stopper le programme, appuyez sur la touche "Echap".
Rotation d’un Objet autour de l'Axe Z et Point de Vue
Pour animer la scène, activons la rotation du cube autour de l'axe Z. Pour ce faire, ajoutez une minuterie. En fonction de ses événements, le cube sera tourné dans le sens inverse des aiguilles d'une montre.
Créez une matrice de rotation pour permettre la rotation autour de l'axe Z avec un angle donné en utilisant la méthode DXMatrixRotationZ(). Passez-le ensuite comme paramètre à la méthode TransformMatrixSet(). Cela modifiera la position du cube dans l'espace 3D. Appelez de nouveau Redraw() pour mettre à jour l'image sur le canevas.
//+------------------------------------------------------------------+ //| Timer handler | //+------------------------------------------------------------------+ void OnTimer(void) { //--- variables for calculating the rotation angle static ulong last_time=0; static float angle=0; //--- get the current time ulong current_time=GetMicrosecondCount(); //--- calculate the delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- increase the angle of rotation of the cube around the Z axis angle+=deltatime; //--- remember the time last_time=current_time; //--- set the angle of rotation of the cube around the Z axis DXMatrix rotation; DXMatrixRotationZ(rotation,angle); m_box.TransformMatrixSet(rotation); //--- recalculate 3D scene and render it onto the canvas Redraw(); }
Après avoir lancé le programme, vous verrez un carré blanc en rotation.

Le cube tourne autour de l'axe Z dans le sens inverse des aiguilles d'une montre.
Le code source de cet exemple est disponible dans le fichier "Step2 Rotation Z.mq5". Veuillez noter que l'angle M_PI/5 est spécifié maintenant lors de la création de la scène, ce qui est supérieur à l'angle M_PI/6 de l'exemple précédent.
//--- set projection matrix parameters - angle of view, aspect ratio, distance to the near and far clip planes m_matrix_view_angle=(float)M_PI/5; m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- create cube - pass to it the resource manager, scene parameters and coordinates of two opposite corners of the cube
La dimension du cube à l'écran est visuellement plus petite. Plus l'angle de vue spécifié lors du réglage de la matrice de projection est petit, plus la partie du cadre occupée par l'objet est grande. Cela peut être comparé à voir un objet avec un télescope : l'objet est plus grand, bien que l'angle de vue soit plus petit.
Gestion de la Position de la Caméra
La classe CCanvas3D dispose de 3 méthodes pour définir les paramètres importants de la scène 3D :
- ViewPositionSet définit le point de vue de la scène 3D
- ViewTargetSet définit les coordonnées du point d'observation
- ViewUpDirectionSet définit la direction du bord supérieur du cadre dans l'espace 3D
Tous ces paramètres sont utilisés en combinaison. Ce qui signifie que si vous voulez définir l'un de ces paramètres dans la scène 3D, les deux autres paramètres doivent également être initialisés. Cela devrait être fait au moins à l'étape de la génération de la scène. Ceci est illustré dans l'exemple suivant, dans lequel le bord supérieur du cadre oscille de gauche à droite. L’oscillation est implémentée en ajoutant les trois lignes de code suivantes dans la méthode Create() :
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { .... //--- add the cube to the scene m_canvas.ObjectAdd(&m_box); //--- set the scene parameters m_canvas.ViewUpDirectionSet(DXVector3(0,1,0)); // set the direction vector up, along the Y axis m_canvas.ViewPositionSet(DXVector3(0,0,0)); // set the viewpoint from the center of coordinates m_canvas.ViewTargetSet(DXVector3(0,0,6)); // set the gaze point at center of the cube //--- redraw the scene Redraw(); //--- succeed return(true); }
Modifiez la méthode OnTimer() pour que le vecteur horizon oscille de gauche à droite :
//+------------------------------------------------------------------+ //| Timer handler | //+------------------------------------------------------------------+ void OnTimer(void) { //--- variables for calculating the rotation angle static ulong last_time=0; static float max_angle=(float)M_PI/30; static float time=0; //--- get the current time ulong current_time=GetMicrosecondCount(); //--- calculate the delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- increase the angle of rotation of the cube around the Z axis time+=deltatime; //--- remember the time last_time=current_time; //--- set the rotation angle around the Z axis DXVector3 direction=DXVector3(0,1,0); // initial direction of the top DXMatrix rotation; // rotation vector //--- calculate the rotation matrix DXMatrixRotationZ(rotation,float(MathSin(time)*max_angle)); DXVec3TransformCoord(direction,direction,rotation); m_canvas.ViewUpDirectionSet(direction); // set the new direction of the top //--- recalculate 3D scene and render it onto the canvas Redraw(); }
Enregistrez cet exemple sous le nom de "Step3 ViewUpDirectionSet.mq5" et exécutez-le. Vous verrez l'image d'un cube qui se balance, bien qu'il soit en réalité immobile. Cet effet est obtenu lorsque la caméra elle-même oscille de gauche à droite.

La direction de la partie supérieure oscille entre la gauche et la droite.
Gestion de la Couleur des Objets
Modifions notre code pour placer le cube au centre des coordonnées, tout en déplaçant la caméra.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... //--- create cube - pass to it the resource manager, scene parameters and coordinates of two opposite corners of the cube if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- set the color m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- add the cube to the scene m_canvas.ObjectAdd(&m_box); //--- set positions for camera, gaze and direction of the top m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); // set the direction vector up, along the Y axis m_canvas.ViewPositionSet(DXVector3(3.0,2.0,-5.0)); // set camera on the right, on top and in front of the cube m_canvas.ViewTargetSet(DXVector3(0,0,0)); // set the gaze direction at center of the cube //--- redraw the scene Redraw(); //--- succeed return(true); }
Et peignons aussi le cube en bleu. La couleur est définie au format RGB avec un canal alpha (le canal alpha est indiqué en dernier), bien que les valeurs soient normalisées à un. Une valeur de 1 signifie donc 255, et 0,5 signifie 127.
Ajoutez la rotation autour de l'axe X, puis enregistrez les modifications sous le nom de "Step4 Box Color.mq5".

Vue supérieure droite d'un cube en rotation
Rotation et Mouvement
Les objets peuvent être déplacés et tournés dans les 3 directions à la fois. Tous les changements d'objets sont effectués à l'aide de matrices. Chacun de ces changements, c'est-à-dire la rotation, le déplacement et la transformation, peut être calculé séparément. Changeons notre exemple : la caméra est maintenant vue du haut et de l'avant.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- position the camera in top and in front of the center of coordinates m_canvas.ViewPositionSet(DXVector3(0.0,2.0,-5.0)); m_canvas.ViewTargetSet(DXVector3(0.0,0.0,0.0)); m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); //--- create cube - pass to it the resource manager, scene parameters and coordinates of two opposite corners of the cube if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- set the cube color m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- calculate the cube position and the transfer matrix DXMatrix rotation,translation; //--- rotate the cube sequentially along the X, Y and Z axes DXMatrixRotationYawPitchRoll(rotation,(float)M_PI/4,(float)M_PI/3,(float)M_PI/6); //-- move the cube to the right/downward/inward DXMatrixTranslation(translation,1.0,-2.0,5.0); //--- get the transformation matrix as a product of rotation and transfer DXMatrix transform; DXMatrixMultiply(transform,rotation,translation); //--- set the transformation matrix m_box.TransformMatrixSet(transform); //--- add the cube to the scene m_canvas.ObjectAdd(&m_box); //--- redraw the scene Redraw(); //--- succeed return(true); }
Créez séquentiellement des matrices de rotation et de déplacement, appliquez la matrice de transformation résultante et effectuez le rendu du cube. Enregistrez les changements dans le fichier "Step5 Translation.mq5" et exécutez le programme.

Rotation et déplacement d'un cube
La caméra est immobile, et elle est pointée vers le centre des coordonnées légèrement par le haut. Le cube a été tourné dans 3 directions et a été déplacé vers la droite, le bas et l'intérieur de la scène.
Travailler avec l’Éclairage
Pour obtenir une image tridimensionnelle réaliste, il est nécessaire de calculer l'éclairage de chaque point de la surface de l'objet. Ceci est fait en utilisant le modèle d'ombrage de Phong qui calcule l'intensité de la couleur des trois composantes d'éclairage suivantes : ambiante, diffuse et spéculaire. Les paramètres suivants sont utilisés ici :
- DirectionLight — la direction de l'éclairage directionnel est définie dans CCanvas3D
- AmbientLight — la couleur et l'intensité de l'éclairage ambiant sont définies dans CCanvas3D
- DiffuseColor — la composante d'éclairage diffus calculée est définie dans CDXMesh et ses classes filles.
- EmissionColor — le composant de l'éclairage de fond est défini dans CDXMesh et ses classes filles.
- SpecularColor — la composante spéculaire est définie dans CDXMesh et ses classes filles.

Modèle d'ombrage de Phong
Le modèle d'éclairage est implémenté dans des shaders standard, les paramètres du modèle sont définis dans CCanvas3D, et les paramètres des objets sont définis dans CDXMesh et ses classes filles. Modifions l'exemple comme suit :
- Renvoi du cube au centre des coordonnées.
- Réglage du cube sur blanc.
- Ajout d’une source directionnelle de couleur jaune qui illumine la scène du haut vers le bas.
- Définition de la couleur bleue pour l'éclairage non directionnel.
//--- set yellow color for the source and direct it from above downwards m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- set the blue color for the ambient light m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); //--- create cube - pass to it the resource manager, scene parameters and coordinates of two opposite corners of the cube if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- set the white color for the cube m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); //--- add green glow for the cube (emission) m_box.EmissionColorSet(DXColor(0.0,1.0,0.0,0.2f));
Veuillez noter que la position de la source lumineuse dirigée n'est pas définie dans Canvas3D, seule la direction dans laquelle la lumière se répand est donnée. On considère que la source de la lumière directionnelle est à une distance infinie et qu'un flux lumineux strictement parallèle illumine la scène.
m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); Ici, le vecteur de propagation de la lumière est dirigé le long de l'axe Y, dans la direction négative, c'est-à-dire du haut vers le bas. De plus, si vous définissez les paramètres de la source de lumière dirigée (LightColorSet et LightDirectionSet), vous devez également spécifier la couleur de la lumière ambiante (AmbientColorSet). Par défaut, la couleur de la lumière ambiante est définie sur blanc avec une intensité maximale. Toutes les ombres seront donc blanches. Cela signifie que les objets de la scène seront éclairés par la lumière blanche de l'éclairage ambiant, et que la lumière de la source directionnelle sera interrompue par la lumière blanche.
//--- set yellow color for the source and direct it from above downwards m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- set the blue color for the ambient light m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); // must be specified
L'animation gif ci-dessous montre comment l'image change si nous ajoutons un éclairage. Le code source de l'exemple est disponible dans le fichier "Step6 Add Light.mq5".

Le cube blanc à émission verte sous une source de lumière jaune, avec une lumière ambiante bleue
Essayez de désactiver les méthodes de couleur dans le code ci-dessus pour voir l’impact.
Animation
L'animation implique une modification des paramètres de la scène et des objets dans le temps. Toutes les propriétés disponibles peuvent être modifiées en fonction du temps ou des événements. Réglez le minuteur pour 10 millisecondes - cet événement affectera la mise à jour de la scène :
int OnInit() { ... //--- create canvas ExtAppWindow=new CCanvas3DWindow(); if(!ExtAppWindow.Create(width,height)) return(INIT_FAILED); //--- set timer EventSetMillisecondTimer(10); //--- return(INIT_SUCCEEDED); }
Ajoutez le gestionnaire d'événements correspondant dans CCanvas3DWindow. Nous devons modifier les paramètres des objets (tels que la rotation, le déplacement et le zoom) et la direction de l'éclairage :
//+------------------------------------------------------------------+ //| Timer handler | //+------------------------------------------------------------------+ void OnTimer(void) { static ulong last_time=0; static float time=0; //--- get the current time ulong current_time=GetMicrosecondCount(); //--- calculate the delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- increase the elapsed time value time+=deltatime; //--- remember the time last_time=current_time; //--- calculate the cube position and the rotation matrix DXMatrix rotation,translation,scale; DXMatrixRotationYawPitchRoll(rotation,time/11.0f,time/7.0f,time/5.0f); DXMatrixTranslation(translation,(float)sin(time/3),0.0,0.0); //--- calculate the cube compression/extension along the axes DXMatrixScaling(scale,1.0f+0.5f*(float)sin(time/1.3f),1.0f+0.5f*(float)sin(time/1.7f),1.0f+0.5f*(float)sin(time/1.9f)); //--- multiply the matrices to obtain the final transformation DXMatrix transform; DXMatrixMultiply(transform,scale,rotation); DXMatrixMultiply(transform,transform,translation); //--- set the transformation matrix m_box.TransformMatrixSet(transform); //--- calculate the rotation of the light source around the Z axis DXMatrixRotationZ(rotation,deltatime); DXVector3 light_direction; //--- get the current direction of the light source m_canvas.LightDirectionGet(light_direction); //--- calculate the new direction of the light source and set it DXVec3TransformCoord(light_direction,light_direction,rotation); m_canvas.LightDirectionSet(light_direction); //--- recalculate the 3D scene and draw it in the canvas Redraw(); }
Veuillez noter que les changements des objets sont appliqués sur les valeurs initiales, comme si nous traitions toujours avec l'état initial du cube et que nous appliquions toutes les opérations liées à la rotation/déplacement/compression à partir de zéro, ce qui signifie que l'état actuel du cube n'est pas sauvegardé. Cependant, la direction de la source lumineuse est modifiée par incréments de deltatime par rapport à la valeur actuelle.

Un cube en rotation dont la direction de la source lumineuse change dynamiquement
Le résultat est une animation 3D très complexe. Le code de l’exemple est disponible dans le fichier "Step7 Animation.mq5".
Contrôle de la Position de la Caméra à l'aide de la Souris
Considérons le dernier élément d'animation dans les graphiques 3D : une réaction aux actions de l'utilisateur. Ajoutons la gestion de la caméra avec la souris dans notre exemple. Tout d'abord, souscrivez aux événements de la souris et créez les gestionnaires correspondants :
int OnInit() { ... //--- set the timer EventSetMillisecondTimer(10); //--- enable receiving of mouse events: moving and button clicks ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,1); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,1) //--- return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { //--- Deleting the timer EventKillTimer(); //--- disable the receiving of mouse events ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,0); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,0); //--- delete the object delete ExtAppWindow; //--- return chart to the usual display mode with price charts ChartSetInteger(0,CHART_SHOW,true); } void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam) { ... //--- chart change event if(id==CHARTEVENT_CHART_CHANGE) ExtAppWindow.OnChartChange(); //--- mouse movement event if(id==CHARTEVENT_MOUSE_MOVE) ExtAppWindow.OnMouseMove((int)lparam,(int)dparam,(uint)sparam); //--- mouse wheel scroll event if(id==CHARTEVENT_MOUSE_WHEEL) ExtAppWindow.OnMouseWheel(dparam);
Dans CCanvas3DWindow, créez le gestionnaire d'événement du mouvement de la souris. Il change les angles de direction de la caméra lorsque la souris est déplacée avec le bouton gauche enfoncé :
//+------------------------------------------------------------------+ //| Handle mouse movements | //+------------------------------------------------------------------+ void OnMouseMove(int x,int y,uint flags) { //--- left mouse button if((flags&1)==1) { //--- there is no information about the previous mouse position if(m_mouse_x!=-1) { //--- update the camera angle upon change of position m_camera_angles.y+=(x-m_mouse_x)/300.0f; m_camera_angles.x+=(y-m_mouse_y)/300.0f; //--- set the vertical angle in the range between (-Pi/2,Pi2) if(m_camera_angles.x<-DX_PI*0.49f) m_camera_angles.x=-DX_PI*0.49f; if(m_camera_angles.x>DX_PI*0.49f) m_camera_angles.x=DX_PI*0.49f; //--- update camera position UpdateCameraPosition(); } //--- save mouse position m_mouse_x=x; m_mouse_y=y; } else { //--- reset the saved position if the left mouse button is not pressed m_mouse_x=-1; m_mouse_y=-1; } }
Voici le gestionnaire d'événement de la molette de la souris, qui modifie la distance entre le centre de la scène et la caméra :
//+------------------------------------------------------------------+ //| Handling mouse wheel events | //+------------------------------------------------------------------+ void OnMouseWheel(double delta) { //--- update the distance between the camera and the center upon a mouse scroll m_camera_distance*=1.0-delta*0.001; //--- set the distance in the range between [3,50] if(m_camera_distance>50.0) m_camera_distance=50.0; if(m_camera_distance<3.0) m_camera_distance=3.0; //--- update camera position UpdateCameraPosition(); }
Les deux gestionnaires appellent la méthode UpdateCameraPosition() pour actualiser la position de la caméra en fonction des paramètres modifiés :
//+------------------------------------------------------------------+ //| Updates the camera position | //+------------------------------------------------------------------+ void UpdateCameraPosition(void) { //--- the position of the camera taking into account the distance to the center of coordinates DXVector4 camera=DXVector4(0.0f,0.0f,-(float)m_camera_distance,1.0f); //--- camera rotation around the X axis DXMatrix rotation; DXMatrixRotationX(rotation,m_camera_angles.x); DXVec4Transform(camera,camera,rotation); //--- camera rotation around the Y axis DXMatrixRotationY(rotation,m_camera_angles.y); DXVec4Transform(camera,camera,rotation); //--- set camera to position m_canvas.ViewPositionSet(DXVector3(camera)); }
Le code source est disponible dans le fichier "Step8 Mouse Control.mq5".

Contrôle de la position de la caméra à l'aide de la souris
Application des Textures
Une texture est une image bitmap appliquée à la surface d'un polygone pour représenter des motifs ou des matériaux. L'utilisation de textures permet de reproduire de petits objets sur la surface, qui nécessiteraient trop de ressources si nous les créions à l'aide de polygones. Il peut s'agir par exemple d'une imitation de pierre, de bois, de la terre ou d'autres matériaux.
CDXMesh et ses classes filles permettent de spécifier une texture. Dans l’ombrage de pixel standard, cette texture est utilisée avec DiffuseColor. Supprimez l'animation de l'objet et appliquez une texture de pierre. Le fichier de la structure est situé dans le dosser MQL5\Files du répertoire de travail du terminal :
virtual bool Create(const int width,const int height) { ... //--- set the white color for the non-directional lighting m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); //--- add texture to draw the cube faces m_box.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- add the cube to the scene m_canvas.ObjectAdd(&m_box); //--- redraw the scene Redraw(); //--- succeed return(true); }

Un cube avec une texture de pierre
Création d’Objets Personnalisés
Tous les objets sont constitués de sommets (DXVector3), connectés en primitives en utilisant des indices. La primitive la plus courante est le triangle. Un objet 3D de base est créé par la création d'une liste de sommets contenant les coordonnées (mais peuvent aussi contenir beaucoup de données supplémentaires, comme la normale, la couleur, etc.), le type de primitives, et une liste d'indices de sommets par lesquels ils seront combinés en primitives.
La bibliothèque standard possède le type de sommet DXVertex, qui contient ses coordonnées, une normale pour le calcul de l'éclairage, les coordonnées et la couleur de la texture. L’ombrage de vertex standard fonctionne avec ce type de vertex.
struct DXVertex
{
DXVector4 position; // vertex coordinates
DXVector4 normal; // normal vector
DXVector2 tcoord; // face coordinate to apply the texture
DXColor vcolor; // color
};
Le fichier auxiliaire MQL5\Include\Canvas\DXDXUtils.mqh contient un ensemble de méthodes permettant de générer la géométrie (sommets et indices) des primitives de base et de charger la géométrie 3D des fichiers .OBJ.
Ajoutez la création d'une sphère et d'un tore, puis appliquez la même texture de pierre :
virtual bool Create(const int width,const int height) { ... // --- vertices and indexes for manually created objects DXVertex vertices[]; uint indices[]; //--- prepare vertices and indices for the sphere if(!DXComputeSphere(0.3f,50,vertices,indices)) return(false); //--- set white color for the vertices DXColor white=DXColor(1.0f,1.0f,1.0f,1.0f); for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- create the sphere object if(!m_sphere.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- set diffuse color for the sphere m_sphere.DiffuseColorSet(DXColor(0.0,1.0,0.0,1.0)); //--- set white specular color m_sphere.SpecularColorSet(white); m_sphere.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- add the sphere to a scene m_canvas.ObjectAdd(&m_sphere); //--- prepare vertices and indices for the torus if(!DXComputeTorus(0.3f,0.1f,50,vertices,indices)) return(false); //--- set white color for the vertices for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- create the torus object if(!m_torus.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- set diffuse color for the torus m_torus.DiffuseColorSet(DXColor(0.0,0.0,1.0,1.0)); m_torus.SpecularColorSet(white); m_torus.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- add the torus to a scene m_canvas.ObjectAdd(&m_torus); //--- redraw the scene Redraw(); //--- succeed return(true); }
Ajoutez une animation pour les nouveaux objets :
void OnTimer(void) { ... m_canvas.LightDirectionSet(light_direction); //--- sphere orbit DXMatrix translation; DXMatrixTranslation(translation,1.1f,0,0); DXMatrixRotationY(rotation,time); DXMatrix transform; DXMatrixMultiply(transform,translation,rotation); m_sphere.TransformMatrixSet(transform); //--- torus orbit with rotation around its axis DXMatrixRotationX(rotation,time*1.3f); DXMatrixTranslation(translation,-2,0,0); DXMatrixMultiply(transform,rotation,translation); DXMatrixRotationY(rotation,time/1.3f); DXMatrixMultiply(transform,transform,rotation); m_torus.TransformMatrixSet(transform); //--- recalculate the 3D scene and draw it in the canvas Redraw(); }
Enregistrez les modifications sous le nom de "Three Objects.mq5" et exécutez le programme.

Figures tournant autour du cube
Surface 3D Basée sur des Données
Divers graphiques sont généralement utilisés pour créer des rapports et analyser des données, tels que des graphiques linéaires, des histogrammes, des camemberts, etc. MQL5 offre une bibliothèque graphique pratique, qui ne permet toutefois de créer que des graphiques en 2D.
La classe CDXSurface permet de visualiser une surface à l'aide des données stockées dans un tableau bidimensionnel. Prenons l'exemple de la fonction mathématique suivante :
z=sin(2.0*pi*sqrt(x*x+y*y))
Créez un objet pour dessiner une surface, et un tableau pour stocker les données :
virtual bool Create(const int width,const int height) { ... //--- prepare an array to store data m_data_width=m_data_height=100; ArrayResize(m_data,m_data_width*m_data_height); for(int i=0;i<m_data_width*m_data_height;i++) m_data[i]=0.0; //--- create a surface object if(!m_surface.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { m_canvas.Destroy(); return(false); } //--- create texture and reflection m_surface.SpecularColorSet(DXColor(1.0,1.0,1.0,1.0)); m_surface.TextureSet(m_canvas.DXDispatcher(),"checker.bmp"); //--- add the surface to the scene m_canvas.ObjectAdd(&m_surface); //--- succeed return(true); }
La surface sera dessinée dans une boîte 4x4 de hauteur 1. Les dimensions de la texture sont de 0,25 x 0,25.
- SF_TWO_SIDED indique que la surface sera dessinée à la fois au-dessus et au-dessous de la surface, au cas où la caméra se déplacerait sous la surface.
- SF_USE_NORMALS indique que les normales seront utilisées pour calculer les réflexions de la surface causées par la source de lumière directionnelle.
- CS_COLD_TO_HOT définit la couleur de la carte thermique de la surface du bleu au rouge, avec une transition par le vert et le jaune.
Pour animer la surface, ajoutez le temps sous le signe de la sinusoïde et actualisez-le une minuterie.
void OnTimer(void) { static ulong last_time=0; static float time=0; //--- get the current time ulong current_time=GetMicrosecondCount(); //--- calculate the delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- increase the elapsed time value time+=deltatime; //--- remember the time last_time=current_time; //--- calculate surface values taking into account time changes for(int i=0; i<m_data_width; i++) { double x=2.0*i/m_data_width-1; int offset=m_data_height*i; for(int j=0; j<m_data_height; j++) { double y=2.0*j/m_data_height-1; m_data[offset+j]=MathSin(2.0*M_PI*sqrt(x*x+y*y)-2*time); } } //--- update data to draw the surface if(m_surface.Update(m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { //--- recalculate the 3D scene and draw it in the canvas Redraw(); } }Le code source est disponible dans le fichier 3D Surface.mq5, l'exemple du programme est montré dans la vidéo.
Dans cet article, nous avons examiné les capacités des fonctions DirectX pour créer des formes géométriques simples et des graphiques 3D animés pour l'analyse visuelle des données. Des exemples plus complexes peuvent être trouvés dans le répertoire d'installation du terminal MetaTrader 5, dans le répertoire d'installation du terminal : Les Expert Advisors "Correlation Matrix 3D" et "Math 3D Morpher", ainsi que le script "Remnant 3D".
MQL5 vous permet de résoudre d'importantes tâches de trading algorithmique sans utiliser de logiciels tiers :
- Optimisation des stratégies de trading complexes avec de nombreux paramètres d'entrée
- Calcul des résultats d'optimisation
- Visualisation des données en 3D
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/7708
 Développer un Expert Advisor à partir de zéro (partie 10) : Accéder aux indicateurs personnalisés
Développer un Expert Advisor à partir de zéro (partie 10) : Accéder aux indicateurs personnalisés
 SQLite Gestion native des bases de données SQL dans MQL5
SQLite Gestion native des bases de données SQL dans MQL5
 Développer un Expert Advisor à partir de zéro (partie 11) : Système d’ordre croisés
Développer un Expert Advisor à partir de zéro (partie 11) : Système d’ordre croisés
 Visualisez le ! Bibliothèque graphique MQL5 similaire à 'plot' du langage R
Visualisez le ! Bibliothèque graphique MQL5 similaire à 'plot' du langage R
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation