Como criar gráficos 3D usando o DirectX no MetaTrader 5
A computação gráfica tridimensional fornece as impressões de objetos tridimensionais em uma tela plana. Tais objetos, bem como a posição do visualizador, podem mudar com o tempo. Consequentemente, a imagem bidimensional também deve ser alterada para criar a ilusão de profundidade da imagem, ou seja, ela deve suportar rotação, zoom, mudanças na iluminação e assim por diante. A MQL5 permite criar e gerenciar gráficos de computador diretamente da plataforma MetaTrader 5 usando as funções DirectX. Observe que sua placa de vídeo deve suportar o DX 11 e o Shader Model 5.0 para que as funções funcionem.
- Modelagem de Objetos
- Criando uma forma
- Cálculo e Renderização de cenas
- Rotação de Objetos em torno do Eixo Z e o Ponto-de-observador
- Gerenciamento de Posição da Câmera
- Gerenciamento de Cores de Objetos
- Rotação e Movimento
- Trabalhando com a Iluminação
- Animação
- Controle da Posição da Câmera Usando o Mouse
- Aplicando Texturas
- Criando objetos Personalizados
- Superfície 3D Baseada em Dados
Modelagem de Objetos
Para desenhar um objeto tridimensional em um espaço plano, deve-se obter primeiro um modelo desse objeto nas coordenadas X, Y e Z. Isso significa que cada ponto na superfície do objeto deve ser descrito especificando suas coordenadas. Idealmente, seria necessário descrever um número infinito de pontos na superfície do objeto para preservar a qualidade da imagem durante o dimensionamento. Na prática, os modelos 3D são descritos usando uma malha composta por polígonos. Uma malha mais detalhada com um número maior de polígonos fornece um modelo mais realista. No entanto, são necessários mais recursos computacionais para calcular esse modelo e renderizar os gráficos 3D.
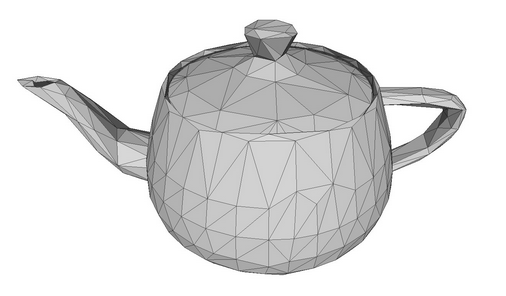
Um modelo de bule como uma malha de polígono.
A divisão dos polígonos em triângulos apareceu há muito tempo, quando os primeiros gráficos computacionais precisavam rodar em placas gráficas fracas. O triângulo permite a descrição exata da posição de uma pequena parte da superfície, bem como o cálculo dos parâmetros relacionados, como luzes e reflexos de luz. A coleção desses pequenos triângulos permite a criação de uma imagem tridimensional realista do objeto. A seguir, o polígono e o triângulo serão usados como sinônimos, pois é muito mais fácil imaginar um triângulo do que um polígono com N vértices.
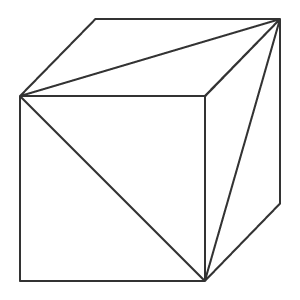
Cubo composto de triângulos.
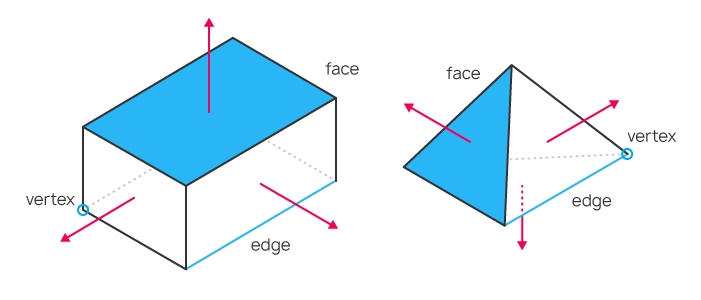
Um modelo tridimensional de um objeto pode ser criado descrevendo as coordenadas de cada vértice do triângulo, o que permite o cálculo adicional de coordenadas para cada ponto do objeto, mesmo que o objeto se mova ou a posição do visualizador se altere. Assim, nós lidamos com os vértices, as arestas que os conectam e a face que é formada pelas arestas. Se a posição de um triângulo é conhecida, nós podemos criar uma normal para a face usando as leis da álgebra linear (uma normal é um vetor que é perpendicular à superfície). Isso permite calcular como o rosto será iluminado e como a luz será refletida a partir dele.
Exemplos de objetos simples com vértices, arestas, faces e normais. A normal representa a seta vermelha.
Um objeto do modelo pode ser criado de diferentes maneiras. A topologia descreve como os polígonos formam a malha 3D. Uma boa topologia permite usar o número mínimo de polígonos para descrever um objeto e pode facilitar o movimento e a rotação do objeto.
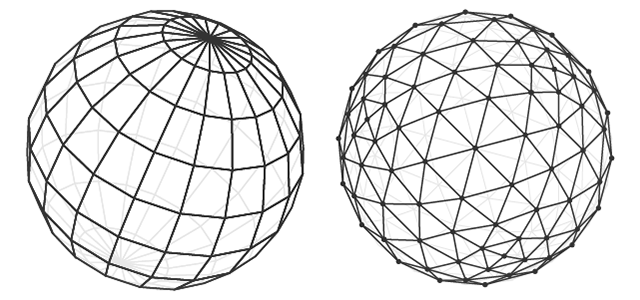
Modelo de esfera em duas topologias.
O efeito do volume é criado usando luzes e sombras nos polígonos do objeto. Assim, o objetivo da computação gráfica em 3D é calcular a posição de cada ponto de um objeto, calcular as luzes e sombras e exibi-lo na tela.
Criando uma forma
Vamos escrever um programa simples que cria um cubo. Utilizaremos a classe CCanvas3D da biblioteca de gráficos 3D.
A classe CCanvas3DWindow, que renderiza uma janela 3D, possui um número mínimo de membros e métodos. Nós adicionaremos gradualmente novos métodos com uma explicação dos conceitos de gráficos 3D implementados nas funções para trabalhar com o DirectX.
//+------------------------------------------------------------------+ //| Janela do aplicativo | //+------------------------------------------------------------------+ class CCanvas3DWindow { protected: CCanvas3D m_canvas; //--- dimensões da tela int m_width; int m_height; //--- objeto Cubo CDXBox m_box; public: CCanvas3DWindow(void) {} ~CCanvas3DWindow(void) {m_box.Shutdown();} //-- criação da cena virtual bool Create(const int width,const int height){} //--- cálculo da cena void Redraw(){} //--- processando os eventos do gráfico void OnChartChange(void) {} };
A criação de uma cena começa com a criação de uma tela. Em seguida, os seguintes parâmetros são definidos para a matriz de projeção:
- Um ângulo de visão de 30 graus (M_PI/6), do qual observamos a cena 3D
- Proporção como uma proporção de largura e altura
- Distância para o plano de recorte próximo (0.1f) e distante (100.f)
Isso significa que apenas os objetos entre essas duas paredes virtuais (0.1f e 100.f) serão renderizados na matriz de projeção. Além disso, o objeto deve cair no ângulo de visão horizontal de 30 graus. Observe que as distâncias e todas as coordenadas em computação gráfica são virtuais. O que importa são as relações entre distâncias e tamanhos, mas não os valores em absoluto.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { //--- salva as dimensões da tela m_width=width; m_height=height; //--- cria uma tela para renderizar uma cena 3D ResetLastError(); if(!m_canvas.CreateBitmapLabel("3D Sample_1",0,0,m_width,m_height,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return(false); } //--- define os parâmetros da matriz de projeção - ângulo de visão, proporção de tela, distância dos planos de corte próximo e distante m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- cria o cubo - passa para ele o gerenciador de recursos, parâmetros da cena e as coordenadas dos dois cantos opostos do cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,5.0),DXVector3(1.0,1.0,7.0))) { m_canvas.Destroy(); return(false); } //--- adiciona o cubo à cena m_canvas.ObjectAdd(&m_box); //--- redesenha a cena Redraw(); //--- sucesso return(true); }
Após a criação da matriz de projeção, nós podemos prosseguir com a construção do objeto 3D — um cubo baseado na classe CDXBox. Para criar um cubo, basta indicar dois vetores apontando para os cantos opostos do cubo. Observando a criação do cubo no modo de depuração, você pode ver o que está acontecendo na DXComputeBox(): a criação de todos os vértices do cubo (suas coordenadas são gravadas na matriz 'vértices'), bem como a divisão das bordas do cubo em triângulos que são enumerados e salvos na matriz 'indiсes'. No total, o cubo possui 8 vértices, 6 faces divididas em 12 triângulos e 36 índices que enumeram os vértices desses triângulos.
Embora o cubo tenha apenas 8 vértices, 24 vetores são criados para descrevê-los, pois um conjunto separado de vértices com uma normal deve ser especificada para cada uma das 6 faces. A direção da normal afetará o cálculo da iluminação para cada face. A ordem na qual os vértices de um triângulo são listados no índice determina quais de seus lados serão visíveis. A ordem na qual os vértices e índices são preenchidos é mostrada no código DXUtils.mqh:
for(int i=20; i<24; i++) vertices[i].normal=DXVector4(0.0,-1.0,0.0,0.0);
As coordenadas de textura para o mapeamento de textura para cada face são descritas no mesmo código:
//--- texture coordinates for(int i=0; i<faces; i++) { vertices[i*4+0].tcoord=DXVector2(0.0f,0.0f); vertices[i*4+1].tcoord=DXVector2(1.0f,0.0f); vertices[i*4+2].tcoord=DXVector2(1.0f,1.0f); vertices[i*4+3].tcoord=DXVector2(0.0f,1.0f); }
Cada um dos 4 vetores da face define um dos 4 ângulos para o mapeamento de textura. Isso significa que uma estrutura de forma quadrada será mapeada para cada face do cubo para renderizar a textura. Obviamente, isso é necessário apenas se a textura estiver definida.
Cálculo e Renderização de cenas
Todos os cálculos devem ser realizados novamente sempre que a cena 3D for alterada. Aqui está a ordem dos cálculos necessários:
- Calcular o centro de cada objeto nas coordenadas do mundo
- Calcular a posição de cada elemento do objeto, ou seja, de cada vértice
- Determinar a profundidade do pixel e sua visibilidade para o visualizador
- Calcular a posição de cada pixel no polígono especificado por seus vértices
- Definir a cor de cada pixel no polígono de acordo com a textura especificada
- Calcular a direção do pixel de luz e seu reflexo
- Aplicar a luz difusa a cada pixel
- Converter todas as coordenadas do mundo em coordenadas da câmera
- Converter as coordenadas da câmera nas coordenadas da matriz de projeção
//+------------------------------------------------------------------+ //| Atualização da cena | //+------------------------------------------------------------------+ void Redraw() { //--- calcula a cena 3D m_canvas.Render(DX_CLEAR_COLOR|DX_CLEAR_DEPTH,ColorToARGB(clrBlack)); //--- atualiza a imagem na tela de acordo com a cena atual m_canvas.Update(); }
No nosso exemplo, o cubo é criado apenas uma vez e não muda mais. Portanto, o quadro na tela só precisará ser alterado se houver alterações no gráfico, como o redimensionamento do gráfico. Nesse caso, as dimensões da tela são ajustadas às dimensões atuais do gráfico, a matriz de projeção é redefinida e uma imagem na tela é atualizada.
//+------------------------------------------------------------------+ //| Processa o evento de alteração do gráfico | //+------------------------------------------------------------------+ void OnChartChange(void) { //--- obtém as dimensões atuais do gráfico int w=(int)ChartGetInteger(0,CHART_WIDTH_IN_PIXELS); int h=(int)ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS); //--- atualiza as dimensões da tela de acordo com o tamanho do gráfico if(w!=m_width || h!=m_height) { m_width =w; m_height=h; //--- redimensiona a tela m_canvas.Resize(w,h); DXContextSetSize(m_canvas.DXContext(),w,h); //--- atualiza a matriz de projeção de acordo com os tamanhos das telas m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- recalcula a cena 3D e renderiza ela na tela Redraw(); } }
Iniciamos o EA "Step1 Create Box.mq5". Você verá um quadrado branco em um fundo preto. Por padrão, a cor branca é definida para os objetos durante a criação. A iluminação ainda não foi definida.
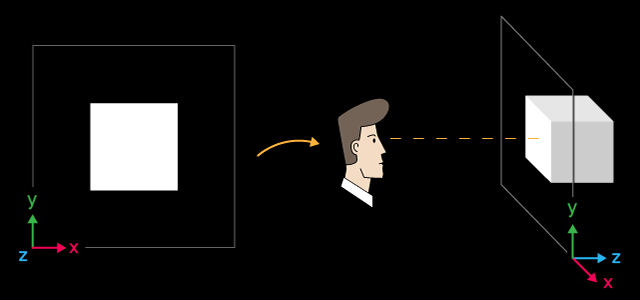
Um cubo branco e seu layout no espaço
O eixo X é orientado para a direita, o Y é orientado para cima e o Z é orientado para dentro da cena 3D. Esse sistema de coordenadas é chamado de left-handed ou orientado para a esquerda.
O centro do cubo está no ponto com as seguintes coordenadas X=0, Y=0, Z=6. A posição da qual olhamos para o cubo está no centro das coordenadas, que é o valor padrão. Se você quiser alterar a posição a partir da qual a cena 3D é exibida, defina explicitamente as coordenadas apropriadas usando a função ViewPositionSet().
Para concluir a operação do programa, pressione "Escape".
Rotação de Objetos em torno do Eixo Z e o Ponto-de-observador
Para animar a cena, permita a rotação do cubo em torno do eixo Z. Para fazer isso, adicionamos um timer — com base em seus eventos, o cubo será girado no sentido anti-horário.
Criamos uma matriz de rotação para ativar a rotação em torno do eixo Z em um determinado ângulo usando o método DXMatrixRotationZ(). Em seguida, passamos ele como parâmetro para o método TransformMatrixSet(). Isso mudará a posição do cubo no espaço 3D. Mais uma vez, chamamos a função Redraw() para atualizar a imagem na tela.
//+------------------------------------------------------------------+ //| Manipulador do timer | //+------------------------------------------------------------------+ void OnTimer(void) { //--- variáveis para calcular o ângulo de rotação static ulong last_time=0; static float angle=0; //--- obtém a hora atual ulong current_time=GetMicrosecondCount(); //--- calcula o delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumenta o ângulo de rotação do cubo ao redor do eixo Z angle+=deltatime; //--- lembra da hora last_time=current_time; //--- define o ângulo de rotação do cubo ao redor do eixo Z DXMatrix rotation; DXMatrixRotationZ(rotation,angle); m_box.TransformMatrixSet(rotation); //--- recalcula a cena 3D e renderiza ela na tela Redraw(); }
Após o seu início, você verá um quadrado branco rotativo.

O cubo gira em torno do eixo Z no sentido anti-horário
O código fonte deste exemplo está disponível no arquivo "Step2 Rotation Z.mq5" Por favor, note que o ângulo M_PI/5 é especificado agora ao criar a cena, que é maior que o ângulo M_PI/6 do exemplo anterior.
//--- define os parâmetros da matriz de projeção - ângulo de visão, proporção de tela, distância dos planos de corte próximo e distante m_matrix_view_angle=(float)M_PI/5; m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- cria o cubo - passa para ele o gerenciador de recursos, parâmetros da cena e as coordenadas dos dois cantos opostos do cubo
No entanto, a dimensão do cubo na tela é visualmente menor. Quanto menor o ângulo de visão que indicamos ao definir a matriz de projeção, maior será a parte do quadro, que é ocupada pelo objeto. Isso pode ser comparado ao funcionamento de um telescópio: o objeto é maior, embora o ângulo de visão seja menor.
Gerenciamento de Posição da Câmera
A classe CCanvas3D possui três métodos para definir os parâmetros importantes da cena 3D, que são interconectados:
- ViewPositionSet define o ponto-de-observação da cena 3D
- ViewTargetSet define as coordenadas do ponto-de-observação
- ViewUpDirectionSet define a direção da borda superior do quadro no espaço 3D
Todos esses parâmetros são usados em combinação — isso significa que, se você deseja definir algum desses parâmetros na cena 3D, os outros dois parâmetros também devem ser inicializados. Isso deve ser feito pelo menos no estágio de geração da cena. Isso é mostrado no exemplo a seguir, no qual a borda superior do quadro oscila para a esquerda e para a direita. A oscilação é implementada adicionando as três linhas de código a seguir no método Create():
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { .... //--- adiciona o cubo à cena m_canvas.ObjectAdd(&m_box); //--- define os parâmetros da cena m_canvas.ViewUpDirectionSet(DXVector3(0,1,0)); // define o vetor de direção para cima, ao longo do eixo Y m_canvas.ViewPositionSet(DXVector3(0,0,0)); // define o ponto-de-observação do centro das coordenadas m_canvas.ViewTargetSet(DXVector3(0,0,6)); // define o ponto-de-observação no centro do cubo //--- redesenha a cena Redraw(); //--- sucesso return(true); }
Modificamos o método OnTimer() para fazer o vetor horizontal girar para a esquerda e direita.
//+------------------------------------------------------------------+ //| Manipulador do timer | //+------------------------------------------------------------------+ void OnTimer(void) { //--- variáveis para calcular o ângulo de rotação static ulong last_time=0; static float max_angle=(float)M_PI/30; static float time=0; //--- obtém a hora atual ulong current_time=GetMicrosecondCount(); //--- calcula o delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumenta o ângulo de rotação do cubo ao redor do eixo Z time+=deltatime; //--- lembra da hora last_time=current_time; //--- define o ângulo de rotação em torno do eixo Z DXVector3 direction=DXVector3(0,1,0); // direção inicial do topo DXMatrix rotation; // vetor de rotação //--- calcula a matriz de rotação DXMatrixRotationZ(rotation,float(MathSin(time)*max_angle)); DXVec3TransformCoord(direction,direction,rotation); m_canvas.ViewUpDirectionSet(direction); // define a nova direção do topo //--- recalcula a cena 3D e renderiza ela na tela Redraw(); }
Salvamos o exemplo como "Step3 ViewUpDirectionSet.mq5" e executamos ele. Você verá a imagem de um cubo oscilante, embora ele esteja realmente imóvel. Este efeito é obtido quando a própria câmera gira para a esquerda e para a direita.

A direção da parte superior oscila a esquerda e direita
Gerenciamento de Cores de Objetos
Vamos modificar nosso código e colocar o cubo no centro das coordenadas, enquanto movemos a câmera.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... //--- cria o cubo - passa para ele o gerenciador de recursos, parâmetros da cena e as coordenadas dos dois cantos opostos do cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- define a cor m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- adiciona o cubo à cena m_canvas.ObjectAdd(&m_box); //--- define as posições para a câmera, o objetivo e a direção da parte superior m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); // define o vetor de direção para cima, ao longo do eixo Y m_canvas.ViewPositionSet(DXVector3(3.0,2.0,-5.0)); // posiciona a câmera à direita, na parte superior e na frente do cubo m_canvas.ViewTargetSet(DXVector3(0,0,0)); // define a direção de observação ao centro do cubo //--- redesenha a cena Redraw(); //--- sucesso return(true); }
Além disso, pintamos o cubo de azul. A cor é definida no formato de cor RGB com um canal alfa (o canal alfa é indicado por último), embora os valores sejam normalizados para um. Assim, um valor 1 significa 255 e 0,5 significa 127.
Adicionamos a rotação ao redor do eixo X e salvamos as alterações como "Step4 Box Color.mq5".

Vista do cubo em rotação para cima e a direita.
Rotação e Movimento
Os objetos podem ser movidos e girados em três direções por vez. Todas as alterações dos objetos são implementadas usando matrizes. Cada um deles, ou seja, rotação, movimento e transformação, pode ser calculado separadamente. Vamos mudar o exemplo: a visão da câmera agora é de cima e de frente.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- posiciona a câmera no topo e na frente do centro de coordenadas m_canvas.ViewPositionSet(DXVector3(0.0,2.0,-5.0)); m_canvas.ViewTargetSet(DXVector3(0.0,0.0,0.0)); m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); //--- cria o cubo - passa para ele o gerenciador de recursos, parâmetros da cena e as coordenadas dos dois cantos opostos do cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- define a cor do cubo m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- calcula a posição do cubo e a matriz de transferência DXMatrix rotation,translation; //--- gira o cubo sequencialmente ao longo dos eixos X, Y e Z DXMatrixRotationYawPitchRoll(rotation,(float)M_PI/4,(float)M_PI/3,(float)M_PI/6); //--- move o cubo para a direita/baixo/dentro DXMatrixTranslation(translation,1.0,-2.0,5.0); //--- obtém a matriz de transformação como um produto de rotação e transferência DXMatrix transform; DXMatrixMultiply(transform,rotation,translation); //--- define a matriz de transformação m_box.TransformMatrixSet(transform); //--- adiciona o cubo à cena m_canvas.ObjectAdd(&m_box); //--- redesenha a cena Redraw(); //--- sucesso return(true); }
Criamos sequencialmente as matrizes de rotação e transferência, aplicamos a matriz de transformação resultante e renderizamos o cubo. Salvamos as alterações em "Step5 Translation.mq5" e executamos ele.

Rotação e movimento de um cubo
A câmera está parada e está apontada para o centro das coordenadas levemente de cima. O cubo foi girado em três direções e foi deslocado para a direita, para baixo e para dentro da cena.
Trabalhando com a Iluminação
Para obter uma imagem tridimensional realista, é necessário calcular a iluminação de cada ponto na superfície do objeto. Isso é feito usando o Modelo de Iluminação de Phong, que calcula a intensidade da cor dos três componentes de iluminação a seguir: ambiente, difuso e especular. Os seguintes parâmetros são usados aqui:
- DirectionLight — a direção da iluminação direcional é definida no CCanvas3D
- AmbientLight — a cor e a intensidade da iluminação ambiente são definidas no CCanvas3D
- DiffuseColor — o componente de iluminação difusa calculado é definido no CDXMesh e em suas classes filho
- EmissionColor — o componente de iluminação de fundo é definido no CDXMesh e em suas classes filho
- SpecularColor — o componente especular é definido no CDXMesh e em suas classes filho

Modelo de Iluminação de Phong
O modelo de iluminação é implementado em shaders padrão, os parâmetros do modelo são definidos no CCanvas3D e os parâmetros do objeto são definidos no CDXMesh e em suas classes filho. Modificamos o exemplo da seguinte maneira:
- Retornamos o cubo ao centro de coordenadas.
- Definimos a cor branca.
- Adicionamos uma fonte direcional de cor amarela que ilumina a cena de cima para baixo.
- Definimos a cor azul para a iluminação não direcional.
//--- define a cor amarela da fonte e direciona-a de cima para baixo m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- define a cor azul para a luz ambiente m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); //--- cria o cubo - passa para ele o gerenciador de recursos, parâmetros da cena e as coordenadas dos dois cantos opostos do cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- define a cor branca do cubo m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); //--- adiciona brilho verde ao cubo (emissão) m_box.EmissionColorSet(DXColor(0.0,1.0,0.0,0.2f));
Observe que a posição da fonte de luz direcionada não está definida no Canvas3D, enquanto apenas a direção na qual a luz se espalha é dada. A fonte da luz direcional é considerada uma distância infinita e um fluxo de luz estritamente paralelo ilumina a cena.
m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0));
Aqui, o vetor de propagação da luz é apontado ao longo do eixo Y na direção negativa, ou seja, de cima para baixo. Além disso, se você definir parâmetros para a fonte de luz direcionada (LightColorSet e LightDirectionSet), também deverá especificar a cor da luz ambiente (AmbientColorSet). Por padrão, a cor da luz ambiente é definida como branca com intensidade máxima e, portanto, todas as sombras serão brancas. Isso significa que os objetos na cena serão iluminados com branco pela iluminação ambiente, enquanto a luz direcional da fonte será interrompida pela luz branca.
//--- define a cor amarela da fonte e direciona-a de cima para baixo m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- define a cor azul para a luz ambiente m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); // deve ser especificado
A animação gif abaixo mostra como a imagem muda quando nós adicionamos iluminação. O código fonte do exemplo está disponível no arquivo "Step6 Add Light.mq5".

O cubo branco com emissão verde sob uma fonte de luz amarela, com luz ambiente azul
Tente desativar os métodos de cores no código acima para ver como ele funciona.
Animação
A animação implica uma mudança nos parâmetros e objetos da cena ao longo do tempo. Quaisquer propriedades disponíveis podem ser alteradas dependendo da hora ou dos eventos. Define o timer para 10 milissegundos — este evento afetará a atualização da cena:
int OnInit() { ... //--- cria a tela ExtAppWindow=new CCanvas3DWindow(); if(!ExtAppWindow.Create(width,height)) return(INIT_FAILED); //--- define o timer EventSetMillisecondTimer(10); //--- return(INIT_SUCCEEDED); }
Adiciona o manipulador de eventos apropriado ao CCanvas3DWindow. Nós precisamos alterar os parâmetros do objeto (como rotação, movimento e zoom) e a direção da iluminação:
//+------------------------------------------------------------------+ //| Manipulador do timer | //+------------------------------------------------------------------+ void OnTimer(void) { static ulong last_time=0; static float time=0; //--- obtém a hora atual ulong current_time=GetMicrosecondCount(); //--- calcula o delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumenta o valor do tempo decorrido time+=deltatime; //--- lembra da hora last_time=current_time; //--- calcula a posição do cubo e a matriz de rotação DXMatrix rotation,translation,scale; DXMatrixRotationYawPitchRoll(rotation,time/11.0f,time/7.0f,time/5.0f); DXMatrixTranslation(translation,(float)sin(time/3),0.0,0.0); //--- calcula a compressão/extensão do cubo ao longo dos eixos DXMatrixScaling(scale,1.0f+0.5f*(float)sin(time/1.3f),1.0f+0.5f*(float)sin(time/1.7f),1.0f+0.5f*(float)sin(time/1.9f)); //--- multiplica as matrizes para obter a transformação final DXMatrix transform; DXMatrixMultiply(transform,scale,rotation); DXMatrixMultiply(transform,transform,translation); //--- define a matriz de transformação m_box.TransformMatrixSet(transform); //--- calcula a rotação da fonte de luz em torno do eixo Z DXMatrixRotationZ(rotation,deltatime); DXVector3 light_direction; //--- obtém a direção atual da fonte de luz m_canvas.LightDirectionGet(light_direction); //--- calcula a nova direção da fonte de luz e define ela DXVec3TransformCoord(light_direction,light_direction,rotation); m_canvas.LightDirectionSet(light_direction); //--- recalcula a cena 3D e desenha ela na tela Redraw(); }
Observe que as alterações do objeto são aplicadas sobre os valores iniciais, como se sempre lidássemos com o estado inicial do cubo e aplicássemos todas as operações relacionadas à rotação/movimento/compressão do zero, o que significa que o estado atual do cubo não é salvo. No entanto, a direção da fonte de luz é alterada por incrementos deltatime a partir do valor atual.

Um cubo em rotação com a direção da fonte de luz que muda dinamicamente.
O resultado é uma animação 3D bem complexa. O código de exemplo está disponível no arquivo "Step7 Animation.mq5".
Controle da Posição da Câmera Usando o Mouse
Vamos considerar o último elemento de animação nos gráficos 3D, uma reação às ações do usuário. Adicionamos o gerenciamento da câmera usando o mouse em nosso exemplo. Primeiro, aderimos aos eventos do mouse e criamos os manipuladores correspondentes:
int OnInit() { ... //--- define o timer EventSetMillisecondTimer(10); //--- ativa o recebimento de eventos do mouse: cliques em movimento e botão ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,1); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,1) //--- return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { //--- Remove o timer EventKillTimer(); //--- desativa o recebimento de eventos do mouse ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,0); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,0); //--- remove o objeto delete ExtAppWindow; //--- retorna o gráfico ao modo de exibição usual com os gráficos de preços ChartSetInteger(0,CHART_SHOW,true); } void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam) { ... //--- evento de alteração do gráfico if(id==CHARTEVENT_CHART_CHANGE) ExtAppWindow.OnChartChange(); //--- evento de movimento do mouse if(id==CHARTEVENT_MOUSE_MOVE) ExtAppWindow.OnMouseMove((int)lparam,(int)dparam,(uint)sparam); //--- evento de rolagem da roda do mouse if(id==CHARTEVENT_MOUSE_WHEEL) ExtAppWindow.OnMouseWheel(dparam);
No CCanvas3DWindow, criamos o manipulador de eventos de movimento do mouse. Ele mudará os ângulos de direção da câmera quando o mouse for movido com o botão esquerdo pressionado:
//+------------------------------------------------------------------+ //| Processando os movimentos do mouse | //+------------------------------------------------------------------+ void OnMouseMove(int x,int y,uint flags) { //--- botão esquerdo do mouse if((flags&1)==1) { //--- não há informações sobre a posição anterior do mouse if(m_mouse_x!=-1) { //--- atualiza o ângulo da câmera ao mudar de posição m_camera_angles.y+=(x-m_mouse_x)/300.0f; m_camera_angles.x+=(y-m_mouse_y)/300.0f; //--- define o ângulo vertical no intervalo entre (-Pi/2, Pi2) if(m_camera_angles.x<-DX_PI*0.49f) m_camera_angles.x=-DX_PI*0.49f; if(m_camera_angles.x>DX_PI*0.49f) m_camera_angles.x=DX_PI*0.49f; //--- atualiza a posição da câmera UpdateCameraPosition(); } //--- salva a posição do mouse m_mouse_x=x; m_mouse_y=y; } else { //--- redefine a posição salva se o botão esquerdo do mouse não for pressionado m_mouse_x=-1; m_mouse_y=-1; } }
Aqui está o manipulador de eventos da roda do mouse, que altera a distância entre a câmera e o centro da cena:
//+------------------------------------------------------------------+ //| Processando os eventos da roda do mouse | //+------------------------------------------------------------------+ void OnMouseWheel(double delta) { //--- atualiza a distância entre a câmera e o centro em uma rolagem do mouse m_camera_distance*=1.0-delta*0.001; //--- define a distância no intervalo entre [3,50] if(m_camera_distance>50.0) m_camera_distance=50.0; if(m_camera_distance<3.0) m_camera_distance=3.0; //--- atualiza a posição da câmera UpdateCameraPosition(); }
Ambos os manipuladores chamam o método UpdateCameraPosition() para atualizar a posição da câmera de acordo com os parâmetros atualizados:
//+------------------------------------------------------------------+ //| Atualiza a posição da câmera | //+------------------------------------------------------------------+ void UpdateCameraPosition(void) { //--- a posição da câmera levando em consideração a distância ao centro das coordenadas DXVector4 camera=DXVector4(0.0f,0.0f,-(float)m_camera_distance,1.0f); //--- rotação da câmera em torno do eixo X DXMatrix rotation; DXMatrixRotationX(rotation,m_camera_angles.x); DXVec4Transform(camera,camera,rotation); //--- rotação da câmera em torno do eixo Y DXMatrixRotationY(rotation,m_camera_angles.y); DXVec4Transform(camera,camera,rotation); //--- coloca a câmera na posição m_canvas.ViewPositionSet(DXVector3(camera)); }
O código fonte está disponível no arquivo "Step8 Mouse Control.mq5".

Controle da posição da câmera usando o mouse.
Aplicando Texturas
Uma textura é uma imagem bitmap aplicada à superfície de um polígono para representar os padrões ou materiais. O uso de texturas permite reproduzir pequenos objetos na superfície, o que exigiria muitos recursos se os criássemos usando os polígonos. Por exemplo, isso pode ser uma imitação de pedra, madeira, solo e outros materiais.
CDXMesh e suas classes filho permitem especificar a textura. No pixel shader padrão, essa textura é usada junto com o DiffuseColor. Removemos a animação do objeto e aplicamos uma textura de pedra. Ele deve estar localizado na pasta MQL5\Files do diretório de trabalho da plataforma:
virtual bool Create(const int width,const int height) { ... //--- define a cor branca para a iluminação não direcional m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); //--- adiciona a textura para desenhar as faces do cubo m_box.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- adiciona o cubo à cena m_canvas.ObjectAdd(&m_box); //--- redesenha a cena Redraw(); //--- sucesso return(true); }

Um cubo com uma textura de pedra.
Criando objetos Personalizados
Todos os objetos consistem em vértices (DXVector3), que são conectados às primitivas usando índices. A primitiva mais comum é um triângulo. Um objeto 3D básico é criado através da criação de uma lista de vértices que contêm pelo menos coordenadas (mas também pode conter muitos dados adicionais, como a normal, cor etc.), o tipo de primitiva na qual elas são combinadas e um lista de índices de vértices pelos quais eles serão combinados em primitivas.
A Biblioteca padrão possui o tipo de vértice DXVertex, que contém sua coordenada, a normal para o cálculo de iluminação, coordenadas de textura e cor. O sombreador de vértice padrão funciona com esse tipo de vértice.
struct DXVertex
{
DXVector4 position; // coordenadas do vértice
DXVector4 normal; // vetor normal
DXVector2 tcoord; // coordenada da face para aplicar a textura
DXColor vcolor; // cor
};
O tipo auxiliar MQL5\Include\Canvas\DXDXUtils.mqh contém um conjunto de métodos para gerar a geometria (vértices e índices) das primitivas básicas e carregar a geometria 3D de arquivos .OBJ.
Adicionamos a criação de uma esfera e um torus, aplicamos a mesma textura de pedra:
virtual bool Create(const int width,const int height) { ... //--- vértices e índices para objetos criados manualmente DXVertex vertices[]; uint indices[]; //--- prepara vértices e índices para a esfera if(!DXComputeSphere(0.3f,50,vertices,indices)) return(false); //--- define a cor branca para os vértices DXColor white=DXColor(1.0f,1.0f,1.0f,1.0f); for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- cria o objeto de esfera if(!m_sphere.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- define a cor difusa para a esfera m_sphere.DiffuseColorSet(DXColor(0.0,1.0,0.0,1.0)); //--- define a cor especular branca m_sphere.SpecularColorSet(white); m_sphere.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- adiciona a esfera a uma cena m_canvas.ObjectAdd(&m_sphere); //--- prepara as vértices e índices para o torus if(!DXComputeTorus(0.3f,0.1f,50,vertices,indices)) return(false); //--- define a cor branca para os vértices for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- cria o objeto torus if(!m_torus.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- define a cor difusa para o torus m_torus.DiffuseColorSet(DXColor(0.0,0.0,1.0,1.0)); m_torus.SpecularColorSet(white); m_torus.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- adiciona o torus a uma cena m_canvas.ObjectAdd(&m_torus); //--- redesenha a cena Redraw(); //--- sucesso return(true); }
Adiciona animação para os novos objetos:
void OnTimer(void) { ... m_canvas.LightDirectionSet(light_direction); //--- órbita da esfera DXMatrix translation; DXMatrixTranslation(translation,1.1f,0,0); DXMatrixRotationY(rotation,time); DXMatrix transform; DXMatrixMultiply(transform,translation,rotation); m_sphere.TransformMatrixSet(transform); //--- órbita do torus com rotação em torno do seu eixo DXMatrixRotationX(rotation,time*1.3f); DXMatrixTranslation(translation,-2,0,0); DXMatrixMultiply(transform,rotation,translation); DXMatrixRotationY(rotation,time/1.3f); DXMatrixMultiply(transform,transform,rotation); m_torus.TransformMatrixSet(transform); //--- recalcula a cena 3D e desenha ela na tela Redraw(); }
Salvamos as alterações como Three Objects.mq5 e executamos ele.

Figuras que rotacionam na órbita do cubo.
Superfície 3D Baseada em Dados
Vários gráficos são geralmente usados para criar relatórios e analisar dados, como gráficos lineares, histogramas, diagramas de pizza etc. A MQL5 oferece uma conveniente biblioteca gráfica, que no entanto só pode criar gráficos 2D.
A classe CDXSurface permite visualizar uma superfície usando dados personalizados armazenados em uma matriz bidimensional. Vamos ver o exemplo da seguinte função matemática
z=sin(2.0*pi*sqrt(x*x+y*y))
Criamos um objeto para desenhar a superfície e uma matriz para armazenar os dados:
virtual bool Create(const int width,const int height) { ... //--- prepara uma matriz para armazenar os dados m_data_width=m_data_height=100; ArrayResize(m_data,m_data_width*m_data_height); for(int i=0;i<m_data_width*m_data_height;i++) m_data[i]=0.0; //--- cria um objeto de superfície if(!m_surface.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { m_canvas.Destroy(); return(false); } //--- cria textura e reflexão m_surface.SpecularColorSet(DXColor(1.0,1.0,1.0,1.0)); m_surface.TextureSet(m_canvas.DXDispatcher(),"checker.bmp"); //--- adiciona a superfície à cena m_canvas.ObjectAdd(&m_surface); //--- sucesso return(true); }
A superfície será desenhada dentro de uma caixa com uma base de 4x4 e uma altura de 1. As dimensões da textura são 0.25x0.25.
- SF_TWO_SIDED indica que a superfície será desenhada acima e abaixo da superfície, caso a câmera se mova sob a superfície.
- SF_USE_NORMALS indica que os cálculos das normais serão usados para calcular as reflexões da superfície causadas pela fonte de luz direcional.
- CS_COLD_TO_HOT define a coloração do mapa de calor da superfície de azul para vermelho com uma transição entre verde e amarelo.
Para animar a superfície, adicionamos o tempo abaixo do sinal senoidal e atualizamos ele através do timer.
void OnTimer(void) { static ulong last_time=0; static float time=0; //--- obtém a hora atual ulong current_time=GetMicrosecondCount(); //--- calcula o delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumenta o valor do tempo decorrido time+=deltatime; //--- lembra da hora last_time=current_time; //--- calculamos os valores da superfície levando em consideração as mudanças de tempo for(int i=0; i<m_data_width; i++) { double x=2.0*i/m_data_width-1; int offset=m_data_height*i; for(int j=0; j<m_data_height; j++) { double y=2.0*j/m_data_height-1; m_data[offset+j]=MathSin(2.0*M_PI*sqrt(x*x+y*y)-2*time); } } //--- atualizamos os dados para desenhar a superfície if(m_surface.Update(m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { //--- recalcula a cena 3D e desenha ela na tela Redraw(); } }O código fonte está disponível em 3D Surface.mq5, o programa de exemplo é mostrado no vídeo.
Neste artigo, nós consideramos os recursos das Funções DirectX na criação de formas geométricas simples e gráficos 3D animados para a análise visual de dados. Exemplos mais complexos podem ser encontrados no diretório de instalação da plataforma MetaTrader 5: Expert Advisors "Correlation Matrix 3D" e "Math 3D Morpher", além do script "Remnant 3D".
A MQL5 permite resolver tarefas importantes de negociação algorítmica sem usar pacotes de terceiros:
- Otimizar estratégias de negociação complexas que contêm muitos parâmetros de entrada
- Obter resultados de otimização
- Visualizar os dados obtidos usando imagens tridimensionais de uma maneira mais conveniente
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/7708
 Implementando OLAP na negociação (Parte 3): analisando cotações para desenvolver estratégias de negociação
Implementando OLAP na negociação (Parte 3): analisando cotações para desenvolver estratégias de negociação
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso