Buscando patrones estacionales en el mercado de divisas con la ayuda del algoritmo CatBoost

Introducción

Ya hemos dedicado a la búsqueda de patrones estacionales dos artículos (1, 2). Nos interesaba ver cómo de bien puede emprender un algoritmo de aprendizaje de máquinas la detección de dichos patrones. Si recordamos el enfoque de los artículos mencionados, los sistemas comerciales se basaban en el análisis estadístico. Ahora, podremos descartar el factor humano, diciéndole simplemente al modelo: "Quiero que comercies a una hora determinada de un día concreto de la semana". Así, podremos delegar en el algoritmo la búsqueda de patrones.

Función de filtrado de tiempo

Podemos expandir la biblioteca fácilmente añadiendo una función de filtrado adicional.

def time_filter(data, count):
    # filter by hour
    hours=[15]
    if data.index[count].hour not in hours:
        return False

    # filter by day of week
    days = [1]
    if data.index[count].dayofweek not in days:
        return False

    return True

La función verifica las condiciones establecidas dentro de ella. Podemos añadir condiciones adicionales (no solo filtros de tiempo). Pero como en el artículo hablamos de patrones estacionales, usaremos solo filtros de tiempo. Si ejecutamos todas las condiciones, la función retornará True y la muestra correspondiente se añadirá a la muestra de entrenamiento. Por ejemplo, en este caso en particular, le indicamos a los modelos que pueden abrir transacciones solo en la 15ª hora del martes. Las listas hours y days pueden complementarse con otras horas y días. Si comentamos todas las condiciones, el algoritmo funcionará sin las condiciones, como ya sucedía en el artículo anterior. 

La función add_labels ahora recibe a la entrada esta condición. En el lenguaje Python, las funciones son objetos de primer nivel, por lo que podemos transmitirlas de forma segura como argumentos a otras funciones.

def add_labels(dataset, min, max, filter=time_filter):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]
        if filter(dataset, i):
            if future_pr + MARKUP < curr_pr:
                labels.append(1.0)
            elif future_pr - MARKUP > curr_pr:
                labels.append(0.0)
            else:
                labels.append(2.0)
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2].index)

    return dataset

Después de transmitir el filtro a la función, podemos utilizarlo para marcar las transacciones de compra o venta. El filtro, a su vez, recibe el conjunto de datos original y el índice de la barra actual. Los índices del conjunto de datos se presentan como datetime index que contienen la fecha y la hora. El filtro busca la hora y el día en el datetime index del conjunto de datos según el i-ésimo número ordinal y retorna False si no encuentra nada. Si se ejecuta la condición, la transacción se marcará como 1 o 0; de lo contrario, como 2. Al final, todos los doses se eliminan del conjunto de datos de entrenamiento, por lo que solo quedan los ejemplos para los días y horas específicos definidos por el filtro.

También debemos añadir al simulador personalizado un filtro para que las transacciones se abran en un momento determinado (o según cualquier otra condición implementada en el filtro).

def tester(dataset, markup=0.0, plot=False, filter=time_filter):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        ind = dataset.index[i].hour
        if last_deal == 2 and filter(dataset, i):
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue
        if last_deal == 0 and pred > 0.5:
            last_deal = 2
            report.append(report[-1] - markup +
                          (dataset['close'][i] - last_price))
            continue
        if last_deal == 1 and pred < 0.5:
            last_deal = 2
            report.append(report[-1] - markup +
                          (last_price - dataset['close'][i]))

    y = np.array(report).reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.plot(lr.predict(X))
        plt.title("Strategy performance")
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l

Hemos implementado esto de la forma que sigue. La ausencia de una posición abierta se indica con el número 2, es decir, last_deal = 2. Antes de realizar las pruebas, no tenemos posiciones abiertas, por lo que pondremos 2. Iteramos por todo el conjunto de datos y verificamos si se han cumplido las condiciones del filtro. Si es así, abrimos una transacción de compra o venta. La condición del filtro ya no actúa sobre el cierre de las transacciones, porque podemos cerrarlas en otra hora e incluso día de la semana. En realidad, estos son todos los cambios necesarios para realizar correctamente el entrenamiento y las pruebas. 

Análisis de exploración para cada hora comercial.

Poner a prueba el modelo manualmente con cada condición aparte (ya sea una combinación de horas o días) no resulta demasiado conveniente. Para ello, hemos escrito una característica especial que nos permitirá obtener estadísticas resumidas para cada condición por separado. La función puede tardar bastante en completarse, pero en la salida, podremos ver inmediatamente los rangos temporales en los que el modelo funciona de la mejor forma posible.

def exploratory_analysis():
    h = [x for x in range(24)]
    result = pd.DataFrame()
    for _h in h:
        global hours 
        hours = [_h]
        pr = get_prices(START_DATE, STOP_DATE)
        pr = add_labels(pr, min=15, max=15, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 10
        for i in range(iterations):
            res.append(brute_force(10000, gmm))
            print('Iteration: ', i, 'R^2: ', res[-1][0], ' hour= ', _h)
        
        r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h))
        result = result.append(r)

    plt.scatter(result.index, result, c = result.index)
    plt.show()
    return result

En la función, podemos establecer una lista de horas que deben analizarse. Aquí se indican las 24 horas del día al completo. Para que el experimento resulte más puro, hemos desactivado la selección aleatoria, poniendo MIN y MAX (horizonte mínimo y máximo de una posición abierta) igual a 15. La variable "iterations" es responsable del número de reentrenamientos por cada hora. Aumentando este parámetro, podemos obtener estadísticas más fiables. Cuando el trabajo haya finalizado, la función mostrará el gráfico siguiente:

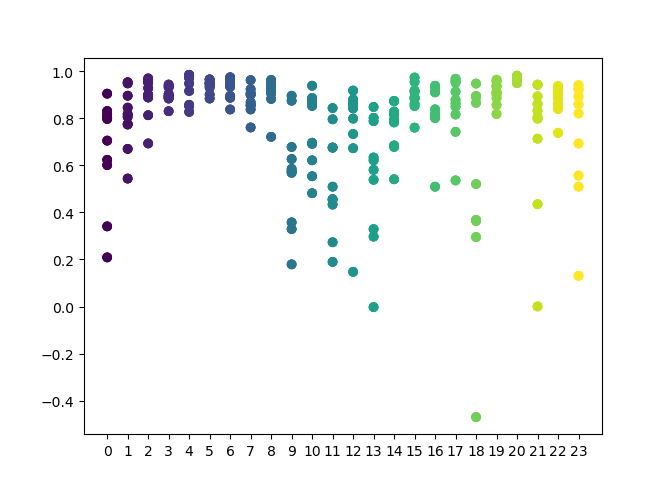
En el eje X se ubica el número ordinal de las horas. En el eje Y, se muestran las estimaciones R^2 para cada iteración (se han seleccionado 10 iteraciones, es decir, los reentrenamientos del modelo para cada hora). Podemos ver claramente que para las horas 4,5 y 6, todas las pasadas están más concentradas, lo cual ofrece más confianza como patrón localizado. Aquí, el principio de selección resulta bastante simple: cuanto más alto y concentrado sea el punto, mejor será el modelo. Por ejemplo, en el intervalo 9-15, el programa muestra una gran dispersión, y la calidad promedio de los modelos se reduce al nivel 0.6. Tras elegir las horas que nos interesan, podemos volver a entrenar el modelo y comprobar sus resultados en el simulador personalizado.

Pruebas de los modelos seleccionados

Hemos realizado el análisis de exploración con la pareja de divisas GBPUSD y los siguientes parámetros:

SYMBOL = 'GBPUSD'
MARKUP = 0.00010
TIMEFRAME = mt5.TIMEFRAME_H1
START_DATE = datetime(2017, 1, 1)
TSTART_DATE = datetime(2015, 1, 1)
FULL_DATE = datetime(2015, 1, 1)
STOP_DATE = datetime(2021, 1, 1)

Por consiguiente, al realizar la prueba, utilizaremos estos mismos. Para mayor confianza, podremos cambiar Full_Date y ver cómo ha funcionado el modelo con los anteriores datos históricos.

El clúster de las horas 3,4,5 y 6 se ha dibujado bien. Podemos suponer que las horas colindantes tienen patrones similares, así que podemos entrenar el modelo para todas estas horas.

hours = [3,4,5,6]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=15, max=15, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)

# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
    n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

# iterative learning
res = []

for i in range(10):
    res.append(brute_force(10000, gmm))
    print('Iteration: ', i, 'R^2: ', res[-1][0])

# test best model
res.sort()
test_model(res[-1])

El resto del código no requiere de explicaciones, ya lo hemos analizado a fondo en artículos anteriores. Solo cabe señalar que, en lugar de un GMM simple, podemos utilizar un modelo bayesiano comentado. No obstante, se trata de una idea experimental y sin comentarios. 

El modelo ideal después de realizar el muestreo de transacciones tendrá el aspecto siguiente:

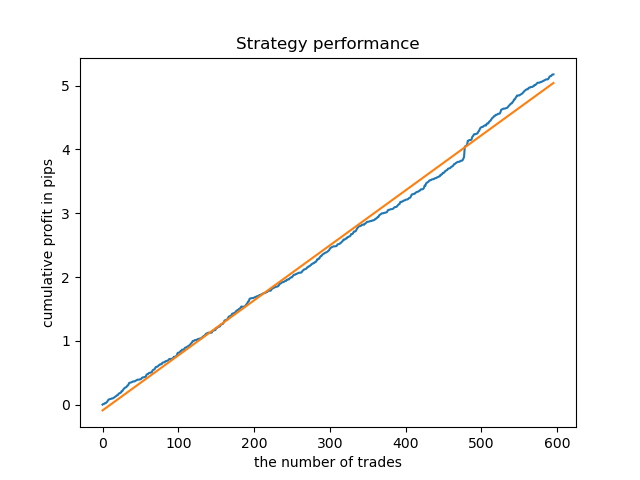
El modelo entrenado (incluidos los datos de prueba) muestra este rendimiento:

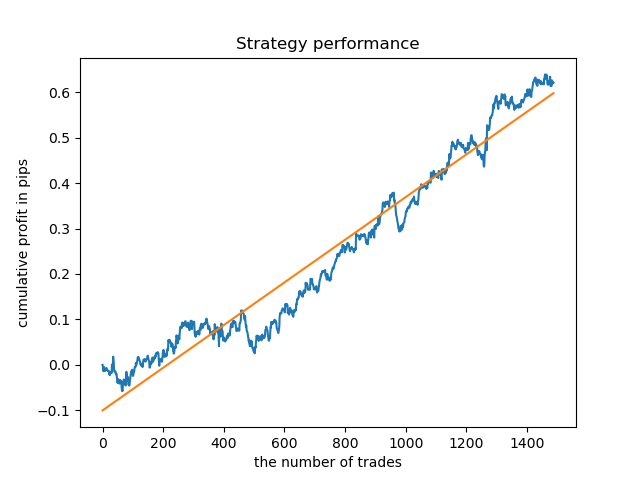
Podemos entrenar modelos aparte para las horas más "concentradas". Este sería el aspecto del gráfico de balances de los modelos ya entrenados para las horas 5 y 20:

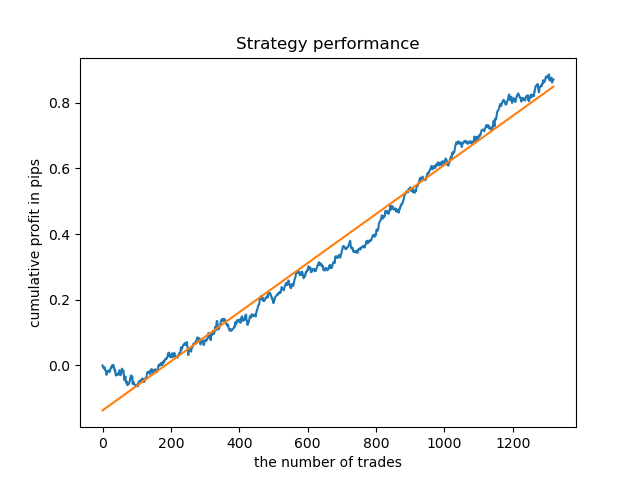
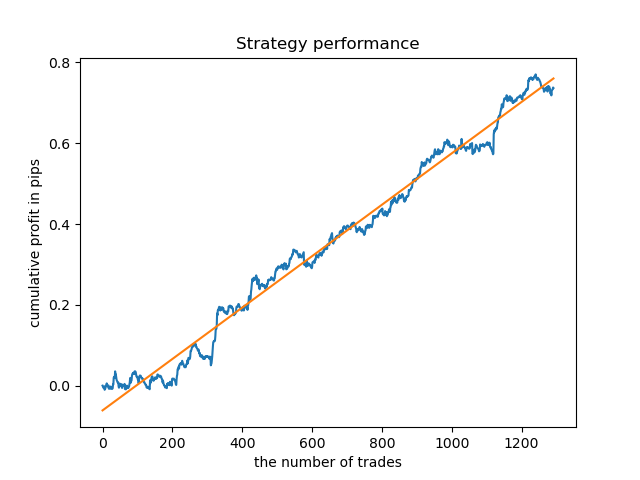
Ahora, a modo de comparación, podemos mirar los modelos entrenados en las horas con una gran dispersión. Tomaremos, por ejemplo, las horas 9 y 11.

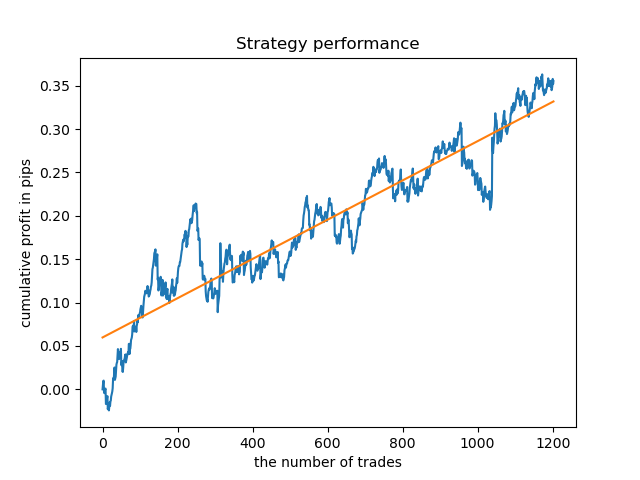
Los gráficos de balance aquí resultan más elocuentes que cualquier comentario. Obviamente, al entrenar los modelos, debemos prestar especial atención a su "timing". 

Análisis de exploración para cada día comercial

Podemos modificar fácilmente el filtro para otros intervalos temporales, por ejemplo, para los días de la semana. Bastará con reemplazar la comprobación de una hora con la comprobación de un día de la semana.

def time_filter(data, count):
    # filter by day of week
    global hours
    if data.index[count].dayofweek not in hours:
        return False
    return True

En este caso, debemos realizar la iteración en el rango que va de 0 a 5 (excluyendo el 5º número ordinal, que sería el sábado).

def exploratory_analysis():
    h = [x for x in range(5)]

Ahora, podemos efectuar un análisis de exploración para la pareja de divisas GBPUSD. La frecuencia de las transacciones, o más bien, su horizonte, ha permanecido igual (15 barras)

pr = add_labels(pr, min=15, max=15, filter=time_filter)

El proceso de aprendizaje se muestra en la consola, donde podemos ver inmediatamente las estimaciones R^2 para el periodo actual. Aquí, la variable "hour" no contiene el número ordinal de la hora, sino el número ordinal del día.

Iteration:  0 R^2:  0.5297625368835237  hour=  0
Iteration:  1 R^2:  0.8166096906047893  hour=  0
Iteration:  2 R^2:  0.9357674260125702  hour=  0
Iteration:  3 R^2:  0.8913802241811986  hour=  0
Iteration:  4 R^2:  0.8079720208707672  hour=  0
Iteration:  5 R^2:  0.8505663844866759  hour=  0
Iteration:  6 R^2:  0.2736870273207084  hour=  0
Iteration:  7 R^2:  0.9282442121644887  hour=  0
Iteration:  8 R^2:  0.8769775718602929  hour=  0
Iteration:  9 R^2:  0.7046666925774866  hour=  0
Iteration:  0 R^2:  0.7492883761480897  hour=  1
Iteration:  1 R^2:  0.6101962958733655  hour=  1
Iteration:  2 R^2:  0.6877652983219245  hour=  1
Iteration:  3 R^2:  0.8579669286548137  hour=  1
Iteration:  4 R^2:  0.3822441930760343  hour=  1
Iteration:  5 R^2:  0.5207801806491617  hour=  1
Iteration:  6 R^2:  0.6893157850263495  hour=  1
Iteration:  7 R^2:  0.5799059801202937  hour=  1
Iteration:  8 R^2:  0.8228326786957887  hour=  1
Iteration:  9 R^2:  0.8742262956151615  hour=  1
Iteration:  0 R^2:  0.9257707800422799  hour=  2
Iteration:  1 R^2:  0.9413981795880517  hour=  2
Iteration:  2 R^2:  0.9354221623113591  hour=  2
Iteration:  3 R^2:  0.8370429185837882  hour=  2
Iteration:  4 R^2:  0.9142875737195697  hour=  2
Iteration:  5 R^2:  0.9586871067966855  hour=  2
Iteration:  6 R^2:  0.8209392060391961  hour=  2
Iteration:  7 R^2:  0.9457287035542066  hour=  2
Iteration:  8 R^2:  0.9587372191281025  hour=  2
Iteration:  9 R^2:  0.9269140213952402  hour=  2
Iteration:  0 R^2:  0.9001009579436263  hour=  3
Iteration:  1 R^2:  0.8735623527502183  hour=  3
Iteration:  2 R^2:  0.9460714774572146  hour=  3
Iteration:  3 R^2:  0.7221720163838841  hour=  3
Iteration:  4 R^2:  0.9063579778744433  hour=  3
Iteration:  5 R^2:  0.9695391076372475  hour=  3
Iteration:  6 R^2:  0.9297881558889788  hour=  3
Iteration:  7 R^2:  0.9271590681844957  hour=  3
Iteration:  8 R^2:  0.8817985496711311  hour=  3
Iteration:  9 R^2:  0.915205007218742   hour=  3
Iteration:  0 R^2:  0.9378516360378022  hour=  4
Iteration:  1 R^2:  0.9210968481902528  hour=  4
Iteration:  2 R^2:  0.9072205941748894  hour=  4
Iteration:  3 R^2:  0.9408826184927528  hour=  4
Iteration:  4 R^2:  0.9671981453714584  hour=  4
Iteration:  5 R^2:  0.9625144032389237  hour=  4
Iteration:  6 R^2:  0.9759244293257822  hour=  4
Iteration:  7 R^2:  0.9461473783201281  hour=  4
Iteration:  8 R^2:  0.9190627222826241  hour=  4
Iteration:  9 R^2:  0.9130350931314233  hour=  4

No olvidemos que todos los modelos han sido entrenados desde principios de 2017, mientras que la estimación R^2 se ha realizado considerando el segmento de prueba (datos adicionales a partir de 2015). La secuencia de altas valoraciones para cada día nos ofrece confianza adicional. Vamos a mostrar el resultado final.

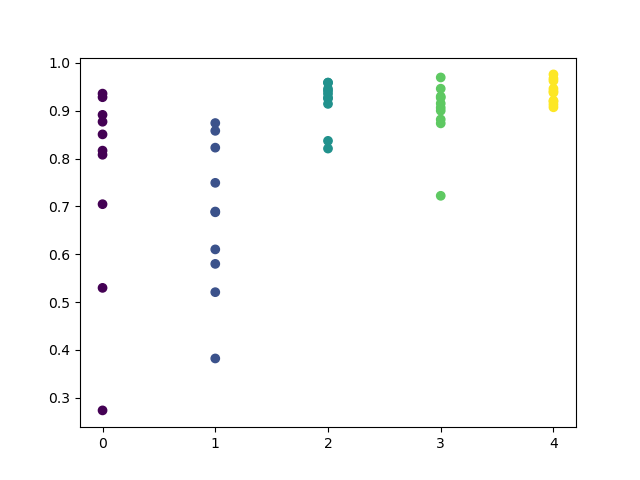
El análisis de exploración ha mostrado que el miércoles y el viernes son los días más favorables para el comercio, especialmente el viernes. El peor día ha resultado el martes: tiene una gran dispersión de errores y un valor bajo de los mismos. Vamos a entrenar el modelo para comerciar solo el viernes; luego echaremos un vistazo al resultado.

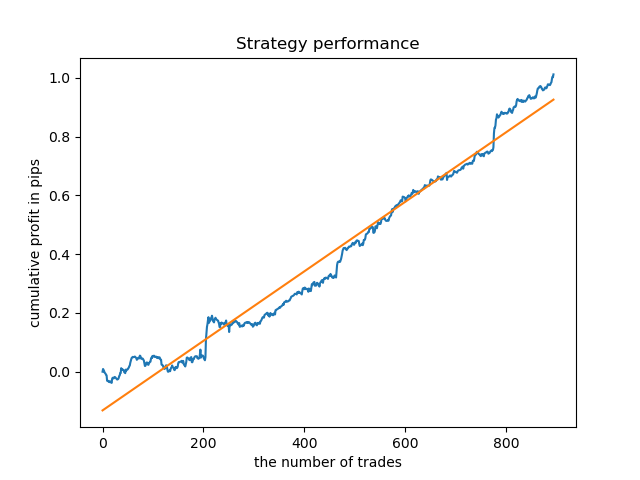
De la misma forma, podemos obtener un modelo que comercie solo el martes.

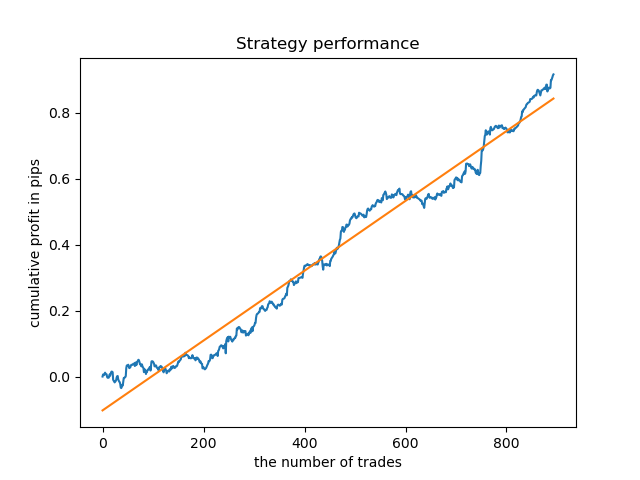
La duración fija de las transacciones no siempre puede justificarse, por consiguiente, tendrá sentido ampliar el cuadro de búsqueda y aumentar el número de iteraciones de análisis de exploración hasta 20.

pr = add_labels(pr, min=5, max=25, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 20

La dispersión de los valores ha aumentado; los mejores días para el comercio son los jueves y los viernes.

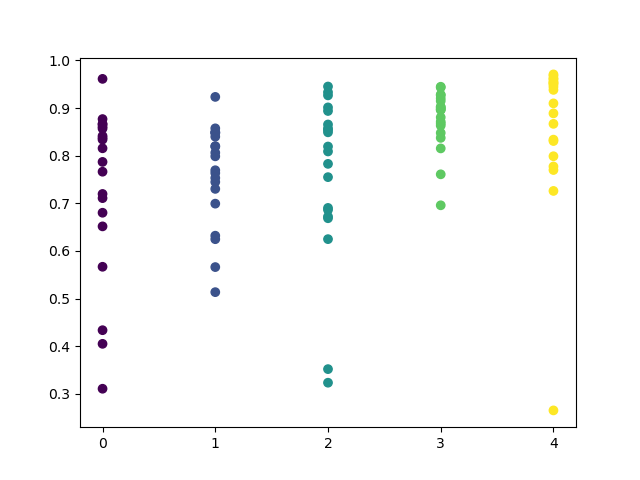
Vamos a entrenar el modelo de control para el jueves, y comprobar así el resultado. Este es el aspecto del ciclo de entrenamiento (para aquellos que no han leído los artículos anteriores).

hours = [3]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=5, max=25, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)

# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
    n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])


# iterative learning
res = []
for i in range(10):
    res.append(brute_force(10000, gmm))
    print('Iteration: ', i, 'R^2: ', res[-1][0])

# test best model
res.sort()
test_model(res[-1])

El resultado es algo peor que al utilizar una duración fija para las transacciones. 

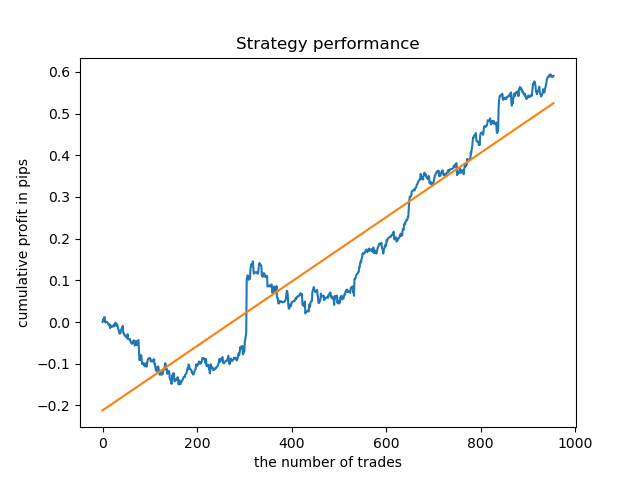
Obviamente, es importante el parámetro de frecuencia (horizonte) de las transacciones comerciales en periodos específicos. Sería interesante descifrar estos valores y ver cómo influyen en el resultado.

Valoración de la influencia de la duración de las transacciones sobre la calidad de los modelos.

Por analogía con la función de análisis exploratorio, usando el criterio (filtro) seleccionado, podemos escribir una función auxiliar que evaluará el rendimiento del modelo dependiendo de la duración de las transacciones. Vamos a suponer que podemos hacer fija la duración de las transacciones en un intervalo de 1 a 50 barras (o cualquier otro intervalo); la función se verá así.

def deals_frequency_analyzer():
    freq = [x for x in range(1, 50)]
    result = pd.DataFrame()
    for _h in freq:
        pr = get_prices(START_DATE, STOP_DATE)
        pr = add_labels(pr, min=_h, max=_h, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 5
        for i in range(iterations):
            res.append(brute_force(10000, gmm))
            print('Iteration: ', i, 'R^2: ', res[-1][0], ' deal lifetime = ', _h)
        
        r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h))
        result = result.append(r)

    plt.scatter(result.index, result, c = result.index)
    plt.xticks(np.arange(0, len(freq)+1, 1))
    plt.title("Performance by deals lifetime")
    plt.xlabel("deals frequency")
    plt.ylabel("R^2 estimation")
    plt.show()
    return result

La lista Freq contiene la duración de las transacciones iteradas. Hemos implementado la iteración así para la hora 5 de la pareja de divisas GBPUSD. Veamos el resultado.

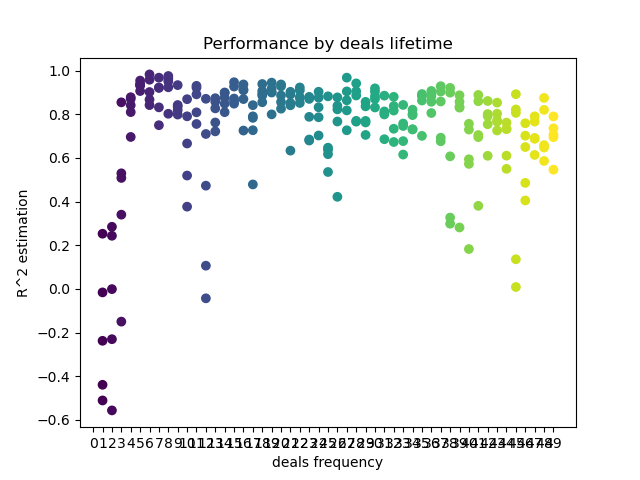
En el eje X, se muestra en barras la frecuencia de las transacciones, o más bien, su duración. En el eje Y, se encuentra la valoración R^2 para cada una de las pasadas. Podemos ver claramente que las transacciones demasiado cortas de 0-5 barras influyen negativamente en el rendimiento del modelo, mientras que el rango 15-23 resulta óptimo. Un aumento en la duración de las transacciones por encima de las 30 barras comienza a empeorar el resultado. Hay un pequeño clúster cuyas transacciones tienen una duración de 6-9 barras, para el que las valoraciones son máximas. Vamos a intentar entrenar los modelos con estas duraciones y comparar los resultados con otros grupos.

Hemos seleccionado una duración de 8 barras; el modelo ha pasado la prueba para dicha duración desde 2013, pero la curva de balance no es tan suave como querríamos.

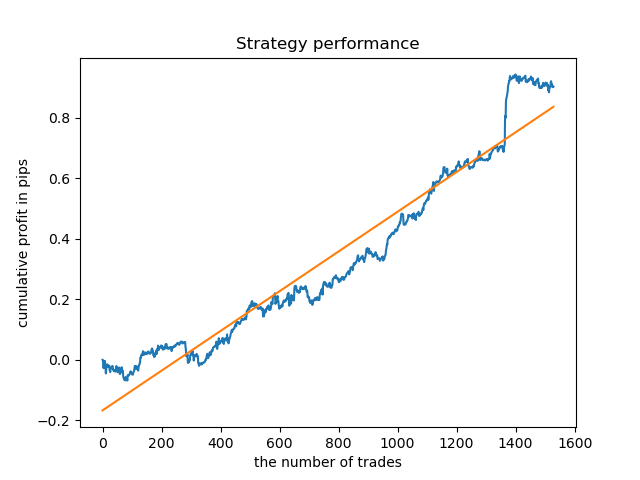
Para una duración del clúster más "concentrada", el gráfico tiene muy buen aspecto desde 2015; no obstante, el modelo muestra malos resultados en un segmento anterior de la historia.

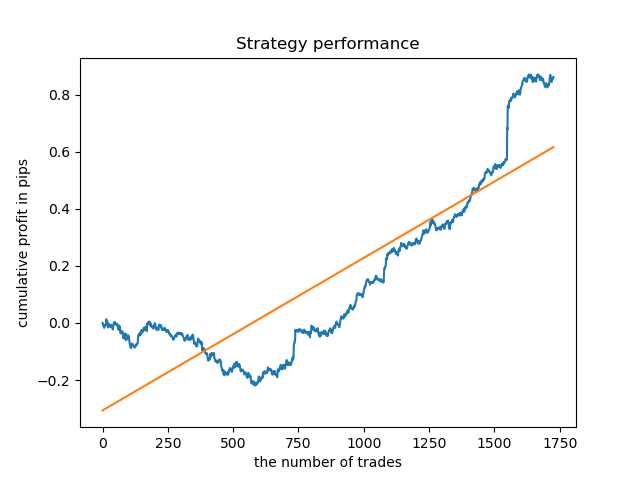
Al finalizar, hemos elegido el rango de los mejores clústeres 15-23, reentrenando el modelo varias veces (ya que el muestreo de la duración de las transacciones es aleatorio). 

pr = add_labels(pr, min=15, max=23, filter=time_filter)

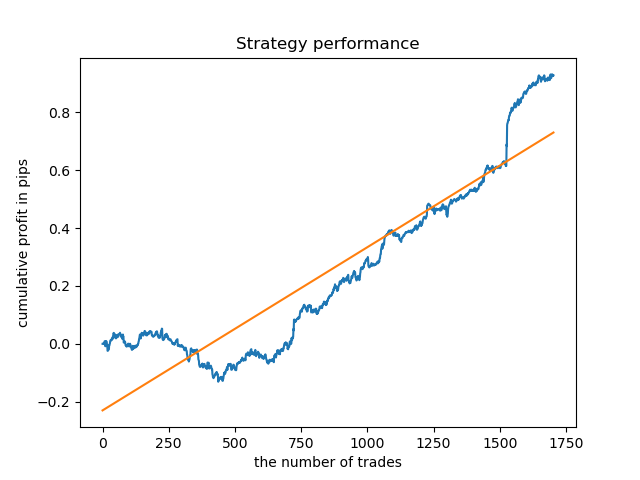
De media y con tales patrones, el modelo se niega a vivir con datos anteriores a 2015, lo cual se debe a algunos cambios fundamentales acaecidos en la estructura del mercado. Para analizar esta situación, necesitaríamos un estudio aparte bastante voluminoso. Una vez hemos seleccionado el modelo y demostrado su estabilidad en un determinado intervalo de tiempo, podemos implementar el entrenamiento en todo el intervalo (incluida la muestra de prueba) y comenzar la producción del modelo.

Realizando comprobaciones con una historia más larga

Podríamos sentir interés por revisar el modelo con una historia más larga. Hemos entrenado el modelo con datos desde 2000 y lo hemos puesto a prueba en un periodo que abarca desde 1990. En un área tan larga de la historia, los patrones se detectan con cierta debilidad, lo cual se refleja en una curva de balance desigual, aunque el resultado sigue siendo positivo.

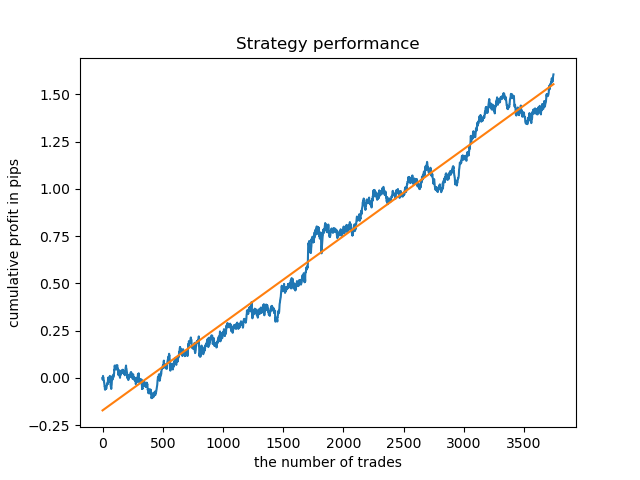
Conclusión

El artículo ofrece una poderosa herramienta para encontrar patrones estacionales y crear sistemas comerciales. Podemos realizar análisis para diferentes instrumentos (no necesariamente de fórex) y diferentes marcos temporales, y también con diferentes filtros (no necesariamente temporales). El espectro de aplicación de este enfoque resulta tan amplio que necesitaríamos multitud de pruebas con diferentes filtros para descubrir sus capacidades al completo. Después de realizar análisis, podemos componer un robot comercial listo para usar gracias a la función de exportación de modelos propuesta en artículos anteriores.