
Introducción a la teoría de la Lógica difusa
Introducción
La teoría matemática de los conjuntos difusos (fuzzy sets) y la misma lógica difusa (fuzzy logic) toma su inicio desde 1965. Su fundador es el profesor Lotfi Zadeh de la universidad de Berkeley. Precisamente él acuñó estos dos conceptos en su artículo “Fuzzy Sets”, en la revista Information and Control. Este aparato matemático ha permitido introducir en una ciencia exacta, como las matemáticas, los conceptos difusos (borrosos) que opera cualquier persona, y ha sentado las bases de unos métodos absolutamente nuevos de solucionar los problemas a base de las técnicas de Soft computing. Con un uso correcto, todas estas innovaciones pueden facilitar considerablemente el proceso de solución de problemas de clasificación, creación de los sistemas expertos y construcción de redes neuronales.
Sin embargo, la aplicación práctica de la lógica difusa no se limita con eso. En realidad, este aparato matemático ha obtenido su mayor propagación en la teoría de gestión automática. Precisamente con ese hecho se puede vincular la aparición de otro concepto nuevo — modelo difuso. Un modelo difuso es un caso particular del modelo matemático.
1. Teoría de conjuntos difusos y lógica difusa
En cierto modo, la nueva teoría de Lotfi Zadeh extiende los límites habituales de la lógica matemática y teoría de conjuntos. La lógica matemática es capaz de trabajar sólo con los datos estrictamente formalizados, y la pertenencia del objeto a uno u otro conjunto se determina sólo con dos conceptos, es decir el propio concepto “pertenencia” es un valor discreto que puede adquirir dos significados:
- “1” — si el objeto pertenece a uno u otro conjunto;
- “0” — si no pertenece.
En su teoría de conjuntos difusos, Lotfi Zadeh se ha apartado del concepto discreto de la “pertenencia” y ha introducido uno nuevo — “grado de pertenencia”, y los “conjuntos” habituales han sido sustituidos por los “conjuntos difusos”.
1.1. Términos principales y definiciones
Definición 1. Al conjunto difuso (fuzzy set) ![]() sobre un conjunto universal
sobre un conjunto universal ![]() se le llama un total de pares
se le llama un total de pares ![]() , donde
, donde ![]() es el grado de pertenencia del elemento
es el grado de pertenencia del elemento ![]() al conjunto difuso.
al conjunto difuso.
Definición 2. Grado de pertenencia es un número del rango [0, 1]. Cuanto más alto sea el grado de pertenencia, en mayor medida va a corresponder el elemento del conjunto universal a las propiedades de este conjunto difuso. Es decir, si el grado de pertenencia es igual a 0, este elemento no corresponde al conjunto en absoluto, y si es igual a 1, al revés, se puede decir que corresponde totalmente. Estos dos casos son extremos, y a falta de otras opciones representarían un conjunto usual. La presencia de todas las demás variantes es la diferencia clave de un conjunto difuso.
Definición 3. La función de pertenencia (membership function) es la función que permite calcular el grado de pertenencia de un elemento arbitrario del conjunto universal al conjunto difuso. Por consiguiente, el área de los valores de la función de pertenencia debe pertenecer al rango [0, 1]. En mayoría de los casos, la función de pertenencia es una función continua monótona.
Definición 4. A la variable lingüística (borrosa) (linguistic variable) se le llama una variable cuyos valores pueden ser palabras o combinaciones de palabras de un idioma natural o artificial. Precisamente de las variables lingüísticas se componen los conjuntos difusos. Cuando se define un conjunto difuso, el número y el carácter de las variables difusas es subjetivo para cada problema particular.
Definición 5. El conjunto de términos (term set) es un conjunto de todos los valores posibles que una variable lingüística puede recibir.
Definición 6. El término (term) es cualquier elemento del term set. En la teoría de conjuntos difusos, el term se formaliza por un conjunto difuso mediante la función de pertenencia. La función de pertenencia para cada término es individual, y a menudo única. Existen distintos métodos de construcción de estas funciones: directos, indirectos y métodos de frecuencias relativas. A menudo se basan en los puntos típicos de la función de pertenencia o datos empíricos del experto en este campo objetual.
Ejemplo:
Vamos a definir una variable lingüística con el nombre “Edad”. Por definición, la “Edad” es un período, etapa del desarrollo y crecimiento de una persona, animal o planta. El valor mínimo de esta variable es igual a 0, es decir, la persona ni siquiera ha cumplido un año. Como valor máximo tomaremos 80. Dependiendo de la edad concreta de la persona, podemos evaluar como: “recién nacido”, “niño”, “joven”, “edad media”, “viejo”, “edad madura”, etc. Esta lista puede incluir una cantidad bastante grande de los elementos. Será el term set para nuestra variable lingüística, y sus elementos serán los terms.
En la imagen de abajo se muestra un ejemplo de la variable difusa “Edad” para la cual hemos establecido un term set compuesto de tres terms. “Niño”, “Edad media”, “Viejo”. Cada de estos terms tiene su función de pertenencia.
Vamos a considerar el caso cuando la edad de la persona es igual a 30 años, lo que en la imagen va a corresponder a la línea perpendicular trazada del punto (30, 0). Esta recta va a cruzar las tres funciones de pertenencia en los siguientes puntos:
- (30, 0) — punto de intersección del gráfico “Edad de 30 años” y gráfico “Viejo”.
- (30, 0,29) — punto de intersección del gráfico “Edad de 30 años” y gráfico “Edad media”.
- (30, 0,027) — punto de intersección del gráfico “Edad de 30 años” y gráfico “Niño”.
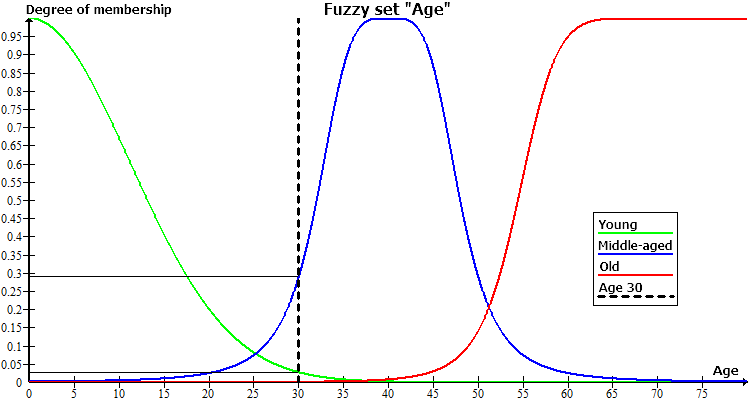
Basándose en las coordenadas de estos tres puntos podemos deducir que a una persona de 30 años de ninguna manera se puede llamarla vieja, y si hay que eligir entre niño y la edad media, prevalece la segunda opción. El grado de pertenencia al term “Edad media” es igual a 0,29 lo que es bastante poco. En realidad, para una persona de 30 años valdría mucho mejor el term, por ejemplo, “Joven”.
Definición 7. La defuzzificación (defuzzification) es el proceso de transformación de un conjunto difuso en un valor nítido. Actualmente, hay más de veinte métodos, y sus resultados pueden variarse considerablemente. Cabe destacar que los mejores resultados da la defuzzificación según el método del centro de gravedad (center of gravity).
1.2. Lógica difusa
La lógica difusa es la generalización de la lógica tradicional de Aristóteles para el caso cuando la veracidad se considera como una variable lingüística. Igual que en la lógica clásica, la lógica difusa tiene determinadas sus operaciones lógicas difusas con los conjuntos difusos. Para los conjuntos difusos existen las mismas operaciones que se utilizan en los conjuntos usuales, los único que su cálculo es más complicado. Cabe mencionar que la composición de los conjuntos difusos es un conjunto difuso.
Las particularidades principales de la lógica difusa, que la diferencian de la clásica, son la aproximación máxima a la representación de la realidad y alto nivel de subjetividad, a causa de que pueden surgir errores considerables en los resultados de los cálculos al usarla.
Un modelo difuso es un modelo matemático cuyos cálculos se basan en la lógica difusa. Se acuden a la construcción de estos modelos cuando el objeto de investigación tiene una débil formalización, y su descripción matemática nítida es muy compleja o simplemente desconocida. La calidad de los valores de salida de estos modelos (error del modelo) depende exclusivamente del experto que diseñaba y ajustaba el modelo. Para minimizar el error, la mejor opción será el diseño de un modelo máximamente completo y exhaustivo y su posterior ajuste a través de los medios del aprendizaje automático basándose en una importante selección didáctica.
El proceso de construcción del modelo puede ser dividido en tres fases principales:
- Definición de los parámetros de entrada y de salida del modelo.
- Construcción de la base de conocimiento.
- Elección de uno de los métodos de la inferencia lógica difusa.
La primera fase influye directamente en las dos siguientes determinando el futuro funcionamiento del modelo. La base de conocimiento, llamada también la base de reglas, es un conjunto de reglas difusas del tipo “si..., entonces”, que determinan la interacción entre las entradas y salidas del objeto investigado. El número de reglas dentro del sistema no está limitado y también se determina por el experto. El formato general de las reglas difusas es el siguiente:
Si condición de la regla, entonces conclusión de la regla.
La condición de la regla caracteriza el estado actual del objeto, y la conclusión- de qué manera esta condición va a influir sobre el objeto. No se puede destacar la vista general de las condiciones y conclusiones, puesto que se determinan por la inferencia lógica difusa.
Cada regla tiene su peso en el sistema. Este parámetro caracteriza la importancia de la regla en el modelo. Los coeficientes del peso se asignan a la regla dentro del rango [0, 1]. En muchos ejemplos de los modelos difusos que se puede encontrar en la literatura, estos pesos no se especifican, pero eso no significa que no existen. En realidad, para cada regla de la base en este caso el peso es fijo y es igual a 1. Las condiciones y las conclusiones para cada regla pueden ser de dos tipos:
- simple - tiene una variable difusa;
- compuesta - tiene varias variables difusas.
Dependiendo de la base de conocimiento creada, para el modelo se determina el sistema de la inferencia lógica difusa. La inferencia lógica difusa es la obtención de una conclusión en forma de un conjunto difuso correspondiente a los valores actuales de las entradas, usando la base difusa de conocimiento y operaciones difusas. Mamdani y Sugeno son dos tipos principales de la inferencia lógica difusa.
1.3. Inferencia lógica difusa tipo Mamdani
La inferencia lógica difusa según el algoritmo Mamdani se ejecuta usando la base difusa de conocimiento:
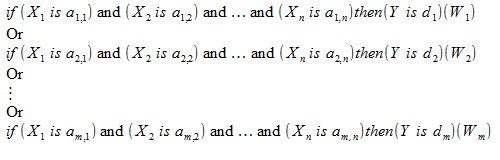
Los valores de la variable de entrada y de salida están establecidos con los conjuntos difusos.
Podemos escribir esta base de la siguiente manera:
![]()
donde:
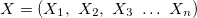 — vector de las variables de entrada;
— vector de las variables de entrada;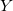 — variable de salida;
— variable de salida;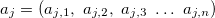 — vector de los valores de las variables de entrada en la j-ésima regla, j=0,1,2...m;
— vector de los valores de las variables de entrada en la j-ésima regla, j=0,1,2...m;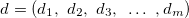 — vector de los valores de la variable de salida;
— vector de los valores de la variable de salida;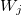 — peso de la j-ésima regla, j=0,1,2...m.
— peso de la j-ésima regla, j=0,1,2...m.
Introducimos un nuevo símbolo: ![]() — función de pertenencia de la variable difusa de entrada o de salida v al term difuso t.
— función de pertenencia de la variable difusa de entrada o de salida v al term difuso t.
El grado de pertenencia del vector de entrada a los terms difusos ![]() de la base de conocimiento se calcula de la siguiente manera:
de la base de conocimiento se calcula de la siguiente manera:
![]() — esta función va a caracterizar el resultado del trabajo de la j-esima regla de la base de conocimiento;
— esta función va a caracterizar el resultado del trabajo de la j-esima regla de la base de conocimiento;
donde ![]() — operación de la s-norma (t-norma), es decir, del conjunto de implementaciones de las operaciones lógicas OR (AND). Las implementaciones más frecuentes son las siguientes: para la operación OR es la búsqueda del máximo y para la operación AND es la búsqueda del mínimo.
— operación de la s-norma (t-norma), es decir, del conjunto de implementaciones de las operaciones lógicas OR (AND). Las implementaciones más frecuentes son las siguientes: para la operación OR es la búsqueda del máximo y para la operación AND es la búsqueda del mínimo.
Después de encontrar ![]() para
para ![]() , obtenemos m nuevas funciones de pertenencia que en total van a formar un nuevo conjunto difuso (lo marcamos como como
, obtenemos m nuevas funciones de pertenencia que en total van a formar un nuevo conjunto difuso (lo marcamos como como ![]() ) correspondiente al vector de entrada
) correspondiente al vector de entrada ![]() .
.
![]()
La particularidad de este conjunto difuso consiste en que el conjunto universal para él es el term-conjunto de la variable de salida ![]() .
.
A continuación, hay que hacer lo siguiente:
- “cortar” las funciones de pertenencia
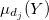 en el nivel
en el nivel 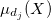 ;
; - combinar los conjuntos difusos obtenidos.
En otras palabras, realizar la implicación material y la agregación de las condiciones. La implicación material se modela usando dos métodos: la búsqueda del mínimo o del producto de los conjuntos, la agregación- la búsqueda del máximo o de la suma de los conjuntos.
Después de eso, obtenemos el conjunto difuso resultante cuya defuzzificación nos dará la salida exacta del sistema.
1.4. Inferencia lógica difusa tipo Sugeno
La inferencia lógica difusa según el algoritmo Sugeno se ejecuta usando la base difusa de conocimiento:
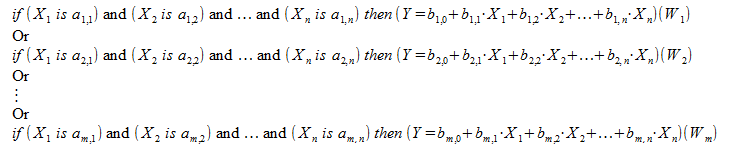
La base de conocimiento Seguno es igual a la base de conocimiento Mamdani a excepción de las conclusiones de las reglas ![]() que no se establecen con los terms difusos, sino con la función lineal de las entradas:
que no se establecen con los terms difusos, sino con la función lineal de las entradas:
![]()
Las reglas en la base de conocimiento Seguno son una especie de conmutadores de una ley lineal “entradas - salidas” a otro, también lineal. Los límites de las subzonas son borrosos, por tanto, varias leyes lineales pueden ejecutarse simultáneamente, pero con potencias diferentes.
Podemos escribir esta base de la siguiente manera:
![]()
donde:
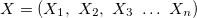 — vector de las variables de entrada.
— vector de las variables de entrada.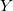 — variable de salida.
— variable de salida.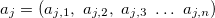 — vector de los valores de las variables de entrada en la j-ésima regla, j=0,1,2...m.
— vector de los valores de las variables de entrada en la j-ésima regla, j=0,1,2...m.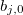 — coeficiente del miembro libre en la función lineal para el valor de salida en la j-ésima regla, j=0,1,2...m.
— coeficiente del miembro libre en la función lineal para el valor de salida en la j-ésima regla, j=0,1,2...m.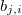 — coeficiente del i-ésimo miembro en la función lineal para el valor de salida en la j-ésima regla, j=0,1,2...m, i=0,1,2...n.
— coeficiente del i-ésimo miembro en la función lineal para el valor de salida en la j-ésima regla, j=0,1,2...m, i=0,1,2...n.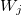 — peso de la j-ésima regla, j=0,1,2...m.
— peso de la j-ésima regla, j=0,1,2...m.
Introducimos un nuevo símbolo: ![]() — función de pertenencia de la variable difusa de entrada o de salida v al term difuso t.
— función de pertenencia de la variable difusa de entrada o de salida v al term difuso t.
El grado de pertenencia del vector de entrada a los terms difusos ![]() de la base de conocimiento se calcula de la siguiente manera:
de la base de conocimiento se calcula de la siguiente manera:
![]() — esta función va a caracterizar el resultado del trabajo de la j-esima regla de la base de conocimiento;
— esta función va a caracterizar el resultado del trabajo de la j-esima regla de la base de conocimiento;
donde ![]() — operación de la s-norma (t-norma), es decir, del conjunto de implementaciones de las operaciones lógicas OR (AND). En la inferencia lógica difusa de Seguno, se utilizan con la mayor frecuencia las siguientes implementaciones de las normas triangulares: OR probabilista como la s-norma y el producto como la t-norma.
— operación de la s-norma (t-norma), es decir, del conjunto de implementaciones de las operaciones lógicas OR (AND). En la inferencia lógica difusa de Seguno, se utilizan con la mayor frecuencia las siguientes implementaciones de las normas triangulares: OR probabilista como la s-norma y el producto como la t-norma.
Después de encontrar ![]() para
para ![]() , obtenemos m nuevas funciones de pertenencia que en total van a formar un nuevo conjunto difuso (lo marcamos como
, obtenemos m nuevas funciones de pertenencia que en total van a formar un nuevo conjunto difuso (lo marcamos como ![]() ) correspondiente al vector de entrada
) correspondiente al vector de entrada ![]() .
.
![]()
Nótese que a diferencia del resultado de la salida de Mamdani mostrado anteriormente, el conjunto difuso es un conjunto difuso habitual del primer orden. Se establece a base del conjunto de los valores nítidos. El valor resultante de la salida ![]() se determina como la superposición de las dependencias lineales ejecutadas en este punto
se determina como la superposición de las dependencias lineales ejecutadas en este punto ![]() del espacio factorial de n dimenciones. Para eso defuzzifica el conjunto difuso
del espacio factorial de n dimenciones. Para eso defuzzifica el conjunto difuso ![]() encontrando la media ponderada o la suma ponderada.
encontrando la media ponderada o la suma ponderada.
2. Biblioteca de la lógica difusa FuzzyNet
En la práctica, el desarrollo y el trabajo incluso con un modelo difuso simple es una tarea bastante complicada. Sin embargo, existen varios medios informáticos y bibliotecas que la facilitan considerablemente. Vamos a analizar el proceso de creación y trabajo de dos modelos difusos tomando del ejemplo los scripts textuales de la biblioteca FuzzyNet para MQL5.
2.1. Diseño de sistemas tipo Mamdani
El primer ejemplo es el script Tips_Sample_Mamdani.mq5 de la biblioteca FuzzyNet para MQL5. En él está implementado el modelo difuso para calcular la propina que al cliente del establecimiento es preferible dejar basándose en su evaluación de la calidad del servicio y de la comida. Este sistema tiene dos entradas lógicas difusas, una salida, base de conocimiento que incluye tres reglas y el sistema de inferencia lógica tipo Mamdani.
Los parámetros de entrada serán las variables difusas “comida” (food) y “servicio” (service), las dos variables se evalúan según la escala de 0 a 10 (son sus valores mínimos y máximos). La variable “comida” se compone de dos terms: “desabrida” (rancid), “deliciosa” (delicious). La variable “servicio” va a componerse de tres terms difusos: “malo” (poor), “bueno” (good), “excelente” (excellent).
En la salida obtendremos la variable difusa “propina” (tips). Determinaremos el rango de valores de la propina a dejar de 5 a 30% del importe de la cuenta y crearemos tres terms para esta variable: “pequeña” (cheap), “media” (average), “grande” (generous).
La base de conocimiento de este sistema tendrá tres reglas:
- Si (el servicio es malo) o (la comida es desabrida), la propina es pequeña.
- Si (el servicio es bueno), la propina es media.
- Si (el servicio es excelente) o (la comida es deliciosa), la propina es grande.
Ahora, teniendo la visión general del sistema, veremos el proceso de su diseño:
- Incluimos el archivo MamdaniFuzzySystem.mqh de la biblioteca FuzzyNet para MQL5:
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>Este archivo permite crear los sistemas tipo Mamdani y trabajar con ellos. - Ahora podemos crear un sistema vacío de Mamdani y luego ir llenándolo:
MamdaniFuzzySystem *fsTips=new MamdaniFuzzySystem(); - Creamos la primera variable de entrada “servicio”. Cuando se crean las variables difusas, como los parámetros para el constructor primero se indica el nombre de la variable en forma de la cadena, luego su valor mínimo y máximo.
FuzzyVariable *fvService=new FuzzyVariable("service",0,0,10,0);
- Insertamos en ella los terms difusos. El primer parámetro que recibe el constructor de los términos difusos será el nombre en forma de la cadena, el segundo será la función de pertenencia que le corresponde.
fvService.Terms().Add(new FuzzyTerm("poor", new TriangularMembershipFunction(-5,0, 0,0, 5,0))); fvService.Terms().Add(new FuzzyTerm("good", new TriangularMembershipFunction(0,0, 5,0, 10,0))); fvService.Terms().Add(new FuzzyTerm("excellent", new TriangularMembershipFunction(5,0, 10,0, 15,0)));
Las funciones de pertenencia en este ejemplo están representadas en forma de una función triangular para todos los terms. - Ahora añadimos la variable difusa ya hecha y formada en nuestro sistema:
fsTips.Input().Add(fvService);
- Implementamos de la misma manera la segunda entrada con la variable “comida”, lo único que los terms para esta variable van a tener la función de pertenencia trapezoidal.
FuzzyVariable *fvFood=new FuzzyVariable("food",0,0,10,0); fvFood.Terms().Add(new FuzzyTerm("rancid", new TrapezoidMembershipFunction(0,0, 0,0, 1,0, 3,0))); fvFood.Terms().Add(new FuzzyTerm("delicious", new TrapezoidMembershipFunction(7,0, 9,0, 10,0, 10,0))); fsTips.Input().Add(fvFood);
- Dado que el sistema tiene la inferencia lógica tipo Mamdani, sus valores de entrada y salida van a determinarse con los mismos métodos. Por eso creamos analógicamente la salida:
FuzzyVariable *fvTips=new FuzzyVariable("tips",0,0,30,0); fvTips.Terms().Add(new FuzzyTerm("cheap", new TriangularMembershipFunction(0,0, 5,0, 10,0))); fvTips.Terms().Add(new FuzzyTerm("average", new TriangularMembershipFunction(10,0, 15,0, 20,0))); fvTips.Terms().Add(new FuzzyTerm("generous", new TriangularMembershipFunction(20,0, 25,0, 30,0))); fsTips.Output().Add(fvTips);
- Vamos a crear las reglas difusas que en total van a representar la base de conocimiento de nuestro sistema. Para crear una regla, hay que llamar al método ParseRule del objeto que representa nuestro sistema, y pasarle como parámetro la representación string de la regla difusa:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is cheap)"); MamdaniFuzzyRule *rule2 = fsTips.ParseRule("if (service is good) then (tips is average)"); MamdaniFuzzyRule *rule3 = fsTips.ParseRule("if (service is excellent) or (food is delicious) then (tips is generous)");
La escritura de las reglas difusas está estrictamente tipificada y no admite el uso de las palabras no clave. Las palabras clave son las siguientes: "if", "then", "is", "and", "or", "not", "(" , ")", "slightly", "somewhat", "very", "extremely". Las últimas cuatro palabras clave son cuantificadores lingüísticos. Todos los nombres de las variables, terms y funciones que existen en su sistema también pertenecen a las palabras clave. Mediante los cuantificadores lingüísticos aumentan o, al revés, reducen la importancia de los terms difusos o de las funciones lineales Sugeno. Implementación de los cuantificadores lingüísticos:
- "slightly" — “apenas”, reemplaza el resultado de la condición por su raíz cúbica. Reduce considerablemente la importancia.
- "somewhat" — “en parte”, reemplaza el resultado de la condición por su raíz cuadrada. Reduce la importancia.
- "very" — “muy”, eleva el resultado de la condición a la potencia 2. Aumenta la importancia.
- "extremely" — “extremamente”, eleva el resultado de la condición a la potencia 3. Sube muchísimo la importancia.
- "slightly" — “apenas”, reemplaza el resultado de la condición por su raíz cúbica. Reduce considerablemente la importancia.
- Sólo nos queda añadir las reglas al sistema:
fsTips.Rules().Add(rule1); fsTips.Rules().Add(rule2); fsTips.Rules().Add(rule3);
Ahora tenemos un modelo listo para calcular la propina a base del sistema de la inferencia lógica difusa tipo Mamdani.
2.2. Diseño de sistemas tipo Sugeno
Como ejemplo de implementación del sistema Sugeno vamos a tomar el script que calcula la gestión necesaria del sistema del autocrucero (control de velocidad) del automóvil. Este script está descrito en el archivo Cruise_Control_Sample_Sugeno.mq5 de la biblioteca FuzzyNet para MQL5 siendo uno de los ejemplos de la aplicación de los modelos difusos para la solución de las tareas de gestión automática.
Precisamente para estas tareas unidimensionales la lógica difusa se aplica mayormente en los sistemas de control automático (SCA). El planteamiento de estas tareas aproximadamente es el siguiente: en un momento dado ![]() un cierto objeto se encuentra en el estado “A”, es necesario que en el tiempo
un cierto objeto se encuentra en el estado “A”, es necesario que en el tiempo ![]() pase al estado “B”. Para solucionar el problema de este tipo, el período de tiempo se divide en
pase al estado “B”. Para solucionar el problema de este tipo, el período de tiempo se divide en ![]() partes, se encuentra el paso de tiempo igual a
partes, se encuentra el paso de tiempo igual a ![]() , y luego SCA tiene que desarrollar el control en cada punto
, y luego SCA tiene que desarrollar el control en cada punto ![]() , donde i=0,1,2...n.
, donde i=0,1,2...n.
Diferentes controladores PID pueden cumplir con esta tarea, pero tienen una importante desventaja: no son capaces de desarrollar, digamos, el control “suave”. Es decir, si construimos el sistema del autocrucero del coche a base del controlador PID, al cambiar la velocidad este sistema nos llevará a la velocidad predefinida pero pueden surgir diferentes acelerones y empujones. El controlador difuso podrá cumplir con la tarea de una manera más suave desde el punto de vista del ser humano.
Es evidente que en la salida de nuestro controlador difuso estará el cambio necesario de la velocidad en forma de aceleración, y en la entrada estará el error y la primera derivada del error. El error es la desviación del estado actual respecto al deseado. En otras palabras, en la entrada del sistema van a llegar los siguientes datos:
- la diferencia entre la velocidad del coche en este momento y la velocidad establecida en el sistema del autocrucero;
- con qué rapidez esta diferencia se reduce (se aumenta).
Pues bien, el primer parámetro de entrada “error de velocidad” (SpeedError) va a recibir los valores de -20 a 20 km/h y tener tres terms: “más lento” (slower), “sin cambios” (zero), “más rápido” (faster). Los tres terms van a tener la función de pertenencia triangular. La segunda entrada es la “derivada del error de velocidad” (SpeedErrorDot) con el rango de -5 a 5 y los terms difusos “más lento” (slower), “sin cambios” (zero), “más rápido” (faster), también con la función de pertenencia triangular.
Puesto que nuestro modelo dispone del sistema de la inferencia lógica Sugeno, el valor de salida “aceleración” (Accelerate) no va a tener el valor máximo y mínimo, y en vez de los terms difusos habrá combinaciones lineales de las variables de entrada que también tendrán los nombres: “no cambiar” (zero), “aumentar” (faster), “reducir” (slower), “mantener” (func). Describimos estas cuatro combinaciones lineales. Para eso denominamos la variable SpeedError como ![]() , SpeedErrorDot como
, SpeedErrorDot como ![]() , y Accelerate como
, y Accelerate como ![]() , entonces obtendremos las ecuaciones siguientes:
, entonces obtendremos las ecuaciones siguientes:
- zero:
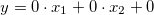 ;
; - faster:
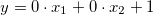 ;
; - slower:
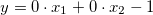 ;
; - func:
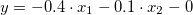 .
.
La base de conocimiento de este sistema tendrá nueve reglas:
- Si el (error se ha reducido) y la (derivada del error se ha reducido), entonces aumentar la aceleración.
- Si el (error se ha reducido) y la (derivada del error no se ha cambiado), entonces aumentar la aceleración.
- Si el (error se ha reducido) y la (derivada del error se ha aumentado), entonces no cambiar la aceleración.
- Si el (error no se ha cambiado) y la (derivada del error se ha reducido), entonces aumentar la aceleración.
- Si el (error no se ha cambiado) y la (derivada del error no se ha cambiado), entonces mantener la aceleración.
- Si el (error no se ha cambiado) y la (derivada del error se ha aumentado), entonces reducir la aceleración.
- Si el (error se ha aumentado) y la (derivada del error se ha reducido), entonces aumentar la aceleración.
- Si el (error se ha aumentado) y la (derivada del error no se ha cambiado), entonces reducir la aceleración.
- Si el (error se ha aumentado) y la (derivada del error se ha aumentado), entonces reducir la aceleración.
Veremos el proceso de la creación del sistema:
- Incluimos el archivo SugenoFuzzySystem.mqh de la biblioteca FuzzyNet para MQL5:
#include <Math\FuzzyNet\SugenoFuzzySystem.mqh>Este archivo permite crear los sistemas tipo Sugeno y trabajar con ellos. - Ahora podemos crear un sistema vacío de Sugeno y luego ir llenándolo:
SugenoFuzzySystem *fsCruiseControl=new SugenoFuzzySystem(); - Las variables de entrada para el sistema Sugeno se crean igual que para el sistema tipo Mamdani.
Creamos la variable “error de velocidad” y la insertamos en el sistema:
FuzzyVariable *fvSpeedError=new FuzzyVariable("SpeedError",-20.0,20.0); fvSpeedError.Terms().Add(new FuzzyTerm("slower",new TriangularMembershipFunction(-35.0,-20.0,-5.0))); fvSpeedError.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-15.0, -0.0, 15.0))); fvSpeedError.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(5.0, 20.0, 35.0)));
Creamos la variable “variación del error de velocidad” y la insertamos en el sistema:
FuzzyVariable *fvSpeedErrorDot=new FuzzyVariable("SpeedErrorDot",-5.0,5.0); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("slower", new TriangularMembershipFunction(-9.0, -5.0, -1.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-4.0, -0.0, 4.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(1.0, 5.0, 9.0)));
- Creamos la variable difusa tipo Sugeno que va a ser la salida del sistema. Al crear la variable difusa, el constructor recibe sólo un parámetro- su nombre. Luego se puede añadir las funciones lineales en ella, pero previamente hay que definir esta funciones, y para eso vamos a necesitar un array de coeficientes tipo double.
La formación de una función lineal se realiza de la siguiente manera: cada variable de entrada será la incógnita de la ecuación con el coeficiente obtenido del array de coeficientes. De esta manera, en el array los coeficientes tienen que ubicarse en el mismo orden en que han sido introducidas las variables de entrada. Así, a la primera variable de entrada le va a corresponder el coeficiente con el índice 0, a la segunda, con el índice 1, etc. Por esa razón, la longitud del array de coeficientes tiene que ser a 1 más o igual al número de las variables de entrada. Si las longitudes son iguales, el coeficiente del miembro libre será igual a cero, de lo contrario su valor será igual al último elemento del array.
Nuestro sistema tiene dos variables de entrada, por eso las longitudes de los arrays de coeficientes no pueden ser más de tres. Declaramos cuatro arrays, formamos a su base las funciones descritas antes y las agregamos en la variable difusa tipo Sugeno; y ésta a su vez se introduce en el sistema:SugenoVariable *svAccelerate=new SugenoVariable("Accelerate"); double coeff1[3]={0.0,0.0,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("zero",coeff1)); double coeff2[3]={0.0,0.0,1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("faster",coeff2)); double coeff3[3]={0.0,0.0,-1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("slower",coeff3)); double coeff4[3]={-0.04,-0.1,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("func",coeff4)); fsCruiseControl.Output().Add(svAccelerate);
- Igual que en el sistema Mamdani, creamos nueve reglas difusas:
SugenoFuzzyRule *rule1 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule2 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is zero) then (Accelerate is faster)"); SugenoFuzzyRule *rule3 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is faster) then (Accelerate is zero)"); SugenoFuzzyRule *rule4 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule5 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is zero) then (Accelerate is func)"); SugenoFuzzyRule *rule6 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is faster) then (Accelerate is slower)"); SugenoFuzzyRule *rule7 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule8 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is zero) then (Accelerate is slower)"); SugenoFuzzyRule *rule9 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is faster) then (Accelerate is slower)");
- Vamos a insertarlas en nuestro sistema:
fsCruiseControl.Rules().Add(rule1); fsCruiseControl.Rules().Add(rule2); fsCruiseControl.Rules().Add(rule3); fsCruiseControl.Rules().Add(rule4); fsCruiseControl.Rules().Add(rule5); fsCruiseControl.Rules().Add(rule6); fsCruiseControl.Rules().Add(rule7); fsCruiseControl.Rules().Add(rule8); fsCruiseControl.Rules().Add(rule9);
2.3. Cálculo de sistemas tipo Mamdani y Sugeno
A la entrada de un sistema difuso tiene que pasarse una variable difusa y su valor. Como hemos dicho antes, las variables difusas reciben los valores de su term-conjunto. Por consiguiente, el resultado del cálculo del sistema va a depender de las funciones de pertenencia que corresponden a los terms pasados a la entrada y pertenecientes a las variables difusas de entrada. No obstante, en la mayoría de los casos, a la entrada del sistema se envían las variables difusas en forma de simples valores numéricos, y en la salida se espera obtener un resultado preciso de la misma forma. En este caso resulta que el term difuso no tiene la declaración explícita y su función de pertenencia se representa como la función de pertenencia constante. Precisamente con este caso particular trabajan los sistemas escritos con el uso de la biblioteca FuzzyNet.
¿Y qué exactamente hay que pasar a la entrada del sistema y en qué forma obtendremos el resultado del sistema?
El número de las variables de entrada para los sistemas difusos no está limitado. Cada entrada tiene que recibir obligatoriamente algunos valores, por tanto tenemos que disponer de la lista en la que vamos a almacenar los valores para cada entrada. Los elementos de esta lista tienen que ser los objetos complejos con dos campos: el primero para la variable difusa, el segundo para el valor numérico tipo double. En el archivo Dictionary.mqh de la biblioteca FuzzyNet на MQL5 está implementada la clase Dictionary_Obj_Double que permite crear estos objetos.
Vamos a formar la lista de entrada para nuestro sistema tipo Mamdani:
CList *in=new CList; Dictionary_Obj_Double *p_od_Service=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_Food=new Dictionary_Obj_Double; p_od_Service.SetAll(fvService, Service); p_od_Food.SetAll(fvFood, Food); in.Add(p_od_Service); in.Add(p_od_Food);
Aquí Service y Food son dos parámetros de entrada tipo double.
En los ejemplos descritos anteriormente cada uno de ambos sistemas, tanto Mamdani como Sugeno, tiene sólo una salida. Aunque en caso general, igual que con las entradas, no hay ninguna limitación en cuanto a su número. La estructura de la entrada y la salida es absolutamente igual.
Salida para el sistema tipo Mamdani:
CList *result=new CList; Dictionary_Obj_Double *p_od_Tips=new Dictionary_Obj_Double;
Ahora llamamos para cada sistema la función Calculate que recibe un parámetro- la lista de entradas, y devuelve la lista de salidas. Por el índice 0 obtenemos de esta lista los valores de la salida del sistema que está representada como el objeto de la clase Dictionary_Obj_Double. Usando los métodos Key y Value para este objeto, se puede obtener la variable y su resultado, respectivamente.
Vamos a ejecutar el cálculo para el sistema Mamdani y mostrar en la pantalla el número obtenido con la variable difusa de salida fvTips:
result=fsTips.Calculate(in); p_od_Tips=result.GetNodeAtIndex(0); Alert("Tips, %: ",p_od_Tips.Value());
Hagamos lo mismo con el sistema Sugeno:
CList *in=new CList; Dictionary_Obj_Double *p_od_Error=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_ErrorDot=new Dictionary_Obj_Double; p_od_Error.SetAll(fvSpeedError,Speed_Error); p_od_ErrorDot.SetAll(fvSpeedErrorDot,Speed_ErrorDot); in.Add(p_od_Error); in.Add(p_od_ErrorDot); CList *result=new CList; Dictionary_Obj_Double *p_od_Accelerate=new Dictionary_Obj_Double; result=fsCruiseControl.Calculate(in); p_od_Accelerate=result.GetNodeAtIndex(0); Alert("Accelerate, %: ",p_od_Accelerate.Value()*100);
Conclusión
Si descarga la biblioteca FuzzyNet para MQL5 o MQL4, podrá analizar detalladamente los scripts descritos anteriormente, así como crear su modelo difuso. Es importante comprender que la construcción de los modelos difusos “de combate” no es un trabajo sencillo, incluso con el uso de algunas bibliotecas auxiliares. Es más, cada modelo hecho requiere obligatoriamente una comprobación y configuración punto por punto.
Lista de literatura y referencias
- http://www.bindichen.co.uk/post/AI/mamdani-fuzzy-model.html — Mamdani fuzzy model.
- http://www.bindichen.co.uk/post/AI/takagi-sugeno-fuzzy-model.html — Sugeno fuzzy model.
- http://reference.wolfram.com/applications/fuzzylogic/DemonstrationNotebooks/5.html — fuzzy logic control.
- http://plato.stanford.edu/entries/logic-fuzzy — Fuzzy Logic Introduction.
- Lotfi A. Zadeh. Fuzzy sets and their applications
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1991
 Recetas MQL5 - órdenes ОСО
Recetas MQL5 - órdenes ОСО
 Barras sintéticas - una nueva dimensión de la visualización de información gráfica de los precios
Barras sintéticas - una nueva dimensión de la visualización de información gráfica de los precios
 Programamos los modos de funcionamiento del Asesor Experto usando la programación orientada a objetos
Programamos los modos de funcionamiento del Asesor Experto usando la programación orientada a objetos
 Sistema de Trading Mecánico "Horquilla de Chuvashov"
Sistema de Trading Mecánico "Horquilla de Chuvashov"
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso