
ファジーロジックの概要
イントロダクション
数学的なファジー集合理論とファジーロジック自体は1965年に始まりました。その基礎を作ったのは、最初に情報制御ジャーナルに「ファジー集合」の概念を導入したバークレー大学のロトフィザデー教授でした。この数学的な方法は、数学のような厳密な分野でファジィ概念を導入することができ、ソフトコンピューティングに基づいて、問題解決の根本的に新しい方法論を築きました。適切に利用すると、分類問題を解決するエキスパートシステムを作成するだけでなく、ニューラルネットワークを構築するプロセスを容易にします。
しかし、ファジー理論の実用化は、そこでとどまることはなく、この数学的手法は主に自動制御理論で使用されるようになりました。これは、さらに別の新しい概念にリンクさせることができます - つまり、数学モデルにおけるファジーモデルの場合です。
1。ファジー集合とファジー論理の背後にある理論
特定の方法で、ロトフィザデーの新理論は、数学的な論理と馴染み深い集合論の境界を拡張します。数学的なロジックは厳密な定式化データで動作可能であり、特定のセットのオブジェクトのメンバシップは、2つの概念によってのみ規定され、従って、"メンバシップ"は、2つの意味を有することができる個別の値を持ちます。
- "1" - オブジェクトがセットに属している場合。
- "0" - オブジェクトがセットに属していない場合。
従来の「ファジー集合」の代わりに「セット」という用語を使用するのに対し、ロトフィザデーのファジィ集合論では、「メンバーシップ」の離散的な概念からシフトし、"帰属度"という新しい用語を導入しました。
1.1。基本的な用語と定義
定義1。ファジー集合![]() ユニバーサルセットの
ユニバーサルセットの![]() ペア
ペア![]() は、
は、![]() 示している要素のメンバーシップ度
示している要素のメンバーシップ度![]() のファジーのセットです。
のファジーのセットです。
定義2。メンバシップ度は、[0,1]の範囲にある。メンバーシップ度が高いと、全体集合のより多くの要素はファジィ集合の特性に対応します。よって、メンバーシップが0の場合は、与えられた要素がセットに対応しておらず、反対に、メンバーシップ度が1の場合完全に対応します。これら2つのケースが両極であり、他のオプションなしでは通常のセットとなります。他のすべてのオプションは、ファジー集合の重要な差です。
定義3。メンバーシップ関数は、ファジー集合にユニバーサルセットのランダムな要素のメンバーシップ度を計算する機能です。したがって、メンバーシップ関数の領域は、[0,1]の範囲内にあります。ほとんどの場合、メンバーシップ関数は、連続的な単調関数です。
定義4。言語変数は、値が単語または単語の組み合わせの人工言語の変数です。特に、ファジーセットは言語変数から構成されています。ファジー集合を定義するとき、ファジー変数の量と性質は、個別のタスクです。
定義5。用語セットは、言語変数が受信可能な全ての値のセットです。
定義6。用語は、用語セットの任意の要素になることができます。ファジー集合論では、用語がメンバーシップ関数を介したファジー集合によって定式化されています。各用語のためのメンバーシップ関数は、非常にユニークです。これらの機能を構築する方法:直接法、間接法及び相対頻度。これらは多くの場合、メンバーシップ関数と、この分野の専門家の経験的証拠に基づいています。
例:
それでは、「年齢」と呼ばれる言語変数を定義してみましょう。定義において、「年齢」の区分、つまり、人間、動物、植物が第一歩です。この変数の最小値は0です。最大値は80です。「新生児」、「若者」、「中年」、「高齢」、「老齢」など:人の年齢に応じて、次のような評価を与えることができます。このリストは、かなり大きな数を収容することができます。言語変数の用語セットになり、その要素は用語になります。
下の図は、設定に3つの項があるファジー変数、「年齢」の一例を示しています。「若者」、「中年」、「高齢」において、これらの用語のそれぞれは、独自のメンバーシップ関数を有しています。
ある人が30歳のとき、数字上の点から下ろした垂線と対応させます。(30、0)。この線は、3つのメンバーシップ関数とクロスすることになります。
- (30、0) - グラフ「30歳」とグラフ「高齢」の交点。
- (30、0.29) - グラフ"30歳"とグラフ「中年」の交点。
- (30、0.027) - グラフ「30歳」とグラフ「若者」の交点
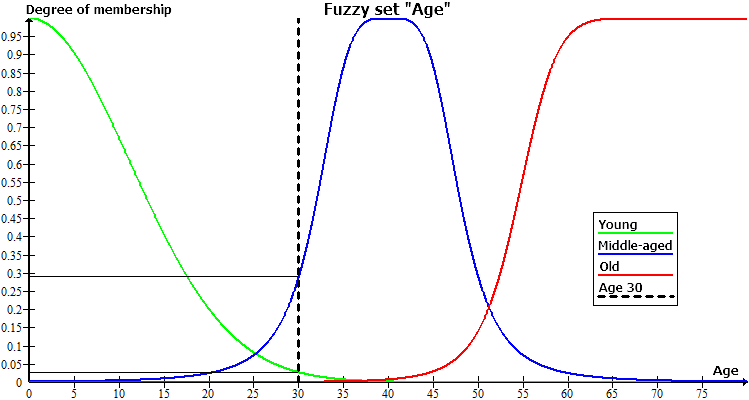
これら3点の座標から、我々は30歳の男性が高齢と呼べることができないという結論することができ、そして若者や中年の観点から選択する場合は、2番目となるでしょう。用語へのメンバーシップ度は「中年」がかなり小さく0.29、実際には、30歳の男性には用語「若者」が、フィットするでしょう。
定義7。非ファジー化は、特定の番号にファジー集合を変換する手順です。現在のところ20以上の方法があり、その結果は、互いに大きく異なっています。これまでの非ファジィ化法の最良の結果は、重心を利用しています。
1.2。ファジーロジック
ファジーロジックは、言語変数として記述されている伝統的なアリストテレスロジックのシンセサイズです。古典論理に相当するファジーロジックは、定義されたファジー集合上で、独自のファジー論理演算を有します。通常のセット同様に、ファジーセットのためのオペレーションがありますが、計算がはるかに難しいという点があります。また、ファジー集合の組成はファジー集合として構成していることに注意してください。
古典論理から離れて行うファジーロジックは、大きな誤差につながる可能性があります。
ファジーモデル - は、その計算がファジーロジックに基づいて行われる数学的モデルです。このようなモデルの構築は、研究対象に弱い形式性があり、厳密に計算しようとすると複雑になりすぎてしまう場合に有効です。これらのモデルの出力値(エラーモデル)の品質は、直接的にこのモデルを設定した専門家に依存します。誤差を最小化するための最良の方法は、最も完全かつ包括的なモデルを描き、その後、機械学習でそれを調整することです。
モデル構築のプロセスは、次の3つの段階に分けることができます。
- モデルの入出力特性の定義。
- 知識ベースを構築。
- ファジー推論の方法を選択。
第一段階では、その結果が2に影響を与え、モデルの将来を決定します。ルール・ベースなどと呼ばれることもある知識ベースは、ファジィルールタイプのセットです。:"ただし"、入力と出力の関係性を定義する場合。システム内のルールの数は制限されず、また、専門家によって決定されます。次のように、ファジィルールの一般形式はなります。
ルールの条件 の場合、ルールの結論
ルール条件は、現在のオブジェクトの状態を記述し、ルール結論は、この条件がオブジェクトにどのような影響を与えるかを記述します。ファジー推論によって決定されるので、条件と結論の一般的な見解は選択されてはいけません。
システム内の各ルールは、その重みを有し、この特性は、モデル内のルールの重要性を定義します。重み係数は、[0,1]範囲内のルールに割り当てられています。関連文献のファジーモデルの例では、重み付けデータが指定されていないが、それは存在していない訳ではありません。実際には、ルール・ベースから各ルールのような場合、重み付けが固定され、1に等しくされます。各ルールの用語や結論の2つのタイプが存在します。
- シンプル - 1ファジィ変数を含む。
- コンプレックス - 複数のファジィ変数を含む。
作成された知識ベースに応じて、ファジー推論のシステムはモデルが決定されます。ファジーロジカル推論は、知識ベースとファジー演算を用いた、インプットの現在値に応じたファジー集合の形態です。ファジー推論の2つの主要なタイプはマムダニメソッドとスゲノメソッドです。
1.3。マムダニ型ファジー推論
マムダニアルゴリズムによると、ファジー推論はファジィ知識ベースを使って実行されます。
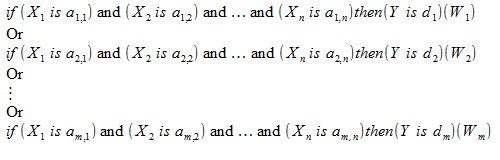
知識ベースにおける入力変数と出力変数の値は、ファジー集合によって設定されます。
この知識ベースは、次のように書くこともできます。
![]()
ここで、以下のことが適用されます
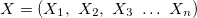 - 入力変数のベクトル;
- 入力変数のベクトル;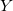 - 出力変数;
- 出力変数;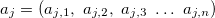 — j-番目 ルールの入力変数のベクトル, j = 0,1,2 ... m;
— j-番目 ルールの入力変数のベクトル, j = 0,1,2 ... m;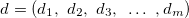 - 出力変数の値のベクトル;
- 出力変数の値のベクトル;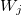 — j番目のルールの重み付け, j = 0,1,2 ... m.
— j番目のルールの重み付け, j = 0,1,2 ... m.
それでは、新しい方法をご紹介しましょう:![]() - ファジィ入力または出力変数 v のメンバーシップ関数t。
- ファジィ入力または出力変数 v のメンバーシップ関数t。
ファジータームの入力ベクトルのメンバーシップ度![]() は、次のように知識ベースから計算されます。:
は、次のように知識ベースから計算されます。:
![]() - この関数は、知識ベースから J番目のルールを特徴付けます。
- この関数は、知識ベースから J番目のルールを特徴付けます。
ただし、![]() - s-ノルム(T-ノルム)演算、すなわちOR(AND)論理演算の実装。次の実装が、最も頻繁に使用されています。ORは - 最大値の検索を - ANDは最小値を求めます。
- s-ノルム(T-ノルム)演算、すなわちOR(AND)論理演算の実装。次の実装が、最も頻繁に使用されています。ORは - 最大値の検索を - ANDは最小値を求めます。
![]() for
for![]() を見つけた後、新しいメンバーシップ関数としてmを得ます。これは、
を見つけた後、新しいメンバーシップ関数としてmを得ます。これは、![]() 入力ベクトルに対応する
入力ベクトルに対応する![]() 、新たなファジー集合を形成することを意味します。
、新たなファジー集合を形成することを意味します。
![]()
このファジー集合の特徴は、そのセットが出力変数のタームセットであるということです。![]()
次に、以下のものが必要です。:
- メンバーシップ関数を
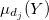 あるレベルで
あるレベルで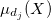 「カット」し、。
「カット」し、。 - ファジーセットを組み合わせます。
言い換えれば、ファジー論理の条件を使用して、条件の意味合いを作ります。- 実行をモデル化する2つの方法があります。プロダクトセットか最小値を見つける。もしくは、合計セットか最大値を見つける。
ファジィ集合を取得した後、その非ファジー性が正確なシステム出力を与えます。
1.4。スゲノ型ファジー推論
スゲノタイプのアルゴリズムによると、ファジー推論はファジー知識ベースによって実行されます。
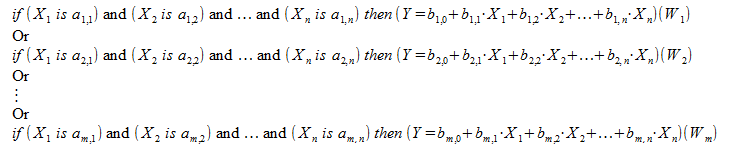
スゲノの知識ベースは、ルール以外マムダニの知識ベースに似ています。![]() ファジー用語によって定義されていない、入力の一次関数:
ファジー用語によって定義されていない、入力の一次関数:
![]()
スゲノ知識ベースのルールは、「入力と出力」を一つの線形則から参照することができます。サブドメインの境界はぼやけていて、したがって、様々な線形性を同時に実行することができます。
この知識ベースは、次のように書くこともできます。
![]()
ここで、以下のことが適用されます
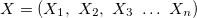 - 入力変数のベクトルは、。
- 入力変数のベクトルは、。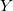 - 出力変数。
- 出力変数。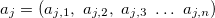 - J =0,1,2...mで入力変数の j番目のルールのベクトル
- J =0,1,2...mで入力変数の j番目のルールのベクトル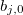 - J =0,1,2...mでの出力値の線形関数での j番目のルールの項の係数
- J =0,1,2...mでの出力値の線形関数での j番目のルールの項の係数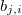 - J =0,1,2...m、i=0,1,2... nである出力値の j番目の一次関数 i番目の係数
- J =0,1,2...m、i=0,1,2... nである出力値の j番目の一次関数 i番目の係数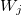 — j番目のルールの重み付け, j = 0,1,2 ... m.
— j番目のルールの重み付け, j = 0,1,2 ... m.
それでは、新しい方法をご紹介しましょう:![]() - ファジィ入力または出力変数 v のメンバーシップ関数t。
- ファジィ入力または出力変数 v のメンバーシップ関数t。
ファジータームの入力ベクトルのメンバーシップ度![]() は、次のように知識ベースから計算されます。:
は、次のように知識ベースから計算されます。:
![]() - この関数は、知識ベースから J番目のルールを特徴付けます。
- この関数は、知識ベースから J番目のルールを特徴付けます。
ただし、![]() - s-ノルム(T-ノルム)演算、すなわちOR(AND)論理演算の実装。スゲノファジィ推論では三角形の実装が、T-ノームとして、最も頻繁に使われます。
- s-ノルム(T-ノルム)演算、すなわちOR(AND)論理演算の実装。スゲノファジィ推論では三角形の実装が、T-ノームとして、最も頻繁に使われます。
![]() for
for![]() を見つけた後、新しいメンバーシップ関数としてmを得ます。これは、
を見つけた後、新しいメンバーシップ関数としてmを得ます。これは、![]() 入力ベクトルに対応する
入力ベクトルに対応する![]() 、新たなファジー集合を形成することを意味します。
、新たなファジー集合を形成することを意味します。
![]()
そのマムダニ出力の結果とは対照的に、前述したファジーセットが最初のオーダーの通常のファジーセットがあるのでご注意ください。これは、正確な数の集合に基づいています。結果の出力値![]() は、n次元の因子空間が与えられた点で行われり線形の依存関係の重ね合わせとして
は、n次元の因子空間が与えられた点で行われり線形の依存関係の重ね合わせとして![]() と定義される。この理由により、ファジィ集合
と定義される。この理由により、ファジィ集合![]() の計算で、加重平均や加重和を計算し、非ファジー化されています。
の計算で、加重平均や加重和を計算し、非ファジー化されています。
2。ファジーロジックライブラリFuzzyNet
実際には、非常に単純なファジーモデルですら、困難な作業です。しかし、大幅に簡素化することができる、さまざまなソフトウェアツールとライブラリがあります。例として、2つのファジーモデルと操作方法についてMQL5 FuzzyNetライブラリのテストスクリプトの内容を確認します。
2.1。マムダニ型システムの設計
最初の例は、スクリプトTips_Sample_Mamdani.mq5FuzzyNetライブラリのサンプルです。これは、サービスに対するチップとして置くチップの計算に使うファジーモデルです。このシステムには、2つのファジーロジックの入力、1つの出力、3つのルールからなる知識ベースとマムダニ型の論理出力のシステムがあります。
ファジー変数は、食品とサービスです。入力パラメータは、両方の変数が0〜10で測定され、これらは、それらの最小値と最大値です。変数"食品"は、2つのタームで構成されています。"ひどい"、"おいしいサービスは3つのタームからなります。ひどい、グッド、エクセレント
出力は、ファジィ変数「チップ」を取得します。5%から30%のヒントの値の範囲を定義します。:安い、平均寛大
システムの知識ベースには、3つのルールが含まれます:
- (食品がひどい)(サービスがひどい)場合、そのチップは安いです。
- (サービスがグッド)場合、チップは平均です。
- (サービスがエクセレント)または(食べ物が美味しい)場合、そのチップは寛大です。
今、システムに関する一般的な考えがあることを、その創造のプロセス内で見なければなりません。
- MQL5ライブラリで、FuzzyNetからMamdaniFuzzySystemをインクルードします。
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>このファイルは、マムダニタイプのシステムを作成し、動作させることができます。 - さて、空のマムダニシステムを作成し、それを埋めます。
MamdaniFuzzySystem *fsTips=new MamdaniFuzzySystem(); - 最初の入力変数「サービス」を作成します。コンストラクタのパラメータとしてファジー変数を作成する場合は、まず、変数の名前がラインで示され、その最小値と最大値が続きます。
FuzzyVariable *fvService=new FuzzyVariable("service",0.0,10.0);
- それにファジータームを追加します。ファジータームコンストラクタは、最初のパラメータと2番目のパラメータ、それらに対応するメンバーシップ関数として、文字列内の名前を使用しています。
fvService.Terms().Add(new FuzzyTerm("poor", new TriangularMembershipFunction(-5.0, 0.0, 5.0))); fvService.Terms().Add(new FuzzyTerm("good", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvService.Terms().Add(new FuzzyTerm("excellent", new TriangularMembershipFunction(5.0, 10.0, 15.0)));
この例では、メンバーシップ関数は、すべてのタームの三角関数として提示されています。 - 今、形成されたファジー変数を、システムに追加します。
fsTips.Input().Add(fvService);
- 同様に、変数「食べ物」の第2の入力を実装しますが、この変数のタームは、台形のメンバーシップ関数を持つことになります。
FuzzyVariable *fvFood=new FuzzyVariable("food",0.0,10.0); fvFood.Terms().Add(new FuzzyTerm("rancid", new TrapezoidMembershipFunction(0.0, 0.0, 1.0, 3.0))); fvFood.Terms().Add(new FuzzyTerm("delicious", new TrapezoidMembershipFunction(7.0, 9.0, 10.0, 10.0))); fsTips.Input().Add(fvFood);
- システムはマムダニ推論を有しているので、その入力値と出力値は、同じ方法により決定ます。そのため、同じような出力を作成します
FuzzyVariable *fvTips=new FuzzyVariable("tips",0.0,30.0); fvTips.Terms().Add(new FuzzyTerm("cheap", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvTips.Terms().Add(new FuzzyTerm("average", new TriangularMembershipFunction(10.0, 15.0, 20.0))); fvTips.Terms().Add(new FuzzyTerm("generous", new TriangularMembershipFunction(20.0, 25.0, 30.0))); fsTips.Output().Add(fvTips);
- システムの知識ベースを示すファジィルールを作成します。ルールを作成するには、文字列表現を与えるためのオプションとしてパースルールメソッドをオブジェクトから呼び出す必要があります。
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is cheap)"); MamdaniFuzzyRule *rule2 = fsTips.ParseRule("if (service is good) then (tips is average)"); MamdaniFuzzyRule *rule3 = fsTips.ParseRule("if (service is excellent) or (food is delicious) then (tips is generous)");
ファジールールの入力は、非キーの単語の使用を許可していませんキーワードは、"if", "then", "is", "and", "or", "not", "(", ")", "slightly", "somewhat", "very", "extremely "です。最後の4つのキーワードは、言語数量詞です。また、利用しているシステムで利用可能なすべての変数名、用語や機能が、キーワードのリストに含まれています。ファジー用語やスゲノ線形関数の重要性は、言語学的な数量詞で増加もしくは減少されています。言語的数量詞には、次の実装が適用されます。
- "少し" - その立方根との条件の結果を置き換えます。大幅に値を低下させます。
- 「やや」 - その平方根の条件の結果を置き換えます。換算値。
- 「非常に」 - セカンドレベルへの条件結果をもたらします。増加値。
- 「非常に」 - 第3レベルの条件結果をもたらします。大幅に値を増加させます。
- "少し" - その立方根との条件の結果を置き換えます。大幅に値を低下させます。
- 残りのステップは、システムにルールを追加することです。
fsTips.Rules().Add(rule1); fsTips.Rules().Add(rule2); fsTips.Rules().Add(rule3);
今、マムダニファジー推論のシステムに基づいて、チップを計算するための既製モデルがあります。
2.2。スゲノ型システムの設計
スゲノタイプのシステムの実装の例として、車の中でのクルーズコントロールシステムの必要な制御を測定するためのスクリプトを使用します。このスクリプトは、MQL5のFuzzyNetライブラリの Cruise_Control_Sample_Sugeno.mq5 ファイルに記述されています。また、自動制御の問題を解決するためのファジィモデルの応用例の一つとして機能します。
ファジー論理は、主に自動制御システム(ACS)における一次元のタスクに使用されます。目標の設定を以下のように説明することができます。:ある時点でのオブジェクト![]() 状態"A"で、時間枠にある
状態"A"で、時間枠にある![]() 状態"B"に到達することがあります。同様のタスクを解決するために、全体的な時間枠を
状態"B"に到達することがあります。同様のタスクを解決するために、全体的な時間枠を![]() 分割し、時間ステップが
分割し、時間ステップが![]() 配置され、すべての点で自動制御システムが管理します。
配置され、すべての点で自動制御システムが管理します。![]() ただし、i=0,1,2... n。
ただし、i=0,1,2... n。
様々なPIDコントローラは、このタスクを簡単に処理するが、「スムーズ」にコントロールすることができないという欠点があります。言い換えれば、速度の変化とPIDコントローラに基づいて、車のクルーズコントロールシステムが構築され、指定の速度に調整されますが、ジャンプして揺れが発生する可能性があります。人の観点からすると、ファジーコントローラがスムーズに実行し、より快適にすることができます。
ファジー制御器の出力に加速に必要な速度変化があり、入力時のエラーと最初のエラー誘導体が発生することは、明白です。エラーは、指定のものからの現在の状態偏差です。言い換えれば、システム入力は次の情報を受信します。
- 現時点およびクルーズコントロールシステムで設定した、車両の速度との差。
- どれくらい早く差が減少するか(増加)。
よって、「スピードエラー」の最初の入力パラメータは、毎時-20から20キロの範囲であり、3つのターム"遅い", "ゼロ", "速い"があります。すべての3つのタームは、三角のメンバーシップ関数を持つことになります。第二の入力 - " SpeedErrorDot"-5から5の範囲であり、ファジーターム遅い"、"ゼロ"、"速く"も三角のメンバーシップ関数を持ちます。
今回のモデルはスゲノの推論システムとして「加速」の出力値を持っているので、最大値と最小値を持っていないでしょう。代わりにファジータームの名前を持っている入力変数の線形結合が存在します。 "ゼロ"、"速く"、"遅い"、"func"。すべての4つの線形の組み合わせを説明してみましょう。![]() 以下の式を得るために、変数 SpeedErrorを
以下の式を得るために、変数 SpeedErrorを![]() 、SpeedErrorDot
、SpeedErrorDot![]() 、つまり加速とします。:
、つまり加速とします。:
- ゼロ:
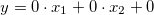 。
。 - 速い:
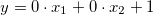 。
。 - 遅い:
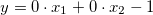 。
。 - func:
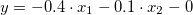 。
。
このシステムの知識ベースは9のルールで構成されます:
- (速度誤差が遅い)、かつ、(速度誤差ドットが遅い)場合、加速度が高速です。
- (速度誤差が遅い)、かつ、(速度誤差の点がゼロである)場合、加速度が速いです。
- (速度誤差が遅い)、かつ、(速度誤差ドットが高速である)場合、加速度はゼロです。
- (速度誤差がゼロである)、かつ、(速度誤差ドットが遅い)場合、加速度が速いです。
- (速度誤差がゼロである)、かつ、(速度誤差の点がゼロである)場合、加速度がfuncです。
- (速度誤差がゼロである)、かつ、(速度誤差ドットが速くなる)場合、加速度が遅いです。
- (速度誤差が高速である)、かつ、(速度誤差ドットが遅い)場合、加速度が高速です。
- (速度誤差が高速である)、かつ、(速度誤差の点がゼロである)場合、加速が遅くなります。
- (速度誤差が高速である)、かつ、(速度誤差ドットが高い)場合、加速が遅くなります。
システム作成の過程を見ていきましょう。:
- MQL5のFuzzyNetライブラリからファイルSugenoFuzzySystem.mqhをインクルードします。
#include <Math\FuzzyNet\SugenoFuzzySystem.mqh>このファイルは、スゲノタイプのシステムを作成し、それを操作することができます。 - 今、空のスゲノシステムを作成し、それを埋めます:
SugenoFuzzySystem *fsCruiseControl=new SugenoFuzzySystem(); - スゲノシステムの入力変数はマムダニタイプのシステムと同じ方法で作成されます。
変数"SpeedError"を作成し、それをシステムに追加します。
FuzzyVariable *fvSpeedError=new FuzzyVariable("SpeedError",-20.0,20.0); fvSpeedError.Terms().Add(new FuzzyTerm("slower",new TriangularMembershipFunction(-35.0,-20.0,-5.0))); fvSpeedError.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-15.0, -0.0, 15.0))); fvSpeedError.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(5.0, 20.0, 35.0)));
"SpeedErrorDot"変数を作成して、それをシステムに追加します。
FuzzyVariable *fvSpeedErrorDot=new FuzzyVariable("SpeedErrorDot",-5.0,5.0); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("slower", new TriangularMembershipFunction(-9.0, -5.0, -1.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-4.0, -0.0, 4.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(1.0, 5.0, 9.0)));
- システムの出力となるスゲノ型ファジー変数を作成します。ファジー変数を作成する場合、コンストラクタは、唯一のパラメータとしてその名を受けます。線形関数は、追加することができますが、最初にこれらの機能を決定する必要があり、このため、doubleの係数の配列が必要となります。
線形関数の形成は、以下のようになります。:各入力変数は係数の配列から得られた係数を持つ未知の方程式となります。配列の係数は、入力変数と同じ順序で配置されなければなりません。このように、最初の入力変数のインデックス0の係数は、インデックス1など,適用されますしたがって、係数の配列の長さは、入力変数よりも大きくなければなりません。配列の長さが等しい場合、項の係数がゼロに等しくなります。そうでなければ、その値は配列の最後の要素に等しくなります。
システム内の2つの入力変数であるため、係数の配列の長さが3を超えないようにしてください。上述した形に基づいて、すべての4つの配列を宣言し、スゲノ型ファジー変数に追加します:SugenoVariable *svAccelerate=new SugenoVariable("Accelerate"); double coeff1[3]={0.0,0.0,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("zero",coeff1)); double coeff2[3]={0.0,0.0,1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("faster",coeff2)); double coeff3[3]={0.0,0.0,-1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("slower",coeff3)); double coeff4[3]={-0.04,-0.1,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("func",coeff4)); fsCruiseControl.Output().Add(svAccelerate);
- それぞれマムダニシステムで、ファジールールを作成します。
SugenoFuzzyRule *rule1 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule2 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is zero) then (Accelerate is faster)"); SugenoFuzzyRule *rule3 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is faster) then (Accelerate is zero)"); SugenoFuzzyRule *rule4 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule5 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is zero) then (Accelerate is func)"); SugenoFuzzyRule *rule6 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is faster) then (Accelerate is slower)"); SugenoFuzzyRule *rule7 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule8 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is zero) then (Accelerate is slower)"); SugenoFuzzyRule *rule9 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is faster) then (Accelerate is slower)");
- システムを追加します:
fsCruiseControl.Rules().Add(rule1); fsCruiseControl.Rules().Add(rule2); fsCruiseControl.Rules().Add(rule3); fsCruiseControl.Rules().Add(rule4); fsCruiseControl.Rules().Add(rule5); fsCruiseControl.Rules().Add(rule6); fsCruiseControl.Rules().Add(rule7); fsCruiseControl.Rules().Add(rule8); fsCruiseControl.Rules().Add(rule9);
2.3。マムダニ型とスゲノ型システムの計算
ファジー変数とその値は、ファジーシステムの入力に送られます。前述のように、ファジー変数は、それらのタームセットから値を取ります。そのため、システムの計算結果は、ファジー入力変数とタームに対応したメンバーシップ関数に依存します。しかし、ほとんどの場合、出力で正確な結果を得ることを目的として、ファジー変数が単純な数値の形で、入力システムに送信されます。この場合、ファジータームは明らかに宣言がなく、そのメンバーシップ関数は、一定のメンバーシップ関数として表されることが分かります。FuzzyNetライブラリによるシステムは、このような特定のケースで動作するように設計されています。
何を正確にシステムの入力に送る必要があり、どのような形でその結果を取得しましょう?
ファジーシステムの入力変数の数は限定されるものではなく、各エントリは値を取る必要があります。したがって、各入力の値を格納するリストが必要です。2つのフィールドを持つ複雑なオブジェクトがこのリストの要素でなければなりません: - ファジー変数、2番目のフィールド - 最初のフィールドの数値型double。Dictionary.mqhでは、ライブラリFuzzyNet MQL5より、クラスDictionary_Obj_Doubleが、オブジェクトを作成できるように実装されました。
マムダニ型システムの入力リストを形成します。
CList *in=new CList; Dictionary_Obj_Double *p_od_Service=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_Food=new Dictionary_Obj_Double; p_od_Service.SetAll(fvService, Service); p_od_Food.SetAll(fvFood, Food); in.Add(p_od_Service); in.Add(p_od_Food);
ここで、サービスと食品 - double型の2つの入力パラメータです。
一般的には、入力と同様に量には制限はありませんが、上記の例では、マムダニとスゲノ両方のシステムでは、1つの出力だけあります。入力と出力の構造に違いはありません。
マムダニ型システムの出力:
CList *result=new CList; Dictionary_Obj_Double *p_od_Tips=new Dictionary_Obj_Double;
さて、各システムで、1つのパラメーターを有するCalculate関数を呼び出します。このパラメーターは、入力のリスト、および出力のリストを返します。リストからインデックス0によると、Dictionary_Obj_Doubleクラスのオブジェクトとして表現されているシステムの出力値を取得します。このオブジェクトのメソッドに使用したKeyと値は、それぞれ、その結果を変数を取得することができます。
マムダニシステムの計算を行い、ファジー出力変数fvTipsで受信した番号が表示されます。
result=fsTips.Calculate(in); p_od_Tips=result.GetNodeAtIndex(0); Alert("Tips, %: ",p_od_Tips.Value());
スゲノタイプのシステムと同じことをしなければなりません。
CList *in=new CList; Dictionary_Obj_Double *p_od_Error=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_ErrorDot=new Dictionary_Obj_Double; p_od_Error.SetAll(fvSpeedError,Speed_Error); p_od_ErrorDot.SetAll(fvSpeedErrorDot,Speed_ErrorDot); in.Add(p_od_Error); in.Add(p_od_ErrorDot); CList *result=new CList; Dictionary_Obj_Double *p_od_Accelerate=new Dictionary_Obj_Double; result=fsCruiseControl.Calculate(in); p_od_Accelerate=result.GetNodeAtIndex(0); Alert("Accelerate, %: ",p_od_Accelerate.Value()*100);
結論
同様なファジーモデルを作成するには、 MQL5または MQL4のFuzzyNetライブラリをダウンロードしてください。"ライブ"でのファジーモデルの構築は、やりがいはありますが、補助ライブラリの支援が必要です。また、完成モデルでは、徹底したチェックや調整を必要とします。
参考文献とリンクの一覧
- http://www.bindichen.co.uk/post/AI/mamdani-fuzzy-model.html - マムダニファジーモデル。
- http://www.bindichen.co.uk/post/AI/takagi-sugeno-fuzzy-model.html - スゲノファジーモデル。
- http://reference.wolfram.com/applications/fuzzylogic/DemonstrationNotebooks/5.html - ファジー論理制御。
- http://plato.stanford.edu/entries/logic-fuzzy</a0 - ファジー論理の紹介。
- Lotfi A. Zadeh. ファジー集合とその応用
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/1991
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
 テクニカル分析におけるトーマス・デマーク
テクニカル分析におけるトーマス・デマーク
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
ハイ
メタトレーダーをビルド2342にアップデートしたところ
ファジィロジックライブラリを使用したすべてのサンプル
return error "incorrect casting of pointers" on MQL5Include\Math Fuzzy\RuleParser.mqh Line 712
バグを修正するのを手伝ってください
多謝
前の投稿を読む
ハイ
リプレイありがとう
本当の作者はDmitry Kalyuzhnyですが、彼はこのライブラリを.Netでコーディングしました。
しかし、多分他の誰かがコードをmqlに変更したのでしょう。
この記事の著者はДмитрий Калюжныйですね。
しかし、私はmql5のДмитрий Калюжныйプロファイルを 見つけることができませんでした。
このバグに連絡するか、修正する方法を教えてください。
ありがとうございました。
ファジィ論理入門」が掲載されました:
著者MetaQuotes Software Corp.
こんにちは
メタトレーダーをビルド2342にアップデートしたところ
ファジィロジックライブラリを使用したすべてのサンプルで
return error "incorrect casting of pointers" on MQL5Include\Math Fuzzy\RuleParser.mqh Line 712
バグを修正するのを助けてください
どうもありがとう
ハイ
リプレイありがとう
本当の作者はDmitry Kalyuzhnyですが、彼はこのライブラリを.Netでコーディングしました。
しかし、多分他の誰かがコードをmqlに変更したのでしょう。
この記事の著者はДмитрий Калюжныйであることがわかった。
しかし、mql5でДмитрий Калюжныйのプロフィールを 見つけられなかった。
このバグに連絡するか、修正するのを手伝ってくれませんか?
ありがとうございました。
このスレッドで誰も助けない場合は、例えば、フリーランスを 使用することができます。
こんにちは、
言語的量詞 "について質問があります: " slightly"、"somewhat"、"very"、"extremely "...
ParseRule-functionでのこれらの正しい使い方を教えてください。
このような使い方をすると、次のようなエラーが出ます:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is very cheap)");...こんなエラーが出る:"ルールの結論部分は次の形式であるべきです:変数は項である"
上の文字列のどこに「very」を入れればいいのでしょうか?
助けていただけると助かります!
ありがとうございました!