Características del Wizard MQL5 que debe conocer (Parte 30): Normalización por lotes en el aprendizaje automático

Introducción

La normalización por lotes, una forma de estandarizar los datos antes de introducirlos en las capas de las redes neuronales, está mejorando el rendimiento de las redes y, sin embargo, hay cierto desacuerdo en cuanto a las causas. Mientras que en el documento original sobre el tema, la razón expuesta era un desplazamiento interno de covariables que puede entenderse como la mitigación de los efectos de los desequilibrios en los datos de entrada de los "estratos superiores" para que no tengan efectos en cascada en los estratos inferiores, este estudio más reciente afirma que las mejoras en el rendimiento empírico se deben al suavizado, ya que los gradientes intracapa tienen menos variabilidad dada la normalización.

Desde el punto de vista de un operador, el interés por saber POR QUÉ la normalización por lotes influye en el rendimiento de una red neuronal es motivo más que suficiente para desarrollar y probar sistemas que la utilicen, y ésa es nuestra tarea. Existen tres formas principales de normalización de lotes que examinaremos, a saber Escalado estándar, Escalado de características y Escalado robusto. Cada uno de estos es un algoritmo muy simple, haremos pruebas con Asesores Expertos utilizando cada uno, y como control también haremos pruebas con Asesores Expertos que no utilizan la normalización por lotes. Así pues, nuestro artículo volverá al formato que habíamos estado utilizando antes de los dos últimos artículos (sobre los índices de aprendizaje), en los que ahora tendremos descripciones de las tres normalizaciones, luego informes de pruebas de las mismas con un control y, por último, una conclusión.

Este artículo, como todos los de esta serie, destaca el uso de Asesores Expertos montados por asistentes para probar nuevas ideas. Las introducciones sobre cómo se hace esto se pueden obtener de aquí y aquí para los nuevos lectores, con esos 2 artículos que proporcionan alguna orientación sobre cómo utilizar el código adjunto al final de este artículo. Para esta pieza, estamos utilizando bastantes enumeraciones personalizadas de datos como entradas optimizables. Las enumeraciones incorporadas en MQL5 se pueden declarar en la cabecera del archivo de señal personalizado, y se indicarán automáticamente como entradas y se inicializarán como parte del filtro de señal. Sin embargo, cuando las enumeraciones son personalizadas, colocarlas en la cabecera impedirá que el archivo sea visible (o reconocible) en el Asistente MQL5, lo que significa que no podrás realizar el ensamblaje del asistente. La solución que tenemos, por ahora, es omitirlos de la cabecera de la clase de señal personalizada, pero tener los parámetros y sus funciones de asignación declarados dentro de la clase de señal, como es siempre el caso con cualquier parámetro de entrada. Una vez finalizado el montaje del asistente, realizamos cambios manuales en la lista de parámetros de entrada y también en la inicialización de la clase signal para añadir estos parámetros de enumeración personalizados.

Había un truco que había encontrado sobre esto que creo que implicaba declarar las enumeraciones en la propia clase de señal, pero no recuerdo los detalles, así que tendremos que conformarnos con esta edición manual. Nuestro Asesor Experto de prueba tiene enumeraciones personalizadas para el tipo de tasa de aprendizaje, el tipo de tasa de aprendizaje adaptativo y, lo que es más importante para este artículo, una enumeración sobre los tipos de normalización. El código de este último se comparte a continuación:

enum Enormalize
{  NORMALIZE_NONE = -1,
   NORMALIZE_ROBUST = 0,
   NORMALIZE_FEATURE = 1,
   NORMALIZE_STANDARD = 2,
};

Para utilizar y optimizar esta enumeración dentro del Asesor Experto, tendríamos que añadir manualmente los parámetros de la enumeración como entradas, de la siguiente manera:

....

input ENUM_ACTIVATION_FUNCTION Signal_CMLP_ActivationType = AF_SIGMOID;  // CMLP(30,6,0.05,10,0.1,2,...) Activation Type
input Enormalize Signal_CMLP_NormalizeType   = NORMALIZE_FEATURE; // CMLP(30,6,0.05,10,0.1,2,...) Batch Normalisation Type
input Elearning Signal_CMLP_LearningType   = LEARNING_ADAPTIVE; // CMLP(30,6,0.05,10,0.1,2,...) Learning Type
input Eadaptive Signal_CMLP_AdaptiveType   = ADAPTIVE_GRADIENT; // CMLP(30,6,0.05,10,0.1,2,...) Adaptive Type

...

In addition, we would need to add the declared parameters to the instance of the custom signal, which is initialized as ‘filter0’. Esto se hace de la siguiente manera:

...

   filter0.ActivationType(Signal_CMLP_ActivationType);
   filter0.NormalizeType(Signal_CMLP_NormalizeType);
   filter0.LearningType(Signal_CMLP_LearningType);
   filter0.AdaptiveType(Signal_CMLP_AdaptiveType);

...

Una vez hecho esto, el asistente del experto montado se puede utilizar normalmente con nuestra clase de señal personalizada. Después de haber presentado los 3 formatos de normalización que vamos a considerar a través de la enumeración personalizada anterior, ahora tengamos una breve descripción general del tema, antes de analizar con más profundidad cada uno de los tipos de enumeración por lotes, después de lo cual consideraremos la implementación general en la clase de señal personalizada.

Argumentos a favor de la normalización por lotes en redes neuronales

Oficialmente, la mayoría de los beneficios de la normalización de lotes siguen evolucionando en torno a los argumentos esgrimidos en el artículo que lo sacó a la luz en 2015. Dado que actualmente existe un debate sobre cómo es capaz de lograr sus resultados empíricos, estos argumentos originales pueden no tener necesariamente el mismo peso que tenían al principio. De todos modos, los presentamos aquí, al menos, como una introducción al tema. Se promociona la normalización por lotes para estabilizar el proceso de entrenamiento al reducir el cambio de covariable interna mencionado anteriormente. Mejora la velocidad de convergencia ya que las activaciones en cada capa son 'más estándar'. Además, reduce la sensibilidad a los pesos de inicialización utilizados en una red antes del entrenamiento. Los pesos iniciales tienden a tener una influencia desproporcionada no sólo en los pesos finales a los que se llega, sino también en la duración del proceso de entrenamiento.

Además, la normalización por lotes actúa como un regularizador al hacer que la red sea menos sensible a los pesos de algunas neuronas. También permite el entrenamiento de redes neuronales profundas al reducir los problemas de gradiente evanescente. Desacopla las dependencias de capas, hace que el proceso de entrenamiento sea invariable a los cambios en la escala de las características de entrada, mejora la generalización del modelo, facilita el entrenamiento de lotes de diferentes tamaños y está bien preparado para experimentar con varios programas de tasas de aprendizaje. Estas son algunas de las ventajas promocionadas de la normalización de lotes. Consideremos ahora cada tipo.

Escalado de características

Esta forma de normalización convierte todos los datos de un vector en una capa en el rango de 0,0 a +1,0. La fórmula para esto para cada valor del vector es:

Donde:

• x' es el valor normalizado
• x es el valor original desnormalizado
• min(x) es una función que devuelve el mínimo del vector
• max(x) devuelve el máximo del vector

La implementación de este algoritmo tan simple sería sencilla en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Function to apply Feature-Scaling
//+------------------------------------------------------------------+
void Cnormalize::FeatureScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min());
      }
   }
}

Al seleccionar un algoritmo de normalización, el tipo de activación que se utilizará en cada capa es una consideración importante. Esto se debe a que no todas las funciones de activación generan sus resultados en el mismo rango. A continuación se muestra una tabulación de las diversas funciones de activación, disponible como enumeración en MQL5, y sus respectivos rangos de salida:

Función de activación	Rango de salida
Unidad lineal exponencial (Exponential Linear Unit, ELU)		(-1, ∞)
Exponencial (Exp)		(0, ∞)
Unidad lineal de error gaussiano (Gaussian Error Linear Unit, GELU)		(-∞, ∞)
Sigmoide duro		[0, 1]
Lineal		(-∞, ∞)
Unidad lineal rectificada con fugas (Leaky Rectified Linear Unit, Leaky ReLU)		(-∞, ∞)
Unidad lineal rectificada (Rectified Linear Unit, ReLU)		[0, ∞)
Unidad lineal exponencial escalada (Scaled Exponential Linear Unit, SELU)		(-∞, ∞)
Sigmoideo		(0, 1)
Máximo suave		(0, 1), suma 1
Más suave		(0, ∞)
Señal suave		(-1, 1)
Swish		(-∞, ∞)
Tangente hiperbólica (Hyperbolic Tangent, Tanh)		(-1, 1)
Unidad lineal rectificada con umbral (Thresholded Rectified Linear Unit, Thresholded ReLU)		{0} ∪ [θ, ∞), donde θ > 0

Como es evidente, sólo tenemos 3 funciones de activación que proporcionan salidas dentro de un rango similar al algoritmo de normalización por lotes de escalado de características. Estos son sigmoide duro, sigmoide y máximo suave. Todo lo demás está fuera de los límites. Esta coincidencia de rangos de salida es vital para que las redes eviten los problemas de gradiente desaparecido/explotado que ocurren con frecuencia durante el entrenamiento.

La activación sigmoidea dura es una aproximación simple de la función sigmoidea que se define mediante la siguiente ecuación:

Por lo tanto, independientemente de qué entrada tengamos para 'x', la salida estará limitada en un rango de 0,0 a +1,0. Esta adaptación al escalamiento de funciones garantiza activaciones consistentes e interpretables. Además, la sigmoide dura es computacionalmente eficiente y, por lo tanto, adecuada para redes grandes y muy profundas como los transformadores.

La función de activación sigmoidea es posiblemente la más popular de todas las activaciones debido a la forma en que minimiza los problemas de gradientes explosivos a través de la salida controlada por rango que aún logra mantener cierto grado de variabilidad, a diferencia de, por ejemplo, la activación sigmoidea dura mencionada anteriormente. Su ecuación es la siguiente:

Donde:

• 'e' es la constante de Euler
• 'x' is the normalized value

La suavidad de su mapeo se alinea bien con el rango de escala de características normalizadas. Además, evita problemas con la saturación del gradiente, ya que los valores de salida de 0,0 o 1,0 son raros.

La activación máxima suave normaliza una clase (o digamos un vector de datos) de modo que todos sus valores no solo estén en el rango de 0,0 a 1,0, sino que además estos valores normalizados, cuando se suman, suman 1,0. La ecuación que deriva esto se indica a continuación:

Donde:

• 'z i' es el i-ésimo elemento del vector de entrada 'Z'.
• K es el tamaño del vector de Z
• 'e' es la constante de Euler

El máximo suave se utiliza normalmente en la clasificación de múltiples clases o en la comparación de puntos de datos que tienen más de una dimensión. El resultado implica una distribución de probabilidad en la que ningún resultado domina desproporcionadamente a los demás, lo que crea una especie de campo de juego parejo. Además, la suma de uno garantiza que no haya números grandes que puedan crear problemas de cálculo posteriores en redes o transformadores muy profundos.

Por lo tanto, sigmoide duro, sigmoide y máximo suave son los tres algoritmos de función de activación adecuados para la normalización de escalamiento de características, ya que las salidas de los tres tienden a coincidir con las salidas de esta normalización por lotes. La implementación de estos algoritmos en MQL5 es realmente sencilla, ya que se puede acceder a todos los algoritmos de activación y sus respectivos derivados desde las funciones integradas del tipo de datos vectorial. Ejemplos de esto están en las funciones 'Forward()' y 'Backward()' que forman parte de la clase 'Cmlp' que se adjunta a este artículo. Alternativamente, la orientación oficial también está disponible tanto para las funciones de activación como para las funciones derivadas.

La implementación del algoritmo de escalamiento de características ya se ha destacado anteriormente. Es una función sencilla que verifica las divisiones por cero al garantizar que los valores máximo y mínimo del vector no sean los mismos. Las funciones de escalamiento son muy simples y esto es importante para minimizar el cómputo dado que muchas redes pueden ser muy profundas y estar en formato de transformador.

Escalabilidad robusta

Esta forma de normalización proporciona un poco más de margen en su salida al proporcionar valores que se extienden ligeramente más allá de -1,0 y +1,0 en ciertas condiciones, pero en la mayoría de los casos todos los datos suelen estar entre -1,0 y +1,0. Las excepciones a esto son comunes y ocurren en casos en que hay valores atípicos cuya distancia de la mediana es tan grande que excede el rango intercuartil. La ecuación que rige esto es la siguiente:

Donde:

• 'x' es el valor original
• mediana(x) es la mediana del vector o clase
• IQR(x) es el percentil 75^º menos el percentil 25^º de la clase.

Si bien el escalamiento robusto es menos sensible a los valores atípicos que el escalamiento de características, no los ignora. De hecho, los valores atípicos que se alejan de la mediana son los que tienden a proporcionar valores normalizados cuya magnitud es superior a uno. Además, en general, si hay una alta variabilidad en los datos (el rango máximo a mínimo) en comparación con el rango intercuartil; en otras palabras, una situación en la que los datos están centrados predominantemente alrededor de la mediana pero con un número que disminuye gradualmente hacia los extremos, de modo que los valores extremos no son necesariamente valores atípicos. En estos casos, también, los valores más cercanos al extremo tendrán normalizaciones con magnitudes superiores a uno.

De nuestra tabla anterior sobre rangos de salida de activación, queda claro que la elección ideal de funciones de activación para combinar con un escalamiento robusto sería la activación de signo suave o la activación TANH. Esto se debe a que sus salidas, aunque un poco restrictivas al rango de -1.0 a +1.0 dados los posibles efectos atípicos de escalamiento robusto que hemos mencionado anteriormente, son la que mejor se adapta a todas las demás activaciones. Pero lo más importante es que estas salidas de activación no producen valores infinitos, por lo que el riesgo de desaparición y explosión de gradientes se mitiga enormemente.

El signo suave se define mediante una ecuación muy simple:

Donde:

• 'x' es el punto de datos en la clase o vector
• |x| es la magnitud de estos datos

Según su fórmula, su 'x' clara, o los datos dentro de un vector normalizado, deberían ser idealmente de tipo punto flotante y probablemente tener una magnitud que oscile entre 0,0 y 2,0. A medida que los valores 'x' aumentan a partir de 2,0, la variabilidad y, por lo tanto, la interpretación de los datos normalizados se verían obstaculizadas. Esto indica la saturación de los valores normalizados alejándose de cero, pero una transición suave alrededor del valor cero. La simetría y el centrado de los valores alrededor del cero se alinean bien con el escalamiento robusto. Además, se ha observado que los gradientes de signo suave no desaparecen tan fácilmente como los de otras funciones de activación, como la popular activación sigmoidea. Esto puede ser muy beneficioso cuando se realiza un entrenamiento extenso en grandes conjuntos de datos.

La activación de TANH es otro algoritmo con límite de rango de -1,0 a +1,0 que debería funcionar bien y con un escalamiento robusto. Su ecuación se da a continuación:

Donde:

• 'x' es un punto de datos dentro de la clase o vector
• 'e' es la constante de Euler

El algoritmo TANH en forma es muy similar al sigmoide, con la distinción obvia de que está centrado alrededor de 0,0 mientras que el sigmoide está centrado alrededor de 0,5. También se informa que proporciona un gradiente más suave que la función sigmoidea. El rango de signos, al igual que el de los signos suaves, lo convierte en otro candidato ideal para trabajar con escalamiento robusto, como hemos visto anteriormente. Los datos ruidosos o conjuntos de datos con muchos valores atípicos, que desde la perspectiva de un comerciante podrían incluir amortiguadores de precios de valores muy volátiles, son todos conjuntos de datos ideales para usar con escalamiento robusto y activación de TANH. Esto se debe a su capacidad para manejar conjuntos de datos con escalas variadas.

La implementación en MQL5 es tan sencilla como decimos con las tres funciones de activación para escalado de características mencionadas anteriormente. El tipo de datos vectoriales tiene funciones de activación y derivadas integradas que generan resultados en cualquier vector que también sirva como entrada. Esto se describe a continuación aquí y aquí respectivamente como ya se compartió anteriormente.

El algoritmo de escalamiento robusto se implementa en una clase normalizada en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Function to apply Robust-Scaling
//+------------------------------------------------------------------+
void Cnormalize::RobustScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Percentile(75) - _copy.Percentile(25) > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Median()) / (_copy.Percentile(75) - _copy.Percentile(25));
      }
   }
}

Al igual que el algoritmo de escalamiento de características anterior, se realiza una verificación de divisiones de cero en el rango intercuartil. Nuevamente se trata de un algoritmo simple por las razones de eficiencia ya destacadas anteriormente.

Puntuación estándar

La puntuación estándar, que probablemente sea más común, ya que el puntaje Z (Z-Score) es posiblemente el algoritmo de normalización más popular. En la página de Wikipedia sobre la normalización por lotes, es la única función de normalización utilizada. Se trata de transformar una clase o vector de datos en valores cuya media sea 0 y cuya desviación estándar sea 1. Esto es claramente diferente de los casos de escalamiento de características y escalamiento robusto que hemos considerado anteriormente, donde el foco estaba en el rango de los datos de salida. Su ecuación es la siguiente:

Donde:

• Z es el valor normalizado
• μ es la media
• σ es la desviación estándar

De esta ecuación podemos ver que la salida tiene un rango ilimitado, de modo que las salidas posibles pueden abarcar desde menos infinito hasta más infinito. Esto debería ser una señal de alerta, ya que los gradientes explosivos pueden convertirse rápidamente en un problema, especialmente si las funciones de activación que se utilizan con esto también tienen salidas no ligadas. Sin embargo, centra sus salidas alrededor de cero, y esto es bueno para estabilizar el proceso de entrenamiento de redes que utilizan descenso de gradiente. Además, es muy eficaz cuando se trabaja con datos distribuidos normalmente, ya que garantiza que los puntos de datos de entrada contribuyan de manera uniforme al proceso de aprendizaje.

También tiene desventajas, aunque la principal es la sensibilidad a los valores atípicos, la presunción de una distribución gaussiana de los datos y, como ya se dijo, una salida sin límites. La implementación de esta puntuación estándar en MQL5 se puede lograr de la siguiente manera:

//+------------------------------------------------------------------+
//| Function to apply Standard-Score
//+------------------------------------------------------------------+
void Cnormalize::StandardScore(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Std() != 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Mean()) / _copy.Std();
      }
   }
}

Curiosamente, esta todavía no es una característica estándar entre las funciones MQL5. Para evitar divisiones de cero para todas estas tres funciones de normalización, en lugar de verificar un denominador cero, también es común agregar un pequeño valor doble distinto de cero en la parte inferior, a menudo denominado épsilon. Sin embargo, esta práctica, cuando se realiza con escalamiento de características o escalamiento robusto, puede generar valores normalizados muy grandes en el caso de que el denominador potencial fuera cero.

Transformador de normalización

Una vez que los datos de entrada de la capa se han normalizado mediante escalamiento de características, escalamiento robusto o puntuación estándar, los resultados de estas normalizaciones se introducen en el transformador de normalización por lotes. También es una función relativamente sencilla que se define mediante la siguiente ecuación:

Donde:

• 'y' representa la salida en el vector en el índice 'i'
• 'x' es el punto de datos normalizado previamente en el índice 'i'
• Gamma y Beta son parámetros de punto flotante optimizables

Codificar esto tampoco requiere mucho tiempo, ya que podemos tenerlo en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Batch Normalizing Transform
//+------------------------------------------------------------------+
void Cnormalize::Transform(Enormalize Type, vector &Output, vector &BatchTransform, vector &Beta, vector &Gamma)
{  if(Type != NORMALIZE_NONE)
   {  if(Type == NORMALIZE_STANDARD)
      {  StandardScore(Output);
      }
      else if(Type == NORMALIZE_FEATURE)
      {  FeatureScaling(Output);
      }
      else if(Type == NORMALIZE_ROBUST)
      {  RobustScaling(Output);
      }
      //Transformer
      BatchTransform.Init(Output.Size());
      BatchTransform.Fill(0.0);
      for(int i = 0; i < int(Output.Size()); i++)
      {  BatchTransform[i] = (Gamma[i] * Output[i]) + Beta[i];
      }
   }
}

Los argumentos para tomar la salida de normalización a través de este transformador son principalmente cinco. En primer lugar, restaura el poder representativo de los datos originales no normalizados introduciendo flexibilidad y recalibración. Flexibilidad porque después de la transformación los datos de salida pueden no estar necesariamente en un estado óptimo para facilitar el aprendizaje de la red. Por ejemplo, al utilizar la normalización de puntuación estándar, los datos de salida de cada vector siempre tienen una media de 0 y una desviación estándar de 1. Este y otros casos similares pueden ser demasiado extremos para que la red pueda entrenarse eficazmente. Es por eso que la introducción de parámetros beta y gamma que se puedan aprender y optimizar puede ayudar a recalibrar estos conjuntos de datos a una forma óptima para el entrenamiento.

En segundo lugar, en los casos en que la función de normalización inicial tiene salidas potencialmente no acotadas, como, nuevamente, la puntuación estándar, este transformador de normalización puede ayudar a evitar gradientes que desaparecen o explotan. Esto se lograría ajustando beta y gamma. En tercer lugar, se argumenta que el transformador mantiene la varianza para un aprendizaje efectivo a través del escalamiento de la varianza. El parámetro gamma puede ajustar la varianza de las salidas normalizadas ya que es un múltiplo directo. Con esta capacidad de ajustar esta varianza, el proceso de aprendizaje se puede ajustar para adaptarse a la arquitectura de la red.

Además, el transformador puede mejorar la dinámica de aprendizaje de una red al hacer que la red se adapte a los datos, lo que a menudo conduce a mejoras en la convergencia. Los parámetros beta y gamma optimizables guían una vez más este proceso de modo que los datos se escalen para utilizar mejor las configuraciones de tamaño y número de capas de red, siendo el resultado final de esto menos épocas de entrenamiento necesarias para lograr resultados ideales. Finalmente, se argumenta que una regularización a partir del escalamiento y desplazamiento de las salidas de los datos normalizados funciona como una regularización por abandono. La regularización tiene como objetivo impulsar a la red a aprender más sobre los patrones subyacentes en un conjunto de datos y menos sobre el ruido, de modo que los parámetros beta y gamma, que son parámetros vectoriales, sean únicos para cada capa. Esta personalización en base a parámetros, además de regularizar la red, también permite realizar mejor el desplazamiento de covariables del que hablamos en la introducción gracias a la acción específica de los parámetros beta y gamma.

Resultados de la prueba de estrategia

Para las pruebas, utilizamos el símbolo EURJPY en el marco temporal diario para el año 2023. La normalización de la puntuación estándar, al tratarse de datos no ligados, no necesariamente tiene una función de activación del pretendiente. Se pueden utilizar las funciones de activación limitadas que hemos mencionado en este artículo, sin embargo, esa prueba queda en manos del lector. Para nuestros propósitos, estamos probando únicamente la normalización de escala robusta y la normalización de escala de características. Los combinamos con la activación de signo suave y sigmoidea, respectivamente.

Para el escalamiento de características, obtuvimos los siguientes resultados:

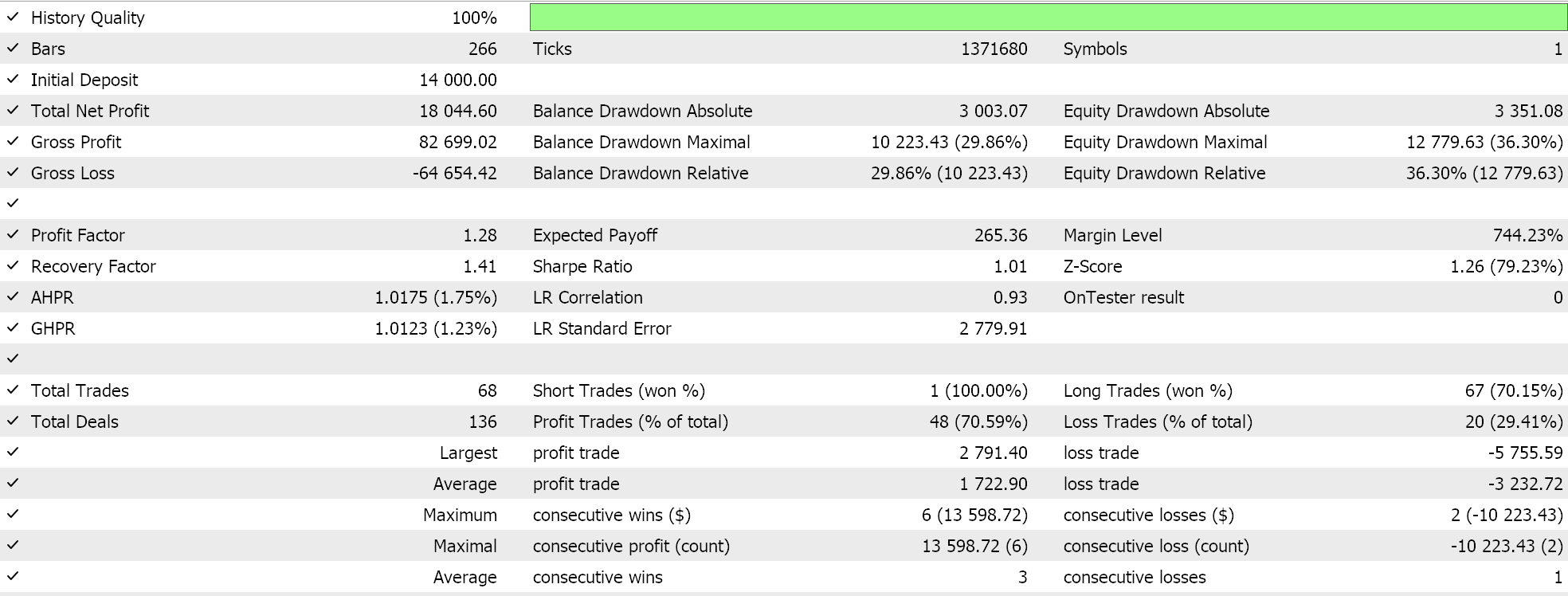
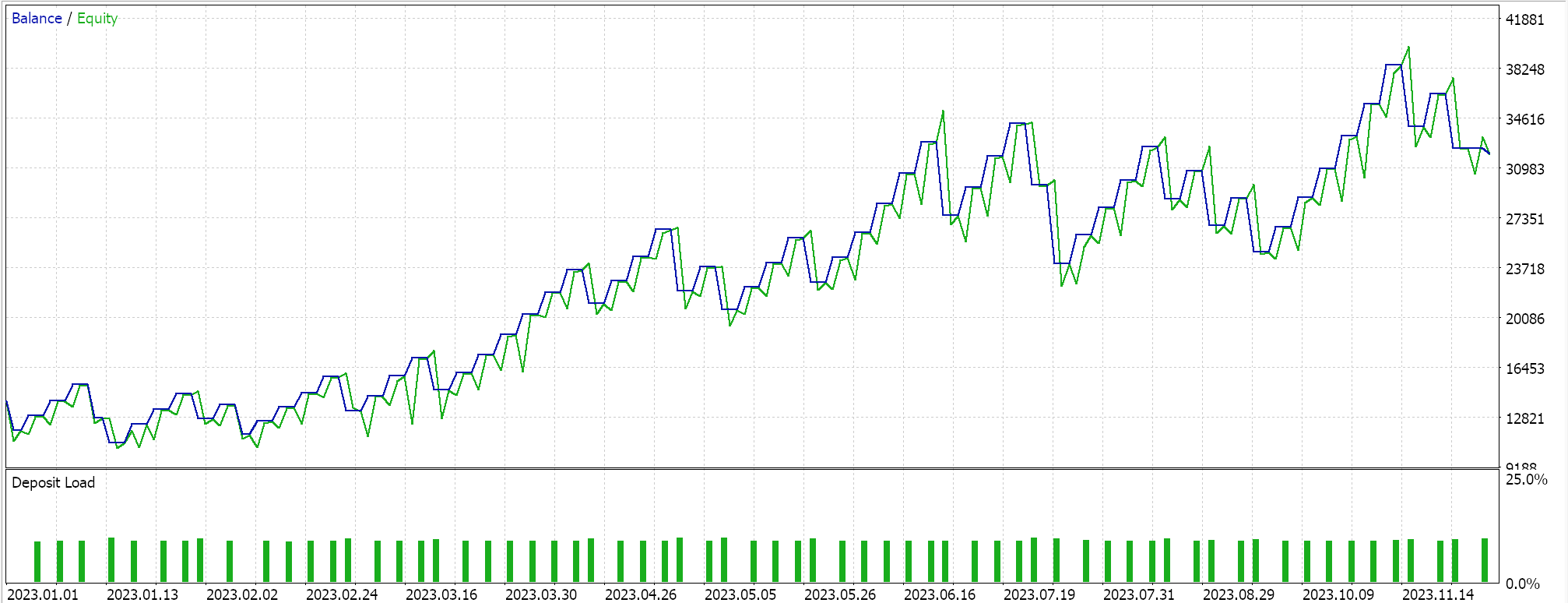
Para un escalamiento robusto, teníamos:

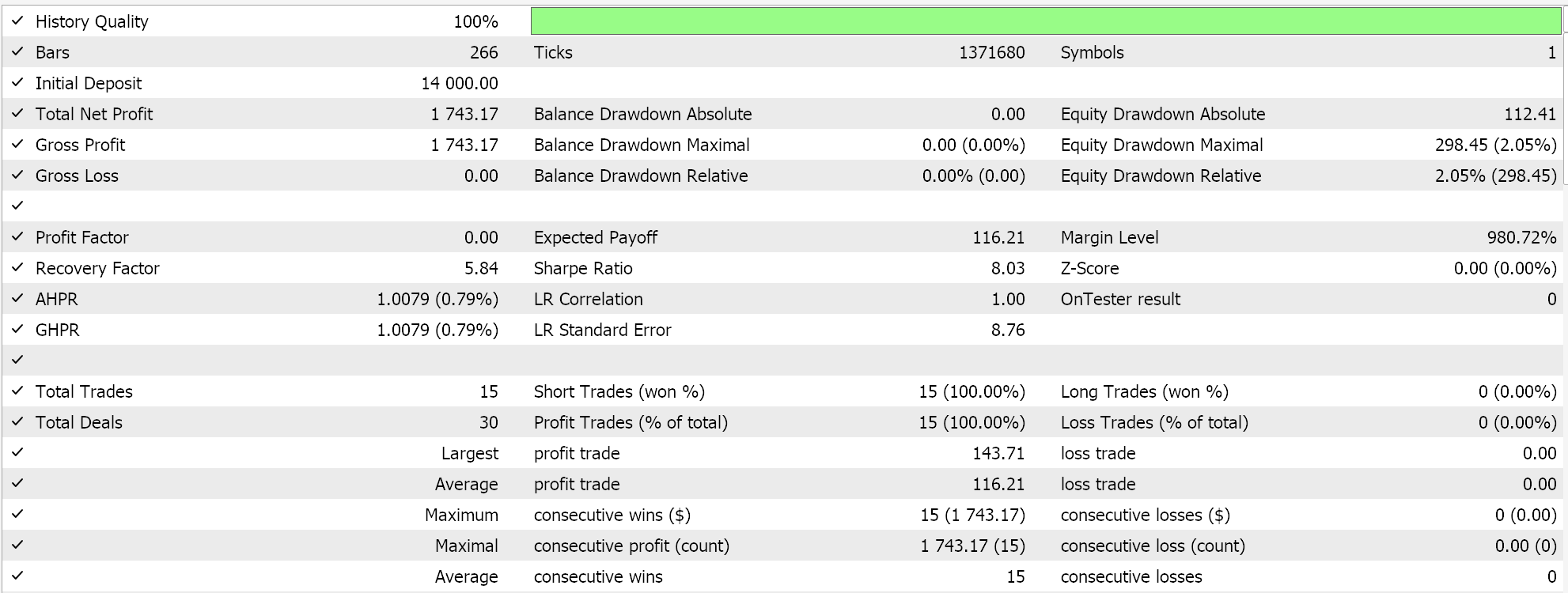
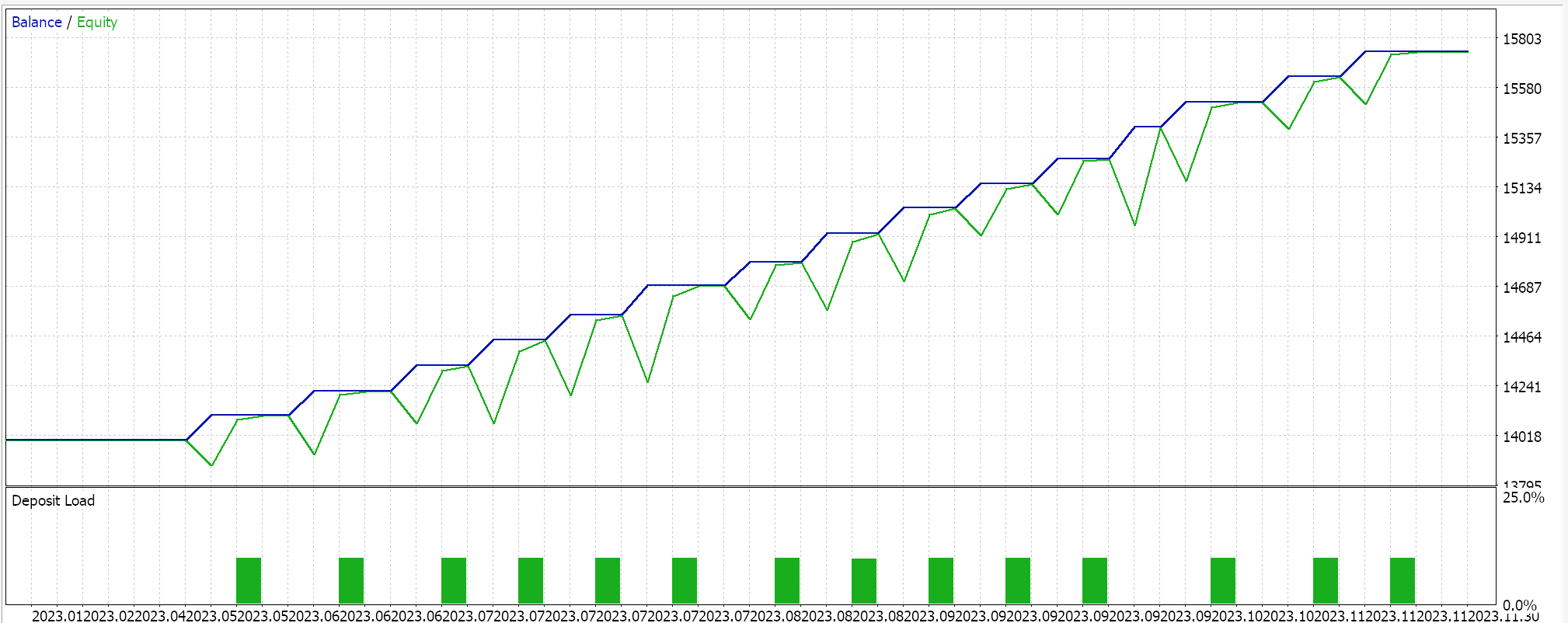
Como control, realizamos pruebas con el Asesor Experto ejecutando configuraciones idénticas pero sin normalización. A continuación se muestran nuestros resultados:

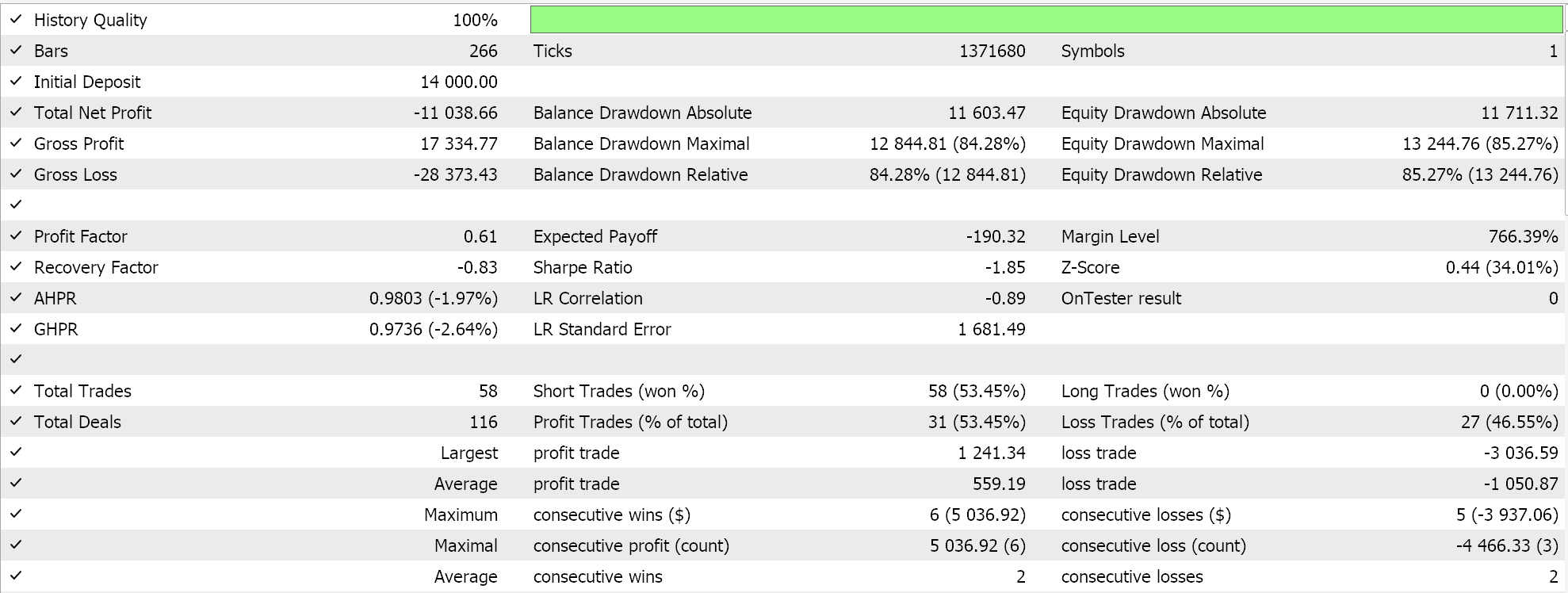
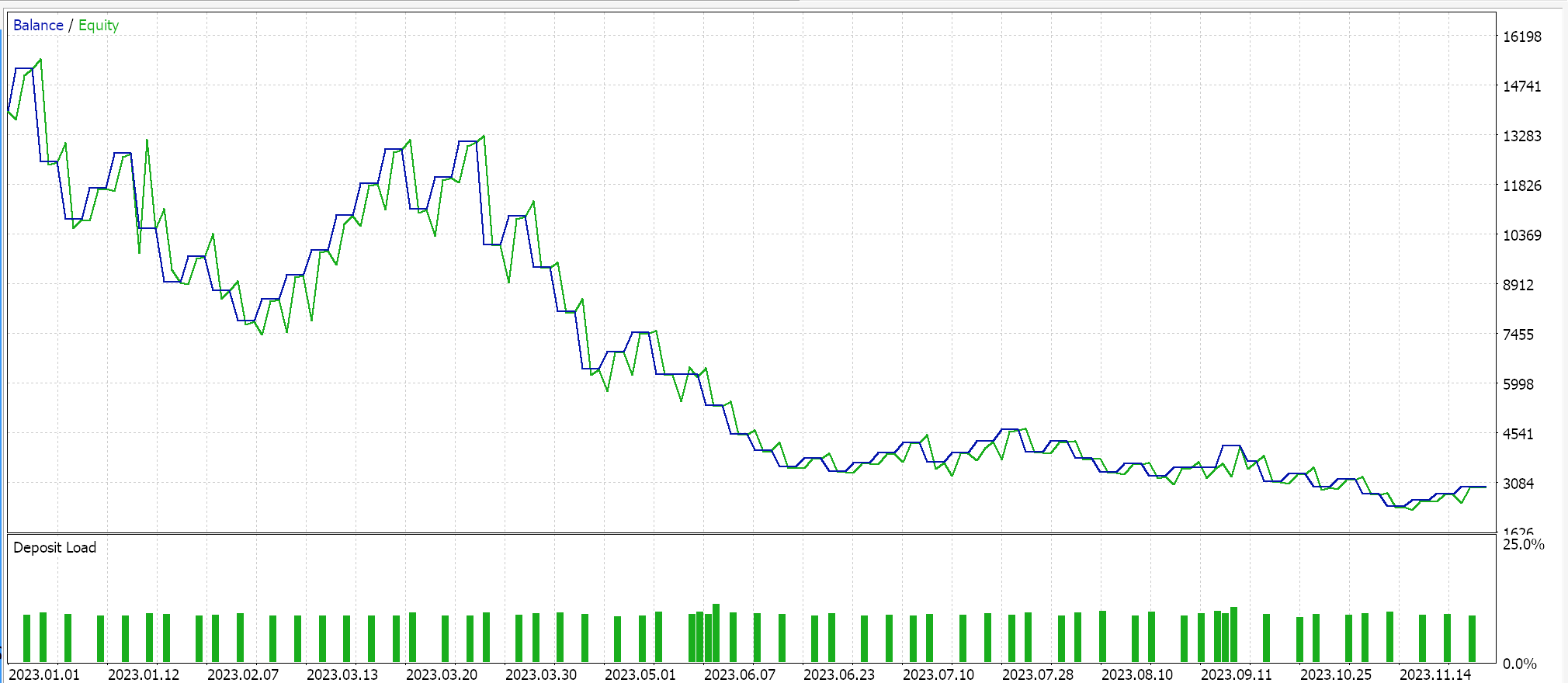
Conclusión

Entonces, para resumir nuestros hallazgos clave, la normalización por lotes requiere muchos parámetros y, por lo tanto, es costosa en términos de cálculo. Se debe tener especial cuidado al seleccionar los algoritmos de normalización a utilizar y, aunque la puntuación estándar es muy popular y común, tiene resultados no limitados que pueden generar gradientes muy grandes que obstaculizan la convergencia y ralentizan todo el proceso de entrenamiento. Sin embargo, si se utilizan algoritmos de normalización alternativos que tienen salidas limitadas como escalamiento de características o escalamiento robusto y estos se combinan con sus respectivas funciones de activación que tienen salidas limitadas similares, entonces el proceso de entrenamiento se puede acelerar. Lamentablemente, la velocidad es una consideración clave aquí porque, como ya se mencionó, la normalización por lotes involucra muchos parámetros y requiere un uso intensivo de recursos computacionales; por lo tanto, se debe tener especial cuidado al combinar algoritmos de normalización con funciones de activación, además de tener capas y tamaños de red óptimos.