Implementación en MQL5 de la prueba de Augmented Dickey-Fuller (ADF)

Introducción

La prueba Augmented Dickey-Fuller (ADF) es un procedimiento común utilizado para evaluar si una serie temporal es estacionaria o no. Aunque es bien sabido que las series temporales financieras son intrínsecamente no estacionarias. Muchos métodos estadísticos que se benefician de la estacionariedad suelen exigir que los conjuntos de datos no estacionarios se transformen de algún modo antes de ser analizados. La prueba ADF se puede utilizar para evaluar la eficacia de estas transformaciones en la inducción de estacionariedad. Alternativamente, para evaluar la cointegración de las series también se utilizan pruebas de estacionariedad. Útil en el desarrollo de estrategias de negociación que explotan las discrepancias en la fijación de precios de instrumentos financieros relacionados. En este artículo presentaremos la implementación del test ADF en MQL5 puro y demostraremos su aplicación utilizándolo para identificar símbolos cointegrados en MetaTrader 5.

Comprender la prueba ADF

En pocas palabras, una prueba ADF es una prueba de hipótesis que nos permite determinar si una característica específica de los datos observados es estadísticamente significativa. En este caso, la característica que se pretende determinar es la estacionariedad de una serie. Una hipótesis estadística es una suposición sobre un conjunto de datos representado por una muestra. Sólo podemos conocer la verdad real trabajando con el conjunto completo de datos. Lo cual no suele ser posible por una u otra razón. Así pues, se comprueba una muestra de un conjunto de datos para plantear una hipótesis de todo el conjunto de datos. Lo importante aquí es recordar que la veracidad de una hipótesis estadística nunca se conoce con certeza cuando se trabaja con muestras. Lo que obtenemos es si una suposición es probablemente cierta o falsa.

En una prueba ADF consideramos dos escenarios:

• La hipótesis nula de que existe una raíz unitaria en la serie temporal.

• La hipótesis alternativa es que la serie temporal no presenta una raíz unitaria.

En el análisis de series temporales, una raíz unitaria es una característica especial de un conjunto de datos secuenciales. Imagine a un hombre caminando por una calle con su perro. Es probable que el hombre camine en línea bastante recta hacia su destino. A menudo, el perro se aleja para olisquear algo o perseguir a algún bicho que le haya llamado la atención. Pero al final seguirá a su dueño. Si se traza la trayectoria del perro podemos observar algún tipo de oscilación. Donde el perro se aleja, pero finalmente vuelve a la dirección general esperada siendo seguido por el hombre.

Un punto arbitrario del recorrido del perro representa el valor de una variable en un momento determinado. Si evaluamos estos valores, es probable que se mantengan dentro de un determinado rango en torno a una tendencia central. Las propiedades estadísticas no cambian significativamente con el tiempo. Una serie de este tipo no tendrá raíz unitaria. Ahora imagina que el hombre pasease a su perro sin adiestrar por la misma calle. Lo más probable es que el perro salga corriendo y no vuelva con su dueño. Los valores asociados al camino que tome este perro variarán de forma impredecible. Una serie de este tipo tendrá una raíz unitaria.

La noción de raíz unitaria procede de la ecuación característica de un proceso estocástico. Un proceso estocástico es una secuencia de variables indexadas por el tiempo, que describe un sistema que evoluciona aleatoriamente. La ecuación característica de un proceso estocástico es una ecuación que capta las propiedades del sistema. La raíz unitaria es una solución de la ecuación característica igual a 1. Si un proceso tiene una raíz unitaria, significa que las perturbaciones o los efectos aleatorios tienen un efecto persistente en el proceso. Este sistema se modela mediante efectos aleatorios y valores retardados. Lo que significa que es de naturaleza autorregresiva.

Por lo tanto, la prueba ADF utiliza un modelo de regresión para comprobar si existe una raíz unitaria. La forma más común del modelo viene dada por la ecuación siguiente.

Dónde:

• "Y" - La primera diferencia de la serie temporal.
  

•  "a" - Un término constante.

•  "b" - El coeficiente del nivel retardado de la serie temporal.
  

•  "x" - El coeficiente de la tendencia temporal (t).

•  "V" - Coeficientes de las primeras diferencias retardadas.
  

•  "E" - El término de error.

La prueba se centra en el coeficiente "b". Si "b" = 0, existe una raíz unitaria; de lo contrario, si "b" < 0, la serie temporal es estacionaria. El estadístico ADF se calcula a partir del valor estimado de "b" y su error estándar. Se compara con los valores críticos de una distribución Dickey-Fuller. Si la estadística ADF es más negativa que el valor crítico en un nivel de significancia específico, se rechaza la hipótesis nula de una raíz unitaria. Significa que la serie es estacionaria.

Implementación

Para asegurarnos de que nuestra implementación es precisa utilizaremos como referencia una implementación existente de la prueba ADF en Python. En el paquete Python 'statsmodels', la función `adfuller` se utiliza para realizar una prueba ADF.

adfuller(x, maxlag: 'int | None' = None, regression='c', autolag='AIC', store=False, regresults=False)

La función estima en primer lugar los parámetros de un modelo autorregresivo de la serie de entrada utilizando mínimos cuadrados ordinarios. Se calcula una estadística de prueba basada en los parámetros estimados. Que se utiliza para calcular un valor "p". De una tabla de distribución se extraen tres valores críticos que representan niveles de confianza. Finalmente, la estadística de prueba puede ser comparada con cualquiera de estos valores para determinar si una serie es estacionaria o no.

A partir de esta visión de conjunto, hay tres componentes importantes que tenemos que aplicar. El primero es el modelo de regresión por mínimos cuadrados ordinarios. Probablemente el componente más importante, ya que cualquier error aquí se propagará a otras etapas de la prueba. Esto se utilizará para determinar el modelo autorregresivo más adecuado de la serie analizada. Además de los parámetros del modelo, también necesitamos calcular varias propiedades de un modelo, como su criterio de información de Akaike y su criterio de información bayesiano.

El segundo componente se refiere al cálculo del valor "p". El valor "p" viene determinado por el estadístico de prueba derivado del estadístico t del modelo autorregresivo óptimo. Una estadística "t" es una medida utilizada para determinar si existe una diferencia significativa entre las medias de dos grupos. Se calcula tomando la diferencia entre las medias muestrales y dividiéndola por el error típico de la diferencia. En este contexto, la estadística "t" se calcula dividiendo los parámetros del modelo por el error estándar del modelo. El método empleado para calcular el valor "p" fue propuesto por J.G. MacKinnon y por ello se denomina método del valor "p" aproximado de MacKinnon. Proporciona una aproximación al valor "p" asociado a los valores críticos de las pruebas estadísticas.

El último componente necesario para completar la prueba ADF es el cálculo de los valores críticos. Estos valores se derivan de aproximaciones dadas en un documento académico escrito por MacKinnon.

//+------------------------------------------------------------------+
//| Ordinary least squares class                                     |
//+------------------------------------------------------------------+
class OLS
  {
private:
   matrix m_exog,               //design matrix
          m_pinv,               //pseudo-inverse of matrix
          m_cov_params,         //covariance of matrix
          m_m_error,            //error matrix
          m_norm_cov_params;    //normalized covariance matrix
   vector m_endog,              //dependent variables
          m_weights,            //weights
          m_singularvalues,     //singular values of solution
          m_params,             //coefficients of regression model(solution)
          m_tvalues,            //test statistics of model
          m_bse,                //standard errors of model
          m_resid;              //residuals of model
   ulong  m_obs,                //number of observations
          m_model_dof,          //degrees of freedom of model
          m_resid_dof,          //degrees of freedom of residuals
          m_kconstant,          //number of constants
          m_rank;               //rank of design matrix
   double m_aic,                //Akiake information criteria
          m_bic,                //Bayesian information criteria
          m_scale,              //scale of model
          m_llf,                //loglikelihood of model
          m_sse,                //sum of squared errors
          m_rsqe,               //r-squared of model
          m_centeredtss,        //centered sum of squares
          m_uncenteredtss;      //uncentered sum of squares
   uint              m_error;              //error flag
   // private methods
   ulong             countconstants(void);
   void              scale(void);
   void              sse(void);
   void              rsqe(void);
   void              centeredtss(void);
   void              uncenteredtss(void);
   void              aic(void);
   void              bic(void);
   void              bse(void);
   void              llf(void);
   void              tvalues(void);
   void              covariance_matrix(void);


public:
   //constructor
                     OLS(void);
   //destructor
                    ~OLS(void);
   //public methods
   bool              Fit(vector &y_vars,matrix &x_vars);
   double            Predict(vector &inputs);
   double            Predict(double _input);
   //get properties of OLS model
   ulong             ModelDOF(void) { if(m_error) return 0; else return m_model_dof;}
   ulong             ResidDOF(void) { if(m_error) return 0; else return m_resid_dof;}
   double            Scale(void)  { if(m_error) return EMPTY_VALUE; else return m_scale;    }
   double            Aic(void)    { if(m_error) return EMPTY_VALUE; else return m_aic;      }
   double            Bic(void)    { if(m_error) return EMPTY_VALUE; else return m_bic;    }
   double            Sse(void)    { if(m_error) return EMPTY_VALUE; else return m_sse;    }
   double            Rsqe(void)   { if(m_error) return EMPTY_VALUE; else return m_rsqe;   }
   double            C_tss(void)  { if(m_error) return EMPTY_VALUE; else return m_centeredtss;}
   double            Loglikelihood(void) { if(m_error) return EMPTY_VALUE; return m_llf; }
   vector            Tvalues(void) { if(m_error) return m_m_error.Col(0); return m_tvalues; }
   vector            Residuals(void) { if(m_error) return m_m_error.Col(0); return m_resid; }
   vector            ModelParameters(void) { if(m_error) return m_m_error.Col(0); return m_params; }
   vector            Bse(void) { if(m_error) return m_m_error.Col(0);  return m_bse; }
   matrix            CovarianceMatrix(void) { if(m_error) return m_m_error; return m_cov_params; }
  };

OLS.mqh contiene la definición de la clase OLS, que representa un modelo de regresión por mínimos cuadrados ordinarios. La clase tiene varios métodos públicos. El primero de ellos es "Fit()", el primer método que los usuarios deben llamar después de crear una instancia de esta clase. Requiere como entrada un vector y una matriz. El vector "y_vars" debe rellenarse con los valores dependientes y "x_vars" es la matriz de diseño. "Fit()" devolverá true si se ejecuta correctamente, momento en el que podrá llamarse a cualquier otro método público. Todos estos métodos devuelven una propiedad específica de un modelo calculado. Estas propiedades se resumen en el cuadro siguiente.

Tipo de datos de retorno	Valor devuelto en caso de error	Método	Descripción
ulong	0	ModelDOF()	Los grados de libertad de un modelo.
ulong	0	ResidDOF()	Los grados de libertad de los residuos de un modelo.
double	EMPTY_VALUE	Scale()	Es la varianza del término de error, que indica la variabilidad de la variable dependiente no explicada por las variables independientes.
double	EMPTY_VALUE	Aic()	Criterios de información de Akaike.
double	EMPTY_VALUE	Bic()	Criterio de información bayesiano.
double	EMPTY_VALUE	Sse()	La suma de errores al cuadrado del modelo.
double	EMPTY_VALUE	Rsqe()	Es la métrica R-cuadrado (R²) del modelo, es decir, el coeficiente de determinación.
double	EMPTY_VALUE	C_tss()	Es la suma total de los errores al cuadrado centrados en la media.
double	EMPTY_VALUE	Loglikelihood()	La función de verosimilitud para el modelo OLS.
vector	vector of empty values	Tvalues()	Proporciona el estadístico "t" para la estimación de cada parámetro de un modelo.
vector	vector of empty values	Residuals()	Los residuos del modelo, es decir, la diferencia entre los valores previstos y los reales.
vector	vector of empty values	Bse()	Los errores estándar de las estimaciones de los parámetros.
matrix	matrix of empty values	CovarianceMatrix()	Matriz que muestra las varianzas de las variables y las covarianzas entre las variables.

 "Predict()" tiene dos sobrecargas que difieren por sus tipos de datos de entrada. Que son un vector o un valor escalar de tipo double. Ambos devuelven una única predicción dada(s) una(s) nueva(s) variable(s) independiente(s).

La siguiente parte de nuestra implementación se traslada al archivo ADF.mqh. Este archivo contendrá una colección de definiciones de funciones relacionadas con la prueba ADF. Una de estas funciones será "adfuller()". Incluimos OLS.mqh para la clase OLS, Math.mqh de la biblioteca estándar y también specialfunctions.mqh de la biblioteca Alglib.

//+------------------------------------------------------------------+
//|                                                          ADF.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\specialfunctions.mqh>
#include<OLS.mqh>

La siguiente parte de nuestra implementación se traslada al archivo ADF.mqh. Este archivo contendrá una colección de definiciones de funciones, así como la de la clase CAdf. Incluimos OLS.mqh para la clase OLS, Math.mqh de la biblioteca estándar y también specialfunctions.mqh de la biblioteca Alglib. ADF.mqh comienza con la definición de algunas enumeraciones. ENUM_INFO_CRIT representa las opciones disponibles a la hora de determinar el modelo de regresión óptimo para una serie concreta. Define las métricas utilizadas para seleccionar el modelo adecuado. ENUM_TRIM, ENUM_ORIGINAL, ENUM_HAS_CONST y ENUM_TREND se utilizan en la construcción de una matriz de diseño. 

//+------------------------------------------------------------------+
//| Information criterion                                            |
//+------------------------------------------------------------------+
enum ENUM_INFO_CRIT
  {
   INFO_NONE=0,
   INFO_AIC,
   INFO_BIC
  };
//+------------------------------------------------------------------+
//| Options for  trimming invalid observations                       |
//+------------------------------------------------------------------+
enum ENUM_TRIM
  {
   TRIM_NONE=0,
   TRIM_FORWARD,
   TRIM_BACKWARD,
   TRIM_BOTH
  };
//+------------------------------------------------------------------+
//| options for how to handle original data set                      |
//+------------------------------------------------------------------+

enum ENUM_ORIGINAL
  {
   ORIGINAL_EX=0,
   ORIGINAL_IN,
   ORIGINAL_SEP
  };
//+------------------------------------------------------------------+
//| Constant and trend used in regression model                      |
//+------------------------------------------------------------------+

enum ENUM_TREND
  {
   TREND_NONE=0,
   TREND_CONST_ONLY,
   TREND_LINEAR_ONLY,
   TREND_LINEAR_CONST,
   TREND_QUAD_LINEAR_CONST
  };
//+------------------------------------------------------------------+
//| Options for how to handle existing constants                     |
//+------------------------------------------------------------------+

enum ENUM_HAS_CONST
  {
   HAS_CONST_RAISE=0,
   HAS_CONST_SKIP,
   HAS_CONST_ADD
  };

El método "Adfuller()" de CAdf devuelve un valor booleano que significa que la prueba se ha ejecutado correctamente, NO LA ESTACIONARIEDAD DE UNA SERIE. Si se devuelve false debe haberse producido un error. Cualquier error irá acompañado de mensajes detallados en el diario del terminal. Toma como entrada un array de series a analizar. Otros argumentos de la función son opcionales. En la mayoría de los casos, los usuarios no tendrán que preocuparse por estos parámetros. Debería bastar con llamar a la función con los parámetros mencionados.

//+---------------------------------------------------------------------+
//|Class CAdf                                                           |
//|   encapsulates the the Augmented Dickey Fuller Test for Stationarity|
//+---------------------------------------------------------------------+

class CAdf
{
 private:
  double m_adf_stat,  //adf statistic
         m_bestic,    //optimal bic or aic
         m_pvalue;    //p-value
  ulong  m_usedlag;   //lag used for optimal reg model
  vector m_critvals;  //estimated critical values
  OLS    *m_ols;      //internal ordinary least squares reg model
   // private methods
 bool   gridsearch(vector &LHS, matrix &RHS, ulong f_lag, ulong l_lag,ENUM_INFO_CRIT crit, double &b_ic, ulong &best_lag);
 bool   lagmat(matrix &in,matrix &out[],ulong mlag,ENUM_TRIM trim=TRIM_BOTH,ENUM_ORIGINAL original=ORIGINAL_IN);
 bool   prepare_lhs_rhs(vector &lhs, matrix &rhs, double &in[], double &in_diff[],ulong lag);
 
 
 public:
  CAdf(void);
  ~CAdf(void);
  
 bool Adfuller(double &array[],ulong max_lag = 0,ENUM_TREND trend = TREND_CONST_ONLY, ENUM_INFO_CRIT autolag=INFO_AIC);
 vector CriticalValues(void) {  return m_critvals; }
 double AdfStatistic(void)   {  return m_adf_stat; }
 double Pvalue(void)         {  return m_pvalue;   }
};

"max_lag" define el número máximo de rezagos (lags) del modelo de regresión. "trend" es una enumeración que permite especificar la tendencia y la configuración constante del modelo de regresión. "autolag" determina qué métrica se utiliza para seleccionar el modelo óptimo que mejor describe la serie de entrada. Dentro de "Adfuller()", los parámetros de la función se comprueban primero antes de utilizarse para construir las variables dependientes e independientes de un modelo de regresión.

Se muestrean varias variaciones de esta matriz de diseño inicial para determinar cuál se ajusta mejor a la serie de entrada. El criterio utilizado para dar con el mejor modelo depende del valor del parámetro "autolag". La búsqueda se realiza mediante la función "gridsearch()".

Una vez que se encuentra el mejor modelo, la propiedad de retraso (lag) de este modelo, que se refiere al número de columnas incluidas desde la matriz de diseño inicial, se utiliza para definir el modelo óptimo. Cuyos parámetros se utilizarán para estimar la estacionariedad de la serie. La primera estadística "t" del modelo OLS óptimo define la estadística ADF de la prueba ADF. El valor "p" se calcula mediante la función "mackinnop()". Al llamar al método "Pvalue()" de CAdf se obtiene el valor "p" correspondiente.

//+----------------------------------------------------------------------+
//| calculates MacKinnon's approximate p-value for a given test statistic|
//+----------------------------------------------------------------------+
double mackinnonp(double teststat, ENUM_TREND trend = TREND_CONST_ONLY,ulong nseries = 1, uint lags =0)
  {
   vector small_scaling =  {1, 1, 1e-2};
   vector large_scaling =  {1, 1e-1, 1e-1, 1e-2};

   double tau_star_nc []= {-1.04, -1.53, -2.68, -3.09, -3.07, -3.77};
   double tau_min_nc []= {-19.04, -19.62, -21.21, -23.25, -21.63, -25.74};
   double tau_max_nc []= {double("inf"), 1.51, 0.86, 0.88, 1.05, 1.24};
   double tau_star_c []= {-1.61, -2.62, -3.13, -3.47, -3.78, -3.93};
   double tau_min_c []= {-18.83, -18.86, -23.48, -28.07, -25.96, -23.27};
   double tau_max_c []= {2.74, 0.92, 0.55, 0.61, 0.79, 1};
   double tau_star_ct []= {-2.89, -3.19, -3.50, -3.65, -3.80, -4.36};
   double tau_min_ct []= {-16.18, -21.15, -25.37, -26.63, -26.53, -26.18};
   double tau_max_ct []= {0.7, 0.63, 0.71, 0.93, 1.19, 1.42};
   double tau_star_ctt []= {-3.21, -3.51, -3.81, -3.83, -4.12, -4.63};
   double tau_min_ctt []= {-17.17, -21.1, -24.33, -24.03, -24.33, -28.22};
   double tau_max_ctt []= {0.54, 0.79, 1.08, 1.43, 3.49, 1.92};

   double tau_nc_smallp [][3]=
     {
        {0.6344, 1.2378, 3.2496},
        {1.9129, 1.3857, 3.5322},
        {2.7648, 1.4502, 3.4186},
        {3.4336, 1.4835, 3.19},
        {4.0999, 1.5533, 3.59},
        {4.5388, 1.5344, 2.9807}
     };

   double tau_c_smallp [][3]=
     {
        {2.1659, 1.4412, 3.8269},
        {2.92, 1.5012, 3.9796},
        {3.4699, 1.4856, 3.164},
        {3.9673, 1.4777, 2.6315},
        {4.5509, 1.5338, 2.9545},
        {5.1399, 1.6036, 3.4445}
     };

   double tau_ct_smallp [][3]=
     {
        {3.2512, 1.6047, 4.9588},
        {3.6646, 1.5419, 3.6448},
        {4.0983, 1.5173, 2.9898},
        {4.5844, 1.5338, 2.8796},
        {5.0722, 1.5634, 2.9472},
        {5.53, 1.5914, 3.0392}
     };

   double tau_ctt_smallp [][3]=
     {
        {4.0003, 1.658, 4.8288},
        {4.3534, 1.6016, 3.7947},
        {4.7343, 1.5768, 3.2396},
        {5.214, 1.6077, 3.3449},
        {5.6481, 1.6274, 3.3455},
        {5.9296, 1.5929, 2.8223}
     };



   double tau_nc_largep [][4]=
     {
        {0.4797, 9.3557, -0.6999, 3.3066},
        {1.5578, 8.558, -2.083, -3.3549},
        {2.2268, 6.8093, -3.2362, -5.4448},
        {2.7654, 6.4502, -3.0811, -4.4946},
        {3.2684, 6.8051, -2.6778, -3.4972},
        {3.7268, 7.167, -2.3648, -2.8288}
     };

   double tau_c_largep [][4]=
     {
        {1.7339, 9.3202, -1.2745, -1.0368},
        {2.1945, 6.4695, -2.9198, -4.2377},
        {2.5893, 4.5168, -3.6529, -5.0074},
        {3.0387, 4.5452, -3.3666, -4.1921},
        {3.5049, 5.2098, -2.9158, -3.3468},
        {3.9489, 5.8933, -2.5359, -2.721}
     };

   double tau_ct_largep [][4]=
     {
        {2.5261, 6.1654, -3.7956, -6.0285},
        {2.85, 5.272, -3.6622, -5.1695},
        {3.221, 5.255, -3.2685, -4.1501},
        {3.652, 5.9758, -2.7483, -3.2081},
        {4.0712, 6.6428, -2.3464, -2.546},
        {4.4735, 7.1757, -2.0681, -2.1196}
     };

   double tau_ctt_largep [][4]=
     {
        {3.0778, 4.9529, -4.1477, -5.9359},
        {3.4713, 5.967, -3.2507, -4.2286},
        {3.8637, 6.7852, -2.6286, -3.1381},
        {4.2736, 7.6199, -2.1534, -2.4026},
        {4.6679, 8.2618, -1.822, -1.9147},
        {5.0009, 8.3735, -1.6994, -1.6928}
     };


   vector maxstat,minstat,starstat;
   matrix tau_smallps, tau_largeps;

   switch(trend)
     {
      case TREND_NONE:
         if(!maxstat.Assign(tau_max_nc) ||
            !minstat.Assign(tau_min_nc) ||
            !starstat.Assign(tau_star_nc)||
            !tau_smallps.Assign(tau_nc_smallp)||
            !tau_largeps.Assign(tau_nc_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_CONST_ONLY:
         if(!maxstat.Assign(tau_max_c) ||
            !minstat.Assign(tau_min_c) ||
            !starstat.Assign(tau_star_c)||
            !tau_smallps.Assign(tau_c_smallp)||
            !tau_largeps.Assign(tau_c_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ct) ||
            !minstat.Assign(tau_min_ct) ||
            !starstat.Assign(tau_star_ct)||
            !tau_smallps.Assign(tau_ct_smallp)||
            !tau_largeps.Assign(tau_ct_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_QUAD_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ctt) ||
            !minstat.Assign(tau_min_ctt) ||
            !starstat.Assign(tau_star_ctt)||
            !tau_smallps.Assign(tau_ctt_smallp)||
            !tau_largeps.Assign(tau_ctt_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      default:
         Print(__FUNCTION__," Error invalid input for trend argument");
         return double("nan");
     }

   if(teststat>maxstat[nseries-1])
      return 1.0;
   else
      if(teststat<minstat[nseries-1])
         return 0.0;


   vector tau_coef;

   if(teststat<=starstat[nseries-1])
      tau_coef = small_scaling*(tau_smallps.Row(nseries-1));
   else
      tau_coef = large_scaling*(tau_largeps.Row(nseries-1));


   double rv,tau[];

   ArrayResize(tau,int(tau_coef.Size()));

   for(ulong i=0; i<tau_coef.Size(); i++)
      tau[i]=tau_coef[tau_coef.Size()-1-i];

   rv=polyval(tau,teststat);

   return CNormalDistr::NormalCDF(rv);
  }

Mientras que los valores críticos se calculan con "mackinnoncrit()". A cuyos resultados se puede acceder a través del método CAdf "CriticalValues()".

//+------------------------------------------------------------------+
//|Computes critical values                                          |
//+------------------------------------------------------------------+
vector mackinnoncrit(ulong nseries = 1,ENUM_TREND trend = TREND_CONST_ONLY, ulong num_obs=ULONG_MAX)
  {
   matrix tau_nc_2010 [] = {{
           {-2.56574, -2.2358, -3.627, 0},  // N [] = 1
           {-1.94100, -0.2686, -3.365, 31.223},
           {-1.61682, 0.2656, -2.714, 25.364}
        }
     };

   matrix tau_c_2010 [] =
     {
        {  {-3.43035, -6.5393, -16.786, -79.433},  // N [] = 1, 1%
           {-2.86154, -2.8903, -4.234, -40.040},   // 5 %
           {-2.56677, -1.5384, -2.809, 0}
        },        // 10 %
        {  {-3.89644, -10.9519, -33.527, 0},       // N [] = 2
           {-3.33613, -6.1101, -6.823, 0},
           {-3.04445, -4.2412, -2.720, 0}
        },
        {  {-4.29374, -14.4354, -33.195, 47.433},  // N [] = 3
           {-3.74066, -8.5632, -10.852, 27.982},
           {-3.45218, -6.2143, -3.718, 0}
        },
        {  {-4.64332, -18.1031, -37.972, 0},       // N [] = 4
           {-4.09600, -11.2349, -11.175, 0},
           {-3.81020, -8.3931, -4.137, 0}
        },
        {  {-4.95756, -21.8883, -45.142, 0},       // N [] = 5
           {-4.41519, -14.0405, -12.575, 0},
           {-4.13157, -10.7417, -3.784, 0}
        },
        {  {-5.24568, -25.6688, -57.737, 88.639},  // N [] = 6
           {-4.70693, -16.9178, -17.492, 60.007},
           {-4.42501, -13.1875, -5.104, 27.877}
        },
        {  {-5.51233, -29.5760, -69.398, 164.295},  // N [] = 7
           {-4.97684, -19.9021, -22.045, 110.761},
           {-4.69648, -15.7315, -5.104, 27.877}
        },
        {  {-5.76202, -33.5258, -82.189, 256.289},  // N [] = 8
           {-5.22924, -23.0023, -24.646, 144.479},
           {-4.95007, -18.3959, -7.344, 94.872}
        },
        {  {-5.99742, -37.6572, -87.365, 248.316},  // N [] = 9
           {-5.46697, -26.2057, -26.627, 176.382},
           {-5.18897, -21.1377, -9.484, 172.704}
        },
        {  {-6.22103, -41.7154, -102.680, 389.33},  // N [] = 10
           {-5.69244, -29.4521, -30.994, 251.016},
           {-5.41533, -24.0006, -7.514, 163.049}
        },
        {  {-6.43377, -46.0084, -106.809, 352.752},  // N [] = 11
           {-5.90714, -32.8336, -30.275, 249.994},
           {-5.63086, -26.9693, -4.083, 151.427}
        },
        {  {-6.63790, -50.2095, -124.156, 579.622},  // N [] = 12
           {-6.11279, -36.2681, -32.505, 314.802},
           {-5.83724, -29.9864, -2.686, 184.116}
        }
     };

   matrix tau_ct_2010 [] =
     {
        {  {-3.95877, -9.0531, -28.428, -134.155},   // N [] = 1
           {-3.41049, -4.3904, -9.036, -45.374},
           {-3.12705, -2.5856, -3.925, -22.380}
        },
        {  {-4.32762, -15.4387, -35.679, 0},         // N [] = 2
           {-3.78057, -9.5106, -12.074, 0},
           {-3.49631, -7.0815, -7.538, 21.892}
        },
        {  {-4.66305, -18.7688, -49.793, 104.244},   // N [] = 3
           {-4.11890, -11.8922, -19.031, 77.332},
           {-3.83511, -9.0723, -8.504, 35.403}
        },
        {  {-4.96940, -22.4694, -52.599, 51.314},    // N [] = 4
           {-4.42871, -14.5876, -18.228, 39.647},
           {-4.14633, -11.2500, -9.873, 54.109}
        },
        {  {-5.25276, -26.2183, -59.631, 50.646},    // N [] = 5
           {-4.71537, -17.3569, -22.660, 91.359},
           {-4.43422, -13.6078, -10.238, 76.781}
        },
        {  {-5.51727, -29.9760, -75.222, 202.253},   // N [] = 6
           {-4.98228, -20.3050, -25.224, 132.03},
           {-4.70233, -16.1253, -9.836, 94.272}
        },
        {  {-5.76537, -33.9165, -84.312, 245.394},   // N [] = 7
           {-5.23299, -23.3328, -28.955, 182.342},
           {-4.95405, -18.7352, -10.168, 120.575}
        },
        {  {-6.00003, -37.8892, -96.428, 335.92},    // N [] = 8
           {-5.46971, -26.4771, -31.034, 220.165},
           {-5.19183, -21.4328, -10.726, 157.955}
        },
        {  {-6.22288, -41.9496, -109.881, 466.068},  // N [] = 9
           {-5.69447, -29.7152, -33.784, 273.002},
           {-5.41738, -24.2882, -8.584, 169.891}
        },
        {  {-6.43551, -46.1151, -120.814, 566.823},  // N [] = 10
           {-5.90887, -33.0251, -37.208, 346.189},
           {-5.63255, -27.2042, -6.792, 177.666}
        },
        {  {-6.63894, -50.4287, -128.997, 642.781},  // N [] = 11
           {-6.11404, -36.4610, -36.246, 348.554},
           {-5.83850, -30.1995, -5.163, 210.338}
        },
        {  {-6.83488, -54.7119, -139.800, 736.376},  // N [] = 12
           {-6.31127, -39.9676, -37.021, 406.051},
           {-6.03650, -33.2381, -6.606, 317.776}
        }
     };

   matrix tau_ctt_2010 [] =
     {
        {  {-4.37113, -11.5882, -35.819, -334.047},  // N [] = 1
           {-3.83239, -5.9057, -12.490, -118.284},
           {-3.55326, -3.6596, -5.293, -63.559}
        },
        {  {-4.69276, -20.2284, -64.919, 88.884},    // N [] =2
           {-4.15387, -13.3114, -28.402, 72.741},
           {-3.87346, -10.4637, -17.408, 66.313}
        },
        {  {-4.99071, -23.5873, -76.924, 184.782},   // N [] = 3
           {-4.45311, -15.7732, -32.316, 122.705},
           {-4.17280, -12.4909, -17.912, 83.285}
        },
        {  {-5.26780, -27.2836, -78.971, 137.871},   // N [] = 4
           {-4.73244, -18.4833, -31.875, 111.817},
           {-4.45268, -14.7199, -17.969, 101.92}
        },
        {  {-5.52826, -30.9051, -92.490, 248.096},   // N [] = 5
           {-4.99491, -21.2360, -37.685, 194.208},
           {-4.71587, -17.0820, -18.631, 136.672}
        },
        {  {-5.77379, -34.7010, -105.937, 393.991},  // N [] = 6
           {-5.24217, -24.2177, -39.153, 232.528},
           {-4.96397, -19.6064, -18.858, 174.919}
        },
        {  {-6.00609, -38.7383, -108.605, 365.208},  // N [] = 7
           {-5.47664, -27.3005, -39.498, 246.918},
           {-5.19921, -22.2617, -17.910, 208.494}
        },
        {  {-6.22758, -42.7154, -119.622, 421.395},  // N [] = 8
           {-5.69983, -30.4365, -44.300, 345.48},
           {-5.42320, -24.9686, -19.688, 274.462}
        },
        {  {-6.43933, -46.7581, -136.691, 651.38},   // N [] = 9
           {-5.91298, -33.7584, -42.686, 346.629},
           {-5.63704, -27.8965, -13.880, 236.975}
        },
        {  {-6.64235, -50.9783, -145.462, 752.228},  // N [] = 10
           {-6.11753, -37.056, -48.719, 473.905},
           {-5.84215, -30.8119, -14.938, 316.006}
        },
        {  {-6.83743, -55.2861, -152.651, 792.577},  // N [] = 11
           {-6.31396, -40.5507, -46.771, 487.185},
           {-6.03921, -33.8950, -9.122, 285.164}
        },
        {  {-7.02582, -59.6037, -166.368, 989.879},  // N [] = 12
           {-6.50353, -44.0797, -47.242, 543.889},
           {-6.22941, -36.9673, -10.868, 418.414}
        }
     };

   vector ret_vector = {0,0,0};

   switch(trend)
     {
      case TREND_CONST_ONLY:
         process(tau_c_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_NONE:
         process(tau_nc_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_LINEAR_CONST:
         process(tau_ct_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_QUAD_LINEAR_CONST:
         process(tau_ctt_2010,ret_vector,num_obs,nseries);
         break;
      default:
         Print("Invalid input for trend argument");
         return ret_vector;
     }

   return ret_vector;
  }

Pruebas y validación

Para validar que nuestra implementación funciona correctamente realizaremos primero una prueba ADF en Python, sobre una serie aleatoria. A continuación, ejecutaremos la prueba ADF sobre la misma serie en Metatrader 5 y compararemos el resultado.

A continuación se muestra el código de la prueba ADF en Python.

import numpy as np
from statsmodels.tsa.stattools import adfuller

#initialize array with 100 elements
x = np.array([0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
              0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
              0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
              0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
              0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
              0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
              0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
              0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
              0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
              0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
              0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
              0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
              0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
              0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
              0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
              0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
              0.20684364,0.29630613,0.65178447,0.86559185])
   
#perform ADF test on array 
result = adfuller(x)

#print ADF statistic and p-value
print(f"ADF statistic: {result[0]}, p-value:{result[1]}")

#print critical values
print(f"Critical values:{result[4]}")
   

A continuación, ejecutamos la versión MQL5 de la prueba ADF en el mismo array, el código del programa script se muestra a continuación.

//+------------------------------------------------------------------+
//|                                                     ADF_test.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<ADF.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---series
   double rand_array[] =
     {
      0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
      0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
      0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
      0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
      0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
      0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
      0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
      0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
      0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
      0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
      0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
      0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
      0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
      0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
      0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
      0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
      0.20684364,0.29630613,0.65178447,0.86559185
     };

//---variables that will be used to store test results
   CAdf adf;
//--- Do ADF test
   if(adf.Adfuller(rand_array))
      Print("ADF test statistic: ", adf.AdfStatistic(), " P-value:", adf.Pvalue(),"\nCritical values \n",adf.CriticalValues());
   else
      Print("ADF test failed");
  }
//+------------------------------------------------------------------+

Ejecutando primero el script de Python:

LD      0       18:30:22.912    Test_adfuller (NFLX_us,Daily)   ADF statistic: -8.495443215534635, p-value:1.2796318143567197e-13
GJ      0       18:30:22.913    Test_adfuller (NFLX_us,Daily)   Critical values:{'1%': -3.4989097606014496, '5%': -2.891516256916761, '10%': -2.5827604414827157}

Y a continuación el script de MetaTrader 5. Podemos ver que los resultados son los mismos.

DO      0       18:30:48.460    ADF_test (NFLX_us,D1)   ADF test statistic: -8.495443215534634 P-value:1.2796318143567197e-13
ND      0       18:30:48.460    ADF_test (NFLX_us,D1)   Critical values 
OL      0       18:30:48.460    ADF_test (NFLX_us,D1)   [-3.49890976060145,-2.891516256916761,-2.582760441482716]

Cointegración

La correlación y la cointegración son conceptos estadísticos utilizados para medir las relaciones entre variables, especialmente en el contexto de los datos de series temporales. Aunque ambos miden las relaciones, sirven para fines distintos y se aplican en escenarios diferentes. La correlación es la medida estadística de la fuerza y la dirección de la relación lineal entre dos variables.

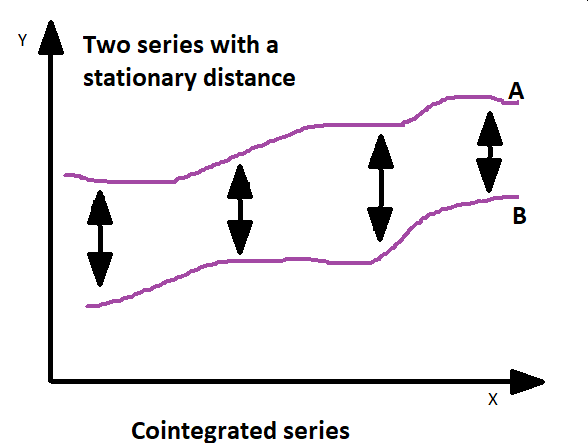
La cointegración, por su parte, se ocupa de la relación entre variables de series temporales no estacionarias que poseen un equilibrio a largo plazo o una relación estable. En términos más sencillos, identifica si existe una combinación de dos o más variables no estacionarias que tengan una relación estable a largo plazo cuando se consideran conjuntamente. La cointegración es útil para identificar pares de variables que se mueven juntas a lo largo del tiempo, a pesar de las fluctuaciones a corto plazo. Implica que las variables están vinculadas a largo plazo, lo que permite explotar esta relación para estrategias de negociación o modelización.

La cointegración suele evaluarse mediante pruebas estadísticas como la prueba de Engle-Granger o la prueba de Johansen. Estas pruebas comprueban si una combinación lineal de variables no estacionarias crea una serie estacionaria, lo que indica una relación a largo plazo. La prueba de Engle-Granger es un procedimiento de dos pasos para comprobar la cointegración entre dos variables en un entorno de series temporales. Consiste en estimar un modelo de regresión y realizar pruebas con los residuos para determinar si existe cointegración. Si se comprueba que los residuos del modelo de regresión son estacionarios, ello sugiere la existencia de cointegración entre las dos variables. En este caso, indica que a pesar de que las variables no son estacionarias individualmente, una combinación lineal de ellas sí lo es.

La prueba de Engle-Granger tiene la limitación de que no puede manejar varias secuencias simultáneamente. Esta limitación se aborda mediante la prueba de Johansen. Que es esencialmente una extensión del enfoque Engle-Granger para probar la cointegración entre múltiples series en un modelo autorregresivo vectorial. En este artículo no analizaremos la prueba de Johansen, ya que nos limitamos a tratar sólo dos series a la vez.

CointegrationTest.mqh contiene la clase de función CCoint. Implementa la prueba Engle-Granger aumentada con la ayuda de la clase CAdf. La prueba se realiza llamando al método "Aeg()" de CCoint. Se necesitan dos matrices de entrada que contengan las series que se van a probar. Los parámetros de entrada opcionales "trend", "max_lag", y "autolag", son similares a los parámetros del método "Adfuller()" en CAdf. De nuevo, para la mayoría de las pruebas los valores por defecto deberían ser suficientes. Como se demostrará en la sección siguiente. Los resultados de la prueba de cointegración se obtienen llamando a tres métodos de CCoint. El primero "CointStatistic", devuelve el estadístico ADF de la prueba ADF interna. "CriticalValues()" devuelve un vector de los valores críticos de la prueba. El valor "p" puede obtenerse llamando a "Pvalue()".

//+------------------------------------------------------------------+
//|                                            CointegrationTest.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<ADF.mqh>

//+------------------------------------------------------------------+
//|Class CCoint                                                      |
//|    implements cointegration test of two series                   |
//+------------------------------------------------------------------+
class CCoint
{
 private:
  double m_coint_stat;       //ADF test statistic
  double m_coint_pvalue;     //cointegration p-value
  vector m_coint_critvalues; //Cointegration critical values
  CAdf   *m_adf;             //CAdf object pointer
 public:
  CCoint(void);
  ~CCoint(void);
  
  bool Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC);
  
  double CointStatistic(void){ return m_coint_stat; }
  double Pvalue(void)        { return m_coint_pvalue;}
  vector CriticalValues(void){ return m_coint_critvalues;}
};
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CCoint::CCoint(void)
{
 m_adf = new CAdf();
 
 m_coint_critvalues = vector::Zeros(3);
 
 m_coint_stat=m_coint_pvalue=EMPTY_VALUE;
}
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CCoint::~CCoint(void)
{
 if(CheckPointer(m_adf)==POINTER_DYNAMIC)
     delete m_adf;
}
//+------------------------------------------------------------------+
//| Test for cointegration                                           |
//+------------------------------------------------------------------+
bool CCoint::Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC)
  {
//---  
   if(CheckPointer(m_adf)==POINTER_INVALID)
    {
     Print("Critical Internal error: Invalid CAdf pointer");
     return false;
    }
//---    
   if(in_one.Size()<1 || in_two.Size()<1 || in_one.Size()!=in_two.Size())
     {
      Print(__FUNCTION__," Invalid input for one or both arrays");
      return false;
     }

   vector y1,temp;
   matrix y2;

   if(!y1.Assign(in_one) || !temp.Assign(in_two) || !y2.Resize(temp.Size(),1) || !y2.Col(temp,0))
     {
      Print(__FUNCTION__," Assignment error: ", GetLastError());
      return false;
     }


   ulong obs,kvars=1;
   obs = y2.Rows();
   kvars++;
   matrix xx;

   if(trend==TREND_NONE)
     {
      if(!xx.Copy(y2))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }
     }
   else
    if(!addtrend(y2,xx,trend,false))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }

   OLS ols;

   if(!ols.Fit(y1,xx))
      return false;

   if(ols.Rsqe()< 1 - 100*SQRTEPS)
     {
      double resid[];

      vector resd = ols.Residuals();

      ArrayResize(resid,int(resd.Size()));

      for(uint i = 0; i<resid.Size(); i++)
         resid[i]=resd[i];

      if(!m_adf.Adfuller(resid,max_lag,TREND_NONE,autolag))
         return false;

      m_coint_stat = m_adf.AdfStatistic();
     }
   else
     {
      Print("They are (almost) perfectly collinear.\nCointegration test is not reliable in this case");
      m_coint_stat=double("nan");
     }

   if(trend==TREND_NONE)
      m_coint_critvalues.Fill(double("nan"));
   else
      m_coint_critvalues = mackinnoncrit(kvars,trend,obs-1);

   m_coint_pvalue = mackinnonp(m_coint_stat,trend,kvars);

   return true;
  }    

Probando símbolos para cointegración

Para la demostración final crearemos un script MQL5 que utiliza CCoint para comprobar la cointegración de una lista de símbolos. Los usuarios introducen una lista de símbolos, delimitados por comas. Establezca la fecha de inicio y la duración histórica de los precios de cierre a estudiar. "ConfidenceLevel" permite a los usuarios seleccionar el nivel de significación deseado. Esto determina el valor crítico que se comparará con la estadística ADF para el resultado final.

//+------------------------------------------------------------------+
//|                                    SymbolCointegrationTester.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <CointegrationTest.mqh>
//+------------------------------------------------------------------+
//| enumeration maps to confidence levels of 99%,95%, and 90%        |
//+------------------------------------------------------------------+
enum ENUM_CONFIDENCE_LEVEL
  {
   CONF_99=0,//99%
   CONF_95,//95%
   CONF_90 //90%
  };
//--- input parameters
input string   Symbols = "FB_us,GOOG_us,MSFT_us,NFLX_us,NVDA_us,AAPL_us,TSLA_us";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2022.01.01 00:00:01';
input int Size = 250;//History length
input ENUM_CONFIDENCE_LEVEL ConfidenceLevel=CONF_90;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(Size<100)
     {
      Print("Invalid input for Size");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;

//---in case there are less than two symbols specified
   if(num_symbols<2)
     {
      Print("Invalid input. Please list at least two symbols");
      return;
     }
//---output matrix of indices
   matrix sym_combos;
//---fill sym_combos with index values of symbols array
   PairedCombinations(symbols,sym_combos,num_symbols);
//---price arrays for pair of symbols
   double symA_prices [], symB_prices[];
//---output vectors holding results of cointegration test
   vector stats, critvals;
//---symbol pairs and result output
   string symA,symB,result;
//---CCoint object
   CCoint coint;
//---loop through all paired combinations from list
   for(ulong i=0; i<sym_combos.Rows(); i++)
     {
      //--- get symbol pair for current combination
      symA = symbols[int(sym_combos[i][0])];
      symB = symbols[int(sym_combos[i][1])];
      //--- get prices for the pair of symbols
      if(CopyClose(symA,TimeFrame,StartDate,Size,symA_prices)<Size||
         CopyClose(symB,TimeFrame,StartDate,Size,symB_prices)<Size)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //--- test the pair for cointegreation
      if(!coint.Aeg(symA_prices,symB_prices))
        {
         Print("Cointegration test failed ", ::GetLastError());
         return;
        }
      //---
      vector critvals = coint.CriticalValues();
      //--- prepare results output for a test
      if(coint.CointStatistic()<critvals[ConfidenceLevel])
         result="likely cointegrated.";
      else
         result="likely not cointegrated.";
      //--- output the result from cointegration test
      Print(symA," and ",symB, " are ", result);
     }
  }
//+------------------------------------------------------------------+
//| Combinations: generates paired combinations                      |
//+------------------------------------------------------------------+
bool PairedCombinations(string &in[], matrix &out,int count = 0)
  {
//---check input array
   if(in.Size()<1)
     {
      Print(__FUNCTION__," input array is empty");
      return false;
     }
//---set value for upto equal to the number of elements that should be
//---considered in the input array
   int upto = (count>1 && count<ArraySize(in))?count:ArraySize(in);
//--- calculate the number of rows equivalent to number of combinations
   ulong rows = ulong(MathFactorial(upto)/(MathFactorial(2)*MathFactorial(upto-2)));
//---resize output matrix accordingly
   out.Resize(rows,2);
//---fill output matrix with indexes of input array
   for(uint i=0,z=0; i<in.Size(); i++)
     {
      for(uint k = i+1; k<in.Size(); k++,z++)
        {
         out[z][0]=i;
         out[z][1]=k;
        }
     }
//---return
   return true;
  }
//+------------------------------------------------------------------+

En nuestro ejemplo probaremos los símbolos Google, Facebook, Microsoft, Netflix, Nvidia, Apple y Tesla. A continuación se muestran los resultados de la ejecución del script.

HN      0       18:37:31.239    SymbolCointegrationTester (NFLX_us,D1)  FB_us and GOOG_us are likely not cointegrated.
PQ      0       18:37:31.280    SymbolCointegrationTester (NFLX_us,D1)  FB_us and MSFT_us are likely not cointegrated.
IE      0       18:37:31.322    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NFLX_us are likely not cointegrated.
MG      0       18:37:31.365    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NVDA_us are likely not cointegrated.
PH      0       18:37:31.411    SymbolCointegrationTester (NFLX_us,D1)  FB_us and AAPL_us are likely not cointegrated.
NL      0       18:37:31.453    SymbolCointegrationTester (NFLX_us,D1)  FB_us and TSLA_us are likely not cointegrated.
EO      0       18:37:31.496    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and MSFT_us are likely not cointegrated.
ES      0       18:37:31.540    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NFLX_us are likely not cointegrated.
FE      0       18:37:31.582    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NVDA_us are likely not cointegrated.
CF      0       18:37:31.623    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and AAPL_us are likely not cointegrated.
EJ      0       18:37:31.665    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and TSLA_us are likely not cointegrated.
HM      0       18:37:31.705    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NFLX_us are likely not cointegrated.
RN      0       18:37:31.744    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NVDA_us are likely not cointegrated.
LP      0       18:37:31.785    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and AAPL_us are likely not cointegrated.
OD      0       18:37:31.825    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and TSLA_us are likely not cointegrated.
IG      0       18:37:31.866    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and NVDA_us are likely not cointegrated.
QI      0       18:37:31.906    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and AAPL_us are likely not cointegrated.
FP      0       18:37:31.946    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and TSLA_us are likely cointegrated.
EO      0       18:37:31.987    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and AAPL_us are likely not cointegrated.
RS      0       18:37:32.026    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and TSLA_us are likely not cointegrated.
DE      0       18:37:32.072    SymbolCointegrationTester (NFLX_us,D1)  AAPL_us and TSLA_us are likely not cointegrated.

Muestran que Netflix y Tesla están probablemente cointegrados con un nivel de confianza del 90%.

A continuación se muestra el código para realizar la misma prueba en Python, junto con los resultados.

"""
 Script demonstrates use of coint() from statsmodels
 to test symbols for cointegration
"""
# imports 
from statsmodels.tsa.stattools import coint
from itertools import combinations
from datetime import datetime
import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import pytz

#initialize connection to mt5
if not mt5.initialize():
    print("initialize() failed ")
    mt5.shutdown()
 
#set up timezone infomation   
tz=pytz.timezone("Etc/UTC")

#use time zone to set correct date for history data extraction
startdate = datetime(2022,1,1,hour=0,minute=0,second=1,tzinfo=tz)

#list the symbols 
Symbols = ["FB_us","GOOG_us","MSFT_us","NFLX_us","NVDA_us","AAPL_us","TSLA_us"]

#set length of data history
num_bars = 250

#set up the shape of the data structure to store prices 
data = np.zeros((num_bars,len(Symbols)))
prices = pd.DataFrame(data,columns=Symbols)

#fill prices dataframe with close prices
for symbol in Symbols:
    prices[symbol]=[rate[4]  for rate in mt5.copy_rates_from(symbol,mt5.TIMEFRAME_D1,startdate,num_bars)]
    
#we donot need mt5 from here 
mt5.shutdown()

#generate pairs from Symbols list 
pairs = list(combinations(prices.columns,2))

#set our desired significance level, 0.01->99%, 0.05->95%, 0.1->90%
confidence_level = 0.1

#do the test for cointegration on each pair and print results
for pair in pairs:
    df=prices[list(pair)]
    adf_stat,pvalue,critvalues=coint(df.values[:,0],df.values[:,1])
    if pvalue < confidence_level:
        print(pair[0]," and ",pair[1], " are likely cointegrated")
    else:
        print(pair[0]," and ",pair[1], " are likely not cointegrated")   

Resultados en Python

MR      0       18:35:17.835    SymbolCointegration (NFLX_us,Daily)     FB_us  and  GOOG_us  are likely not cointegrated
GE      0       18:35:17.851    SymbolCointegration (NFLX_us,Daily)     FB_us  and  MSFT_us  are likely not cointegrated
DI      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NFLX_us  are likely not cointegrated
CJ      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NVDA_us  are likely not cointegrated
MO      0       18:35:17.882    SymbolCointegration (NFLX_us,Daily)     FB_us  and  AAPL_us  are likely not cointegrated
JQ      0       18:35:17.898    SymbolCointegration (NFLX_us,Daily)     FB_us  and  TSLA_us  are likely not cointegrated
CD      0       18:35:17.914    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  MSFT_us  are likely not cointegrated
MF      0       18:35:17.930    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NFLX_us  are likely not cointegrated
QK      0       18:35:17.946    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NVDA_us  are likely not cointegrated
HM      0       18:35:17.962    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  AAPL_us  are likely not cointegrated
OO      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  TSLA_us  are likely not cointegrated
MS      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NFLX_us  are likely not cointegrated
PD      0       18:35:17.994    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NVDA_us  are likely not cointegrated
MF      0       18:35:18.010    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  AAPL_us  are likely not cointegrated
RJ      0       18:35:18.042    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  TSLA_us  are likely not cointegrated
RM      0       18:35:18.058    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  NVDA_us  are likely not cointegrated
GP      0       18:35:18.074    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  AAPL_us  are likely not cointegrated
LN      0       18:35:18.089    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  TSLA_us  are likely cointegrated
EF      0       18:35:18.105    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  AAPL_us  are likely not cointegrated
QI      0       18:35:18.121    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  TSLA_us  are likely not cointegrated
OJ      0       18:35:18.137    SymbolCointegration (NFLX_us,Daily)     AAPL_us  and  TSLA_us  are likely not cointegrated

Conclusión

Hasta ahora hemos visto la implementación de ADF (Augmented Dickey-Fuller) en MQL5 y lo hemos utilizado para implementar la prueba de Engle-Granger para la cointegración. La prueba ADF es una herramienta importante para los interesados en explorar estrategias de negociación de pares o arbitraje estadístico. Todo el código descrito en el artículo se incluye en el archivo ZIP. La siguiente tabla enumera todos los contenidos de este archivo.

Archivo	Descripción
Mql5\include\OLS.mqh	Contiene la definición de la clase OLS, que implementa la regresión por mínimos cuadrados ordinarios.
Mql5\include\ADF.mqh	Contiene la definición de varias funciones y la clase CAdf que implementa la prueba ADF.
Mql5\include\CointegrationTest.mqh	Define la clase CCoint que implementa una prueba de cointegración mediante la técnica Engle-Granger aumentada.
Mql5\scripts\ADF_test.mq5	Este es el script MQL5 utilizado para probar la implementación MQL5 de la prueba ADF.
Mql5\scripts\SymbolCointegrationTester.mq5	Script para probar símbolos en MetaTrader 5 para cointegración.
Mql5\scripts\Test_adfuller.py	Es un script Python que utiliza la implementación "statsmodels" de la prueba ADF utilizada para validar nuestra implementación MQL5.
Mql5\scripts\SymbolCointegration.py	Versión Python de SymbolCointegrationTester