Mieter - Seite 6
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Nein, nein. Nicht falsch. Hier ist die Abhängigkeit des Entnahmebetrags, die sich aus der iterativen Formel (in rot) und aus der analytischen Abhängigkeit (in blau) ergibt.
Sie können sehen, dass sie zusammenfallen und es ein Maximum in k gibt (auf der vorherigen Seite des Themas).
Natürlich gibt es keine diskreten Entnahmen, sondern zwangsläufig kontinuierliche Entnahmen zu gleichen Teilen. Es gibt also keine Lösung, in verschiedenen Zeiträumen unterschiedlich viel Geld abzuheben. Es gibt also keine Lösung, alles am Ende abzuziehen, ohne vorher abzuziehen. Dies ergibt sich nicht aus den Bedingungen des Problems, sondern aus den Formeln, die Sie anwenden (k ist fest, nicht variabel ki, i=0...T)
Abgezogene Mittel insgesamt
der Effekt wird spürbar, wenn die Wachstumsrate hoch genug ist
Ich habe ähnliche Abhängigkeiten.
Jetzt versuche ich, den Ausdruck für die Ableitung in Potenzen von k zu zerlegen, aber das ist nicht gut - ich muss sechs Größenordnungen berücksichtigen. Es ist klar, dass dies nicht analytisch gelöst werden kann. Vielleicht gibt es noch andere Ideen? Jemand erwähnte Diphurken...
Ich habe ähnliche Abhängigkeiten.
Jetzt versuche ich, den Ausdruck für die Ableitung in Potenzen von k zu zerlegen, aber das ist nicht gut - ich muss sechs Größenordnungen berücksichtigen. Es ist klar, dass dies nicht analytisch gelöst werden kann. Vielleicht gibt es noch andere Ideen? Jemand erwähnte Diphurken...
Das ist analytisch ein bisschen kompliziert. Zu q und t. Es kommt irgendwie auf die Art und Weise an :) Mit zunehmendem q und zunehmendem t nimmt der Anteil der optimalen Entfernung stetig ab
Ich habe ähnliche Abhängigkeiten.
Jetzt versuche ich, den Ausdruck für die Ableitung in Potenzen von k zu zerlegen, aber das ist nicht gut - ich muss sechs Größenordnungen berücksichtigen. Es ist klar, dass dies nicht analytisch gelöst werden kann. Vielleicht gibt es noch andere Ideen? Jemand erwähnte Diphurken...
Sie können vom Besonderen zum Allgemeinen übergehen. Wenn zum Beispiel t = 1 ist, können Sie nur einmal Geld abheben und müssen es daher in Höhe von q abheben. Betrachten Sie dann den Fall für t = 2, t = 3 usw.
D.h. wenn es bei t = 2 optimal ist, weniger als q auf einmal abzuheben, dann findet man ein Extremum und verallgemeinert für alle q bei t = 2.
Ähnliches gilt für t = 3, t = 4 usw.
Aus dem Wert des Extremwerts lässt sich die Größe der Entnahme als f(t)
Für den nachgeschalteten Anwender kann ein verbundenes Schiffssystem in Betracht gezogen werden.
Anfangsvolumen des ersten Gefäßes B0
Sie können vom Besonderen zum Allgemeinen übergehen. Wenn zum Beispiel t = 1 ist, können Sie nur einmal Geld abheben und müssen daher einen Betrag von q abheben. Betrachten Sie dann den Fall für t = 2, t = 3 usw.
Aus dem Wert des Extremwerts können wir die Größe der Rücknahme als f(t) ermitteln
Sie könnten Recht haben. Abgesehen davon, dass wir für t = 3 bereits gemäß der Gleichung
Grad k - drei in der ersten Ableitung df(k)/dk=0 haben, und wir nach Wurzeln der kubischen Gleichung mit allem, was sie impliziert, suchen müssen... Das heißt, dass wir in diesem Szenario nicht weiter als bis t=3 kommen können. Es sei daran erinnert, dass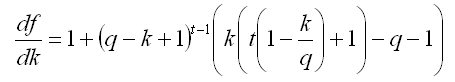 
und für t=1 optimale Größe k=q, für t=2 k=q, für t=3 k=q. Aber t weiter zu erhöhen und analytisch zu lösen, funktioniert nicht. Eine numerische Lösung zeigt, dass bei einer Einlagenwachstumsrate q von bis zu 10 % pro Monat die optimale Entnahmerate bei t>30 Monaten niedriger als q ist.
Daraus folgt: Wenn die TS-Zuverlässigkeit so beschaffen ist, dass die durchschnittliche Lebensdauer der Einlage 3 Jahre nicht überschreitet, dann ist das optimale Verhalten eine monatliche Entnahme des gesamten Gewinns (die Einlage wächst nicht). Andernfalls müssen wir eine analytische Lösung für den optimalen Entnahmeprozentsatz k finden und nach der Formel vorgehen. Dieses Szenario garantiert ein maximales Taschengeld während der voraussichtlichen Laufzeit der Einlage.
Um DU zu machen, können wir das Schema der verbundenen Gefäße betrachten: Anfangsvolumen des ersten Gefäßes B0
Wenn sich die Gefäße (Flüssigkeitsstrom) im dynamischen Gleichgewicht befinden (d. h. wie viel Flüssigkeit pro Zeiteinheit in das erste Gefäß hineinfließt, so viel fließt aus dem letzten heraus), ist das Problem des Wasserstands in jedem Gefäß elementar gelöst und wird nicht auf das Ablagerungsproblem reduziert. Wenn man Gefäße im Prozess ihrer Füllung betrachtet, ist die Analogie mit der Ablagerung nicht klar. avtomat ,erklären Sie bitte, was Sie meinten, indem Sie eine solche Interpretation vorschlagen?
P.S. Der Appell, eine annähernde analytische Lösung der Gleichung df/dk=0 zu erhalten, gilt nach wie vor. Jede Idee ist willkommen.