[Archiv!] Reine Mathematik, Physik, Chemie usw.: Gehirntrainingsprobleme, die in keiner Weise mit dem Handel zusammenhängen - Seite 614
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Dima, warum willst du wissen, wie hoch die Wahrscheinlichkeit ist, dass sie um Tausendstel eines Prozents von eins abweicht? Wenn Sie Garantien wollen, es gibt keine. Nobelpreisträger (LTCM) und Niederhoffer selbst versteckten sich hinter Wahrscheinlichkeiten bis zu einem gewissen Grad minus eins - und "trafen" trotzdem.
Und sehr kleine Wahrscheinlichkeiten (sehr groß) werden verwendet, um die ungefähre Lebensdauer des Systems zu berechnen. Es ist wichtig zu wissen, wie lange es dauern wird - ein Jahr oder 10 Jahre.
Gibt es etwas, auf das man sich verlassen kann? Mathematik ist der beste Weg.
Richtig?
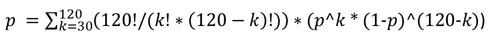
Das ist richtig!
Aber Rundungsfehler können die gesamte Genauigkeit zunichte machen. Es ist besser, die Summe von 0 bis 30 zu zählen. Sie ist gleich der Addition zur gewünschten Wahrscheinlichkeit.
Es gibt Fälle, in denen die Summe der Flächen gleich 17 ist.
Zum Beispiel, (333332) > (662111), mit einer Gewinnwahrscheinlichkeit von 23/36 ~ 0,64. Zugegeben, einfach ist das nicht: (662111) gewinnt nicht mit nennenswertem Vorsprung.
Es scheint, dass bisher die Summe der 18 Gesichter am fruchtbarsten ist.
Wenn wir die Kugeln zurückgeben, dann ist es immer p=q, so dass wir die Formel auf der rechten Seite vereinfachen können (* p^120)
Es ist eigentlich egal, ob wir zurückkehren oder nicht. Wir holen zu wenig heraus, um etwas zu bewirken. Aber es lässt sich anständig vereinfachen. Und in Klammern mit Potenzen bleibt der Multiplikator (1/2)^120.
Hehe.
2 Dima: Lassen Sie sich nicht auf diese Kombinationen ein. Machen Sie sich mit der Normalverteilung vertraut und bilden Sie ein definitives Integral von Null bis zur unteren Grenze, die Ihrer 30 entspricht. Sie werden einen großen Fehler mit Kombinationen in dieser Formel machen, es sei denn, Sie finden eine analytische Formel für die einfache Summe von Kombinationen.
Oder versuchen Sie die Summe der Kombinationen von 0 bis 30, die p-Noten werden Sie nicht stören. Vielleicht haben Sie Glück.
P.S. Kurz gesagt, es ist ganz einfach. Siehe hier.
Sie müssen k1, k2 und dann das Integral berechnen.
Nehmen wir k1=0, k2=30, das ist genauer. n=120, p=q=1/2. Dann
(k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5,477
(k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10,954.
Auch 1/sqrt(2*pi) ~ 0,39894 ist nützlich.
Setzt man die ersten beiden Zahlen in die Integrationsgrenzen ein und setzt 0,39894*exp(-x^2/2) in die Integrandenfunktion ein, so erhält man (hier ein Service zur Bildung bestimmter Integrale):
2.163*10^(-8).
Ihre Wahrscheinlichkeit ist also 1-2,163*10^(-8) ~ 0,99999998.
Versuchen Sie gar nicht erst, den Anfang der Funktion unter dem Integral zu nehmen: Er ist nicht ganzzahlig.