[Archiv!] Reine Mathematik, Physik, Chemie usw.: Gehirntrainingsprobleme, die in keiner Weise mit dem Handel zusammenhängen - Seite 304
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
F(1/y, 1/x) = min( 1/y, 1/x + y, x ) = F(x,y).
Daher ändert sich das Minimum nicht, wenn Sie y durch 1/x und x durch 1/y ersetzen. Y = 1/x.
Also F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x ). Sie ist gleich x, wenn x < sqrt(2), und 2/x andernfalls.
Zeichne die beiden Kurven y=x und y=2/x. Offensichtlich liegt das Maximum genau im Schnittpunkt der beiden Punkte und ist gleich sqrt(2).
Die Lösung im Problembuch ist ziemlich vage, das gefällt mir nicht:
Nächste (8.):
Dieser Teil ist trivial aufgebaut. Lassen wir die Intrigen hinter uns.
Der zweite Teil des Problems (ebenfalls 8.):
Die Abbildung wurde vereinfacht:
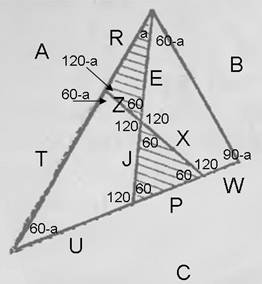
Richie, wie kommt es, dass die Winkel in dem schattierten Dreieck gleich sind?
Übrigens sagt die Aufgabenstellung nichts darüber aus, ob das ursprüngliche Dreieck gleichseitig ist. Obwohl es wie ein gleichseitiges gezeichnet ist.
Na los! Beweisen Sie es.
-
Jedenfalls war die Idee die folgende:
Der Flächeninhalt eines 4x-Dreiecks ist gleich einem Drittel der Differenz der Flächeninhalte des großen Dreiecks und der 4 kleinen Dreiecke, also 4 cm².
Um den Flächeninhalt des großen Dreiecks zu bestimmen, muss man seine Seite (in der Abbildung - A) ermitteln.
Ermitteln Sie die Seite des mittleren Dreiecks nach der Fläche. Es ist kein Problem zu wissen, dass es gleichseitig ist, denn sie ist gleich sqr(4*S/sqr(3)).
В центральном? Это очевидно.
Nur wenn die drei Dreiecke (außer dem mittleren) gleich sindAber das ist keine Tatsache, wenn man die Bedingungen betrachtet
Es muss etwas geben, an dem man sich festhalten kann. Es gibt eine Spur, aber ich weiß noch nicht, was ich damit anfangen soll.
Nur wenn die drei Dreiecke (außer dem mittleren) identisch sind.
Aber das ist keine Tatsache.
Nun, Sie haben mich völlig verwirrt.
Ich dachte, das große Dreieck sei gleichseitig. Die kleinen 3 Dreiecke sind gleichseitig, daher sind sie ähnlich.