Klassische Strategien neu interpretieren (Teil III): Prognose von höhere Hochs und tiefere Tiefs

Einführung

Künstliche Intelligenz bietet möglicherweise unendlich viele Möglichkeiten, unsere Handelsmöglichkeiten zu verbessern. Es ist jedoch unwahrscheinlich, dass alle Strategien wirksam sind. Unser Ziel ist es, den Händlern zu helfen, die Strategien zu finden, die ihren Bedürfnissen am besten entsprechen, indem wir die notwendigen Informationen für eine fundierte Entscheidungsfindung bereitstellen.

Angesichts der großen Anzahl möglicher Strategiekombinationen kann kein einzelner Händler sie alle umfassend bewerten, bevor er wichtige Entscheidungen trifft. Dieses Problem wird von allen Mitgliedern unserer Handelsgemeinschaft geteilt. Daher werden wir in dieser Artikelserie den Suchraum der Handelsstrategien erkunden, indem wir die Genauigkeit beliebter Strategien mit den einfachsten Modellen vergleichen.

In diesem Artikel nehmen wir die klassische Price-Action-Trading-Strategie des Handels auf der Grundlage von „höheren Hochs“ oder „tieferen Tiefs“ unter die Lupe. Wir haben verschiedene Modelle trainiert, um zwei verschiedene Ziele vorherzusagen. Das erste Ziel war die Vorhersage von Preisveränderungen, das einfachste Ziel überhaupt. Mit dem zweiten Ziel sollte ermittelt werden, ob der künftige Schlusskurs über dem aktuellen Höchststand, unter dem aktuellen Tiefststand oder zwischen den beiden Werten liegen würde.

Um Modelle unterschiedlicher Komplexität zu vergleichen, haben wir eine Zeitreihen-Kreuzvalidierung ohne zufälliges Mischen durchgeführt. Wir analysierten die Veränderungen in den Genauigkeitswerten für beide Ziele. Unsere Ergebnisse deuten darauf hin, dass einfachere Modelle, die Änderungen des Preisniveaus vorhersagen, effektiver sein könnten.

Überblick über die Handelsstrategie

Wenn Händler, die Preisaktionsstrategien verfolgen, ein Wertpapier analysieren, suchen sie in der Regel nach Anzeichen für starke Trends, die sich entweder bilden oder abklingen. Ein bekanntes Zeichen für die Bildung eines starken Trends ist es, wenn die Kurse über früheren Extremwerten schließen und in immer größeren Schritten weiter abdriften. Dies wird umgangssprachlich als „höhere Hochs“ oder „tiefere Tiefs“ bezeichnet, je nachdem, in welche Richtung sich der Kurs bewegt.

Seit zahllosen Generationen nutzen Händler diese einfache Strategie, um Einstiegs- und Ausstiegspunkte zu identifizieren. Ausstiegspunkte werden in der Regel dann festgelegt, wenn der Kurs seine Extremwerte nicht durchbricht, was darauf hindeutet, dass der Trend an Stärke verliert und sich möglicherweise umkehren wird. Im Laufe der Jahre wurden verschiedene kleinere Erweiterungen an dieser Strategie vorgenommen, aber das Grundmuster ist das gleiche geblieben.

Einer der größten Nachteile dieser Strategie besteht darin, dass der Kurs unerwartet unter sein Extrem zurückfällt. Diese nachteiligen Kursänderungen werden als „Retracements“ (Rücksetzer) bezeichnet und sind schwer vorherzusagen. Folglich gehen die meisten Händler nicht sofort eine Position ein, wenn der Kurs ein neues Extrem erreicht. Stattdessen warten sie ab, wie lange der Kurs diese Niveaus halten kann, bevor sie sich festlegen — und damit dem Trend die Möglichkeit geben, sich zu bewähren. Dieser Ansatz wirft jedoch mehrere Fragen auf: Wie lange sollte man warten, bevor man zu dem Schluss kommt, dass sich der Trend bewährt hat? Umgekehrt: Wie lange ist zu lange, bis sich der Trend umkehrt? Dies ist das Dilemma, vor dem Preisaktionsanalysten stehen.

Überblick über die Methodik

Da wir nun die Schwächen der Handelsstrategie kennen, verstehen wir auch die Motivation, die hinter dem Einsatz von KI zur Überwindung dieser bisherigen Einschränkungen steht. Wie bereits erwähnt, haben wir eine Reihe von Klassifikatoren trainiert, um vorherzusagen, ob der Kurs über seine aktuellen Extremwerte hinaus schließen oder innerhalb der Spanne bleiben würde. Für diese Aufgabe haben wir verschiedene Klassifikatoren ausgewählt, darunter AdaBoost, Entscheidungsbäume und neuronale Netze. Vor dem Vergleich wurde bei keinem der Modelle eine Abstimmung der Hyperparameter vorgenommen.

Wir ordneten die drei möglichen Ergebnisse drei kategorialen Ebenen zu: 1, 2 bzw. 3:

• 1 bedeutet, dass der Schlusskurs in der Zukunft höher sein wird als das gegenwärtige Hoch
• 2 bedeutet, dass der Schlusskurs in der Zukunft tiefer sein wird als der derzeitige Tief
• 3 bedeutet, dass 1 und 2 falsch waren, der zukünftige Preis wird zwischen dem aktuellen Hoch und Tief liegen.

Es sei darauf hingewiesen, dass das neue Ziel, das wir geschaffen haben, schwieriger zu interpretieren ist. Wenn unser Modell einen Übergang zu Zustand 3 vorhersagt, kann es ungewiss bleiben, ob das Preisniveau steigen oder sinken wird, je nach dem, wie hoch der Preis zu diesem Zeitpunkt ist. Das macht unser Modell nicht nur weniger transparent, sondern auch scheinbar weniger genau als das einfachste Modell.

Normalerweise zeichnen wir jede Strategie aus, die das einfachste Modell übertreffen kann. Eine komplexe Strategie, der dies nicht gelingt, rechtfertigt möglicherweise nicht den zusätzlichen Einsatz begrenzter Ressourcen, wie etwa Zeit.

Explorative Datenanalyse in Python

Zunächst müssen wir die Marktdaten aus unserem MetaTrader 5 Terminal exportieren. Zunächst öffnen wir das Terminal und wählen das Symbol-Icon. Dann wählen wir aus dem Kontextmenü die Option Balken, suchen das gewünschte Symbol und drücken dann auf Exportieren.

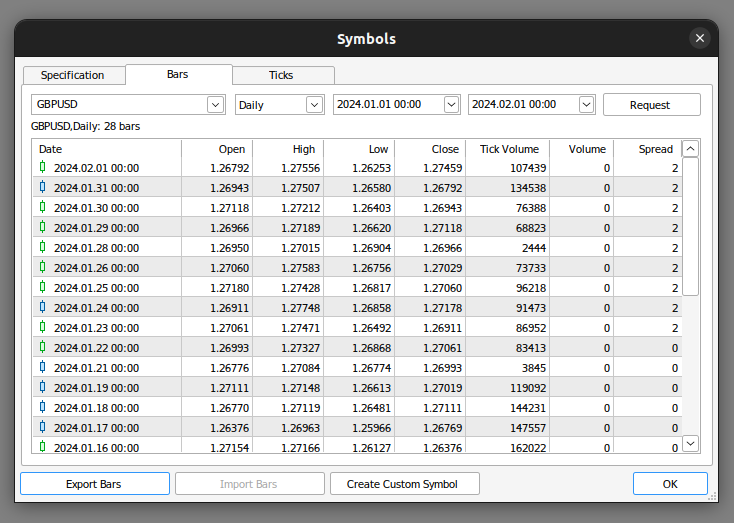
Abb. 1: Vorbereitung für den Export von Marktdaten

Nun, da unsere Daten fertig sind, können wir damit beginnen, zu visualisieren, ob es irgendwelche Beziehungen zwischen den fraglichen Variablen gibt.

Wir beginnen mit dem Import der benötigten Bibliotheken.

#import libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

Dann lesen wir die Daten ein, die wir zuvor vorbereitet haben. Beachten Sie, dass das MetaTrader 5-Terminal uns csv-Dateien liefert, die durch Tabs getrennt sind. Daher übergeben wir beim Einlesen der Datei den Parameter „\t“.

gbpusd = pd.read_csv("/home/volatily/market_data/GBPUSD_Daily_20160103_20240131.csv",sep="\t")

Wie geben den Spalten in unserem Datenrahmen neue Namen.

#Rename the columns
gbpusd.rename(columns={"<DATE>":"Date","<OPEN>":"Open","<HIGH>":"High","<LOW>":"Low","<CLOSE>":"Close","<TICKVOL>":"TickVol","<VOL>":"Vol","<SPREAD>":"Spread"},inplace=True)

Legen wir fest, wie weit wir in die Zukunft vorausschauen wollen.

#Define how far into the future we want to forecast
look_ahead = 20

Jetzt werden wir unsere Etiketten auf die gleiche Weise definieren, wie wir es besprochen haben.

#This column will help us with our plots
gbpusd["Future Close"] = gbpusd["Close"].shift(-look_ahead)
#Let's mark the normal target
#If price rises, our target will be 1
#If price falls, our target will be 0
gbpusd["Price Target"] = 0
#Let's mark the new target
#If price makes a higher high, we will label 1
#If price makes a lower low, we will label 2
#If price fails to make either, we will label 3
gbpusd["New Target"] = 0

Kennzeichnung der Daten.

#Labeling the data
#If the future close was less than the current close, price depreciated, label 0
gbpusd.loc[gbpusd["Close"] > gbpusd["Close"].shift(-look_ahead),"Price Target"] = 0
#If the future close was greater than the current close, price depreciated, label 1
gbpusd.loc[gbpusd["Close"] < gbpusd["Close"].shift(-look_ahead),"Price Target"] = 1
#If price makes a higher high our label will be 1
gbpusd.loc[gbpusd["Close"].shift(-look_ahead) > gbpusd["High"],"New Target"] = 1
#If price makes a lower low our label will be 2
gbpusd.loc[gbpusd["Close"].shift(-look_ahead) < gbpusd["Low"],"New Target"] = 2
#Otherwise our label will be 3 
gbpusd.loc[gbpusd["Close"].shift(-look_ahead) < gbpusd["Low"],"New Target"] = 3

Wir können alle Zeilen mit fehlenden Werten löschen.

#Drop the last look ahead rows
gbpusd = gbpusd[:-look_ahead]

Die Handelsstrategie setzt voraus, dass es eine Beziehung zwischen dem Schlusskurs und dem Hoch gibt. Lassen Sie uns sehen, ob es eine Beziehung zwischen dem Schlusskurs und dem Hoch gibt.

#Plot a scattor plot so we can see if there may be any relationship between the close and the high
sns.scatterplot(data=gbpusd,x="Close",y="High",hue="Price Target")

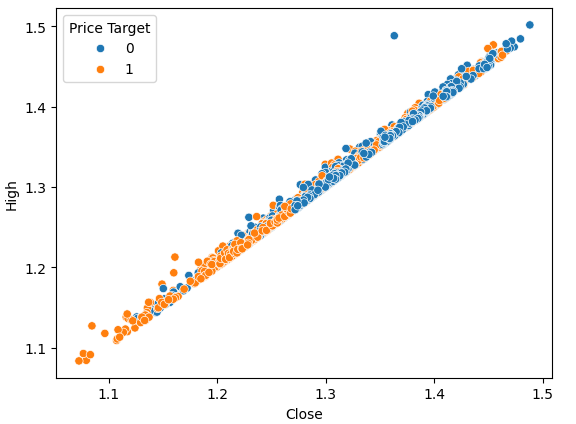
Abb. 2: Visualisierung des Schlusskurses im Vergleich zu den Hochs

Streudiagramme sind hilfreich, da sie es uns ermöglichen, die Beziehungen zwischen beliebigen Paaren von Zustandsvariablen in dem von uns modellierten System zu visualisieren.

Bei der Betrachtung der Daten können wir sofort eine starke, fast lineare Beziehung zwischen dem Schlusskurs und dem Höchstkurs erkennen. Wir haben das Diagramm eingefärbt, um die Fälle, in denen der Preis gestiegen ist, von denen zu unterscheiden, in denen er gesunken ist. Wie bereits festgestellt, gibt es keine klare Trennung zwischen den beiden Instanzen. Die einzigen auffälligen Trennungspunkte treten bei extremen Werten auf; wenn der Kurs beispielsweise unter der Marke von 1,1 schließt, scheint er immer wieder abzuspringen.

Wir können dasselbe Streudiagramm erstellen, aber dieses Mal setzen wir den niedrigen Preis auf die y-Achse.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Low",hue="Price Target")

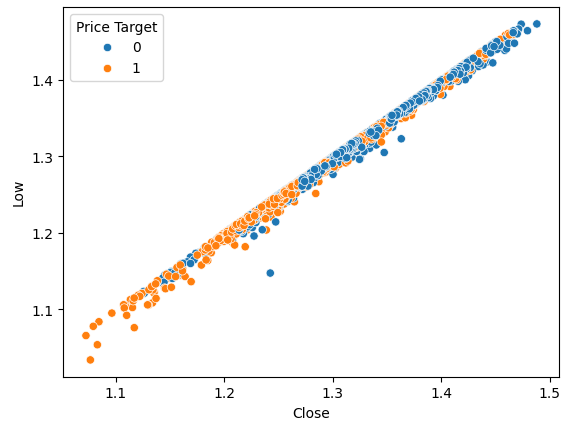
Abb. 3: Visualisierung des Verhältnisses zwischen den Schlusskursen und dem Tiefstkursen

Wie erwartet, ist die natürliche Trennung nicht sehr ausgeprägt. Diese natürliche Trennung ist erwünscht, weil sie unseren Modellen hilft, Entscheidungsgrenzen schneller zu lernen. Wir wollen sehen, ob unser neues Ziel uns hilft, unseren Datensatz besser zu trennen.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Low",hue="New Target")

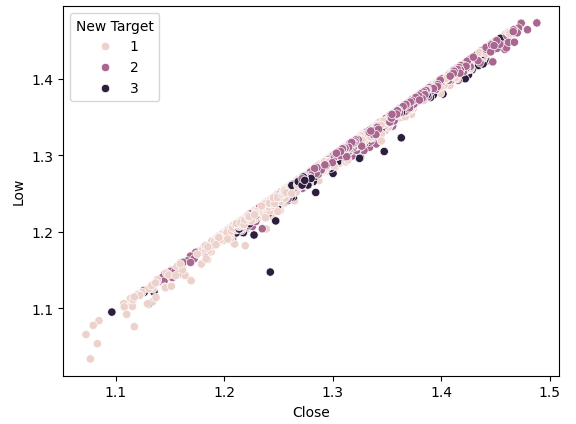
Abb. 4: Unser neues Ziel führt nicht zu mehr Trennung

Wie wir sehen können, ist die Trennung immer noch schlecht. Die dunkelsten Punkte, die den Zustand 3 repräsentieren, erstrecken sich fast über die gesamte Länge unseres Diagramms. Dies ist problematisch, weil es visuell darauf hinweist, dass es in unseren Daten Fälle gibt, in denen dieselbe Eingabe zu unterschiedlichen Ergebnissen führt.

Um zu veranschaulichen, wie eine gute Trennung aussieht, stellen wir den aktuellen Preis auf der x-Achse und den zukünftigen Preis auf der y-Achse dar. Wir färben die Diagrammpunkte orange für Preissteigerungen und blau für Preissenkungen.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Future Close",hue="Price Target")

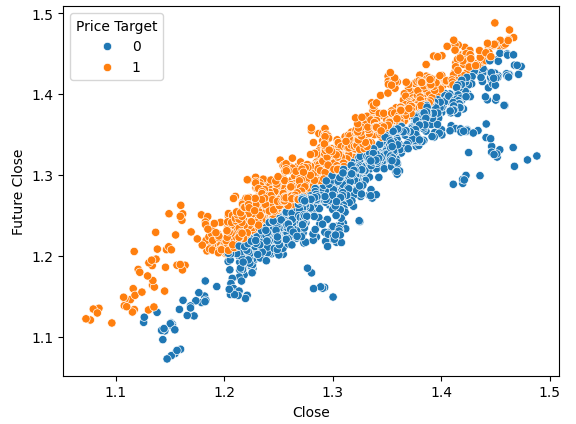
Abb. 5: Ein theoretisches Beispiel dafür, wie eine gute Trennung aussieht

Wie Sie sehen können, gibt es eine klare Trennung zwischen den beiden Klassen in diesem Diagramm. Dies ist zu erwarten, da wir das Ziel selbst in der Darstellung verwenden. Unser Ziel als Praktiker des maschinellen Lernens ist es, ein Merkmal oder Ziel zu finden, das uns einen Trennungsgrad liefert, der dem in Abb. 4 dargestellten nahe kommt.

Wenn wir dieselbe Darstellung mit unserem neuen Ziel durchführen, beobachten wir etwas Seltsames.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Future Close",hue="New Target")

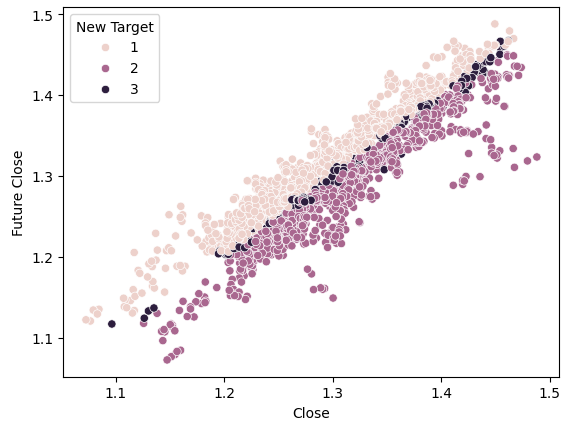
Abb. 6: Visualisierung der durch das neue Ziel bewirkten Trennung

Beachten Sie, dass die dunklen und hellen Punkte in der oberen und unteren Hälfte des Diagramms gut voneinander getrennt sind, da sie die Fälle darstellen, in denen der Preis gestiegen bzw. gefallen ist. Zwischen diesen beiden Klassen gibt es Punkte, die als Zustand 3 eingestuft werden, gekennzeichnet durch die dunklen Punkte in der Mitte, die Fälle anzeigen, in denen der Preis schwankte.

Ausbildung der Modelle

Wir werden nun die benötigten Modelle und andere Vorverarbeitungswerkzeuge importieren.

#Let's get a group of different models
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neural_network import MLPClassifier
from sklearn.svm import LinearSVC
#Import cross validation libraries
from sklearn.model_selection import TimeSeriesSplit
#Import accuracy metrics
from sklearn.metrics import accuracy_score
#Import preprocessors
from sklearn.preprocessing import RobustScaler

Wir werden die Parameter für unsere Zeitreihen-Kreuzvalidierung definieren. Denken Sie daran, dass der Abstand mindestens unserem Prognosehorizont entsprechen sollte.

#Splits
splits = 10
gap = look_ahead

Lassen Sie uns alle Modelle, die wir benötigen, in einer Liste speichern, damit wir alle Modelle, die wir haben, programmatisch anpassen können.

#Store each of the models we need
cols = ["AdaBoostClassifier","Linear DiscriminantAnalysis","Bagging Classifier","Random Forest Classifier","KNeighborsClassifier","Neural Network Small","Neural Network Large"]
models = [AdaBoostClassifier(),LinearDiscriminantAnalysis(),BaggingClassifier(n_jobs=-1),RandomForestClassifier(n_jobs=-1),KNeighborsClassifier(n_jobs=-1),MLPClassifier(hidden_layer_sizes=(5,2),early_stopping=True,max_iter=1000),MLPClassifier(hidden_layer_sizes=(20,10),early_stopping=True,max_iter=1000)]
#Create data frames to store our accuracy with different models on different targets
index = np.arange(0,splits)
price_target = pd.DataFrame(columns=cols,index=index)
new_target = pd.DataFrame(columns=cols,index=index)

Wir erstellen unser geteiltes Zeitreihenobjekt für unseren Kreuzvalidierungstest.

#Create the tscv splits
tscv = TimeSeriesSplit(n_splits=splits,gap=gap)

Lassen Sie uns die Prädiktoren und das Ziel für unsere Modelle definieren.

#Define the predictors and target
predictors = ["Open","High","Low","Close"]
target = "New Target"

Durchführung der Kreuzvalidierung.

#Now we perform cross validation
for j in (np.arange(len(models))):
    #We need to train each model
    model = models[j]
    for i,(train,test) in enumerate(tscv.split(gbpusd)):
        #Scale the data
        scaler = RobustScaler()
        X_train_scaled = scaler.fit_transform(gbpusd.loc[train[0]:train[-1],predictors])
        scaler = RobustScaler()
        X_test_scaled = scaler.fit_transform(gbpusd.loc[test[0]:test[-1],predictors])
        #Train the model
        model.fit(X_train_scaled,gbpusd.loc[train[0]:train[-1],target])
        #Measure the accuracy
        new_target.iloc[i,j] = accuracy_score(gbpusd.loc[test[0]:test[-1],target],model.predict(X_test_scaled))

Betrachten wir die Leistung jedes unserer Modelle auf dem einfachsten möglichen Ziel.

#Calculate the mean for each column when predicting price 
for i in np.arange(0,len(models)):
    print(f"{cols[i]} achieved accuracy: {price_target.iloc[:,i].mean()}")

AdaBoostClassifier erreicht Genauigkeit: 0.5190265486725664
Die lineare Diskriminanzanalyse erzielte eine hohe Genauigkeit: 0.5579646017699115
Der Bagging Classifier erreichte eine hohe Genauigkeit: 0.5075221238938052
Der Random Forest Classifier erreichte eine hohe Genauigkeit: 0.5349557522123894
KNeighborsClassifier erreichte eine Genauigkeit von: 0.536283185840708
Neural Network Small erreichte eine Genauigkeit von: 0.45309734513274336
Neuronales Netz Große erreichte eine Genauigkeit von: 0.5446902654867257

Die lineare Diskriminanzanalyse schnitt bei diesem speziellen Datensatz am besten ab und erreichte eine Genauigkeit von fast 56 %. Doch nun wollen wir sehen, wie wir mit dem neuen Ziel zurechtkommen.

#Calculate the mean for each column when predicting price 
for i in np.arange(0,len(models)):
    print(f"{cols[i]} achieved accuracy: {new_target.iloc[:,i].mean()}")

AdaBoostClassifier erreicht Genauigkeit: 0.45929203539823016
Die lineare Diskriminanzanalyse erzielte eine hohe Genauigkeit: 0.4668141592920355
Der Bagging Classifier erreichte eine hohe Genauigkeit: 0.4393805309734514
Der Random Forest Classifier erreichte eine hohe Genauigkeit: 0.45929203539823016
KNeighborsClassifier erreichte eine Genauigkeit von: 0.465929203539823
Neural Network Small erreichte eine Genauigkeit von: 0.3920353982300885
Neuronales Netz Große erreichte eine Genauigkeit von: 0.4606194690265487

In beiden Fällen stand die LDA immer noch ganz oben auf unserer Liste. Alle Modelle zeigten eine schwächere Leistung bei dem neuen Ziel, aber das kleine neuronale Netz erlitt den größten Leistungsabfall.

Modell	Veränderung der Leistung
AdaBoostClassifier	-14.32748538011695%
Die Lineare Diskriminanzanalyse.	-19.526066350710863%
Bagging Classifier	-22.09660842754366%
Random Forest Classifier	-16.730769230769248%
KNeighborsClassifier	-15.099715099715114%
Neuronales Netz Klein	-41.04193138500632%
Neuronales Netz groß	-21.1502782931354%

Analysieren wir nun die Konfusionsmatrix unseres leistungsstärksten Modells.

#Let's continue analysing the performance of our best model Linear Discriminant Analysis
from mlxtend.evaluate import confusion_matrix
from mlxtend.plotting import plot_confusion_matrix
model = LinearDiscriminantAnalysis()
model.fit(gbpusd.loc[0:1000,predictors],gbpusd.loc[0:1000,"New Target"])
cm = confusion_matrix(y_target=gbpusd.loc[1000:,"New Target"],y_predicted=model.predict(gbpusd.loc[1000:,predictors]),binary=True)
fig , ax = plot_confusion_matrix(cm)

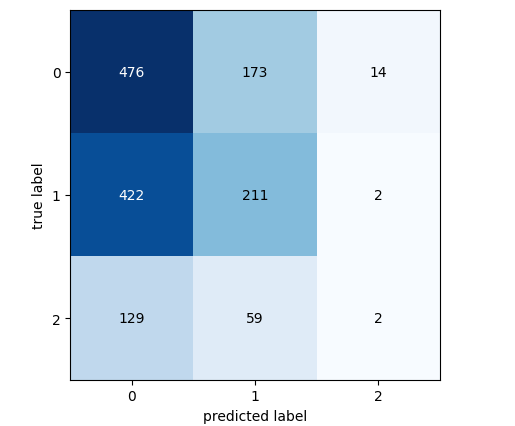
Abb. 7: Die Konfusionsmatrix für unser LDA-Modell

Anhand der Konfusionsmatrix können wir feststellen, welche Klassen für unser Modell eine Herausforderung darstellen. Wie aus der obigen Grafik hervorgeht, schnitt unser Modell bei der Vorhersage der Klasse 3 am schlechtesten ab. Allerdings gibt es in dieser Klasse nur eine kleine Anzahl von Beobachtungen. Um dieses Problem zu lösen, müssen wir möglicherweise Daten verwenden, die die gesamte Population besser repräsentieren. Wir können dies erreichen, indem wir mehr historische Daten abrufen oder niedrigere Zeitrahmen analysieren.

Auswahl der Merkmale

Manchmal können wir die Leistung verbessern, indem wir unnötige Merkmale aus unseren Modellen streichen. Konzentrieren wir uns auf unser leistungsstärkstes Modell, LDA, und ermitteln wir seine wichtigsten Merkmale, um zu sehen, ob wir die Leistung weiter verbessern können.

#Now let us perform feature selection
from mlxtend.feature_selection import SequentialFeatureSelector

Es gibt viele Algorithmen für die Merkmalsauswahl, und in diesem Artikel haben wir den Algorithmus für die Vorwärtsauswahl von Merkmalen verwendet. Es gibt zwar verschiedene Versionen dieses Algorithmus, aber der allgemeine Prozess beginnt mit einem Nullmodell, das als Benchmark dient. Der Algorithmus wertet dann jedes der p verfügbaren Merkmale einzeln aus und wählt dasjenige, das die größte Leistungsverbesserung bewirkt, als erstes Merkmal aus. Dieser Vorgang wird für die übrigen p-1 Prädiktoren wiederholt. Dank der jüngsten Fortschritte auf dem Gebiet der parallelen Datenverarbeitung sind solche Algorithmen leichter realisierbar geworden.

Wenn wir unsere Prädiktoren von p auf k reduzieren, wobei k<p ist, und die k Merkmale klug auswählen, können wir entweder unser ursprüngliches Modell übertreffen oder ein Modell erhalten, das ebenso zuverlässig, aber schneller zu trainieren ist. Außerdem kann eine Verringerung der Anzahl der im Modell verwendeten Prädiktoren die Varianz der Koeffizienten unseres Modells verringern.

Dieser Algorithmus weist jedoch 2 starke Einschränkungen auf, die es zu diskutieren gilt. Erstens könnte das neue Modell aufgrund der begrenzten Informationen, die wir zum Trainieren verwenden, etwas verzerrter sein. Darüber hinaus hat die Wahl des ersten Merkmals Einfluss auf die nachfolgenden Auswahlen. Wenn das anfänglich gewählte Merkmal nur wenig mit dem Ziel zu tun hat, können nachfolgende Merkmale aufgrund dieser anfänglichen schlechten Wahl uninformativ erscheinen.

In unserer Analyse haben wir der Eigenschaftsauswahl (Feature Selector) erlaubt, so viele Variablen auszuwählen, wie er für wichtig hält, aber er hat nur eine ausgewählt: den Eröffnungskurs.

#Forward feature selection 
forward_feature_selection = SequentialFeatureSelector(LinearDiscriminantAnalysis(),
                                                     k_features =(1,4),
                                                     forward=True,
                                                     verbose=2,
                                                     scoring="accuracy",
                                                     cv=5,
                                                     n_jobs=-1).fit(gbpusd.loc[:,predictors],gbpusd.loc[:,"New Target"])

Jetzt wollen wir die beste Eigenschaft sehen.

#Best feature
forward_feature_selection.k_feature_names_

(Open,)

Beobachten wir unsere neuen Genauigkeitsstufen.

#Update the predictors and target
predictors = ["Open"]
target = "New Target"
best_features_for_new_target = pd.DataFrame(columns=["Linear Discriminant Analysis"],index=index)

Führen wir eine Kreuzvalidierung mit dem besten Merkmal durch, das wir identifiziert haben.

#Now we perform cross validation
for i,(train,test) in enumerate(tscv.split(gbpusd)):
    #First initialize the model
    model = LogisticRegression()
    #Train the model
    model.fit(gbpusd.loc[train[0]:train[-1],predictors],gbpusd.loc[train[0]:train[-1],target])
    #Measure the accuracy
    best_features_for_new_target.iloc[i,0] = accuracy_score(gbpusd.loc[test[0]:test[-1],target],model.predict(gbpusd.loc[test[0]:test[-1],predictors]))

Schauen wir uns die neuen Genauigkeitsstufen an.

#New accuracy only using the open price
best_features_for_new_target.iloc[:,0].mean()

0.46548672566371685

Und schließlich wollen wir die Veränderung der Leistung zwischen dem Modell, das alle Prädiktoren verwendet, und dem Modell, das nur einen verwendet, betrachten.

-0.0013274336283186638

Wie wir sehen können, beträgt die Veränderung der Leistung etwa -0,2 %. Das bedeutet, dass wir durch den Verzicht auf die anderen 3 Prädiktoren nur sehr wenige Informationen verloren haben.

Umsetzung der Strategie in MQL5

Wir beginnen mit dem Import der benötigten Bibliotheken.

//+------------------------------------------------------------------+
//|                                   Forecasting Highs And Lows.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com"
#property version   "1.00"

//+------------------------------------------------------------------+
//|Libraries we need                                                 |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh> //Trade class
CTrade Trade;             //Initialize the class

Dann definieren wir Eingabevariablen, sodass der Endnutzer seine Erfahrung anpassen kann.

//+------------------------------------------------------------------+
//| Input variables                                                  |
//+------------------------------------------------------------------+
input int fetch = 10; //How much data should we fetch?
input int look_ahead = 2; //Forecst horizon.
input int rsi_period = 20; //Forecst horizon.
int input  lot_multiple = 1; //How many times bigger than minimum lot?
input double stop_loss_values = 1; //How large should our stop loss be?

Wir benötigen einige globale Variablen, die in unserer gesamten Anwendung verwendet werden.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
vector state = vector::Zeros(3);//This vector will store the state of the system using binary mapping
double minimum_volume;//The smallest contract size allowed
vector input_data;//Input data
vector output_data;//Output data
vector rsi_data;//RSI output data
double variance;//This is the variance of our input data
int classes = 3;//The total number of output classes we have
vector mean_values = vector::Zeros(classes);//This vector will store the mean value for each class
vector probability_values = vector::Zeros(classes);//This vector will store the prior probability the target will belong each class
vector total_class_count = vector::Zeros(classes);//This vector will count the number of times each class was the target
int rsi_handler;//This will store our RSI handler
int forecast = 0;//Our model's forecast
double discriminant_values[3];//The discriminant function

Dann werden wir das Initialisierungsverfahren für unseren Expert Advisor definieren. Unsere Prozedur stellt zunächst sicher, dass der Nutzer gültige Eingaben gemacht hat, und fährt dann fort, unseren technischen Indikator einzurichten und den Status unseres Handelssystems zu initialisieren.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Validate inputs
   if(!valid_inputs())
     {
      //User passed invalid inputs
      Print("Invalid inputs were received!");
      return(INIT_FAILED);
     }
//--- Load input data
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,rsi_period,PRICE_CLOSE);
//--- Market data
   minimum_volume = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
//--- Update system state
   update_system_state(0);
//--- End of initialization
   return(INIT_SUCCEEDED);
  }

Wir müssen auch ein Deinitialisierungsverfahren für unsere Anwendung definieren.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Remove indicators
   IndicatorRelease(rsi_handler);
//--- Detach the Expert Advisor
   ExpertRemove();
//--- End of deinitialization
  }

Wir werden eine Funktion entwickeln, die uns bei der Analyse hilft, ob wir Einstiegssignale haben. Unsere Einstiegssignale werden als gültig angesehen, wenn die Prognose des Modells mit dem Trend auf höheren Zeitrahmen, wie dem wöchentlichen, übereinstimmt. Wenn die beiden Werte übereinstimmen, werden wir unsere Einstiege mit Hilfe des RSI-Indikators timen.

//+------------------------------------------------------------------+
//| This function will analyse our entry signals                     |
//+------------------------------------------------------------------+
void analyse_entry(void)
  {
   Print("Higher Time Frame Trend");
   Print(iClose(_Symbol,PERIOD_W1,12) - iClose(_Symbol,PERIOD_CURRENT,0));
   if(iClose(_Symbol,PERIOD_W1,12) < iClose(_Symbol,PERIOD_CURRENT,0))
     {

      if(forecast == 1)
        {
         bullish_sentiment();
        }
     }
   if(iClose(_Symbol,PERIOD_W1,12) > iClose(_Symbol,PERIOD_CURRENT,0))
     {

      if(forecast == 2)
        {
         bearish_sentiment();
        }
     }
  }

Für die Interpretation unseres RSI-Indikators benötigen wir zwei spezielle Funktionen, von denen eine den Indikator auf Verkaufsgelegenheiten und die andere auf Kaufgelegenheiten untersucht.

//+------------------------------------------------------------------+
//| This function will analyze our RSI for sell signals              |
//+------------------------------------------------------------------+
void bearish_sentiment(void)
  {
   rsi_data.CopyIndicatorBuffer(rsi_handler,0,0,1);
   if(rsi_data[0] < 50)
     {
      Trade.Sell(minimum_volume * lot_multiple,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_BID),(SymbolInfoDouble(_Symbol,SYMBOL_BID) + stop_loss_values),(SymbolInfoDouble(_Symbol,SYMBOL_BID) - stop_loss_values));
      update_system_state(2);
     }
  }
//+------------------------------------------------------------------+
//| This function will analyze our RSI for buy signals               |
//+------------------------------------------------------------------+
void bullish_sentiment(void)
  {
   rsi_data.CopyIndicatorBuffer(rsi_handler,0,0,1);
   if(rsi_data[0] > 50)
     {
      Trade.Buy(minimum_volume * lot_multiple,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_ASK),(SymbolInfoDouble(_Symbol,SYMBOL_ASK) - stop_loss_values),(SymbolInfoDouble(_Symbol,SYMBOL_ASK) +stop_loss_values));
      update_system_state(2);
     }
  }

Wir werden nun eine Funktion definieren, die die Eingaben überprüft, die der Nutzer bei der Initialisierung eingegeben hat.

//+------------------------------------------------------------------+
//|This function will check the inputs the user passed               |
//+------------------------------------------------------------------+
bool valid_inputs(void)
  {
//--- For the inputs to be valid:
//--- The forecast horizon must be less than the data fetched
   return((fetch > look_ahead));
  }

Wir wollen nun eine Funktion entwerfen, die unser LDA-Modell initialisiert.

//+------------------------------------------------------------------+
//| This function will initialize our model                          |
//+------------------------------------------------------------------+
void initialize_model(void)
  {
//--- First fetch the input data
   fetch_input_data(look_ahead,fetch);
   fetch_output_data(0,fetch);
//--- Update the system state
   update_system_state(1);
//--- Fit the model
   fit_model();
  }

Um das Modell zu initialisieren, müssen wir zunächst die Eingabedaten für das Modell abrufen, dafür ist diese Funktion zuständig. Beachten Sie, dass die Funktion lediglich den Eröffnungskurs abruft, da unsere Analyse ergab, dass dies die wichtigste Funktion ist, die wir haben.

//+------------------------------------------------------------------+
//| This function will fetch our input data                          |
//+------------------------------------------------------------------+
void fetch_input_data(int start,int size)
  {
//--- Fetching input data
   Print("Fetching input data");
   input_data = vector::Zeros(fetch);
   input_data.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_OPEN,start,size);
   input_data.Resize(size);
   Print("Input data fetched");
  }

Dann müssen wir unsere Ausgabedaten holen und sie kennzeichnen. Beachten Sie auch, dass wir verfolgen, wie oft jede Klasse als Ziel vorkam, diese Information wird später verwendet, wenn wir das LDA-Modell anpassen.

//+------------------------------------------------------------------+
//| This function will fetch our output data                         |
//+------------------------------------------------------------------+
void fetch_output_data(int start,int size)
  {
//--- Fetching output data
   vector historic_high = vector::Zeros(size);
   vector historic_low = vector::Zeros(size);
   vector historic_close = vector::Zeros(size);
   historic_close.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,start,size+look_ahead);
   historic_low.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_HIGH,start,size+look_ahead);
   historic_high.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_LOW,start,size+look_ahead);
   output_data = vector::Zeros(size);
   output_data.Resize(size);
//--- Reset class counts
   total_class_count[0] = 0;
   total_class_count[1] = 0;
   total_class_count[2] = 0;
//--- Label the data
   for(int i = 0; i < size; i++)
     {
      //--- Price broke into a higher high
      if(historic_close[i + look_ahead] > historic_high[i])
        {
         output_data[i] = 1;
         total_class_count[0] += 1;
        }
      //--- Price broke into a lower low
      else
         if(historic_close[i + look_ahead] < historic_low[i])
           {
            output_data[i] = 2;
            total_class_count[1] += 1;
           }
         //--- Price was stuck in a range
         else
            if((historic_close[i + look_ahead] > historic_low[i]) && (historic_close[i + look_ahead] < historic_high[i]))
              {
               output_data[i] = 3;
               total_class_count[2] += 1;
              }
     }
//--- We fetched output data succesfully
   Print("Output data fetched");
   Print("Total class counts");
   Print(total_class_count);
  }

Nun definieren wir das Verfahren zur Anpassung des LDA-Modells. In einem ersten Schritt berechnen wir den Durchschnittswert des Eröffnungskurses in jeder der 3 Klassen. Der zweite Schritt erfordert die Berechnung der Wahrscheinlichkeitsverteilung, dass es sich bei jeder Klasse um die Zielklasse handelt. Wir können diesen Wert einfach anhand der im vorherigen Schritt durchgeführten Klassenzählungen schätzen. Schließlich müssen wir die Varianz des Open-Preises für jede der 3 Klassen berechnen.

//+------------------------------------------------------------------+
//| This function will fit the LDA algorithm                         |
//+------------------------------------------------------------------+
//--- Fit the model
void fit_model(void)
  {
//--- To fit the LDA model, we first need to know the mean value of X for each of our 3 classes
   double sum_class_one = 0;
   double sum_class_two = 0;
   double sum_class_three = 0;

//--- In this case we only have 1 input
   for(int i = 0; i < fetch;i++)
     {
      //--- Class 1
      if(output_data[i] == 1)
        {
         sum_class_one += input_data[i];
        }
      //--- Class 2
      else
         if(output_data[i] == 2)
           {
            sum_class_two += input_data[i];
           }
         //--- Class 3
         else
            if(output_data[i] == 3)
              {
               sum_class_three += input_data[i];
              }
     }
//--- Calculate the mean value for each class
   mean_values[0] = sum_class_one / total_class_count[0];
   mean_values[1] = sum_class_two / total_class_count[1];
   mean_values[2] = sum_class_three / total_class_count[2];
   Print("Mean values");
   Print(mean_values);
//--- Now we need to calculate class probabilities
   for(int i=0;i<classes;i++)
     {
      probability_values[i] = total_class_count[i] / fetch;
     }
   Print("Class probability values");
   Print(probability_values);
//--- Calculating the variance
   Print("Calculating the variance");
//--- Next we need to calculate the variance of the inputs within each class of y.
//--- This process can be simplified into 2 steps
//--- First we calculate the difference of each instance of x from the group mean.
   double squared_difference[3];
   for(int i =0; i < fetch;i++)
     {
      //--- If the output value was 1, find the input value that created the output
      //--- Calculate how far that value is from it's group mean and square the difference
      if(output_data[i] == 1)
        {
         squared_difference[0] = MathPow((input_data[i]-mean_values[0]),2);
        }

      else
         if(output_data[i] == 2)
           {
            squared_difference[1] = MathPow((input_data[i]-mean_values[1]),2);
           }

         else
            if(output_data[i] == 3)
              {
               squared_difference[2] = MathPow((input_data[i]-mean_values[2]),2);
              }
     }
//--- Show the squared difference values
   Print("Squared difference value for each output value of y");
   ArrayPrint(squared_difference);

//--- Next we calculate the variance as the average squared difference from the mean
   variance = (1.0/(fetch - 3.0)) * (squared_difference[0] + squared_difference[1] + squared_difference[2]);
   Print("Variance: ",variance);
  }

Jetzt brauchen wir eine Funktion, um Vorhersagen von unserem Modell abzurufen. Unser Modell wird einen Diskriminanzwert für jede der 3 möglichen Klassen vorhersagen. Die Klasse mit dem größten Diskriminanzwert ist die vorhergesagte Klasse.

//+-------------------------------------------------------------------+
//| This model will fetch our model's prediction                      |
//+-------------------------------------------------------------------+
void model_forecast(void)
  {
//--- Obtain a forecast from our model
//--- First we need to fetch the most recent input data
   fetch_input_data(0,1);
//--- We need to calculate the discriminant function for each class
//--- The predicted class is the one with the largest discriminant function
   Print("Calculating discriminant values.");
   for(int i = 0; i < classes; i++)
     {
      discriminant_values[i] = (input_data[0] * (mean_values[i]/variance) - (MathPow(mean_values[i],2)/(2*variance)) + (MathLog(probability_values[i])));
     }
//--- Show the LDA prediction
   forecast = (ArrayMaximum(discriminant_values) +1);
   Print("LDA Forecast: ",forecast);
   ArrayPrint(discriminant_values);
  }

Wir brauchen eine Funktion, die den Zustand unseres Systems aktualisiert, damit unsere OnTick-Funktion immer weiß, was als Nächstes zu tun ist.

//+-------------------------------------------------------------------+
//| This function will be used to update the state of the system      |
//+-------------------------------------------------------------------+
void update_system_state(int index)
  {
//--- Each column vector is set to 0 except column 0, the first column.
//--- If the first column is set to 1, then our model has not been trained
//--- If the second column is set to 1, then our model has been trained but we have no positions
//--- If the third column is set to 1, then we have a position we need to manage
//--- Update the system state
   state = vector::Zeros(3);
   state[index] = 1;
   Print("Updating system state");
   Print(state);
  }

Definieren wir nun die Funktion OnTick, die dafür sorgt, dass alle unsere Funktionen zum richtigen Zeitpunkt aufgerufen werden.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- The model has not been trained
   if(state.ArgMax() == 0)
     {
      Print("Training the model.");
      initialize_model();
     }
//--- The model has been trained, but we have no positions
   else
      if(state.ArgMax() == 1)
        {
         Print("Finding An Entry.");
         model_forecast();
         analyse_entry();
        }
  }
//+------------------------------------------------------------------+

Abbildung 8: Unser Expert Advisor

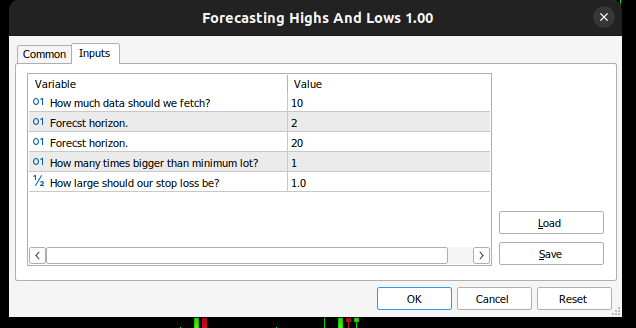
Abb. 9: Unser LDA-Expert Advisor

 

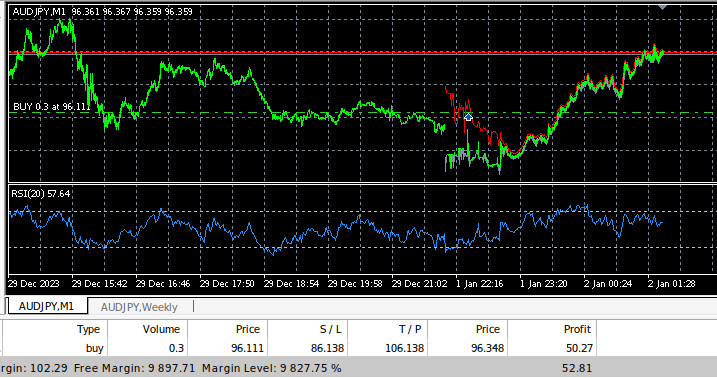
Abb. 10: Unser Expert Advisor beim Handel mit historische Daten

Schlussfolgerung

In diesem Artikel haben wir aufgezeigt, warum es für Händler besser ist, Kursänderungen zu prognostizieren als neue Höchst- und Tiefststände. Wir hoffen, dass Sie nach der Lektüre dieses Artikels mehr Vertrauen in die Entscheidung haben, ob diese Handelsstrategie für Sie geeignet ist, wenn Sie Ihre persönliche Risikotoleranz und Ihre finanziellen Ziele berücksichtigen.

Der Algorithmus der linearen Diskriminanzanalyse (LDA) modelliert die Verteilung der Eingabevariablen innerhalb jeder Klasse, wobei der Satz von Bayes zur Schätzung der Wahrscheinlichkeiten verwendet und eine Normalverteilung mit klassenspezifischen Mittelwerten und einer gemeinsamen Varianz angenommen wird. Dies hilft LDA bei der effektiven Unterscheidung von Klassenmerkmalen durch die Berechnung von Diskriminanzwerten, die die Klassentrennung maximieren und die Varianz innerhalb der Klasse minimieren. Die Annahmen von LDA können jedoch die Transparenz und Interpretierbarkeit einschränken, und es kann sein, dass einfachere Modelle ohne umfangreiche Parameterabstimmung schlechter abschneiden. Unsere Tests mit den Standardeinstellungen für tägliche Daten zeigten mögliche Leistungsprobleme auf, was darauf hindeutet, dass mit mehr Daten und Rechenressourcen bessere Ergebnisse erzielt werden könnten.

Eine Wiederholung der Analyse mit größeren Datensätzen könnte weitere Erkenntnisse liefern, allerdings ist dieser Ansatz nur mit ausreichender Rechenleistung realisierbar. Wir verwendeten eine 10-fache Zeitreihen-Kreuzvalidierung, d. h. jedes Modell wurde 10 Mal trainiert. Mit zunehmender Größe des Datensatzes könnte man erwarten, dass die Trainingszeiten für das Modell exponentiell ansteigen.