MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 13): DBSCAN für eine Klasse für Expertensignale

Einführung

Diese Artikelserie über den MQL5-Assistenten zeigt, wie oft abstrakte Ideen in der Mathematik oder in anderen Bereichen des Lebens als Handelssysteme belebt und getestet oder validiert werden können, bevor man sich ernsthaft auf sie einlässt. Diese Fähigkeit, einfache und noch nicht vollständig umgesetzte oder geplante Ideen aufzugreifen und ihr Potenzial als Handelssysteme zu erforschen, ist eines der Juwelen, die die MQL5-Assistentengruppe für Expertenberater bietet. Die Expertenklassen des Assistenten bieten viele der alltäglichen Funktionen, die von einem Expertenberater benötigt werden, insbesondere in Bezug auf das Eröffnen und Schließen von Handelsgeschäften, aber auch in übersehenen Aspekten wie der Ausführung von Entscheidungen nur bei einer neuen Balkenformation.

Indem diese Bibliothek von Prozessen als separater Aspekt eines Expertenberaters beibehalten wird, kann mit dem MQL5-Assistenten jede Idee nicht nur unabhängig getestet, sondern auch mit allen anderen Ideen (oder Methoden), die in Betracht gezogen werden könnten, auf einer einigermaßen gleichen Basis verglichen werden. In diesen Serien haben wir uns mit alternativen Clustermethoden wie dem agglomerativen Clustering und dem K-Means Clustering beschäftigt.

Bei jedem dieser Ansätze war einer der erforderlichen Eingabeparameter vor der Generierung der jeweiligen Cluster die Anzahl der zu erstellenden Cluster. Dabei wird im Wesentlichen davon ausgegangen, dass der Nutzer mit dem Datensatz gut vertraut ist und keinen unbekannten Datensatz erforscht oder betrachtet. Bei DBSCAN, Based Spatial Clustering for Applications with Noise ist die Anzahl der zu bildenden Cluster eine „respektierte“ Unbekannte. Dies bietet nicht nur mehr Flexibilität bei der Erkundung unbekannter Datensätze und der Entdeckung ihrer wichtigsten Klassifizierungsmerkmale, sondern ermöglicht auch die Überprüfung bestehender „Vorurteile“ oder allgemeiner Ansichten über einen bestimmten Datensatz daraufhin, ob die angenommene Anzahl von Clustern verifiziert werden kann.

Mit nur zwei Parametern, nämlich epsilon, dem maximalen räumlichen Abstand zwischen den Punkten in einem Cluster, und der Anzahl der Mindestpunkte, die zur Bildung eines Clusters erforderlich sind, ist DBSCAN in der Lage, aus den gesampelten Daten nicht nur Cluster zu erzeugen, sondern auch die angemessene Anzahl dieser Cluster zu bestimmen. Um seine bemerkenswerten Leistungen zu würdigen, kann es hilfreich sein, sich einige Clusterungen anzusehen, die es im Gegensatz zu alternativen Ansätzen durchführen kann.

Laut diesem Artikel würden DBSCAN und K-Means Clustering ihrer Definition nach diese unterschiedlichen Clustering-Ergebnisse liefern. 

Für K-Means Clustering würde dies ermitteln:

während DBSCAN dies ergeben würde:

Darüber hinaus hat dieser Artikel auch ein Vergleich zwischen DBSCAN und einem anderen Clustering-Ansatz namens CLARANS durchgeführt, der zu den folgenden Ergebnissen führte. Für CLARANS wurde die Neueinstufung vorgenommen:

DBSCAN mit denselben Formen ergab jedoch die folgende Gruppierung:

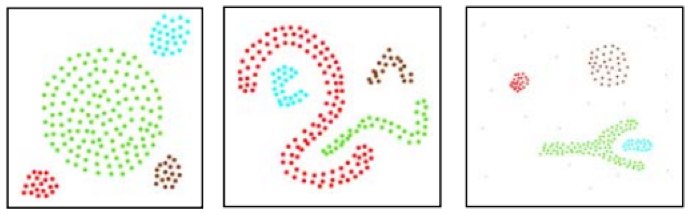
Das erste Beispiel kann eine fiktive Darstellung sein, das zweite Beispiel ist jedoch endgültig. Die Argumente dafür sind, dass DBSCAN ohne eine vorgegebene Anzahl von Clustern, die für die Klassifizierung erforderlich sind, die Dichte oder den mittleren Abstand der Punkte verwendet, um geeignete Gruppierungen und damit Cluster zu finden.

Wie aus den obigen Abbildungen ersichtlich ist, geht es bei K-Means um eine territoriale Aufteilung, die in diesem Fall durch die Koordinaten der x- und y-Achse bestimmt wird. Bei K-Means werden also die Punkte innerhalb der Achsenbeschränkungen (in diesem Fall x und y) als beste Anpassung aufgeteilt. DBSCAN führt eine zusätzliche „Dimension“ der Dichte ein, bei der es nicht ausreicht, sich nur innerhalb der Koordinatenachsen zu bewegen, sondern auch die Nähe aller Punkte zueinander berücksichtigt wird; das Ergebnis ist, dass sich Cluster über größere Regionen erstrecken können, als es ihre durchschnittliche Lage oder beste Anpassung vermuten lassen würde.

In diesem Artikel werden wir uns daher ansehen, wie DBSCAN bei der Verfeinerung von Kauf- und Verkaufsentscheidungen der im MQL5-Assistenten verwendeten Expertensignalklasse helfen kann. In den beiden oben verlinkten Artikeln zu diesen Themen haben wir bereits gesehen, wie informativ Clustering bei dieser Art von Entscheidungen sein kann. Wir werden also darauf aufbauen, wenn wir Signalklassen für DBSCAN erstellen.

Zu diesem Zweck werden wir 3 Illustrationen verschiedener Expertensignalklassen haben, die DBSCAN auf unterschiedliche Weise nutzen, vor allem bei der Verarbeitung verschiedener Datensätze. Wie bereits zu Beginn erwähnt, werden diese Ideen hier nur für vorläufige Tests und Überprüfungen vorgestellt und sind nicht annähernd das, was auf Live-Konten verwendet werden sollte. Vom Leser wird stets eigenständige Sorgfalt erwartet.

Entmystifizierung von DBSCAN

Um DBSCAN zu „entmystifizieren“, ist es vielleicht eine gute Idee, einige Illustrationen außerhalb des Handels zu geben, die uns tagtäglich begegnen werden. Schauen wir uns also 3 Beispiele an.

Beispiel 1: Stellen Sie sich eine Situation vor, in der Sie ein Supermarktbesitzer sind und einen Datensatz über einige Kunden analysieren müssen, um herauszufinden, ob es irgendwelche Muster gibt, die für zukünftige Planungszwecke genutzt werden können. Diese Analyse kann wiederum verschiedene Formen annehmen, aber für unsere Zwecke betrachten wir in erster Linie das Clustering. Bei K-Means müssen Sie zunächst von einer festen Anzahl von Kundentypen ausgehen. Nehmen wir an, Sie gehen davon aus, dass es sich bei den Kunden um solche handelt, die nur teure Konsumgüter oder elektronische Geräte kaufen, und zwar nur dann, wenn Sie ein Sonderangebot haben, und um solche, die häufig in Ihrem Geschäft anzutreffen sind und etwa einmal pro Woche Lebensmittel einkaufen. Mit dieser festgelegten Dosierung würden Sie dann fortfahren, aufzuschlüsseln, was sie kaufen, und Ihre Bestände angemessen planen, um in der Lage zu sein, ihre Nachfrage in Zukunft zu bedienen. Da Sie Ihre Cluster (Kundentypen) auf 2 voreingestellt haben, werden Sie zwangsläufig 2 größere Ausgaben haben (die zeitlich als durchschnittliche Zentren positioniert sind), um Ihren Bestand aufzufüllen, und das ist möglicherweise nicht so Cashflow-freundlich, wie Sie es gerne hätten, da mehr, aber kleinere Ausgaben besser zu bewältigen wären. Hätten Sie dagegen DBSCAN für die Segmentierung Ihrer Kunden verwendet, dann würde die Anzahl der Kundentypen, die Sie erhalten, durch ihre Dichte oder die zeitliche Nähe der Einkäufe dieser Kunden bestimmt. Wir hatten die Analogie von x- und y-Achse bei der Quantifizierung von Epsilon (Nähe von Datenpunkten) oben verwendet, aber für den Fall der Zeit mit den Supermarktkunden würde ein Kalender ausreichen, bei dem die „Nähe“ der Kunden dadurch quantifiziert wird, wie weit ihre Einkäufe zeitlich von einem Kalenderdatum entfernt sind. Dies ermöglicht eine flexiblere Gruppierung der Kunden, was wiederum zu überschaubareren Ausgaben bei der Wiederauffüllung der Bestände und anderen Vorteilen führen kann.

Beispiel 2: Stellen Sie sich eine Situation vor, in der Sie als Stadtplaner einer Stadt damit beauftragt werden, die maximale Anzahl von Wohnungen, die in jedem Bezirk der Stadt erlaubt sein sollte, auf der Grundlage einer Untersuchung der städtischen Verkehrsmuster neu zu bewerten. Während wir in Beispiel 1 die Zeit als räumliche Domäne für das Clustering verwendet haben, beschränken wir uns in diesem Beispiel auf die physischen Routen, die die Stadt durchqueren und vielleicht die Stadtteile verbinden. Bei der K-Means-Clustering-Methode würde zunächst die bestehende Anzahl der Bezirke als Cluster verwendet und dann die Gewichtung oder der Bevölkerungsschwellenwert jedes Bezirks auf der Grundlage des durchschnittlichen morgendlichen und abendlichen Verkehrsaufkommens auf seinen Verbindungsstrecken bestimmt. Mit dem neuen Gewichtungsanteil würde dann für jeden Bezirk die Wohnsitzgrenze proportional gesenkt oder erhöht werden. Die Bezirke selbst sind jedoch nicht unbedingt in Stein gemeißelt. Durch die Verwendung von DBSCAN mit nur den Verkehrsrouten und ohne Annahmen über die Anzahl der Bezirke können wir die Routen in verschiedene Formen von Clustern gruppieren, die dann unsere neuen Bezirke abbilden würden. Unser Epsilon würde in diesem Fall die Anzahl der Autos auf jeder Strecke (in den Hauptverkehrszeiten am Morgen und am Abend) auf einer Kilometerbasis erfassen. Dies könnte bedeuten, dass dichtere Strecken in Gruppen zusammengefasst werden als weniger dichte, was in Fällen, in denen Strecken in unterschiedliche geografische Gebiete führen, zu Problemen führt. Der Weg, dies zu umgehen oder die Daten zu verstehen, wäre, dass diese Strecken, auch wenn sie unterschiedlichen Gebieten zugeordnet sind, denselben „Stadtteiltyp“ repräsentieren (was auf das Einkommensniveau usw. zurückzuführen sein könnte) und daher für Planungszwecke in ähnlicher Weise bereitgestellt werden können.

Beispiel 3: Schließlich sind soziale Netzwerke für viele Unternehmen eine goldene Datenmine, und der Schlüssel zu einem besseren Verständnis dieser Netzwerke könnte in der Fähigkeit liegen, die Nutzer in verschiedene Gruppen zu klassifizieren oder in unserem Fall zu clustern. Da die Nutzer sozialer Medien in ihrer Freizeit oder bei der Arbeit eigene Gruppen bilden, gemeinsame Interessen haben oder auch nicht und sogar sporadisch interagieren, ist es für K-Means eine Herkulesaufgabe, zu Beginn des Clustering-Prozesses auf Anhieb eine akzeptable Anzahl von Clustern zu finden. DBSCAN hingegen kann durch die Konzentration auf die Dichte die Anzahl der Nutzerinteraktionen ermitteln, beispielsweise durch Aufzählung über einen bestimmten Zeitraum. Die Anzahl der Interaktionen zwischen den Nutzern kann somit als Richtschnur für den Epsilon-Parameter bei der Bildung und Definition der verschiedenen Cluster dienen, die auf einer bestimmten Social-Media-Plattform möglich sind.

Neben den Punkten, die in diesen Beispielen angesprochen wurden, ist es auch erwähnenswert, dass DBSCAN besser in der Lage ist, mit Rauschen umzugehen und Ausreißer zu identifizieren, insbesondere in Situationen des unüberwachten Lernens, wie es bei DBSCAN der Fall ist. Der Eingabeparameter Mindestpunktzahl ist ebenfalls wichtig, wenn es darum geht, die ideale Anzahl von Clustern für einen Stichprobendatensatz zu ermitteln. Er ist jedoch nicht so empfindlich (oder wichtig) wie epsilon, da seine Rolle im Wesentlichen darin besteht, den Schwellenwert für das „Rauschen“ festzulegen. Bei DBSCAN sind alle Daten, die nicht in die vorgesehenen Cluster fallen, Rauschen.

Implementierung in MQL5

Die grundlegende Struktur der aus dem MQL5-Assistenten zusammengesetzten Expertenberater wurde bereits in früheren Artikeln behandelt. Die offizielle Grundlage dazu finden Sie hier. Wie auch immer, die vom Assistenten zusammengestellten Expertenberater hängen von der Expertenklasse ab, die in der Datei „<include\Expert\Expert.mqh>“ definiert ist. Diese Expertenklasse definiert in erster Linie, wie die typischen Expertenberaterfunktionen, die sich auf das Öffnen und Schließen von Positionen beziehen, gehandhabt werden. Sie hängt wiederum von der Expert-Base-Klasse ab, die in der Datei „<include\Expert\ExpertBase.mqh>“ definiert ist, und diese Datei übernimmt das Abrufen und Zwischenspeichern aktueller Kursinformationen für das Symbol, an das der Expert Advisor gebunden ist. Von der Expert-Klasse, die wir als Anker betrachten können, werden 3 weitere Klassen durch Vererbung abgeleitet, nämlich: die Expert-Signal-Klasse, die Expert-Trailing-Klasse und die Expert-Money-Klasse. Angepasste Implementierungen jeder dieser Klassen wurden bereits in früheren Artikeln vorgestellt. Es lohnt sich jedoch, noch einmal darauf hinzuweisen, dass die Expert Signal-Klasse Kauf- und Verkaufsentscheidungen trifft, während die Expert Trailing-Klasse bestimmt, wann und um wie viel der Trailing-Stop bei offenen Positionen verschoben werden soll, und schließlich die Expert Money-Klasse festlegt, welcher Anteil der verfügbaren Margin für die Positionsgröße verwendet werden kann.

Die Schritte zur Erstellung eines Expertenberaters aus den verfügbaren Klassen in der Bibliothek sind wirklich einfach und es gibt neben dem oben genannten Link auch Artikel, die zeigen, wie man vorgeht. Die Datenaufbereitung wird von der Experten-Basisklasse übernommen. Damit diese jedoch bankfähig ist, sollten die Tests idealerweise mit den Kursdaten des gewünschten Brokers durchgeführt und echte Ticks von dessen Server heruntergeladen werden, soweit dies möglich ist.

Bei der Kodierung der DBSCAN-Funktion stellt dieser Artikel einige nützliche Quellcodes zur Verfügung, auf die wir bei der Definition unserer Funktionen aufbauen. Beginnen wir mit der einfachsten dieser Funktionen - es gibt insgesamt 4 einfache Funktionen - und betrachten wir die Abstandsfunktion.

//+------------------------------------------------------------------+
//| Function for Euclidean Distance between points                   |
//+------------------------------------------------------------------+
double CSignalDBSCAN::Distance(Spoint &A, Spoint &B)
{  double _d = 0.0;
   for(int i = 0; i < int(fmin(A.key.Size(), B.key.Size())); i++)
   {  _d += pow(A.key[i] - B.key[i], 2.0);
   }
   _d = sqrt(_d);
   return(_d);
}

Die zitierte Arbeit und der meiste öffentliche Quellcode zu DBSCAN verwenden den euklidischen Abstand als primäre Metrik zur Quantifizierung der Entfernung von Punkten in einer beliebigen Punktmenge. Da unsere Punkte jedoch in Form eines Vektors vorliegen, bietet MQL5 eine ganze Reihe anderer Alternativen zur Messung dieses Abstands zwischen Punkten, wie z. B. die Kosinusähnlichkeit usw., die der Leser erforschen kann, da sie Unterfunktionen des Datentyps Vektor sind. Wir codieren die euklidische Funktion von Grund auf neu, da ich sie nicht Teil der Verlustfunktion oder der Regressionsmetrik ist.

Als nächsten Baustein benötigen wir eine „RegionQuery“-Funktion. Diese Funktion liefert eine Liste von Punkten, die innerhalb des durch den Eingabeparameter epsilon definierten Schwellenwerts liegen und als zum selben Cluster gehörig angesehen werden können wie der betreffende Punkt.

//+------------------------------------------------------------------+
//| Function that returns neighbouring points for an input point &P[]|
//+------------------------------------------------------------------+
void CSignalDBSCAN::RegionQuery(Spoint &P[], int Index, CArrayInt &Neighbours)
{  Neighbours.Resize(0);
   int _size = ArraySize(P);
   for(int i = 0; i < _size; i++)
   {  if(i == Index)
      {  continue;
      }
      else if(Distance(P[i], P[Index]) <= m_epsilon)
      {  Neighbours.Resize(Neighbours.Total() + 1);
         Neighbours.Add(i);
      }
   }
   P[Index].visited = true;
}

Normalerweise versuchen wir, für jeden Punkt in einem betrachteten Datensatz eine solche Liste von Punkten zu erstellen, damit nichts übersehen wird, und diese Liste ist nützlich für die nächste Funktion, die Funktion „ExpandCluster“.

//+------------------------------------------------------------------+
//| Function that extends cluster for identified cluster IDs         |
//+------------------------------------------------------------------+
bool CSignalDBSCAN::ExpandCluster(Spoint &SetOfPoints[], int Index, int ClusterID)
{  CArrayInt _seeds;
   RegionQuery(SetOfPoints, Index, _seeds);
   if(_seeds.Total() < m_min_points) // no core point
   {  SetOfPoints[Index].cluster_id = -1;
      return(false);
   }
   else
   {  SetOfPoints[Index].cluster_id = ClusterID;
      for(int ii = 0; ii < _seeds.Total(); ii++)
      {  int _current_p = _seeds[ii];
         CArrayInt _result;
         RegionQuery(SetOfPoints, _current_p, _result);
         if(_result.Total() > m_min_points)
         {  for(int i = 0; i < _result.Total(); i++)
            {  int _result_p = _result[i];
               if(SetOfPoints[_result_p].cluster_id == -1)
               {  SetOfPoints[_result_p].cluster_id = ClusterID;
               }
            }
         }
      }
   }
   return(true);
}

Diese Funktion, die eine Cluster-ID und einen Punktindex annimmt, bestimmt, ob die Cluster-ID auf der Grundlage der Ergebnisse der bereits oben erwähnten Funktion zur Abfrage von Regionen neuen Punkten zugewiesen werden muss. Wenn das Ergebnis wahr ist, vergrößert sich der Cluster, andernfalls bleibt er unverändert. Im Rahmen dieser Funktion wird geprüft, ob die Punkte bereits einem Cluster zugeordnet sind, um Wiederholungen zu vermeiden, und wie oben erwähnt werden alle nicht geclusterten Punkte (die die Cluster-ID -1 behalten) als Rauschen betrachtet.

Die Zusammenführung erfolgt über die DBSCAN-Hauptfunktion, die alle Punkte eines Datensatzes durchläuft und feststellt, ob die aktuelle Cluster-ID erweitert werden muss. Die aktuelle Cluster-ID ist eine ganze Zahl, die immer dann inkrementiert wird, wenn ein neuer Cluster gebildet wird, und bei jedem Inkrement wird die Nachbarschaft aller Punkte, die zu diesem Cluster gehören, über die bereits erwähnte Funktion zur Abfrage der Region abgefragt, und diese wird über die Funktion zur Erweiterung des Clusters aufgerufen. Die Auflistung dazu finden Sie unten:

//+------------------------------------------------------------------+
//| Main clustering function                                         |
//+------------------------------------------------------------------+
void CSignalDBSCAN::DBSCAN(Spoint &SetOfPoints[])
{  int _cluster_id = -1;
   int _size = ArraySize(SetOfPoints);
   for(int i = 0; i < _size; i++)
   {  if(SetOfPoints[i].cluster_id == -1)
      {  if(ExpandCluster(SetOfPoints, i, _cluster_id))
         {  _cluster_id++;
            SetOfPoints[i].cluster_id = _cluster_id;
         }
      }
   }
}

In ähnlicher Weise wird die Struktur, die den in der obigen Auflistung als „set of points“ bezeichneten Datensatz verarbeitet, im Klassenkopf wie folgt definiert:

   struct Spoint
   {  vector            key;
      bool              visited;
      int               cluster_id;

                     Spoint()
      {              key.Resize(0);
         visited = false;
         cluster_id = -1;
      };
                    ~Spoint() {};
   };

DBSCAN als Clustering-Methode ist je nach Größe des Datensatzes mit Speicherproblemen konfrontiert. Außerdem gibt es eine Denkschule, die der Meinung ist, dass Epsilon, der wichtigste Eingabeparameter zur Messung der Clusterdichte, nicht für alle Cluster gleich sein sollte. In der Implementierung, die wir für diesen Artikel verwenden, ist dies der Fall. Es gibt jedoch Varianten von DBSCAN wie HDBSCAN, die wir in zukünftigen Artikeln behandeln werden, die nicht einmal Epsilon als Eingabe benötigen, sondern sich nur auf die Mindestanzahl von Punkten in einem Cluster verlassen, was ein weniger kritischer und empfindlicher Parameter ist, der es zu einem vielseitigeren Ansatz beim Clustering macht.

Signal-Klassen

Wenn wir auf dem aufbauen, was wir oben in der Implementierung definiert haben, können wir eine Reihe verschiedener Ansätze zum Clustern von Wertpapierkursdaten vorstellen, um Handelssignale zu generieren. Die drei zu Beginn des Artikels versprochenen Beispielansätze sind also Clustering:

- Rohdaten des OHLC-Kursbalkens,

- Änderungen der RSI-Indikatorendaten,

- und schließlich die Veränderungen des Indikators Gleitender Durchschnittspreis.

In früheren Clustering-Artikeln hatten wir ein grobes Modell, bei dem wir geclusterte Werte posthum mit eventuellen Preisänderungen gekennzeichnet haben und die aktuellen gewichteten Durchschnitte dieser Änderungen zur Erstellung unserer nächsten Prognose verwendet haben. Wir werden einen ähnlichen Ansatz wählen, aber der Hauptunterschied zwischen den beiden Methoden wird in erster Linie der Datensatz sein, der in unsere DBSCAN-Funktion eingespeist wird. Da diese Datensätze variieren, können auch die Eingabeparameter für jede Signalklasse unterschiedlich sein.

Wenn wir mit OHLC-Rohdaten beginnen, besteht unser Datensatz aus 4 Schlüsselpunkten. Der Vektor, den wir als „key“ in der Struktur „Spoint“ definiert haben, die unsere Daten enthält, wird also eine Größe von 4 haben. Diese 4 Punkte sind die jeweiligen Veränderungen der Eröffnungs-, Höchst-, Tiefst- und Schlusskurse. Wir füllen also die Struktur „Spoint“ mit den aktuellen Preisinformationen wie folgt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalDBSCAN::GetOutput()
{  double _output = 0.0;
   
...

...


   for(int i = 0; i < m_set_size; i++)
   {  for(int ii = 0; ii < m_key_size; ii++)
      {  if(ii == 0)
         {  m_model.x[i].key[ii] = (m_open.GetData(StartIndex() + i) - m_open.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 1)
         {  m_model.x[i].key[ii] = (m_high.GetData(StartIndex() + i) - m_high.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 2)
         {  m_model.x[i].key[ii] = (m_low.GetData(StartIndex() + i) - m_low.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 3)
         {  m_model.x[i].key[ii] = (m_close.GetData(StartIndex() + i) - m_close.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
      }
      if(i > 0) //assign classifier only for data points for which eventual bar range is known
      {  m_model.y[i - 1] = (m_close.GetData(StartIndex() + i - 1) - m_close.GetData(StartIndex() + i)) / m_symbol.Point();
      }
   }
   
...

   return(_output);
}

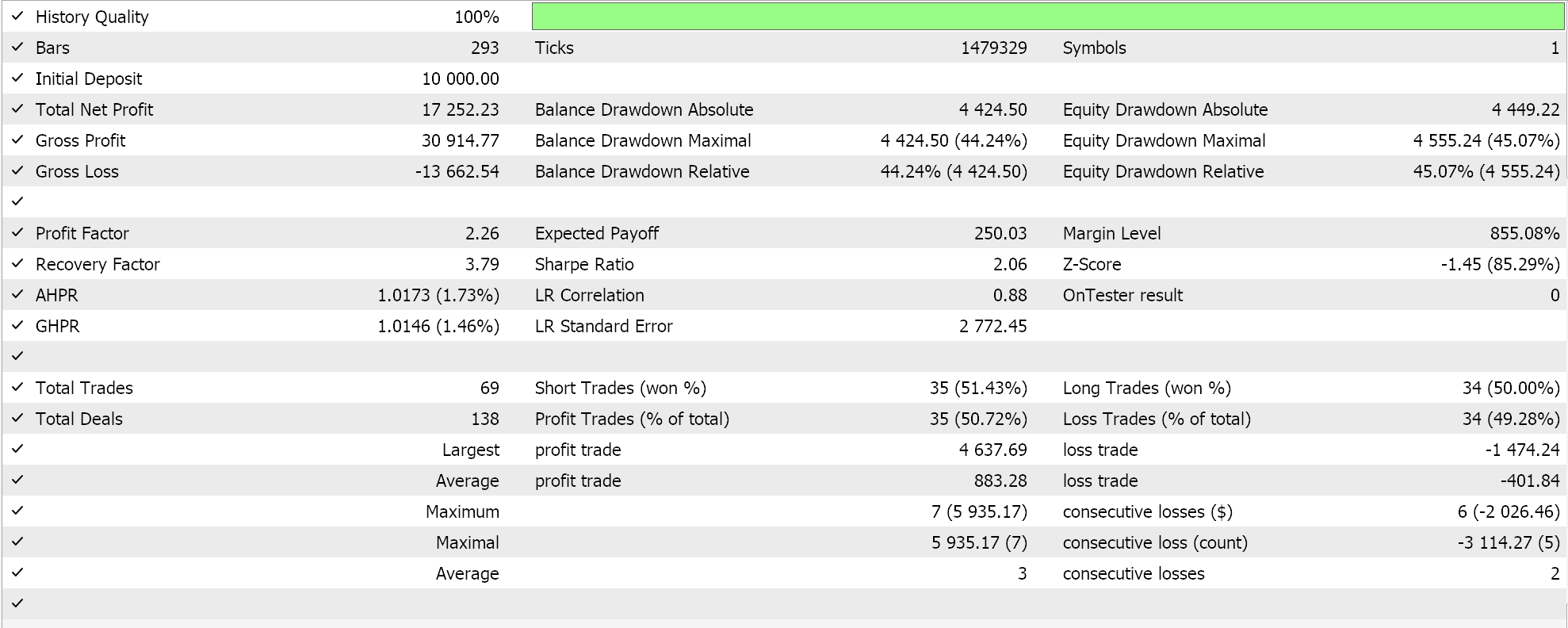
Wenn wir dieses Signal über den Assistenten zusammenstellen und Tests für EURUSD für das Jahr 2023 auf dem täglichen Zeitrahmen durchführen, ergibt unser bester Durchlauf den folgenden Bericht und die folgende Kapitalkurve.

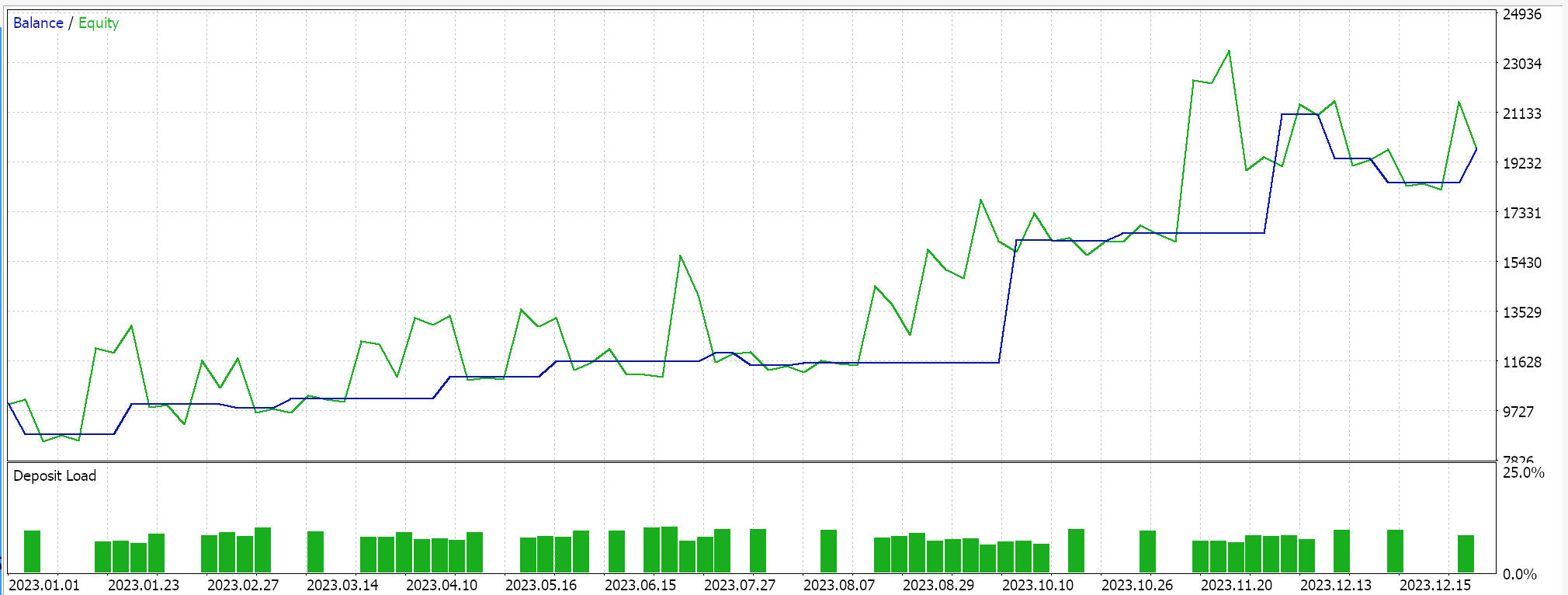
Aus den Berichten kann man schließen, dass es ein Potenzial gibt, aber in diesem Fall haben wir keinen Vorwärtstest durchgeführt, wie wir es in früheren Artikeln in kleinem Maßstab versucht hatten, sodass der Leser aufgefordert wird, dies zu tun, bevor er sich weiter damit beschäftigt.

Wenn wir mit den absoluten Werten des RSI als Datensatz fortfahren, würden wir dies in ähnlicher Weise implementieren, wobei der Hauptunterschied darin besteht, wie wir die 3 verschiedenen Verzögerungsperioden berücksichtigen, zu denen wir die RSI-Messwerte nehmen. Mit diesem Datensatz erhalten wir also 4 Datenpunkte pro Zeit wie bei den rohen OHLC-Preisen, aber diese Datenpunkte sind RSI-Indikatorwerte. Die Verzögerungen, zu denen sie genommen werden, werden durch 3 Eingabeparameter festgelegt, die wir mit A, B und C bezeichnet haben. Der Datensatz wird wie folgt gefüllt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalDBSCAN::GetOutput()
{  double _output = 0.0;

...

   RSI.Refresh(-1);
   for(int i = 0; i < m_set_size; i++)
   {  for(int ii = 0; ii < m_key_size; ii++)
      {  if(ii == 0)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i);
         }
         else if(ii == 1)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a);
         }
         else if(ii == 2)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a + m_lag_b);
         }
         else if(ii == 3)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a + m_lag_b + m_lag_c);
         }
      }
      if(i > 0) //assign classifier only for data points for which eventual bar range is known
      {  m_model.y[i - 1] = (m_close.GetData(StartIndex() + i - 1) - m_close.GetData(StartIndex() + i)) / m_symbol.Point();
      }
   }
   int _o[];

...

...

   return(_output);
}

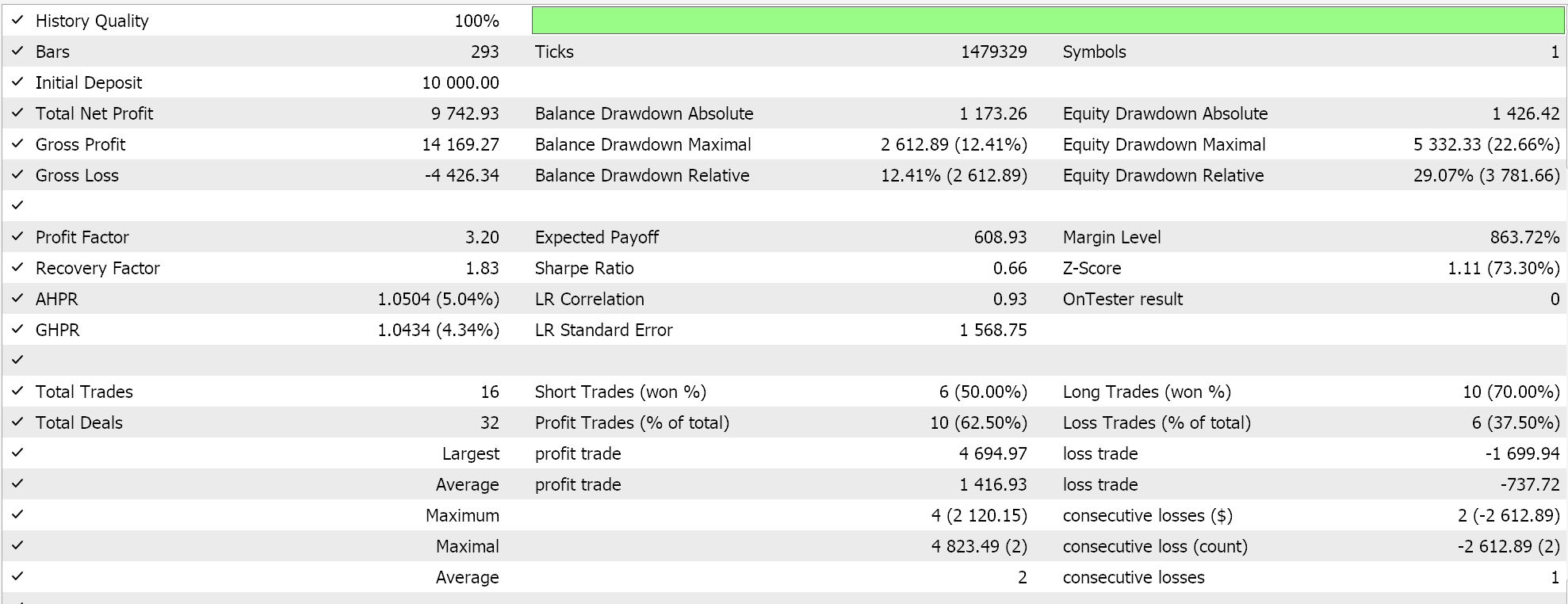
Wenn wir also Tests für das gleiche Symbol über den gleichen Zeitraum 2023 auf dem täglichen Zeitrahmen durchführen, erhalten wir die folgenden Ergebnisse aus unserem besten Lauf:

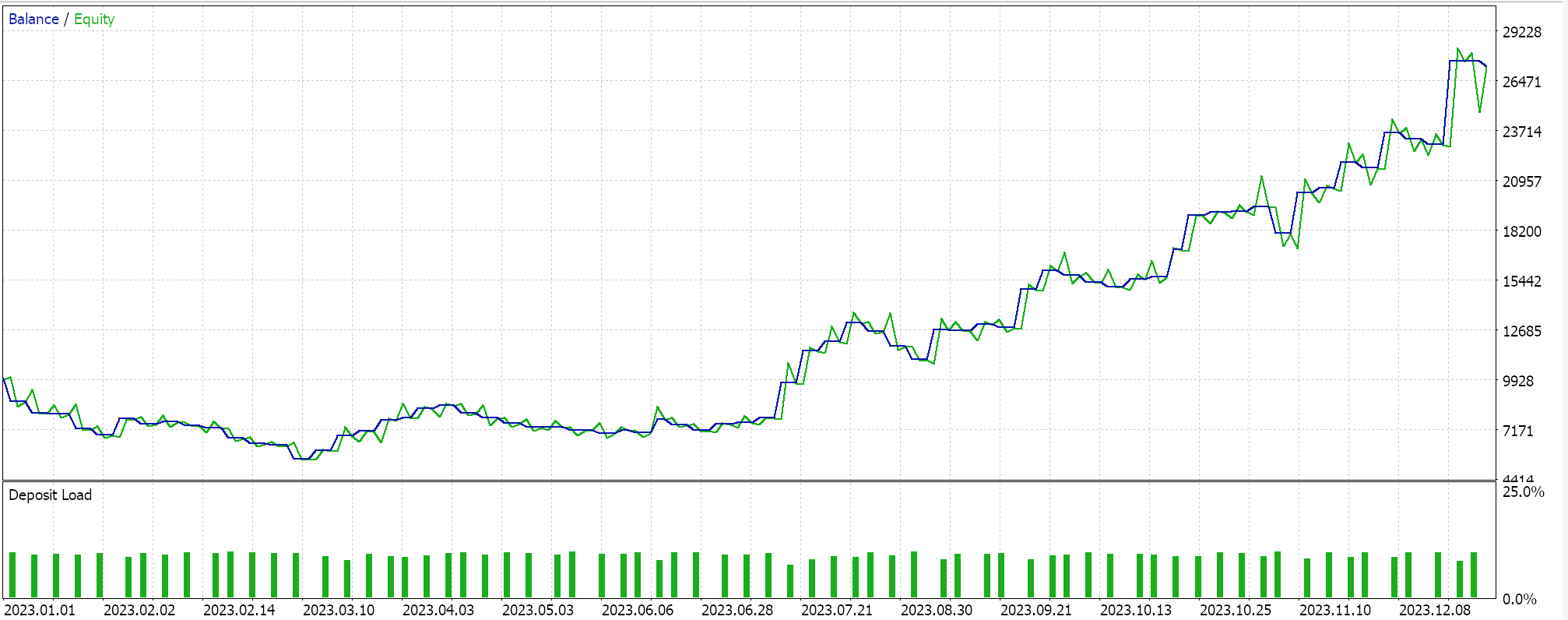
Ein vielversprechender Bericht, der aber wieder einmal nicht schlüssig ist, wenn man seine eigene Sorgfalt walten lässt. Alle für diesen Artikel zusammengestellten Experten handeln mit Limit-Orders und verwenden keine Take-Profit- oder Stop-Loss-Kurse zum Schließen von Positionen. Dies bedeutet, dass Positionen gehalten werden, bis sich ein Signal umkehrt, und dann eine neue Position in umgekehrter Richtung eröffnet wird.

Bei Veränderungen des gleitenden Durchschnitts schließlich würden wir einen Datensatz füllen, fast wie beim RSI, mit dem Hauptunterschied, dass wir hier nach Veränderungen der MA-Indikatorwerte suchen, während wir beim RSI an den absoluten Werten interessiert waren. Ein weiterer wichtiger Unterschied sind die Schlüsselwerte. Die Größe des Vektors „key“ in der Struktur „Spoint“ beträgt nur 3 und nicht 4, da wir uns auf Änderungen der Verzögerung und nicht auf absolute Messwerte konzentrieren.

Die Durchführung von Testläufen ergibt den folgenden Bericht für den besten Lauf.

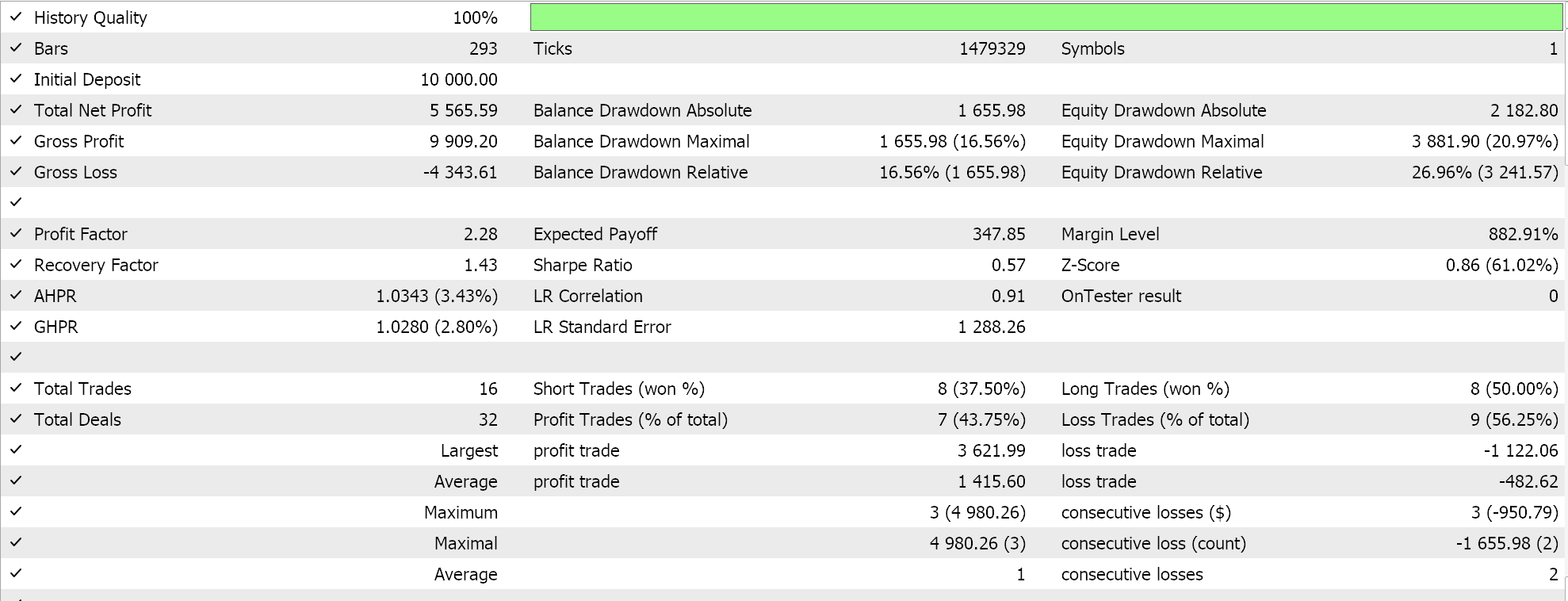
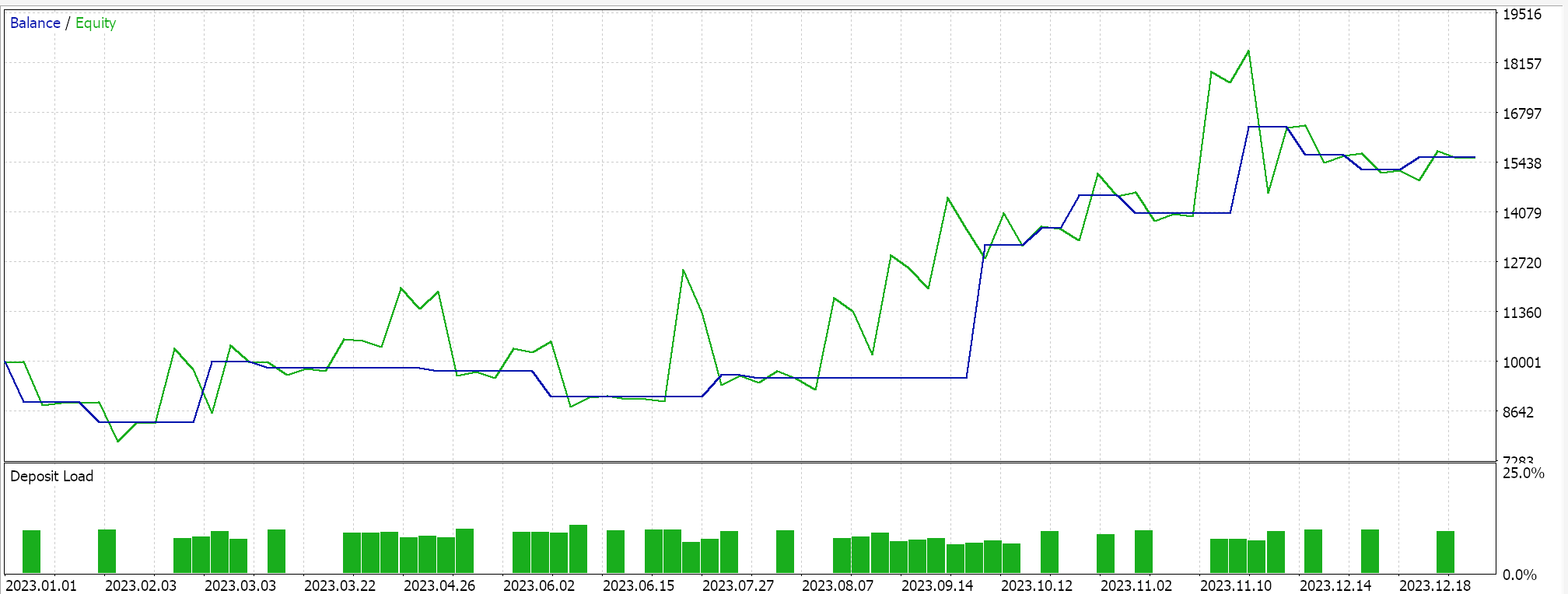
Schlussfolgerung

Zusammenfassend lässt sich sagen, dass DBSCAN eine unüberwachte Methode zur Klassifizierung von Daten ist, die im Gegensatz zu konventionellen Ansätzen wie K-Means nur minimale Eingabeparameter benötigt. Es erfordert nur zwei Parameter, von denen nur einer, epsilon, kritisch ist, was zu einer übermäßigen Abhängigkeit oder Empfindlichkeit gegenüber dieser Eingabe führt.

Trotz dieses übermäßigen Rückgriffs auf Epsilon macht die Tatsache, dass die Anzahl der Cluster für jede Klassifizierung organisch bestimmt wird, das System recht vielseitig für verschiedene Datensätze und besser in der Lage, mit Rauschen umzugehen.

Bei Verwendung innerhalb einer nutzerdefinierten Instanz der Klasse der Expertensignale kann eine Vielzahl von Eingabedatensätzen von Rohpreisen bis hin zu Indikatorwerten als Grundlage für die Klassifizierung eines Wertpapiers verwendet werden.

Neben der Erstellung einer nutzerdefinierten Instanz der Expert Signal Klasse kann der Leser ähnliche nutzerdefinierte Implementierungen der Expert Trailing Klasse oder der Expert Money Klasse erstellen, die ebenfalls DBSCAN verwenden, wie wir in früheren Artikeln dieser Serie behandelt haben.

Eine weitere Möglichkeit, die es wert ist, betrachtet zu werden, und für die DBSCAN und Clustering im Allgemeinen meiner Meinung nach prädestiniert sind, ist die Normalisierung von Daten. Viele Prognosemodelle erfordern in der Regel eine Art Normalisierung der Eingabedaten, bevor sie für die Prognose verwendet werden können. Ein Random-Forest-Algorithmus oder ein neuronales Netz benötigt beispielsweise idealerweise normalisierte Daten, insbesondere wenn es sich bei diesen Daten um Wertpapierkurse handelt. In den jetzt in Mode gekommenen großen Sprachmodellen, die die Transformer-Architektur verwenden, ist der entsprechende Schritt die Worteinbettung, bei dem im Wesentlichen der gesamte Text, einschließlich der Zahlen, für die Zwecke der Feed-Forward-Verarbeitung durch ein neuronales Netz einer Zahl neu zugewiesen wird. Ohne diese Normalisierung von Text und Zahlen wäre es für das Netzwerk unmöglich, die riesigen Datenmengen zu verarbeiten, die es für die Entwicklung von KI-Algorithmen benötigt. Aber auch diese Normalisierung befasst sich mit Ausreißern, die beim Training eines Netzwerks und bei der Festlegung akzeptabler Gewichte und Verzerrungen Kopfzerbrechen bereiten können. Es könnte noch andere sachdienliche Verwendungszwecke für Clustering und DBSCAN geben, aber das sind nur meine zwei Cents. Viel Spaß bei der Suche.