租用者 - 页 6

[Avals]

Neutron:

不，不。没有错。这里是提款金额的依赖性，它来自于迭代公式（红色），以及分析依赖性（蓝色）。

你可以看到它们是重合的，并且在k 中存在一个最大值（在主题的前一页）。

很明显，你没有离散的提款，而一定是连续的等额提款。因此，在不同时期有不同的提款方式是没有解决办法的。因此，没有办法在最后撤回所有的东西，而不在之前撤回。这不是从问题的条件得出的，而是从你应用的公式得出的（k是固定的，不是可变的ki，i=0...T）。

[Neutron]

这就对了。

[[删除]]

提取的资金总额

如果增长率足够高，效果就会变得很明显。

[Neutron]

我也有类似的依赖性。

现在我试图将导数的表达式分解为k的幂，但这并不可取--我必须持有六个数量级。很明显，这不能用分析法解决。也许还有其他想法？有人提到Diphurcs...

[[删除]]

我们需要搞清楚。

[Avals]

Neutron:

我也有类似的依赖性。

现在我试图将导数的表达式分解为k的幂，但这并不可取--我必须持有六个数量级。很明显，这不能用分析法解决。也许还有其他想法？有人提到Diphurcs...

从分析上看，这有点复杂。关于q和t。这在某种程度上取决于一种棘手的方式 :)随着q的增加，随着t的增加，最佳去除率的比例持续下降

[Alexey Subbotin]

Neutron:

我也有类似的依赖性。

现在我试图将导数的表达式分解为k的幂，但这并不可取--我必须持有六个数量级。很明显，这不能用分析法解决。也许还有其他想法？有人提到Diphurcs...

扩散法就不那么容易了--简单地改写导数中的差值是错误的，会扭曲结果，而精确的变换仍然会导致一个让人头发都竖起来的方程式，甚至更高。IMHO，不用麻烦了，在这种情况下，用数值解决问题更容易，因为函数是平滑的，有一个极值，你可以为这种快速的优化算法吃饱。

[Yury Reshetov]

你可以从特殊到一般。例如，如果t=1，你只能取钱一次，因此你必须以q的数额取钱。然后考虑t=2、t=3等的情况。

也就是说，如果在t=2时，每次提取少于q是最理想的，那么找到一个极值，并对t=2的所有q进行归纳。

类似的还有t=3，t=4等等。

从极值中，将有可能得到提款的大小为f(t)

[[删除]]

可以考虑用一个连接的船只方案来组成DU。

第一个容器的初始体积B0

[Neutron]

Reshetov:

你可以从特殊到一般。例如，如果t=1，你只能提取一次钱，因此你必须提取q的金额。然后考虑t=2、t=3等的情况。

从极值中我们将能够得到提款的大小，即f(t)

你可能是对的。除了对于 t=3，我们已经根据方程 ，在第一导数df(k)/dk=0 中的 k- 3度，我们需要寻找立方体方程的根，以及它所意味着的一切......也就是说，在这种情况下，我们不可能比t=3 更进一步。回顾一下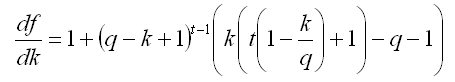， ，对于t=1的最佳尺寸k=q，对于t=2的k=q，对于t=3的k=q。但进一步增加 t， 用分析法求解是行不通的。如果你用数字求解，你可以看到，当存款增长率q 在每月10%以内时，最佳提款率在t>30 个月时变得低于q。

结论是：如果TS的可靠性使存款的平均寿命 不超过3年，那么最佳行为是每月提取所有获得的利润（存款不增长）。否则，我们需要找到一个最佳提款比例k 的分析方案，并 根据公式行事。这种情况可以保证在存款的预期寿命内获得最大的零花钱。

为了使DU，我们可以考虑连接容器的方案。第一个容器的初始体积B0

如果容器（流体流动）处于动态平衡状态（即每单位时间有多少流体流入第一个容器，就有多少流体从最后一个容器流出），那么关于每个容器中的水位问题就会得到基本解决，而不会被简化为存款问题。如果考虑到容器在其填充过程中，与存款的类比并不清楚。avtomat ，请解释一下 ，你提出这样的解释是什么意思？

P.S. 获得方程df/dk=0的近似分析解的呼吁仍然有效。欢迎提出任何意见。