租用者 - 页 2 123456789...31 新评论 Alexey Subbotin 2011.02.21 09:22 #11 Reshetov: 很明显,你应该提取q,而且只在t期结束时提取。在所有其他情况下,提取的金额将少于 刺猬决定使用分析计算))))。 Yury Reshetov 2011.02.21 09:34 #12 alsu: 这只刺猬决定使用分析计算)))) 这个问题没有极值,因为我们有一个单调增长的数字序列--一个以存款规模为参数的函数。也就是说,没有什么可以优化。参数和t越大,函数的值就越大。在任何其他情况下,该函数的值都会减少。 在一个黑暗的房间里很难找到一只黑猫,特别是如果它不在那里的话(c)孔子 Alexey Subbotin 2011.02.21 09:35 #13 Neutron: 剩下的就是取时间导数并将其等同于零......是的。 顺便说一下,如果有的话,导数应该取在k上 Neutron 2011.02.21 09:47 #14 alsu: 顺便说一下,如果有的话,导数应该取于k 对不起!真的在K 。 雷舍托夫。 很明显,你必须提取q,而且只在t期结束时提取。在所有其他情况下,提取的金额将更少。 尤拉,你是如此自信,以至于当你错了的时候都很好笑。 在第一页, avtomat 给出了一张图片,你可以清楚地看到参数k的最佳状态。 也许你只是没有注意到。我再给你看一个。 你看到最大限度了吗?不是吗?但它就在那里! 休息一下吧,你这个刺猬。 [删除] 2011.02.21 09:49 #15 Neutron: 不可能!... 你能说得更具体些吗?我的意思是,以一个公式的形式。 换句话说,在提款比例方面的最佳状态确实是可见的! 我最近解决了一个类似的问题... 然后我们把所有这些结合起来,得到两个变量的结果函数。 还应提及的是,结果取决于优化期,即 12个月的最佳值不等于3个月的四个最佳值。 Neutron 2011.02.21 10:08 #16 avtomat:我最近解决了一个类似的问题... 这就对了,avtomat。这正是它的行为方式。但我真的需要得到一个关于k 的最佳分量 的分析方案。如果你从f(k)中取k 的导数,你会得到以下的方程式。下图清楚地表明,df/dk为零的标点与f(k)的最大值相吻合。但如何解决与 k 有关的问题?Mathemat: 无论如何,这个问题与交易无关。这是一个关于租界的问题。它将相当适合该分支。 关于什么?你有没有想过,你需要多少百分比的存款才能尽可能多地提取而不耗尽它?因此,如果有人获得稳定的外汇百分比,就应该决定最佳提款百分比。 。 P.S. 我想知道, 在 这种情况 下,朱拉会 怎么做?他是不是要假装什么都没注意到(参数k 没有最大值),不对这个问题留下任何评论,或者他要重新考虑他的基本假设,为生活... Yury Reshetov 2011.02.21 10:29 #17 Neutron: P.S. 我想知道 朱拉在 这种情况 下会 怎么做?他是否会假装什么都没注意到(参数k 没有最大值),不再对这个问题留下评论,或者他将不得不修改他的主要设定点,为生活服务...... 我们仍然需要考虑这项任务,以后就会清楚了。 Neutron 2011.02.21 10:30 #18 无论如何,这是一个体面的答案。 Alexandr Andreev 2011.02.21 10:32 #19 我已被允许使用X0卢布的存款,时间为T个月。每个月的存款被记入当前存款额X的固定百分比q。我被允许每月从账户中提取一定比例的k,但不超过q的值。 我被允许以HO手数进行交易。每笔未平仓的正向交易都有u%的机会积累w点,同时从XO存款的当前价值中赚取q。我被允许以一定的百分比k部分平仓,次数不限(最高100%平仓),频率为n个点,不超过w。 问题:找到相对于u%的k、n的最佳值。 [删除] 2011.02.21 10:36 #20 Neutron: 这就对了,avtomat。这正是它的行为方式。但我真的需要得到一个关于最佳去除率k 的分析方案。如果你从f(k)中取k 的导数,你会得到以下的方程式。 下图清楚地表明,df/dk为零的标点与f(k)的最大值相吻合。 但如何解决与 k 有关的问题? 如果上述方程是真的,那么我们就可以这样做。 但还是那句话,有什么要求,有什么条件......。 q和t -- 给定的常量或... 123456789...31 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
很明显,你应该提取q,而且只在t期结束时提取。在所有其他情况下,提取的金额将少于
这只刺猬决定使用分析计算))))
这个问题没有极值,因为我们有一个单调增长的数字序列--一个以存款规模为参数的函数。也就是说,没有什么可以优化。参数和t越大,函数的值就越大。在任何其他情况下,该函数的值都会减少。
在一个黑暗的房间里很难找到一只黑猫,特别是如果它不在那里的话(c)孔子
剩下的就是取时间导数并将其等同于零......是的。
顺便说一下,如果有的话,导数应该取于k
对不起!真的在K 。
雷舍托夫。
很明显,你必须提取q,而且只在t期结束时提取。在所有其他情况下,提取的金额将更少。
尤拉,你是如此自信,以至于当你错了的时候都很好笑。
在第一页, avtomat 给出了一张图片,你可以清楚地看到参数k的最佳状态。 也许你只是没有注意到。我再给你看一个。
你看到最大限度了吗?不是吗?但它就在那里!
休息一下吧,你这个刺猬。
不可能!...
你能说得更具体些吗?我的意思是,以一个公式的形式。
换句话说,在提款比例方面的最佳状态确实是可见的!
我最近解决了一个类似的问题...
然后我们把所有这些结合起来,得到两个变量的结果函数。
还应提及的是,结果取决于优化期,即
12个月的最佳值不等于3个月的四个最佳值。
我最近解决了一个类似的问题...
这就对了,avtomat。这正是它的行为方式。但我真的需要得到一个关于k 的最佳分量 的分析方案。如果你从f(k)中取k 的导数,你会得到以下的方程式。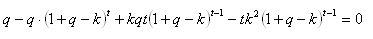
下图清楚地表明,df/dk为零的标点与f(k)的最大值相吻合。
但如何解决与 k 有关的问题?
无论如何,这个问题与交易无关。这是一个关于租界的问题。它将相当适合该分支。
。
P.S. 我想知道, 在 这种情况 下,朱拉会 怎么做?他是不是要假装什么都没注意到(参数k 没有最大值),不对这个问题留下任何评论,或者他要重新考虑他的基本假设,为生活...
P.S. 我想知道 朱拉在 这种情况 下会 怎么做?他是否会假装什么都没注意到(参数k 没有最大值),不再对这个问题留下评论,或者他将不得不修改他的主要设定点,为生活服务......
我已被允许使用X0卢布的存款,时间为T个月。每个月的存款被记入当前存款额X的固定百分比q。我被允许每月从账户中提取一定比例的k,但不超过q的值。
我被允许以HO手数进行交易。每笔未平仓的正向交易都有u%的机会积累w点,同时从XO存款的当前价值中赚取q。我被允许以一定的百分比k部分平仓,次数不限(最高100%平仓),频率为n个点,不超过w。
问题:找到相对于u%的k、n的最佳值。
这就对了,avtomat。这正是它的行为方式。但我真的需要得到一个关于最佳去除率k 的分析方案。如果你从f(k)中取k 的导数,你会得到以下的方程式。
下图清楚地表明,df/dk为零的标点与f(k)的最大值相吻合。
但如何解决与 k 有关的问题?
如果上述方程是真的,那么我们就可以这样做。
但还是那句话,有什么要求,有什么条件......。
q和t -- 给定的常量或...