交易中的混沌理论（第二部分）：深入探索

上一篇文章的摘要

第一篇文章探讨了混沌理论的基本概念及其在金融市场分析中的应用。我们研究了吸引子、分形和蝴蝶效应等关键概念，并讨论了它们如何在市场动态中显现出来。特别关注了金融背景下混沌系统的特征和波动性的概念。

我们还将经典混沌理论与比尔·威廉姆斯的方法进行了比较，这使我们能够更好地理解这些概念在交易中的科学应用和实际应用之间的差异。李雅普诺夫指数作为分析金融时间序列的工具，在该文章中占据了中心地位。我们考虑了它的理论意义和 MQL5 语言中计算的实际实现。

那篇文章的最后一部分致力于使用李雅普诺夫指数对趋势逆转和延续进行统计分析。以 H1 时段的 EURUSD 货币对为例，我们展示了如何在实践中应用这一分析，并讨论了对所得结果的解释。

该文章为在金融市场背景下理解混沌理论奠定了基础，并提出了将其应用于交易的实用工具。在第二篇文章中，我们将继续加深对这一主题的理解，重点关注更复杂的方面及其实际应用。

我们首先要讨论的是分形维数作为衡量市场混乱程度的标准。

分形维数作为市场混乱程度的衡量标准

分形维数是一个在混沌理论和包括金融市场在内的复杂系统分析中起着重要作用的概念。它提供了一种对对象或过程的复杂性和自相似性的定量衡量，使其在评估市场波动的随机程度方面特别有用。

在金融市场背景下，分形维数可用于衡量价格图的“锯齿性”。较高的分形维数表示价格结构更复杂、更混乱，而较低的分形维数可能表示更平稳、更可预测的走势。

计算分形维数的方法有几种，其中最受欢迎的方法之一是盒计数法。这种方法涉及用不同大小的单元格网格覆盖图表，并计算在不同比例下覆盖图表所需的单元格数量。

使用该方法计算分形维数 D 的公式如下：

D = -lim(ε→0) [log N(ε) / log(ε)]

其中 N(ε) 是覆盖物体所需的大小为 ε 的单元格数量。

将分形维数应用于金融市场分析可以为交易者和分析师提供对市场走势性质的额外洞察。例如：

• 识别市场模式：分形维数的变化可以指示不同市场状态之间的转变，例如趋势、平盘走势或混乱时期。
• 波动性评估：高分形维数通常对应于波动性增加的时期。
• 预测：分析分形维数随时间的变化有助于预测未来的市场走势。
• 优化交易策略：了解市场的分形结构有助于开发和优化交易算法。

现在让我们看看 MQL5 语言中计算分形维数的实际实现。我们将开发一个指标，在 MQL5 中实时计算价格图的分形维数。

该指标使用盒计数法来估计分形维数。

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

该指标使用盒子计数法计算价格图的分形维数。分形维数是衡量图表“锯齿性”或复杂性的指标，可用于评估市场的混乱程度。

输入：

• InpBoxSizesCount - 用于计算的不同“盒子”尺寸的数量
• InpMinBoxSize - 最小“盒子”尺寸
• InpMinBoxSize - 最大“盒子”尺寸
• InpDataLength - 用于计算指标的烛形数量。

指标运行算法：

1. 对于图表上的每个点，指标使用最后 InpDataLength 个烛形的数据计算分形维数。
2. 盒子计数法采用从 InpMinBoxSize 到 InpMaxBoxSize 的不同“盒子”大小。
3. 针对每个“盒子”大小计算覆盖图表所需的“盒子”数量。
4. 创建了“盒子”数量的对数与“盒子”大小的对数的依赖关系图。
5. 图形的斜率采用线性回归方法计算，是分形维数的估计值。

分形维数的变化可能预示着市场模式的改变。

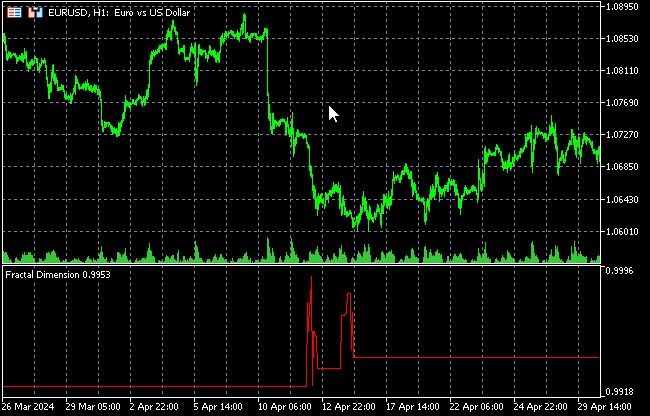
递归分析，揭示价格变动中隐藏的模式

递归分析是一种强大的非线性时间序列分析方法，可以有效地应用于研究金融市场的动态。这种方法使我们能够可视化和量化复杂动态系统中的重复模式，其中当然包括金融市场。

递归分析的主要工具是递归图。此图是系统随时间重复状态的直观表示。在递归图中，如果时间 i 和 j 的状态在某种意义上相似，则点（i，j）会被着色。

要构建金融时间序列的递归图，请按照以下步骤操作：

1. 相空间重构：使用延迟方法，我们将一维价格时间序列转换为多维相空间。
2. 确定相似度阈值：我们选择一个标准，根据这个标准，我们将认为两个状态是相似的。
3. 递归矩阵的构造：对于每对时间点，我们确定相应的状态是否相似。
4. 可视化：我们将递归矩阵显示为二维图像，其中相似的状态由点表示。

递归图使我们能够识别系统中不同类型的动态：

• 均匀区域表示平稳期。
• 对角线表示确定性动态。
• 垂直和水平结构可以表示层流条件。
• 结构的缺失是随机过程的特征。

为了量化递归图中的结构，使用了各种递归度量，如递归百分比、对角线熵、对角线的最大长度等。

将递归分析应用于金融时间序列可以帮助：

1. 识别不同的市场模式（趋势、平盘、混乱状态）
2. 检测模式的变化
3. 评估不同时期市场的可预测性
4. 揭示隐藏的周期性模式

为了在交易中实际实现递归分析，我们可以用 MQL5 语言开发一个指标，该指标将构建递归图并实时计算递归度量。这样的指标可以作为做出交易决策的附加工具，尤其是与其他技术分析方法相结合的时候。

在下一节中，我们将研究此类指标的具体实现，并讨论如何在交易策略的背景下解释其读数。

MQL5 中的递归分析指标

本指标采用了递归分析方法来研究金融市场的动态。它计算递归的三个关键指标：递归水平、确定性和分层性。

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

指标的主要特点：

指标显示在价格图表下方的独立窗口中，并使用三个缓冲区来存储和显示数据。该指标计算三个数值：递归率（蓝线），显示整体递归水平，决定性（红线），衡量系统可预测性，以及分层性（绿线），评估系统保持在特定状态的趋势。

指标输入参数包括 InpEmbeddingDimension（默认值为3），定义相空间重构的嵌入维度，InpTimeDelay（默认值为1），InpThreshold（默认值为10），以点为单位的状态相似度阈值，以及 InpWindowSize（默认值为200），用于设置分析窗口的大小。

指标运行算法基于延迟方法，用于从一维价格时间序列重建相空间。对于分析窗口中的每个点，都会计算其相对于其他点的“递归”。然后，基于获得的循环结构，计算三个衡量指标：递归率，确定递归点在总点数中的比例，确定性，显示形成对角线的递归点的比例，分层性，估计形成垂直线的递归点的比例。

Takens 嵌入定理在波动率预测中的应用

Takens 嵌入定理是动力系统理论中的一个基本结果，对包括金融数据在内的时间序列分析具有重要意义。该定理指出，可以使用时滞方法从一个变量的观测值重建动态系统。

在金融市场中，Takens 定理使我们能够从一维价格或回报时间序列重建多维相空间。这在分析波动性时特别有用，波动性是金融市场的一个关键特征。

应用 Takens 定理预测波动率的基本步骤是：

1. 相空间重构：
   • 选择嵌入维度（m）
   • 选择时间延迟 (τ)
   • 根据原始时间序列创建 m 维向量
2. 重构空间分析：
   • 寻找每个点的最近邻居
   • 局部点密度估算
3. 波动率预测：
   • 利用局部密度信息估算未来波动性

让我们更详细地看看这些步骤。

相空间重构：

假设我们有一个收盘价的时间序列 {p(t)}。我们创建 m 维向量如下：

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

其中 m 是嵌入维数，τ 是时间延迟。

选择正确的 m 和 τ 值对于成功重建至关重要。通常，使用互信息或自相关函数方法选择 τ，使用假最近邻方法选择 m。

重构空间分析：

重构相空间后，可以分析系统吸引子的结构。对于波动性预测，有关相空间中点的局部密度的信息尤为重要。

对于每个点 x(t)，我们要找到它的 k 个最近邻居（通常 k 取值范围为 5 到 20），并计算与这些邻居的平均距离。该距离是局部密度的度量，因此也是局部波动性的度量。

波动率预测

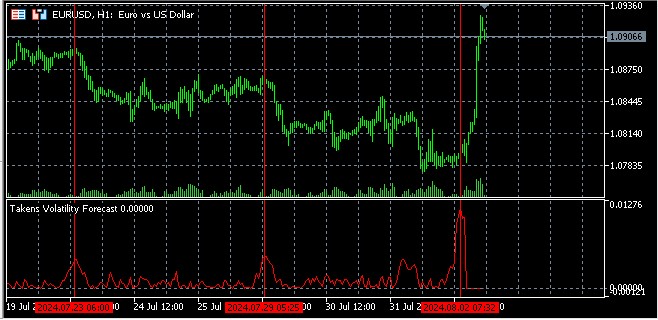
使用重构相空间预测波动率的基本思想是，在这个空间中靠近的点在不久的将来可能会有类似的行为。

为了预测 t+h 时间点的波动性，我们：

• 在重构空间中寻找当前 x(t) 点的 k 个最近邻居
• 提前 h 步计算这些邻居的实际波动率
• 使用这些波动率的平均值作为预测

在数学上，可以按如下表示：

σ̂(t+h) = (1/k) Σ σ(ti+h)，其中 ti 是 x(t) 的 k 个最近邻的索引

这种方法的优点：

• 它考虑了非线性的市场动态
• 它不需要对回报分配做出假设
• 我们能够发现波动的复杂模式

缺点：

• 它对参数（m、τ、k）的选择很敏感
• 对于大量数据来说，计算成本可能很高

实现

让我们创建一个 MQL5 指标来实现这种波动率预测方法：

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

确定时间延迟和嵌入维度的方法

利用 Takens 定理重构相空间时，正确选择两个关键参数至关重要：时间延迟 (τ) 和嵌入维数 (m)。不正确地选择这些参数可能会导致不正确的重建，从而得出错误的结论。让我们考虑两种确定这些参数的主要方法。

自相关函数 (ACF，Autocorrelation function) 方法确定时间延迟

该方法基于选择一个时间延迟 τ 的思想，自相关函数在该时间延迟 τ 处首次过零或达到某个低值，例如初始值的 1/e。这允许人们选择一个延迟，在该延迟下，时间序列的连续值变得足够相互独立。

MQL5 中 ACF 方法的实现可能如下所示：

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

在这个实现中，我们首先计算时间序列的均值和方差。然后，对于从 1 到 maxLag 的每个滞后，我们计算自相关函数的值。一旦 ACF 值小于或等于给定的阈值（默认值为 0.1），我们就会将此滞后返回为最佳时间延迟。

ACF方法有其优缺点。一方面，它易于实现并且直观。另一方面，它没有考虑数据中的非线性依赖性，这在分析通常表现出非线性行为的金融时间序列时可能是一个重大的缺点。

确定时间延迟的互信息 (MI，Mutual information) 方法

该方法基于信息论，能够考虑数据中的非线性依赖关系。这个想法是选择一个对应于互信息函数的第一个局部最小值的延迟 τ。

MQL5 中互信息方法的实现可能如下：

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

在此实现中，我们首先定义 CalculateMutualInformation 函数，该函数计算给定滞后下原始序列与其偏移版本之间的互信息。然后，在 FindOptimalLagMI 函数中，我们通过迭代不同的滞后值来搜索互信息的第一个局部最小值。

互信息方法比 ACF 方法的优势在于它能够考虑数据中的非线性依赖性。这使得它更适合分析经常表现出复杂非线性行为的金融时间序列。然而，这种方法实现起来更复杂，需要更多的计算。

ACF 和 MI 方法之间的选择取决于具体任务和所分析数据的特征。在某些情况下，使用这两种方法并比较结果可能是有用的。同样重要的是要记住，最佳时滞可能会随着时间的推移而变化，特别是对于金融时间序列，因此建议定期重新计算此参数。

确定最优嵌入维数的伪最近邻算法

一旦确定了最佳时间延迟，相空间重建的下一个重要步骤就是选择合适的嵌入维数。用于此目的的最流行的方法之一是伪最近邻（FNN，False Nearest Neighbors）算法。

FNN 算法的思想是找到一个最小嵌入维数，以正确再现相空间中吸引子的几何结构。该算法基于这样的假设，即在正确重建的相空间中，当移动到更高维的空间时，闭合点应该保持闭合。

让我们来看看 MQL5 语言中 FNN 算法的实现：

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

IsFalseNeighbor 函数确定两个点是否是假邻居。它计算当前维度中的点与大于一的维度中的点之间的距离。如果距离的相对变化超过给定的阈值，则这些点被视为假邻居。

主函数 FindOptimalEmbeddingDimension 遍历从 1 到 maxDim 的维度。对于每个维度，我们都会遍历时间序列的所有点。对于每个点，我们找到当前维度中的最近邻。然后，我们使用 IsFalseNighbor 函数检查找到的邻居是否为false。统计邻居的总数和假邻居的数量。此后，计算假邻居的比例。如果错误邻居的比例小于指定的容差阈值，则认为当前维度是最优的并返回它。

该算法有几个重要参数。delay — 先前由 ACF 或 MI 方法确定的时间延迟。maxDim — 要考虑的最大嵌入维度。threshold — 检测假邻居的阈值。tolerance — 假邻居比例的容忍阈值。这些参数的选择会显著影响结果，因此使用不同的值进行实验并考虑所分析数据的具体情况非常重要。

FNN 算法具有许多优点。它考虑了相空间中数据的几何结构。该方法对数据中的噪声具有很强的鲁棒性。它不需要对所研究系统的性质做出任何预先假设。

在 MQL5 中实现基于混沌理论的预测方法

一旦我们确定了重建相空间的最佳参数，我们就可以开始实现基于混沌理论的预测方法。该方法基于相空间中附近状态在不久的将来会有类似演化的想法。

该方法的基本思想如下：我们找到系统过去最接近当前状态的状态。根据它们未来的行为，我们对当前状态做出预测。这种方法被称为模拟或最近邻方法。

让我们看一下此方法作为 MetaTrader 5 指标的实现。指标将执行以下步骤：

1. 使用时间延迟法进行相空间重建。
2. 查找系统当前状态的 k 个最近邻。
3. 根据发现的邻居的行为预测未来的值。

以下是实现此方法的指标的代码：

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

该指标重建相空间，找到当前状态的最近邻居并使用它们的未来值进行预测。它在图表上显示实际值和预测值，使我们能够直观地评估预测的质量。

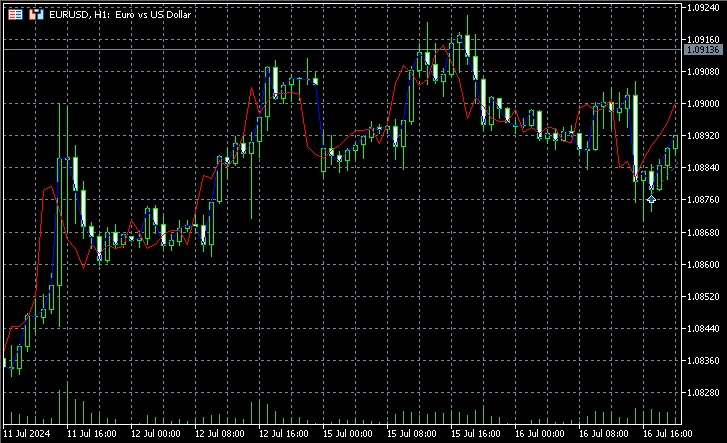
实现的关键方面包括使用加权平均值进行预测，其中每个邻居的权重与其与当前状态的距离成反比。这使我们能够考虑到，近邻可能会给出更准确的预测。从截图来看，该指标提前几个柱预测了价格走势的方向。

创建概念 EA

我们已经到达了最有趣的部分，以下是基于混沌理论的全自动工作代码：

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

此代码是 MetaTrader 5 的 EA，它使用混沌理论概念来预测金融市场的价格。EA 在重构的相空间中实现了基于最近邻方法的预测方法。

EA 具有以下输入参数：

• InPEmbeddingdiment - 用于相空间重建的嵌入维度（默认值 ：3）
• InpTimeDelay - 重建的时间延迟（默认值 ：5）
• InpNeighbors - 用于预测的最近邻居的数量（默认值 ：10）
• InpForecastHorizon - 预测范围（默认值 ：10）
• InpLookback - 分析的回顾期（默认值 ：1000）
• InpLotSize - 交易手数（默认值 ：0.1）

EA 的工作原理如下：

1. 在每个新柱上，它分别使用自相关函数 (ACF) 方法和伪最近邻 (FNN) 算法优化 optimalTimeDelay 和 optimalEmbeddingDimension 参数。
2. 然后，它使用最近邻方法根据系统的当前状态进行价格预测。
3. 如果价格预测高于当前价格，EA 将关闭所有未平仓的卖出仓位并开启一个新的买入仓位。如果价格预测低于当前价格，EA 将关闭所有未平仓的买入仓位并开启一个新的卖出仓位。

EA 使用 PredictPrice 函数，该函数：

• 使用最优嵌入维数和时间延迟重建相空间。
• 查找系统当前状态与回溯期内所有状态之间的距离。
• 按距离递增对状态进行排序。
• 计算 InpNeighbors 最近邻居的未来价格的加权平均值，其中每个邻居的权重与其与当前状态的距离成反比。
• 返回加权平均值作为价格预测。

EA 还包含 FindOptimalLagACF 和 FindOptimalEmbeddingDimension 函数，分别用于优化 optimalTimeDelay 和 optimalEmbeddingDimension 参数。

总体而言，EA 利用混沌理论的概念，为预测金融市场价格提供了一种创新方法。它可以帮助交易者做出更明智的决策，并可能提高投资回报。

使用自动优化进行测试

让我们研究一下我们的 EA 在多个交易品种上的工作。第一个货币对，EURUSD，从 2016 年 1 月 1 日起：

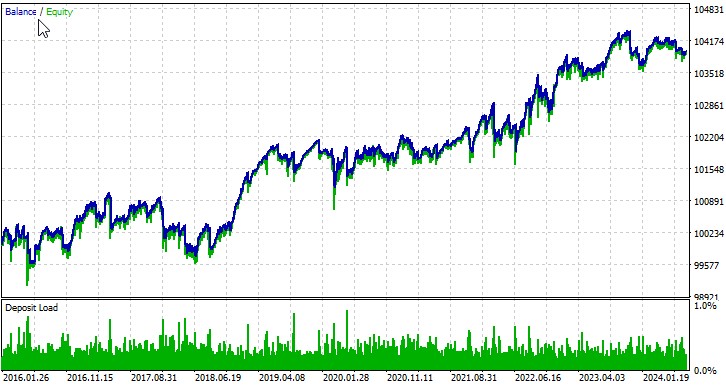
第二个货币对，AUD：

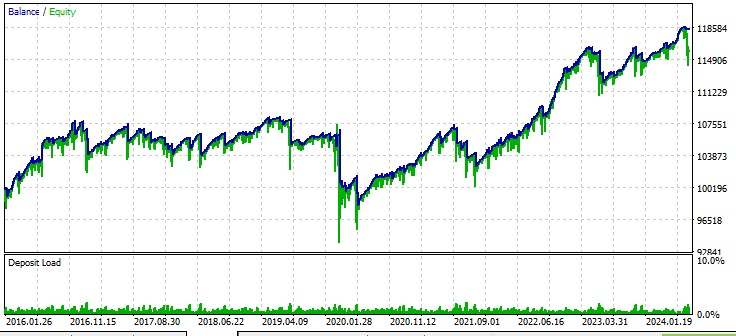
第三个货币对，GBPUSD：

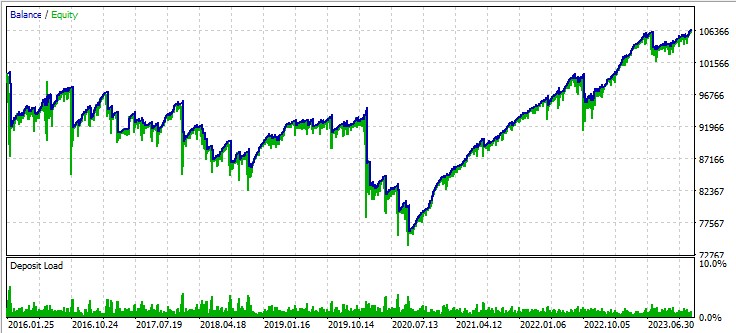
下一步行动

基于混沌理论的 EA 的进一步发展将需要深入的测试和优化。需要在不同的时间框架和金融工具上进行大规模测试，以更好地了解其在不同市场条件下的效率。使用机器学习方法可以帮助优化 EA 参数，提高其对不断变化的市场现实的适应性。

应特别注意改进风险管理系统。实施考虑当前市场波动和混乱波动预测的动态头寸大小管理，可以显著提高策略弹性。

结论

在本文中，我们研究了混沌理论在金融市场分析和预测中的应用。我们研究了相空间重构、确定最佳嵌入维数和时间延迟、以及最近邻预测方法等关键概念。

我们开发的 EA 展示了在算法交易中使用混沌理论的潜力。对各种货币对的测试结果表明，该策略能够产生利润，尽管在不同的工具上取得了不同程度的成功。

然而，值得注意的是，将混沌理论应用于金融领域会带来许多挑战。金融市场是一个极其复杂的系统，受到许多因素的影响，其中许多因素在模型中很难甚至不可能考虑在内。此外，混沌系统的本质使得长期预测从根本上不可能 — 这是严肃研究人员的主要假设之一。

总之，虽然混沌理论不是市场预测的圣杯，但它确实代表了金融分析和算法交易领域进一步研究和发展的一个有前景的方向。很明显，将混沌理论方法与机器学习和大数据分析等其他方法相结合，可以开辟新的可能性。