频域中的滤波和特征提取

概述

在金融市场领域，精准的预测模型备受追捧。可靠的预测模型需要有意义且相关的信息。在本文中，我们将探讨在频域中使用各种数字滤波器的应用，作为特征提取的工具。我们将涵盖离散傅里叶变换（DFT）把时间序列转换为频域进行分析的一些优点和缺点。将讨论三种类型的数字滤波器：同相、正交、和正交镜滤波器。强调每种类型在时间序列分析中的效用。最后，将提供实现每种类型的示例代码。

频域滤波

在文章《面向初学者的 MQL5 数字过滤器的实际实现》一文中，作者阐述了通过卷积在时域中应用的数字滤波器。该系列是一组不同长度的唯一权重的乘积，具体取决于滤波器类型及其参数。权重数量定义了一个移动窗口，当滤波器应用于该数据范围时，会与相应的序列值进行卷积。移动平均线也以相同的方式工作。

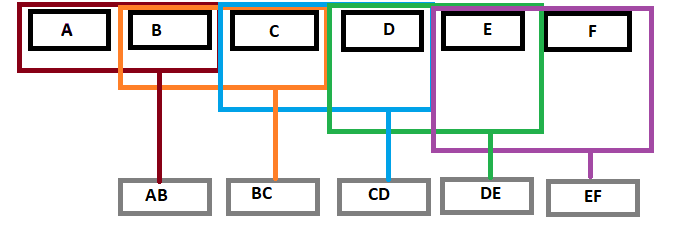
在本文中，我们将把滤波器应用在频域之中。涉及的基本步骤如下：

1.  首先，在准备 DFT 操作时对序列进行预处理。
2.  DFT 使用快速傅里叶变换算法（FFT）应用于序列。
3.  接下来，我们遵照我们认为必要的任何方式操纵序列的波形。也就是说，应用了一个滤波器，从而修改了序列的原始波形。
4.  对修改后的波形进行逆 DFT 操作，将其转换回熟悉的时域。
5. 最后，我们撤销在初始预处理步骤所执行操作所带来的任何影响。

与时域中的卷积类似，序列的 DFT 项乘以定义特定滤波器的系数。所涉及的众多步骤似乎表明，在频域中进行滤波的计算成本要高得多。但情况并非总是如此。

在处理大型数据集时，采用快速傅里叶变换（FFT）算法实际上比在时域中卷积序列要快得多。当适配某些最佳实践时尤其如此，我们将在另一章节中视察。

滤波器形状和函数

滤波器由一个函数确定，其输出可以根据滤波器的规范进行操纵。操纵函数的输出会改变滤波器的形状。滤波器的形状是滤波器的响应曲线。它控制滤波器在频域中的行为方式。在不同的研究领域中，信号处理中使用了众多滤波器形状。在时间序列分析中，首选带有圆角的滤波器。

带有圆角的滤波器具有独有的特征，这对于时间序列分析非常宝贵。圆角提供更平滑的频率响应。这有助于最大限度地减少频率分量之间转变时明显的失真。滤波器形状中的圆角表明在现实世界中更容易真实实现。因为它们的设计基于数学近似值，通常提供更好的性能。因此，其在区分有用和不需要的频率分量的能力，与最小化失真之间取得了良好的平衡。

高斯函数是本演示中重点要讲述的滤波函数。它的形状往往更集中在时域当中。表明与其它滤波函数相比，它的持续时间相对较短。在选择合适的滤波函数时，需要考虑许多权衡因素。在此，应用程序需求优先。

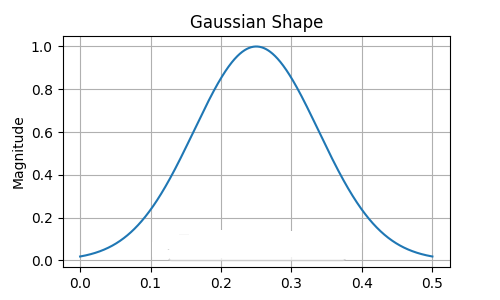
滤波器规范

本文中遇到的滤波器都由两个参数指定。中心频率和宽度参数。有时称为标尺。两者都应以每次抽样的频率周期来给出。中心频率的值可以在 0 到 0.5 之间。宽度参数决定了将通过滤波器函数的通带中高于和低于中心频率的频率范围，这些频率将相对不变。宽度值应取约为 0.01 及以上。

同相滤波器

我们从同相滤波器开始探索滤波器类型。波形在时间中的位置称为其相位。同相滤波器保持输入信号与输出信号的相位关系。这意味着当输入信号通过同相滤波器时，滤波后的输出将在允许的频率范围内保持与输入相同的时间关系。

带通滤波器是一种同相滤波器，可作为许多其它滤波器的基本构造模块。滤波器允许特定范围的频率通过，同时衰减或抑制该范围之外的频率。它通过减少频率低于或高于通带的信号来工作。

低通和高通滤波器是通过修改带通滤波器实现的。低通滤波器强调信号中的低频。主要用于检测过程的一般趋势。中心频率越低，滤波后的输出越平滑。使用带通滤波器函数，我们将所有小于或等于中心频率的频率乘以常数 1.0，并相应地衰减之上的所有其它频率。 

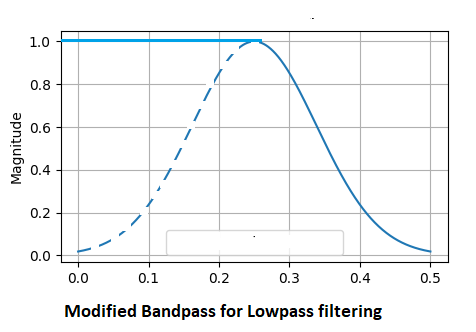
高通滤波器可消除信号中的所有低速波动，仅留下有关快速变化的信息。在这种情况下，低于中心频率的所有较低通带频率都会降低。只留下较高频段的频率通过。

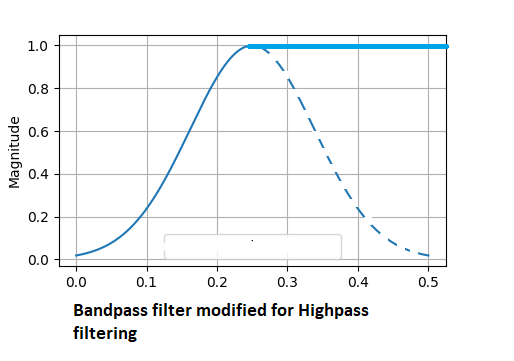
同相滤波器有许多变体，其中一些可能比迄今为止描述的要更好。这里提到的那些都具有足够圆形的滤波器形状的主要特性，这是一个重要的品质，怎么强调都不为过。  

正交滤波器

这些滤波器（也称为正交滤波器）设计在处理信号时相对于输入应用了 90 度（Pi/2 弧度）的相移。它们只是偶尔在孤立时有用，且更常与同相滤波器结合使用。在某些状况下，它们可用于检测时间序列内的相位关系。

为了理解正交滤波器的值，最好来观察一个示例。下面是一个由短周期分量描绘的序列。

下一张制图是上述序列的带通滤波输出。它强调了带通滤波器的同相特性。滤波信号中的走势与原始序列的走势一致。

下图显示的是带通滤波器的正交版本的滤波输出。仔细查验能够看出，滤波信号中的峰值对应于原始信号中的零轴交叉。基本上，正交滤波输出与应用于同相带通输出的位移对齐。

这意味着，正交输出信号中的峰值表明输入序列发生了显著变化。正交滤波器的波峰和波谷表示输入信号中发生的快速变化。或是，当输入信号稳定时，输出将为零、或接近零。这意味着正交滤波器对于特定速率下发生的变化很敏感。

我们来看另一个例子。以下序列的特点是急剧且突然地向上移动。

接下来是该序列的同相和正交滤波输出。同样，注意波峰和波谷相对于急剧向上移动的位置。而使用同相输出很难判定移动，但正交滤波序列可以检测到爆发性移动。

这两种类型滤波器的使用方式带来了曙光，它们一同使用时的效用。当具有相同参数的同相和正交滤波器一同使用时，它们被称为正交镜滤波器（QM 滤波器）。

正交镜滤波器

QM 滤波器有助于周期性分量的局部实例检测。使用 QM 滤波器，我们分析了相对于正交输出的同相输出。当不存在特定的周期性事件时，这两个输出都将为零。通过将同相输出视为实部，将正交输出视为虚部，可以将两者的输出进行组合。允许计算经滤波后波形的幅度和相位。

在我们查看代码的实现之前，我们必须首先处理任何时间序列分析过程的最重要方面之一。

在转换之前对序列进行预处理

时间序列的长度是有限的，这在使用 DFT 将它们转换为频域时会带来问题。DFT 假定原始序列是周期性的，因此会无限期地重复。将 DFT 应用于非周期性信号可能会导致输出波形失真。

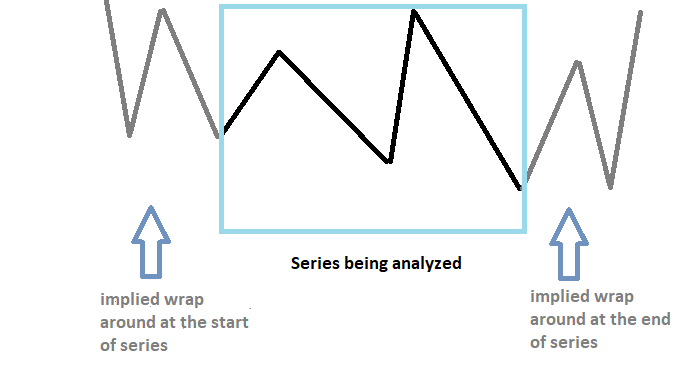
为了减轻环绕效应，我们必须用额外的常数值逐渐缩窄序列的末尾。人为地增加序列中的取样数量，可以提供更精细的频率分辨率，并减少频谱泄漏。这是一项称为填补的操作。带填补的序列使用 DFT 进行转换。该序列的额外值有助于减少该序列频谱的失真，但这些并不是唯一的好处。

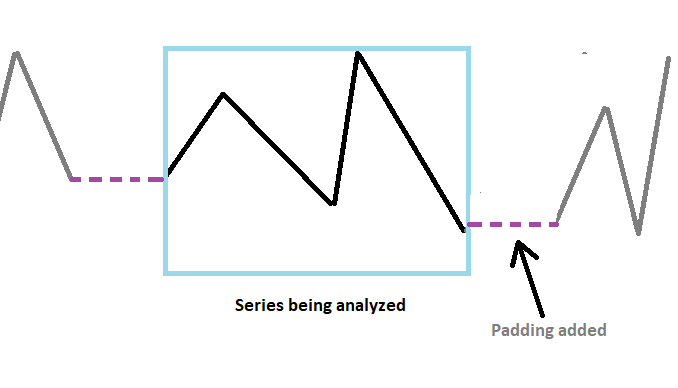
增加序列的长度，令取样总数为 2 的幂，极大地提高了 FFT 算法的计算效率。最初，故意增加长度会带来更好的性能看似很奇怪，但这是真的。故此，填补是基操。除了填补零值，还可以用计算出的序列平均值填补序列。

金融时间序列通常有一个令人讨厌的习惯，即非稳态。当一个序列经填补，并且该序列包含一个缓慢变化的分量时。原始序列两端的值与用于填充的值的鲜明对比，可能表现为频域中突出的频率分量。造成污染。

为了抗衡这种形式的失真，必须对原始序列值进行去趋势化。故此，原始序列值将替换为去趋势化之后的数值。当我们需要回到序列的原始时域时，我们只需要重新调整序列的趋势。我们将在下一章节中通览代码的实现时会演示这一点。

CFilter 类

CFilter 类封装了所讨论的三种滤波器类型的基本示例。代码包含在 Filter.mqh 当中，它首先包含来自 ALGLIB 函数库的 fasttransforms.mqh。

//+------------------------------------------------------------------+
//|  CFilter - class implementing select filters in the freq domain  |
//+------------------------------------------------------------------+
class CFilter
  {
   int               m_length;                   //length of original series
   int               m_padded_len;                //modified length of series
   int               m_half_padded_len;           //half of modded series
   double            m_slope, m_intercept;     //slope and intercept of trend in series
   double            m_buffer[];               //general internal buffer
   bool              m_initialized;              //initialization flag
   complex           m_dft[];                 //general complex buffer

public:
                     CFilter(double &series[],uint min_padding=0, bool detrend=true);
                    ~CFilter(void);

   void              Lowpass(double freq,double width,double &out[],bool add_trend);
   void              Highpass(double freq,double width, double &out[]);
   void              Bandpass(double freq,double width, double &out[]);
   void              Qmf(double freq,double width, complex &out[]);
   bool              IsInitialized(void) { return m_initialized; }
  };

CFilter 有一个参数化构造函数，用户必须把需要滤波的原始序列传递给该构造函数，还有另外两个参数，即指定要应用的填补量，以及在应用 DFT 转换之前是否要针对序列进行去趋势化。如果将 “min_padding” 设置为零，则实际填补数量仅由取样数量判定。“min_padding” 判定添加到序列中的最小值数量，排除包含的任何额外值，从而将序列延申到最接近的 2 的幂。

在构造函数内部，在检查所有参数之后，计算出填补序列的最终长度，如果已指定，则应用去趋势化。填补的序列被写入 “m_buffer” 数组。DFT 与 “m_dft” 中给出的序列波形一起应用，它是一个复数数组。如果在构造函数中遇到任何错误，“m_initialized” 将设置为 false。

//+------------------------------------------------------------------+
//|constructor                                                       |
//+------------------------------------------------------------------+
CFilter::CFilter(double &series[],uint min_padding=0,bool detrend=true)
  {
//---local variables
   m_initialized=false;
   int i;
   int npts = ArraySize(series);
   int pad = (int)MathAbs(min_padding);
//--- check size of series
   if(npts<=0)
     {
      Print("Input array is empty");
      return ;
     }
//---
   m_length = npts ;
   for(m_padded_len=2 ; m_padded_len<INT_MAX ; m_padded_len*=2)
     {
      if(m_padded_len >= npts+pad)
         break ;
     }
//---
   if(m_padded_len<npts+pad)
     {
      Print("Warning, calculated length of modified series is too long");
      return;
     }
//---
   m_half_padded_len = m_padded_len / 2;
//---
   ArrayResize(m_buffer,m_padded_len);
//---
   if(m_padded_len > npts)            // Any padding needed?
     {

      if(detrend)
        {
         m_intercept = series[0] ;
         m_slope = (series[npts-1] - series[0]) / (npts-1) ;
        }
      else
        {
         m_intercept = m_slope = 0.0 ;
         for(i=0 ; i<npts ; i++)
            m_intercept += series[i] ;
         m_intercept /= npts ;
        }

      for(i=0 ; i<npts ; i++)
        {
         m_buffer[i]=series[i] - m_intercept - m_slope * i ;
        }
      for(i=npts ; i<m_padded_len ; i++)
        {
         m_buffer[i]=0.0;
        }
     }

   else
     {
      ArrayCopy(m_buffer,series);
      m_intercept = m_slope = 0.0 ;
     }
//---Compute the Fourier transform of the padded series
   CFastFourierTransform::FFTR1D(m_buffer,int(m_padded_len),m_dft);
//---
   m_initialized = true;

  }

用户应通过调用 “IsInitialized()” 来检查实例是否已被正确构造。成功时它应该返回 true。

成功实例化之后，用户可以调用任何可公开访问的方法，依据存储在 “m_dft” 中的信号应用指定的滤波器。其中大多数都有类似的输入要求。首先是滤波器规范，由 “freq” 和 “width” 参数定义。它们对应于欲应用的通带中心频率和宽度。几乎所有方法都期待至少有一个最后输入数组，滤波操作的结果会保存在其中。

“Lowpass()” 是唯一接受第四个输入参数的方法，该参数判定最初应用于原始信号的任何去趋势化是否应在滤波器的输出上逆转。

//+--------------------------------------------------------------------+
//|Filters series in frequency domain and returns output in time domain|
//+--------------------------------------------------------------------+
void CFilter::Lowpass(double freq,double width,double &out[],bool add_trend)
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=0 ; i<=m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;  // This frequency
      if(f <= freq)                  // Flat to here
         wt = 1.0 ;
      else
        {
         dist = (f - freq) / width ;
         wt = exp(-dist * dist) ;
        }
      dft_temp[i].real*=wt;
      dft_temp[i].imag*=wt;
     }
//---
   double temp[];
//---
   CFastFourierTransform::FFTR1DInv(dft_temp,m_padded_len,temp);
//---
   ArrayResize(out, m_length);
//---
   for(int i = 0; i<m_length; i++)
      out[i]=(add_trend)?temp[i] + m_intercept + m_slope*i:temp[i];

  }

 同相滤波器的实现涉及两个步骤：首先，将放置在 “m_dft” 中的信号波形与修订后的滤波器函数相乘。在该实现中，它是高斯函数。最后，进行逆 DFT，将序列返回到时域。 

为了计算 QM 滤波器输出，我们将波形的 DFT 项乘以滤波器函数的正交版本。同正交滤波器函数只是应用了同相滤波器函数的 90 度相移。为了达成这种相移，同相滤波器函数乘以 i，令其成为纯虚数。结果是一个函数，其输出与奈奎斯特（Nyquist）频率对称。0.5 频率两侧的输出项在绝对值上相等，但符号相反。

“Qmf()” 方法事实上是通过将波形的 DFT 项乘以同相和正交滤波器函数的总和。这是令正交滤波函数作为纯实数，（回想一下，正交滤波函数是纯虚数）乘以 i。当滤波器函数相加时，超出奈奎斯特频率的输出会相互抵消。在代码中，高于 0.5 的过滤 DFT 项设置为 0。只需计算低于奈奎斯特频率，且等于奈奎斯特频率的滤波输出。一旦波形被滤除，复杂的逆 DFT 结束，并返回到时域。

//+------------------------------------------------------------------+
//| Implements Quadrature Mirror Filter, output is complex           |
//+------------------------------------------------------------------+
void CFilter::Qmf(double freq,double width,complex &out[])
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=1 ; i<m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;    // This frequency
      dist = (f - freq) / width ;
      wt = exp(-dist * dist) ;
      dft_temp[i].real *= wt ;
      dft_temp[i].imag *= wt ;
      dft_temp[m_padded_len-i].real = dft_temp[m_padded_len-i].imag = 0.0 ;  // Causes QMF outputs
     }

//---
   dft_temp[0].real = 0.0 ;
   dist = (0.5 - freq) / width ;
   dft_temp[m_half_padded_len].real = 0.5 * dft_temp[m_half_padded_len].imag * exp(-dist * dist) ;
//---
   dft_temp[0].imag = dft_temp[m_half_padded_len].imag = 0.0 ;     // By definition of real transform
//---
   CFastFourierTransform::FFTC1DInv(dft_temp,m_padded_len);
   ArrayResize(out,m_length);
//---
   for(i=0 ; i<m_length ; i++)
     {
      out[i].real = dft_temp[i].real/double(m_half_padded_len) ;
      out[i].imag = dft_temp[i].imag/double(m_half_padded_len) ;
     }
  }
//+------------------------------------------------------------------+

AFD 程序

为了演示运用 CFilter，我们引入了 AFD.mq5。作为智能交易系统实现的应用程序。它令用户能够生成指定长度的随机序列。用户可以设置要生成的序列长度，还可以调整所用随机数的种子。该序列在上图中以蓝色绘制。用户可以在第二个图中观察所选定滤波器应用于生成的序列的结果。滤波器的所有参数都可以从程序的图形用户界面中进行调整。该应用程序如下所示。

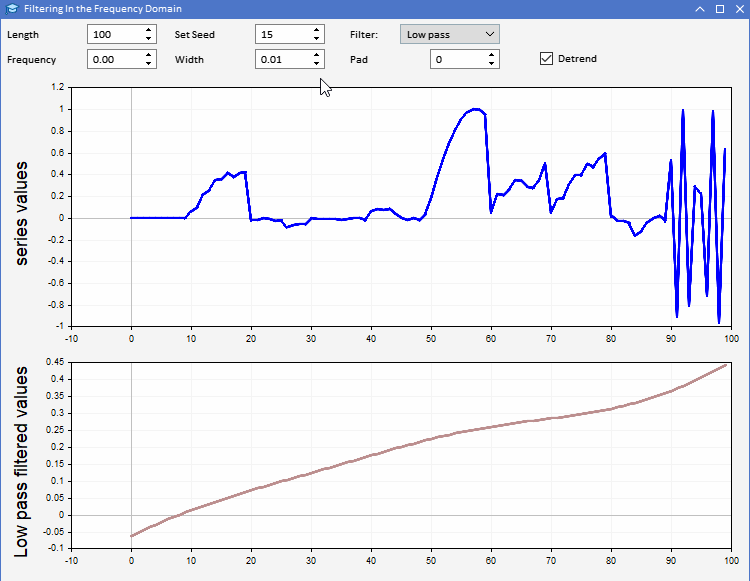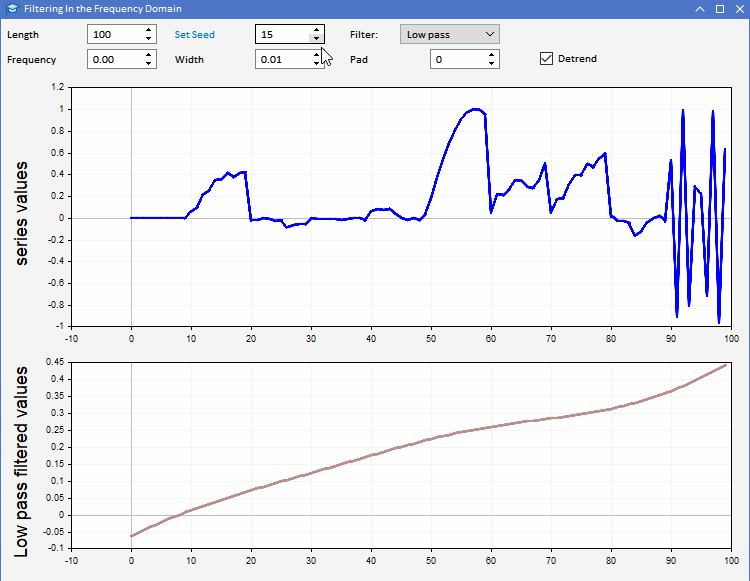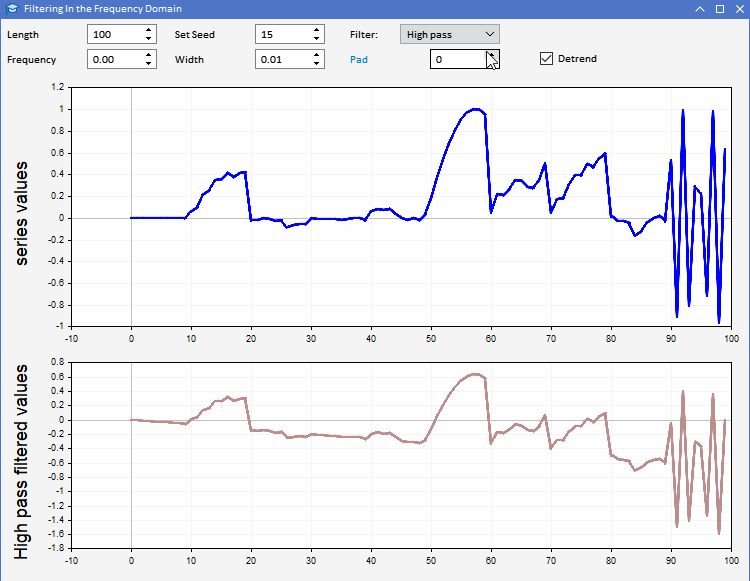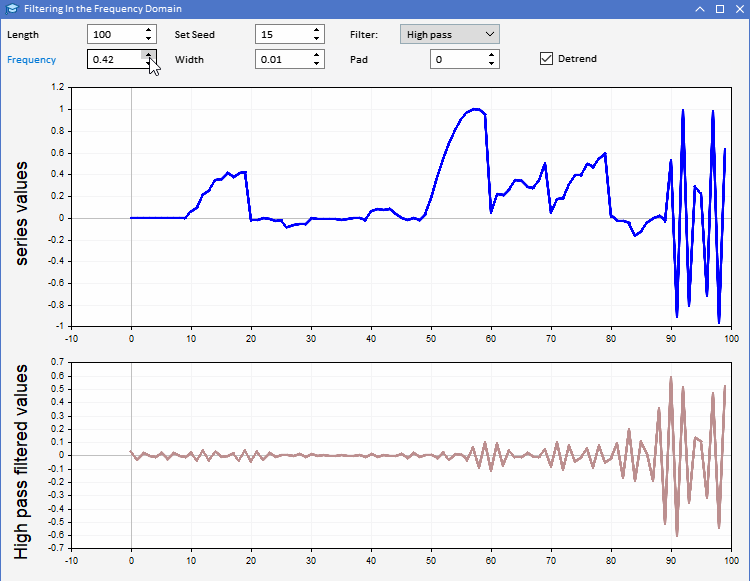
使用 AFD 应用程序，我们可以更直观地了解滤波器输出所揭示的不同类型的信息。同相滤波器的输出可以通过两种方式使用。低通滤波器的输出可用于提供有关任何给定时间输入序列的平均值的信息。高通滤波器输出揭示了原始序列中偶尔出现的高点和低点。这些输出提供了每个时间点输入序列的状态感知。

带通滤波器输出的相关性不太明显。对于任何人来说，仅通过观察都不可能理解滤波器的输出。尽管这些数据可能对预测模型有用。也许知道特定通带的带通输出处于峰值或低谷意味着原始序列中的某些含义。

我们看一下随机序列在不同频率下的带通输出。

输出揭示了另一种类型的信息。带通输出的峰值描绘了特定时隙的周期性变化量。更准确地说，它展示出变化的幅度，表明存在周期性变化。较低的峰值表示较小的变化，而较高的峰值则表示相反的变化。

振幅是通过对 QM 滤波器输出进行采样得到的。利用 QM 滤波器值的幅度和相位计算显示在下面的代码片段中，该代码片段取自 AFD.mq5。

 case ENUM_QMF_AMPLITUDE:
        {
         y_name = "Amplitude";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=MathSqrt(comp[i].real*comp[i].real + comp[i].imag*comp[i].imag);
        }
      break;
      case ENUM_QMF_PHASE:
        {
         y_name = "Phase";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=(comp[i].real>=1.e-40 || comp[i].imag>=1.e-40)?atan2(comp[i].imag, comp[i].real):0.0;
        }
      break;

不同频率下带通输出的差异表明，可用的信息是多种多样的。因此，可以构建独特的特征，从而提供给机器学习算法。为了智能地构建这些数据集，从业者需要牢牢掌握定义特定过滤器的参数。

width 参数

如本文前面所述，所有实现的滤波器的参数都以每单位时间的频率周期表示。在频域中进行分析的一个缺点是难以将频率分量与其在时域中的程度相关联。以上一章节中刚刚看到的随机序列为例，带通输出的采样频率为 0.15、0.3 和 0.45，宽度均为 0.03。理解这些值的含义非常重要，尤其是与序列的时域相关的数值。

频率为 0.15 的周期为 1/0.15 = 每个周期 6.67 次取样。宽度决定了频域中的分辨率。如果我们想隔离一个窄频带，我们应用一个小宽度，0.01 通常是最小值，尽管可以更低。再次回到这个例子。宽度设置为 0.03，因此通带从 0.15-0.03 延伸到 0.15+0.03，即 0.12 到 0.18。这个范围内的频率将允许通过，高于和低于的频率则几乎完全停止。

宽度还表示了时域中的分辨率。频域分辨率和时域分辨率之间的关系呈反比。一个域中的分辨率较高，会导致另一个域中的分辨率损失。为了估算时域范围相对于宽度，我们应用以下公式：0.8/width

使用它，我们可以估算时域中的取样数量受到的相对于当前位置频率通带的影响。换言之，它估算了当前位置之前和之后的取样数量，这些取样数量将对观察到的输出产生影响。回到示例，宽度为 0.03 表示时间范围为 0.8/0.03 = 27 次取样。这意味着每个输出的值都由之前的 27 个观测值和之后的另外 27 个观测值判定或影响。

一般来说，滤波器的宽度应该与我们希望研究的通带的中心频率成正比。这与频率的周期有关。较低频率的周期较长，而较高频率的周期较短。因此，对于较低的频率，我们可以牺牲时域分辨率，并选择较窄的宽度。而更高的频率受益于更宽的宽度参数，而这意味着在时域中的范围更短。

最后，width 参数也会对提供给预测模型的数值产生影响。使用前一个示例，我们计算出的隐含时域大约为 27 次观测值。假设我们想预测序列的下一个值，在时隙编号 201。我们将提供根据 200 个已知值计算出的滤波输出的值，即从序列末尾开始的 27 个时隙。我们不能故意使用超过此点的任何滤波输出，因为我们知道，在滤波器参数的约束下，它会受到 DFT 引起的环绕效应的影响。

在最后一个示例中，我们针对不同频率的滤波输出进行采样，但所有频率都具有相同的宽度。在实践中，在策略性选择的频率和宽度上针对滤波输出进行采样会更有益处，从而捕获尽可能多的有用信息。

结束语

总之，我们研究了三种类型的滤波器：

• 同相滤波器有助于将噪声序列分解为不同的分量，突出重要信息，并消除分散注意力的多余特性。通过给学习算法提供相关信息，我们可以构建更好的预测模型。

• 正交滤波器可用于检测序列中级别快速变化的区域。尽管也许很容易注意到一序列中的重大走势，但将此类现象传达给学习算法可能很困难。这就是正交滤波器的价值。

• 同相滤波器和正交滤波器的共同组合作用，从而识别周期性特征的存在。这些工具可以有效地识别和研究在时间序列中以看似随机的方式表现出来的特征。

频域滤波利用了 FFT 算法提供的计算效率。与时域中的卷积方法相比，这是没有争议的。但是，这并不全是玫瑰。将序列变换到频域充满了陷阱，由于粗心的数据处理导致的失真，能导致完全错误的结论。所以从业者应该保持警惕。

所有工具和程序的代码都附于文后。AFD.mq5 利用了古老的 Easy and Fast（EAF）GUI 函数库。它可以在 mql5.com 的代码库中找到。顺便说一句，当使用 EAF 和 ALGLIB 函数库时，请始终确保在应用程序中最后包含 EAF，这些函数库之间存在一些命名冲突，这会阻碍成功编译。  

文件名	说明
Mql5\Include\Filter.mqh	包含 CFilter 类的定义，该类在频域中实现基本数字滤波器
Mql5\Include\RandomStationarySeries.mqh	包含生成各种特性的随机序列的例程（函数）。用于 AFD.ex5 应用程序
Mql5\Experts\AFD.mq5	这是 AFD 应用程序的源代码，它使用 mql5.com 代码库中列出的 Easy and Fast GUI 函数库
Mql5\Experts\AFD.ex5	编译的 AFD 应用程序，作为智能系统实现