神经网络变得轻松（第三十三部分）：分布式 Q-学习中的分位数回归

内容目录

• 概述
• 1. 分位数回归
• 2. 以 MQL5 实现
• 3. 测试
• 结束语
• 参考
• 本文中用到的程序

概述

在上一篇文章中，我们领略了分布式 Q-学习，它允许学习预测奖励的概率分布。 我们已学会了如何预测在特定数值范围内获得预期奖励的概率。 但是这种范围的数量和奖励值的分布是模型的超参数。 因此，需要有关奖励值分布的专业知识才能选择最优参数。 我们还需要进行某些测试来选择最优的超参数。

必须说，将整个可能数值范围划分为相等范围的方式（我们之前曾研究过）也有其缺点。 我们鉴别一个神经元来预测每个动作在每个单独范围内获得奖励的概率。 然而，在实践中，在大数据范围内所获奖励等于零的概率十分平常。 这意味着我们的资源利用率十分低效。 我们可以合并一些范围来减少操作次数。 这样能加快模型训练和执行。 与此同时，在其它范围内获得奖励的概率也相当高。 为了获得更完整的全景图，我们可将此范围分解为更小的元件。 这将提高预测预期奖励的准确性。 不过，我们的方式不支持不同尺寸范围的创建。 这些缺点可以运用于 2017 年十月在文章“使用分位数回归的分布强化学习”中提出的分位数回归算法来解决。

1. 分位数回归

分位数回归针对解释变量的分布与目标变量的某些分位数之间的关系进行建模。

在我们继续研究分位数回归在分布式 Q-学习中的使用之前，应该提到的是，所提出的算法接近于来自另一侧期望奖励的概率分布评估。 以前，我们将可能的奖励值范围划分为不同的区域。 在新算法中，我们将得到的奖励集合划分成几个概率相等的分位数。 这样做有什么益处？

我们仍然有一个分析分位数的超参数。 但与此同时，我们不限制可能的奖励价值范围。 取而代之，我们训练模型来预测分位数的中值。 由于我们用的是等概率分位数，因此我们不会有零概率奖励的分位数。 甚至，在稀疏奖励值区域，我们将获得更大的分位数。 在会有很多奖励的所在，分位数将被分解成更小的部分。 因此，我们可以更全面地了解期望奖励的概率分布。 甚而，这种方法能够识别稀疏的非静态区域和增加的奖励值密度。 它们可能因环境状态而异。

然而，它仍然是相同的 Q-学习。 该过程本身基于贝尔曼（Bellman）优化方程。

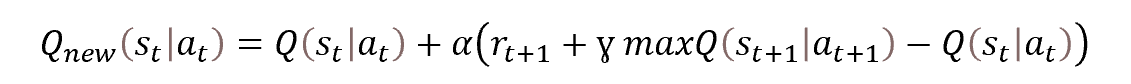
不过，这次我们必须定义的不是一个值，而是整个分布。 但基本上，任务保持相同。 我们来仔细查看这个任务。

如上所述，我们将训练样本的整个奖励分布划分为 N 个等概率分位数。 每个分位数的等级不可由给定概率的所分析随机变量超过。 在此，等同得可能分位数是具有固定步长的分位数，而它们的总集涵盖了整个训练数据集。

在实践中，当我们有一个训练数据集时，从数据集中获取其中一个元素的概率为 1。 不能有任何其它选项，因为所有元素都应取自训练数据集。

将集合拆分为 N 个等概率分位数，这意味着将整个训练数据集拆分为 N 个相等的部分。 它们中的每一个部分都包含相同数量的元素。 从其中一个子集中选择元素的概率为 1/N。

单独的分位数由 2 个参数表征：选择元素的概率，及其元素值的上限。 分位数的另一个条件是它们随概率的累积按升序排序。 这意味着每个后续分位数的值上限高于前一个分位数。 分位数的概率包括以前分位数的概率。 例如，对于某个分布，我们的分位数为 0.2，等级 15。 这意味着整个分布中 20% 的元素值不超过 15。 概率的步长和最大分位数值的等级可能不成比例，因为它们取决于特定的分布。

我们正在研究的算法涉及将数据集拆分为具有固定概率步长的分位数。 我们将训练模型来预测分位数的中值，取代上限。

为了训练模型，我们需要目标值。 拥有某个数据集的完整元素集，我们就可以很容易地找到平均值。 

但我们在实践中不会得到完整一套。 只有在执行动作，并过渡到新状态之后，我们才会从环境中获得奖励。 如您所见，使用新的模型训练算法不会影响与环境的交互。 在最初的 Q-学习中，我们训练模型来预测平均预期奖励。 为了做到这一点，我们通过迭代将模型的结果转移到具有较小学习系数的目标值。 如您所见，在学习过程中，我们的模型结果持续受到朝当前目标值的偏转力的影响。 当多向合力相互平衡的那一刻达到平均值（如图所示）。

我们可以用类似的方式来解决新算法的问题。 但有一件事。 此算法允许您找到集合的平均值。 这就是 0.5 的分位数。 当以最纯粹的形式应用它时，我们将在模型结果层的所有神经元上得到相同的值。 它们都将同步工作，如同一个神经元。 不过，我们需要获得所分析分位数上值的真实分布。

查看分位数的性质。 例如，考虑分位数 0.25，这是分析数据集的四分之一。 如果我们舍弃元素值之间的距离，那么对于分位数的每 1 个元素，总集合中应该有 3 个元素不属于这个分位数。 回到我们上面的例子，为了在 0.25 分位数点实现平衡，推动数值减小的力度必须是推动分位数的值增长力度的 3 倍。

因此，为了找到每个特定分位数的值，我们应该在贝尔曼方程中引入一个校正因子。 该因子将取决于分位数等级和偏离方向。

其中 τ 是分位数的概率特征。 

在学习过程中，我们以经验再现和目标网络的形式来运用经典 Q-学习算法的所有启发式方法。

2. 以 MQL5 实现

在研究了算法的理论方面之后，我们继续讨论本文的实施部分。 我们将研究如何以 MQL5 实现算法。 在实现算法时，我们不会创建新的神经层架构。 然而，我们会将流程组织到一个单独的类 CQRDQN 当中。 这将简化该方法在智能系统中的使用，并将保护用户免受某些实现细节的影响。 新类的结构如下所示。

class CQRDQN : protected CNet
  {
private:
   uint              iCountBackProp;
protected:
   uint              iNumbers;
   uint              iActions;
   uint              iUpdateTarget;
   matrix<float>     mTaus;
   //---
   CNet              cTargetNet;
public:
   /** Constructor */
                     CQRDQN(void);
                     CQRDQN(CArrayObj *Description)  { Create(Description, iActions); }
   bool              Create(CArrayObj *Description, uint actions);
   /** Destructor */~CQRDQN(void);
   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) 
                       { return        CNet::feedForward(inputVals, window, tem); }
   bool              backProp(CBufferFloat *targetVals, float discount,
                              CArrayFloat *nextState, int window = 1, bool tem = true); 
   void              getResults(CBufferFloat *&resultVals);
   int               getAction(void); 
   int               getSample(void);
   float             getRecentAverageError() { return recentAverageError; } 
   bool              Save(string file_name, datetime time, bool common = true)
                       { return        CNet::Save(file_name, getRecentAverageError(),
                                                  (float)iActions, 0, time, common); }
   virtual bool      Save(const int file_handle);
   virtual bool      Load(string file_name, datetime &time, bool common = true);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)   const   {  return defQRDQN;   }
   virtual bool      TrainMode(bool flag) { return CNet::TrainMode(flag); } 
   virtual bool      GetLayerOutput(uint layer, CBufferFloat *&result) 
     { return        CNet::GetLayerOutput(layer, result); }
   //---
   virtual void      SetUpdateTarget(uint batch)   { iUpdateTarget = batch; }
   virtual bool      UpdateTarget(string file_name);
   //---
   virtual bool      SetActions(uint actions);
  };

新类派生自 CNet 类，该类把我们的神经网络模型操作组织到一起。 这意味着我们将构建一个新算法来操作该模型。

为了存储算法的关键参数，我们将创建以下变量：

• iNumbers — 集合中描述一个动作分布的神经元数量
• iActions — 可能动作变体的数量
• iUpdateTarget — 模型更新频率参数 目标网络
• mTaus — 写入分位数概率特征的矩阵
• cTargetNet — 指向 目标网络 对象的指针

请注意，在 mTaus 矩阵中，我们写入每个分位数概率的中值。

在类构造函数中，设置这些变量的初始值。

CQRDQN::CQRDQN()  :  iNumbers(31),
                     iActions(2),
                     iUpdateTarget(1000)
  {
   mTaus = matrix<float>::Ones(1, iNumbers) / iNumbers;
   mTaus[0, 0] /= 2;
   mTaus = mTaus.CumSum(0);
   cTargetNet.Create(NULL);
   Create(NULL, iActions);
  }

与组织神经网络模型的 CNet 类一样，除了没有参数的构造函数之外，我们还将创建一个方法，以我们正在创建的模型架构的规范重载。

                     CQRDQN(CArrayObj *Description)  { Create(Description, iActions); }

该方法将在 Create 方法中创建。 该方法在参数中接收指向数组的指针，该数组描述模型体系结构，和代理者可能的动作数量。

bool CQRDQN::Create(CArrayObj *Description, uint actions)
  {
   if(actions <= 0 || !CNet::Create(Description))
      return false;

在方法主体中，检查指定的代理者动作数量是否正确。 调用具有相同名称的父类方法。 它包括有关描述模型体系结构的对象的所有必要控制，并实现模型创建过程。 于此我们只检查父类操作的逻辑结果。

成功创建新模型后，获取所创建模型的结果层。 基于有关其大小和可能的代理者动作数量的信息，填写概率分位数特征的 mTaus 矩阵。 此矩阵中的行数等于一个动作的奖励概率分布的大小。 由于在训练开始之前设置的每个分位数的概率，对于具有相等固定步长的代理者的所有可能动作都是相等的，因此我们采用一行的向量矩阵即可。 我们采用矩阵而不是向量，因为解决方案将会进一步开发，稍后它可能意味着行动的可变概率分布。

   int last_layer = Description.Total() - 1;
   CLayer *layer = layers.At(last_layer);
   if(!layer)
      return false;
   CNeuronBaseOCL *neuron = layer.At(0);
   if(!neuron)
      return false;
   iActions = actions;
   iNumbers = neuron.Neurons() / actions;
   mTaus = matrix<float>::Ones(1, iNumbers) / iNumbers;
   mTaus[0, 0] /= 2;
   mTaus = mTaus.CumSum(0);
   cTargetNet.Create(NULL);
//---
   return true;
  }

请注意，在初始步骤中，我们重置目标网络。 以此方式可防止在训练新模型时，使用来自未经训练的模型的绝对随机值。

为了实现前馈验算，我们将调用父类的类似方法。

   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) 
                     { return CNet::feedForward(inputVals, window, tem); }

至于向后馈方法 backProp，我们需要稍微花点功夫。 我要提醒您，环境会对每个代理者动作反馈奖励。 在经典的 Q-学习过程中，我们定义了奖励政策。 由于交易当中代理者可能的行为会相互排斥，并且在本质上是相反的，我们可以通过环境为执行的动作返回的奖励来判定相反行为的奖励。 基于此功能，我们可以在每次后向验算时传递所有可能动作的目标值。 这令学习过程更快捷、更稳定。 但是在分布式 Q-学习过程中，我们正在应对每个动作的整个目标值向量。 在上一篇文章中，我们构建了一个在模型训练 EA 中创建模型目标张量的新流程。 我们还创建了一个新模块，在智能系统执行一个动过之前解码模型结果，以便检查已训练模型如何工作。

现在，通过创建一个新类，我们就可以对用户隐藏此过程。 故此，操控该模型将更简单、更清晰。 实际上，它类似于操控经典的 Q-学习，其中环境仅返回每个动作的离散奖励值，而把此离散奖励转换为每个动作的分布向量的整个过程则是在后向馈送方法的主体中实现。

我必须说一下使用新类来实现该过程的另一个优点。 如您所知，Q-学习过程是到目标网络来预测未来的奖励。 以前，用户必须操控两个模型。 现在我们可以将目标网络的所有工作隐藏在我们的类方法之中。 这将令操作更加舒适。 然而，这需要更改后向馈送方法的参数。 在这种情况下，为了正确执行反向传播（后向馈送）验算，我们希望从用户那里接收目标值，以及系统的新状态。

在后向验算方法的主体中，我们首先检查接收到的目标值向量指针的正确性。 此外，生成的向量大小应等于可能的代理者动作数量。

bool CQRDQN::backProp(CBufferFloat *targetVals, float discount,
 CArrayFloat *nextState=NULL, int window = 1, bool tem = true)
  {
//---
   if(!targetVals)
      return false;
   vectorf target;
   if(!targetVals.GetData(target) || target.Size() != iActions)
      return false;

然后，我们检查指向描述新系统状态的向量指针的正确性。 如有必要，我们会实现一个前馈验算目标网络。 之后，我们判定最大可能的奖励，并参考折扣因素调整从环境中获得的未来收入奖励。

   if(!!nextState)
     {
      if(!cTargetNet.feedForward(nextState, window, tem))
         return false;
      vectorf temp;
      cTargetNet.getResults(targetVals);
      if(!targetVals.GetData(temp))
         return false;
      matrixf q = matrixf::Zeros(1, temp.Size());
      if(!q.Row(temp, 0) || !q.Reshape(iActions, iNumbers))
         return false;
      temp = q.Mean(0);
      target = target + discount * temp.Max();
     }

我们将采用以下公式来更新模型参数。

不过，请注意，在方法主体中实现上述公式时，我们不会用到学习因子。 这有个小窍门。 关键是，在方法主体中，无论看起来多么奇怪，我们都不会更新模型参数。 我们只为模型创建目标结果向量。 而模型参数将在父类方法（具有相同的名称）中更新。 我们将目标模型结果的完整张量传递给父类方法。 更新模型参数时，我们要参考学习系数。

在这一步，我们已经从环境中获得了回报，包括可能的未来收益。 若要创建目标值的向量，我们只需要模型前馈验算的最新结果。 它们将被加载到局部 Q 矩阵之中。 

   vectorf quantils;
   getResults(targetVals);
   if(!targetVals.GetData(quantils))
      return false;
   matrixf Q = matrixf::Zeros(1, quantils.Size());
   if(!Q.Row(quantils, 0) || !Q.Reshape(iActions, iNumbers))
      return false;

之后，我们可以为模型的目标值创建所需的缓冲区。 为此，我们将构建一个循环过程，该过程针对代理者的每个单独可能动作创建分位数等级的目标值向量。 请注意，在构建算法时，使用矩阵和向量运算需要一些技巧和方式的变化。 另一方面，它减少了循环的使用。 通常，这会增加程序执行速度。

在这种情况下，使用向量运算消除了使用嵌套循环系统的需要，在该系统中，我们将为每个可能的动作迭代所有动作和分布的所有元素。 取而代之，我们针对代理者的可能动作只使用 1 个循环。 在大多数情况下，循环迭代的次数比之消除的循环迭代次数要少几十倍。 但这样做的代价是我们不能使用条件运算符。 我们不可只比较向量的两个元素，并根据比较结果来选择动作。

我们不得不针对向量的所有元素执行全部操作分支。 为了不扭曲操作的预期结果，我们将创建两个差异向量，分别保存从环境中获取的奖励和上次前馈验算的结果。 之后，在一个向量中我们重置负数值，在第二个向量中我们重置正数值。 因此，将所获向量乘以为调整平均分位数值影响而设定的相应系数后，我们就得到所需的校正值。 所接收向量的总和，以及前馈验算的最后结果，将生成我们所需的模型后向验算的目标值。

   for(uint a = 0; a < iActions; a++)
     {
      vectorf q = Q.Row(a);
      vectorf dp = q - target[a], dn = dp;
      if(!dp.Clip(0, FLT_MAX) || !dn.Clip(-FLT_MAX, 0))
         return false;
      dp = (mTaus.Row(0) - 1) * dp;
      dn = mTaus.Row(0) * dn * (-1);
      if(!Q.Row(dp + dn + q, a))
         return false;
     }
   if(!targetVals.AssignArray(Q))
      return false;

一旦所有循环迭代完成后，更新目标值缓冲区中的数值。

接下来，我们将执行一个关于如何操控目标网络模型的小型辅助操作。 我们将实现一个后向验算迭代计数器。 当达到迭代次数阈值时，更新目标网络模型。

   if(iCountBackProp >= iUpdateTarget)
     {
#ifdef FileName
      if(UpdateTarget(FileName + ".nnw"))
#else
      if(UpdateTarget("QRDQN.upd"))
#endif
         iCountBackProp = 0;
     }
   else
      iCountBackProp++;

请注意达到后向验算迭代阈值时，比较运算符主体中的宏替换。 与以前一样，在更新目标网络模型时，我们不会直接将参数从一个模型复制到另一个模型。 取而代之，我们保存然后从文件中恢复模型。 若要实现此操作，我们需要一个文件名。

在我的所有模型中，我使用 FileName 宏替换来生成一个唯一的文件名，具体取决于智能系统、所交易的金融产品和所用的时间帧。 此宏替换直接在智能系统中分配。 此处实现的宏替换允许我们检查宏替换的分配，以便在智能系统中生成文件名。 如果生成了一个，我们就用它来保存和恢复文件。 否则，将采用默认文件名。

#define FileName        Symb.Name()+"_"+EnumToString(TimeFrame)+"_"+StringSubstr(__FILE__,0,StringFind(__FILE__,".",0))

在我们的方法结尾，我们调用父类的后向验算方法，并将准备好的目标结果张量作为输入参数。 父类方法操作的逻辑结果将返回给调用程序。

   return CNet::backProp(targetVals);
  }

因此，我们在执行后向验算时向用户隐藏了概率分布模型的使用。 对于每个操作，环境仅返回一个离散的奖励。 现在，调用反向馈送方法类似于经典的 Q-学习算法。 不过，我们为用户节省了控制第二个目标网络模型的需要。 我认为这增加了模型的可用性。 但前馈验算的问题仍然悬而未决。

如上所述，父类方法用于前馈方法。 而这不会直接对前馈操作产生负面影响，因为前馈验算方法仅返回操作的逻辑结果。 当尝试获取正向验算的结果时问题就会浮现。 父类方法将返回模型生成的完整概率分布。 在此，我们在前馈结果和后馈目标之间存在差距。 故此，我们必须重新定义获取前馈结果的方法，以便它们与反向验算目标值具有可比性。

这就是能得到等分概率分位数帮助的地方。 这令我们能够简单地从代理者的每个可能动作生成的整个分布中找到平均值，并将该值作为预期奖励返回。 在此，我们还调用矩阵运算，它可以在不使用循环的情况下构建整个算法方法。

在方法的开头，我们调用父类的同名方法，该方法实现了把前馈验算结果复制到数据缓冲区相关的所有必要控制和操作。 将获得的数据转至矩阵当中。 它们将矩阵重新格式化为表格矩阵，其行数等于可能的代理者动作数量。 在这种情况下，每一行都是一个向量，其中包含每个单独动作的预期奖励的概率分布。 因此，我们只需要一个矩阵函数 Mean 来确定代理者所有可能动作的平均值。 我们只需要将结果转移至数据缓冲区，并将其返回给调用方即可。

void CQRDQN::getResults(CBufferFloat *&resultVals)
  {
   CNet::getResults(resultVals);
   if(!resultVals)
      return;
   vectorf temp;
   if(!resultVals.GetData(temp))
     {
      delete resultVals;
      return;
     }
   matrixf q;
   if(!q.Init(1, temp.Size()) || !q.Row(temp, 0) || !q.Reshape(iActions, iNumbers))
     {
      delete resultVals;
      return;
     }
//---
   if(!resultVals.AssignArray(q.Mean(1)))
     {
      delete resultVals;
      return;
     }
//---
  }

您也许对此感到好奇，为什么我们要做这一切，如果回到平均值，即原始 Q-学习训练如何。 在不深入数学解释的情况下，我说一件事，该事情已被实际结果所证实。 集合均值的概率不等于同一集合中子集的概率的均值。 原始 Q-学习算法学习集合均值的概率。 但分布式 Q-训练针对每个分位数学习若干种方法。 然后我们找到这些概率值的平均值。

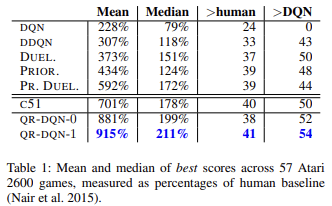
正如科学著作和实践所展现的那样，分位数回归通常受到各种异常值的影响较小。 这令模型训练过程更加稳定。 甚至，如此训练的结果乖离较小。 该方法的作者展示了训练模型工作基于 57 个 Atari 游戏的学习结果，并与其它算法训练的模型的成果进行了比较。 数据表明，平均结果几乎是原始 Q-学习（DQN）结果的 4 倍。 以下是原文章的结果表格 [6]

提高模型可用性，以前在创建测试所有强化学习模型的 EA 时，我们创建了各种方法，能根据训练模型的前馈结果选择操作。 创建的新类允许我们实现执行此功能的方法。 对于基于最大期望奖励的贪婪动作选择，我们来创建 getAction 方法。 它的算法非常简单。 我们仅调用上述 getResults 方法来获取前馈验算的结果。 从生成的缓冲区之中，我们选择拥有最高值的元素。

int CQRDQN::getAction(void)
  {
   CBufferFloat *temp;
   getResults(temp);
   if(!temp)
      return -1;
//---
   return temp.Maximum(0, temp.Total());
  }

我们不会实现 ɛ-贪婪动作选择策略，因为它用于旨在提高环境学习度的模型训练过程之中。 由于我们的奖励政策，没有必要采用这些方法。 在学习过程中，我们为所有可能的代理者动作提供目标。 

第二个 getSample 方法从概率分布中随机选择一个动作，其中较大的奖励具有更高的概率。 为了消除矩阵和数据缓冲区之间不必要的数据复制，我们部分地复用 getResults 方法的算法。

int CQRDQN::getSample(void)
  {
   CBufferFloat* resultVals;
   CNet::getResults(resultVals);
   if(!resultVals)
      return -1;
   vectorf temp;
   if(!resultVals.GetData(temp))
     {
      delete resultVals;
      return -1;
     }
   delete resultVals;
   matrixf q;
   if(!q.Init(1, temp.Size()) || !q.Row(temp, 0) || !q.Reshape(iActions, iNumbers))
     {
      delete resultVals;
      return -1;
     }

之后，我们调用 SoftMax 函数对前馈验算的结果进行归一化。 这些是动作选择概率。

   if(!q.Mean(1).Activation(temp, AF_SOFTMAX))
      return -1;
   temp = temp.CumSum();

我们收集累积概率总数的向量，并从生成的概率分布向量中实现采样。

   int err_code;
   float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code);
   if(random >= 1)
      return (int)temp.Size() - 1;
   for(int i = 0; i < (int)temp.Size(); i++)
      if(random <= temp[i] && temp[i] > 0)
         return i;
//---
   return -1;
  }

将采样结果返回至调用者程序。

我们已经研究了前馈和后馈方法，以及获得模型结果的方法。 但仍有许多悬而未决的问题。 其中之一是模型更新方法 Target Net — UpdateTarget。 我们在讨论反向传播方法时提到过这个方法。 尽管此方法是从另一个类方法调用的，但我决定将其公开，并授予用户对它的访问权限。 诚然，我们消除了从用户端控制目标网络状态的需要。 然而，我们不限制选择的自由。 如有必要，用户可以控制一切。

该方法算法非常简单。 我们先简单地调用当前对象的 save 方法。 然后，我们将数据恢复方法称为 Target Net。 对于每个操作，我们都要控制执行过程。 一旦成功更新 Target Net 之后，重置向后迭代计数器。 

bool CQRDQN::UpdateTarget(string file_name)
  {
   if(!Save(file_name, 0, false))
      return false;
   float error, undefine, forecast;
   datetime time;
   if(!cTargetNet.Load(file_name, error, undefine, forecast, time, false))
      return false;
   iCountBackProp = 0;
//---
   return true;
  }

注意对象类的差别。 我们在新的 CQRDQN 类中进行操作，而 Target Net 是父类 CNet 的一个实例。 关键点在于我们只调用来自 Target Net 的前馈功能。 此方法在我们的类中尚未修改。 因此，使用父类应该没有问题。 与此同时，当使用 CQRDQN 类的实例时，对于 Target Net，将递归创建新实例的内部 Target Net 对象。 这种反复出现的过程可能会导致严重错误。 因此，由这样一个微不足道的细节可能会对整个程序的运行产生重大影响。

我们已经研究了新 CQRDQN 类的主要功能，该类在分布式 Q-学习（QR-DQN） 中实现了分位数回归算法。 该方法发表于 2017 年 10 月的文献“使用分位数回归的分布强化学习”。

该类还实现了保存模型 — Save；和随后的还原 — Load。 这些方法的变化并不太复杂。 您可以在文后附带的代码中研究它们。 现在我建议继续测试新类。

3. 测试

我们通过训练模型来开始测试新类。 已为此创建了一个特殊的 EA，QRDQN-learning.mq5 来训练模型。 EA 是基于原始的 Q-学习 Q-learning.mq5 EA 创建的。 在此 EA 中，我们修改了要训练的模型类，并删除了目标网络模型实例声明。

CSymbolInfo          Symb;
MqlRates             Rates[];
CQRDQN               StudyNet;
CBufferFloat        *TempData;
CiRSI                RSI;
CiCCI                CCI;
CiATR                ATR;
CiMACD               MACD;

在 EA 初始化方法中，从先前创建的文件加载模型。 强制开启所有神经层的学习模式。 定义欲分析历史记录的深度，应与源数据层大小相等。 在模型中输入允许操作区域的大小。 还要指定目标网络的更新周期。 在这种情况下，我故意指示了一个高估的数值，因为我计划自己管理模型更新过程。

int OnInit()
  {
//---
.........
.........
//---
   if(!StudyNet.Load(FileName + ".nnw", dtStudied, false))
      return INIT_FAILED;
   if(!StudyNet.TrainMode(true))
      return INIT_FAILED;
//---
   if(!StudyNet.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   if(!StudyNet.SetActions(Actions))
      return INIT_PARAMETERS_INCORRECT;
   StudyNet.SetUpdateTarget(1000000);
//---
........
//---
   return(INIT_SUCCEEDED);
  }

训练模型的过程直接在 Train 函数中执行。

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

在函数中，我们定义训练周期并，加载历史数据。 这个过程完全保留了其原始形式。

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

接下来，我们为模型训练过程实现一个嵌套循环系统。 外部循环倒计时用于更新目标网络模型的训练周期。

   int total = bars - (int)HistoryBars - 240;
   bool use_target = false;
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int i = 0;
      uint ticks = GetTickCount();
      int count = 0;
      int total_max = 0;

在嵌套循环中，我们迭代前馈和后馈验算。 在此，我们首先准备历史数据，以便描述系统的两种后续状态。 其一将用于我们正在训练的模型的前馈验算。 第二个将用于目标网络。

      for(int batch = 0; batch < (Batch * UpdateTarget); batch++)
        {
         i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * total + 240);
         State1.Clear();
         State2.Clear();
         int r = i + (int)HistoryBars;
         if(r > bars)
            continue;
         for(int b = 0; b < (int)HistoryBars; b++)
           {
            int bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE ||
               sign == EMPTY_VALUE)
               continue;
            //---
            if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) ||
               !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) ||
               !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               break;
              }
            if(!use_target)
               continue;
            //---
            bar_t --;
            open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            rsi = (float)RSI.Main(bar_t);
            cci = (float)CCI.Main(bar_t);
            atr = (float)ATR.Main(bar_t);
            macd = (float)MACD.Main(bar_t);
            sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE ||
               sign == EMPTY_VALUE)
               continue;
            //---
            if(!State2.Add((float)Rates[bar_t].close - open) || !State2.Add((float)Rates[bar_t].high - open) || 
               !State2.Add((float)Rates[bar_t].low - open) || !State2.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State2.Add(sTime.hour) || !State2.Add(sTime.day_of_week) || !State2.Add(sTime.mon) ||
               !State2.Add(rsi) || !State2.Add(cci) || !State2.Add(atr) || !State2.Add(macd) || !State2.Add(sign))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               break;
              }
           }

实现我们正在训练的模型前馈。

         if(IsStopped())
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }
         if(State1.Total() < (int)HistoryBars * 12 ||
            (use_target && State2.Total() < (int)HistoryBars * 12))
            continue;
         if(!StudyNet.feedForward(GetPointer(State1), 12, true))
            return;

之后，为代理者的所有可能动作生成批量奖励，并调用主模型的向后馈送方法。

         Rewards.BufferInit(Actions, 0);
         double reward = Rates[i].close - Rates[i].open;
         if(reward >= 0)
           {
            if(!Rewards.Update(0, (float)(2 * reward)))
               return;
            if(!Rewards.Update(1, (float)(-5 * reward)))
               return;
            if(!Rewards.Update(2, (float) - reward))
               return;
           }
         else
           {
            if(!Rewards.Update(0, (float)(5 * reward)))
               return;
            if(!Rewards.Update(1, (float)(-2 * reward)))
               return;
            if(!Rewards.Update(2, (float)reward))
               return;
           }

请注意，根据覆盖的向后馈送方法，我们在该方法中不仅输入奖励缓冲区，还输入随后的当前状态。 我们还删除了目标网络操作模块，并根据未来状态的预期收入调整了奖励。

         if(!StudyNet.backProp(GetPointer(Rewards), DiscountFactor, (use_target ? GetPointer(State2) : NULL), 12, true))
            return;

在品种图表上输出有关处理进度的信息。

         if(GetTickCount() - ticks > 500)
           {
            Comment(StringFormat("%.2f%%", batch * 100.0 / (double)(Batch * UpdateTarget)));
            ticks = GetTickCount();
           }
        }

嵌套循环操作至此完毕。 及其所有迭代，检查当前模型错误。 如果先前实现的结果已得到改进，请保存当前模型状态并更新目标网络。 

      if(StudyNet.getRecentAverageError() <= min_loss)
        {
         if(!StudyNet.UpdateTarget(FileName + ".nnw"))
            continue;
         use_target = true;
         min_loss = StudyNet.getRecentAverageError();
        }
      PrintFormat("Iteration %d, loss %.8f", iter, StudyNet.getRecentAverageError());
     }
   Comment("");
//---
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   ExpertRemove();
  }

外部循环和整个学习函数的操作至此完毕。 EA 代码的其余部分没有改变。 附件中提供了所有类和程序的完整代码。

利用 NetCreator 工具创建了一个训练模型。 模型的体系结构与来自上一篇文章中训练模型的体系结构相同。 我删除了最后一个 SoftMax 规范化层，以便模型结果区域可以复制所用奖励策略的任何结果。

与以前一样，该模型是基于 EURUSD 历史数据、H1 时间帧上进行训练的。 训练数据集采用过去 2 年的历史数据。

训练模型的工作是在策略测试器中进行测试。 为测试目的创建了一个单独的 EA QRDQN-learning-test.mq。 该 EA 也是在之前文章中的类似 EA 的基础上创建的。 其代码没有太大变化。 附件中提供了其完整代码。

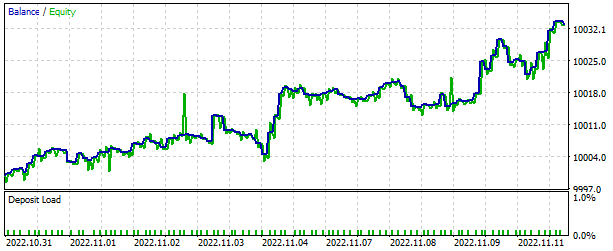
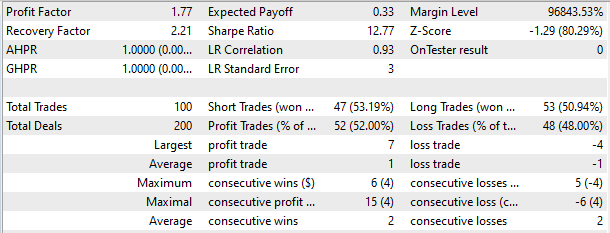
在策略测试器中，该模型展示了在 2 周的短期内产生盈利的能力。 超过一半的交易以盈利平仓。 每笔交易的平均盈利几乎是平均亏损的两倍。

结束语

在本文中，我们领略了另一种强化学习方法。 我们还创建了一个实现这些方法的类。 我们已经训练了模型，并在策略测试器中查看了其操作结果。 基于获得的结果，我们可以得出结论，在分布式 Q-学习中使用分位数回归算法，能实现解决真实市场问题的模型。

再一次，我想提请您注意这样一个事实，即本文中所介绍的所有程序仅用于技术演示目的。 模型和 EA 都需要进一步改进，以及全面的测试，然后才能用于真实交易。

参考

1. 神经网络变得轻松（第二十六部分）：强化学习
2. 神经网络变得轻松（第二十七部分）：深度 Q-学习（DQN）
3. 神经网络变得轻松（第二十八部分）：政策梯度算法
4. 神经网络变得轻松（第三十二部分）：分布式 Q-学习
5. 强化学习之上的分布视角
6. 使用分位数回归的分布强化学习

本文中用到的程序

#	发行	类型	说明
1	QRDQN-learning.mq5	EA	优化模型的 EA
2	QRDQN-learning-test.mq5	EA	在策略测试器中测试模型的智能系统
3	QRDQN.mqh	类库	QR-DQN 模型类
4	NeuroNet.mqh	类库	创建神经网络模型的类库
5	NeuroNet.cl	代码库	创建神经网络模型的 OpenCL 程序代码库
6	NetCreator.mq5	EA	模型构建工具
7	NetCreatotPanel.mqh	类库	创建工具的类库