Популяционные алгоритмы оптимизации: Устойчивость к застреванию в локальных экстремумах (Часть I)

Содержание:

1. Введение
2. Постановка задачи
3. Код, необходимые изменения
4. Обсуждение алгоритмов
5. Предварительные выводы

1. Введение

Это уникальное исследование, идея которого появилась у меня во время ответов на вопросы, возникших в ходе обсуждения одной из моих статей. Я полон надежды, что читатели смогут оценить ценность и оригинальность этой работы.

Мои мысли и идеи, приведшие к этому исследованию, являются результатом глубокого погружения в тему и страсти к научному исследованию и я верю, что эта работа может стать важным вкладом в область алгоритмической оптимизации, привлекая внимание исследователей и практиков.

В данном эксперименте предлагаю провести тест, направленный на оценку устойчивости алгоритмов к застреванию в локальных экстремумах и вместо случайного размещения агентов на первой итерации по всему полю пространства поиска — разместить их в глобальном минимуме. Задачей эксперимента является поиск глобального максимума.

В таком сценарии, где все поисковые агенты алгоритма размещены в одной точке, мы сталкиваемся с интересным феноменом – вырожденной популяцией. Это подобно моменту замирания времени, где разнообразие в популяции сведено к минимуму. Хотя такой сценарий является искусственным, он позволяет получить интересные выводы и оценить влияние сокращения разнообразия в популяции на результат. Алгоритм должен быть способен выбраться из такого "бутылочного горлышка" и достичь глобального максимума.

В этом своеобразном стресс-тесте для алгоритмов оптимизации мы можем раскрыть тайны взаимодействия агентов, их кооперации или конкуренции, и понять, как эти факторы влияют на скорость достижения оптимума. Такой анализ открывает новые горизонты в понимании важности разнообразия в популяции для эффективной работы алгоритмов и позволяет выработать стратегии поддержания этого разнообразия для достижения лучших результатов.

Для проведения эксперимента нужно предварительно инициализировать координаты агентов принудительно снаружи по отношению к алгоритму, используя координаты глобального минимума, перед тем как измерить функцию приспособленности на первой эпохе.

Такой эксперимент позволит оценить устойчивость к крайне сложным условиям, и способность преодолевать ограничения.

2. Постановка задачи

Представьте себе, что вы находитесь в глубокой впадине долины, окруженной плотным мраком. Ваши глаза завязаны, лишив вас возможности видеть окружающий мир. Вы ощущаете холодный ветер, который пронизывает ваше лицо и ваше сердце бьется сильно, словно пытается вырваться из груди, подчеркивая вашу тревогу и неопределенность.

Вы начинаете двигаться, сделав первый шаг вперед. Ваши ноги ощущают землю, и вы постепенно перемещаетесь по впадине, с каждым шагом приближаясь к свободе и ваше сознание наполняется решимостью. И наконец, когда вы достигаете края, перед вами открывается захватывающий вид. Ровная как стекло равнина простирается перед вами, словно бескрайнее полотно, одиночные крутые скалы, которые возвышаются вдали, вызывают смешанные чувства изумления и испытываемого вызова. Однако, несмотря на эту прекрасную панораму, вам все еще не доступно это увидеть.

Вы решаете полагаться на свои ощущения и интуицию, чтобы определить направление, в котором нужно двигаться и достичь вершины самой высокой скалы. Теперь представьте, что перед этой непростой задачей стоит алгоритм на тестовой дискретной функции Megacity. Этот алгоритм, как и вы, ограничен своими возможностями и не может видеть или ощущать окружающую среду напрямую. Он должен использовать свои вычислительные способности и логику, чтобы принять решение о наилучшем пути к вершине самой высокой скалы. Таким образом, эта задача на тестовой дискретной функции Megacity является сложным вызовом для алгоритма, который, подобно вам, стоит перед трудностями и неопределенностью.

Впрочем, функции Hilly и Forest также представляют собой непростую задачу в подобной постановке. Давайте взглянем со стороны на эти знакомые нам функции, чтобы оценить сложность предстоящей задачи для алгоритмов.

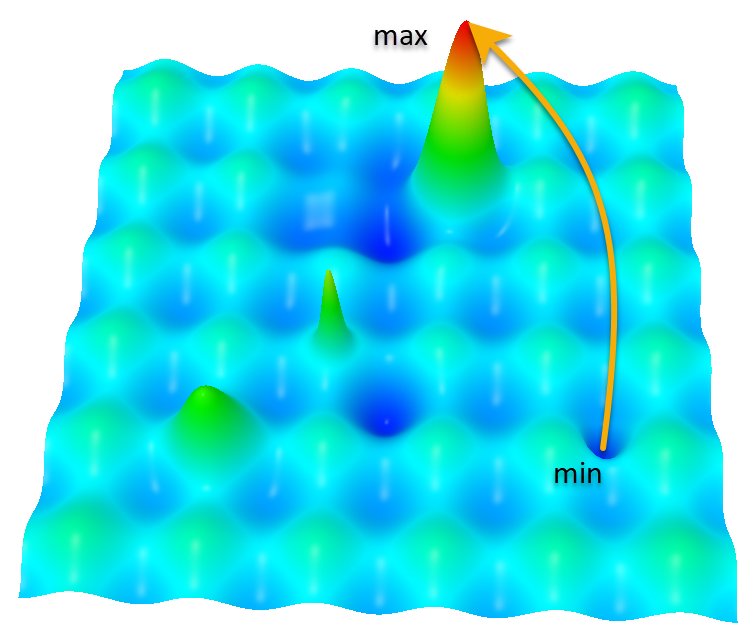
Функция Hilly

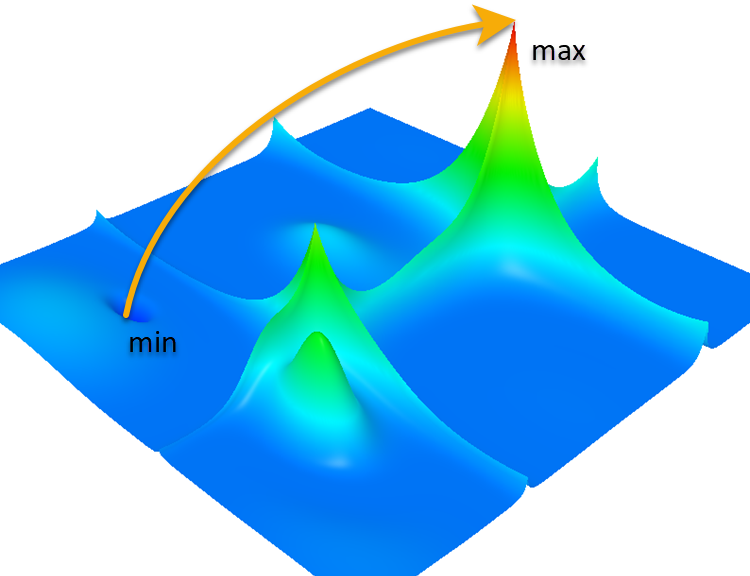
Функция Forest

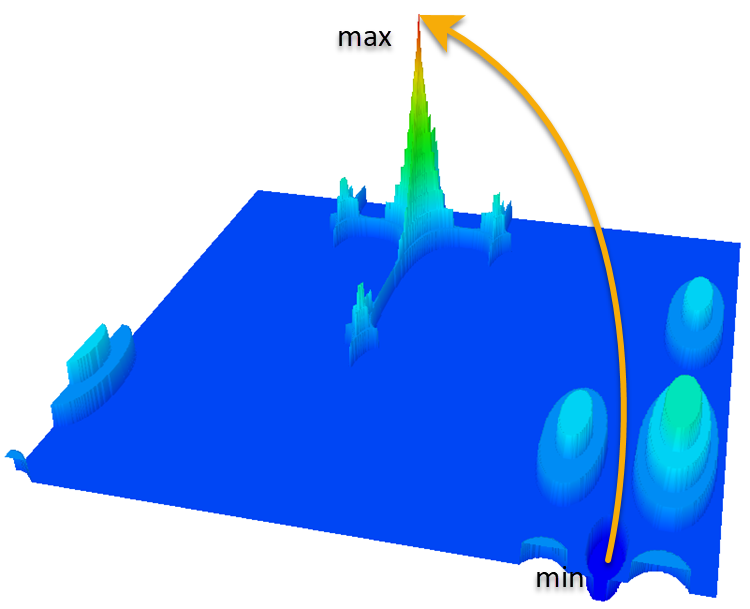
Функция Megacity

Представьте себе, что вы — алгоритм, воплощение вычислительной мощи и логического мышления. Вы не просто сухие строки кода или формулы на бумаге, вы оживаете и берете на себя роль исследователя. Ваш разум наполняется вопросами и гипотезами, и вы стремитесь разгадать загадку, которая стоит перед вами. Вы погружаетесь в мир данных и информации, анализируете, сравниваете и выделяете ключевые факторы, а ваши вычислительные способности работают на полную мощность. Вы начинаете строить различные модели и сценарии, исследуя возможные пути к решению задачи и пробуете разные комбинации и варианты, и ваше творчество приводит к новым открытиям. Но путь к решению не всегда прост. Вы сталкиваетесь с вызовами и сложностями, которые могут показаться непреодолимыми, но не сдаетесь. Вы преодолеваете преграды и ловушки, отвлекающие внимание, одну за другой, с каждым шагом приближаясь к своей цели. И наконец, когда вы находите решение, это подобно мгновению просветления. Ваш разум озаряется ярким светом понимания, и вы видите, как все элементы встают на свои места. Представили?

В контексте данной картины, алгоритм оптимизации сталкивается с задачей максимизации функции, которая имеет сложную топологию с множеством локальных максимумов. Вот более подробное описание проблемы:

• Локальные максимумы. На пути от начальной точки (отмечено как "min") к конечной точке (отмечено как "max") алгоритм сталкивается с множеством локальных максимумов. Это может привести к тому, что алгоритм "застрянет" в локальной ловушке, не достигнув глобального экстремума. Это является основной проблемой в задачах оптимизации, например, для алгоритмов, основанных на градиентном спуске, они обычно "поднимаются" к ближайшему максимуму, и если это локальный максимум, тогда "застревают".

• Высокая размерность. Если мы рассматриваем функцию в многомерном пространстве, то количество локальных максимумов резко увеличивается, что усложняет задачу. В высоких размерностях пространство становится "пустым", что делает задачу еще более сложной из-за того, что алгоритму не за что зацепиться.
  

• Сложность поверхности функции. Поверхность функции может быть очень сложной с большим количеством пиков и впадин, что делает процесс оптимизации более трудоемким. Это требует от алгоритма способности перепрыгивать через локальные максимумы и подниматься к глобальному максимуму. 

• Сходимость и скорость сходимости. Сходимость алгоритма к максимуму функции может быть замедлена из-за дальности точки финиша от точки старта, что может потребовать дополнительных итераций для достижения цели.

• Исследование области. Алгоритму может потребоваться дополнительное исследование области в поисках глобального максимума, что может привести к увеличению вычислительной сложности.

Подводя итог описанию проблемы, можно выделить разницу между типичной ситуацией оптимизации, где агенты начинают своё движение в пространстве поиска равномерно распределенными, и ситуацией, где необходимо не просто "выявить" уже имеющуюся информацию, а скорее исследовать и расширять свои знания и опыт в неизведанные участки пространства. Такая формулировка задачи становится особенно ценной в тех случаях, когда у нас уже имеются некоторые решения, полученные в предшествующих сессиях оптимизации, и мы стремимся начать именно с этой "точки" решения, вместо того чтобы просто кристаллизовать имеющуюся информацию.

3. Код, необходимые изменения

Для того, чтобы разместить агентов в одной точке, присвоим соответствующим координатам агентов популяции координаты глобального минимума тестовой функции. В общем виде эта процедура будет выглядеть следующим образом:

if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].c [i * 2]     = f.GetMinFuncX ();
      AO.a [set].c [i * 2 + 1] = f.GetMinFuncY ();
    }
  }
}

Для некоторых алгоритмов недостаточно просто разместить агентов в одной точке пространства поиска — требуется внесение дополнительной информации. Например, в случае алгоритма SDSm необходимо также указать соответствующий сектор для каждой координаты. С другой стороны, при использовании алгоритма BGA необходимо преобразовать значения координат из вещественного представления в бинарное, что влечет за собой дополнительные изменения в коде алгоритма. Для BGA расположение агентов в одной точке будет выглядеть следующим образом:

//==================
if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].DoubleToGene (f.GetMinFuncX (), i * 2);
      AO.a [set].DoubleToGene (f.GetMinFuncY (), i * 2 + 1);
    }

    AO.a [set].ExtractGenes ();
  }
}
//==================

Как видно из данного кода, здесь происходит необходимое преобразование координат в двоичный код генов. В настоящее время я работаю над унификацией процесса размещения агентов в нужных координатах. В данном исследовании представлены исходные коды в их текущем состоянии. Почти для каждого алгоритма требовался индивидуальный тестовый стенд из-за особенностей их архитектуры. Следите за публикациями новых статей, чтобы получить обновления по алгоритмам. Упрощение процесса размещения координат в популяции и их унификация будут осуществлены и приведены к общему стандарту.

4. Обсуждение алгоритмов

Переходя к анализу поведения алгоритмов в рамках нашего уникального тестирования, мы приступаем к обсуждению алгоритмов, которые продемонстрировали наихудшие результаты. Особенно удивительным является то, что некоторые из них, ранее занимавшие достаточно высокие позиции в рейтинге при стандартных тестах, показали себя неудовлетворительно в нашем необычном испытании. Это наводит на мысль о том, что успешность алгоритмов может зависеть не только от их общей эффективности, но также от их способности адаптироваться к конкретным условиям и особенностям задачи. Такие неожиданные результаты подчеркивают важность проведения разнообразных тестов и исследований для получения более глубокого понимания работы алгоритмов оптимизации в различных контекстах.

Далее будут приведены отчеты работы алгоритмов, которые нужно читать так:

• C_AO_FSS:50;0.01;0.8             - название алгоритма и его внешние параметры
  
• 5 Hilly's                                   - название тестовой функции и её количество в тесте
  
•  Func runs: 10000                   - количество запусков
  
• result: 0.32457068874346456  - полученный результат, где 0.0 - минимум тестовой функции, а 1.0 - максимум,  чем больше значение, тем лучше
  
• All score: 1.33084                   - общее значение набранных баллов, чем больше значение, тем лучше
  

Дифференциальная эволюция, DE

К сожалению, даже один из самых мощных алгоритмов в рейтинговой таблице полностью провалил наше тестирование. В этом случае агенты оказались в застое, не смещаясь с места. Причина этого провала заключается в том, что каждое новое положение агента зависит от позиций трех других агентов, и если все они оказываются в одной точке, то ни один из них не сможет обновить свои координаты. Эта ситуация подчеркивает важность тщательного анализа взаимодействия между агентами и адекватного управления их перемещениями для успешного выполнения задачи оптимизации. Такие неожиданные сбои могут послужить стимулом для дальнейших исследований и улучшений в разработке алгоритмов, способных эффективно справляться с подобными сложностями.

Для других алгоритмов, полностью  проваливших тест, я не буду приводить распечатку тестового стенда.

Алгоритм электромагнитного поиска, EM

Алгоритм EM столкнулся с проблемой невозможности обновления координат агентов в процессе оптимизации. В данном случае наблюдалось схлопывание частиц под воздействием электромагнитного притяжения, что привело к тому, что агенты объединились в один комок.

Алгоритм гравитационного поиска, GSA

Силы гравитации привели к тому, что все объекты как были в одной точке, так и остались там - они притянуты в центр, аналогично черной дыре.

Алгоритм искусственной муравьиной колонии, ACOm

У этого алгоритма проблемой стало отсутствие дорожек для передвижения муравьев, которые бы двигались, руководствуясь запахами феромонов. В данном случае, поскольку муравьи стартовали из одной точки, дорожки между ними не были сформированы, что привело к затруднениям в передвижении и координации действий муравьев.

Поиск косяком рыб, FSS

В данном алгоритме рыбы используют разницу в приспособленности между последней и предыдущей итерациями для определения своего направления движения. В то время как на функциях Hilly и Forest рыбы чувствуют изменения ландшафта, запуск алгоритма на ровной поверхности Megacity вводит рыб в замешательство, лишая их ориентации. Удивительное поведение рыб проявляется при старте на гладких поверхностях, имеющих градиент. Однако, если начальная точка находится на вершине локального экстремума, а не в яме, даже на функциях Hilly и Forest рыбы вряд ли будут двигаться.

Имитация изотропного отжига, SIA

Алгоритм имитации изотропного отжига демонстрирует уникальное сочетание черт, напоминающих работу FSS, но с существенными отличиями. В этом алгоритме движение в разные стороны от исходной точки происходит более энергично и активно, чем в FSS, создавая ощущение бурного творчества в поиске оптимального решения. Подобно FSS, алгоритм симуляции изотропного отжига использует различия в значениях фитнес-функции для направления движения. Однако здесь движение подвержено влиянию постепенного снижения температуры, что со временем приводит к "замораживанию" частиц в определенных точках пространства.

Эволюционные стратегии, (PO)ES

Этот алгоритм оказался первым в списке, который смог успешно завершить все тесты. Хотя использование термина "успешно завершил" кажется категоричным, на самом деле он прошел каждый из них, хотя бы с каким-то результатом, отличным от нулевого. Замечательно, что в процессе наблюдается стремление популяции к разделению на отдельные группы. Однако, начального энтузиазма алгоритму хватает лишь на короткое время - агенты быстро прекращают поиск на первой ближайшей возвышенности, вероятно, предполагая, что они уже добились успеха.

Особенно занимательно, что в начале агенты, разделившись на группы, внушают оптимизм наблюдателю, двигаясь в разных направлениях, но разочарование приходит быстро: как только одна из групп достигает заметного улучшения положения, все остальные группы моментально меняют направление, устремляясь к лидеру. Эти мгновения вызывают смешанные чувства и эмоции - от восторга до разочарования. Взаимодействие агентов в этом алгоритме напоминает жизнь со всеми ее неожиданностями и переменчивостью.

Алгоритм обезьян, MA

В контексте этого алгоритма обезьяны продолжают двигаться в выбранном направлении довольно изолированно, даже если это направление оказывается неверным. Это уникальное поведение позволяет агентам исследовать пространство более эффективно, распространяясь дальше от исходной точки. Они осуществляют далекие "прыжки в неизвестность", особенно впечатляющие на дискретной функции Megacity, где отсутствует приращение приспособленности на горизонтальных поверхностях, что способствует достижению отдаленных областей.

Однако, несмотря на эту способность к исследованию, она оказывается недостаточной для достижения основной цели, поскольку количество доступных итераций подходит к концу. Важно отметить увлекательное визуальное поведение алгоритма, которое по-настоящему напоминает хаотичное движение обезьян в стае, создавая удивительное зрелище и вызывая интерес к его дальнейшему исследованию и совершенствованию.

Имитация отжига, SA

В алгоритме имитации отжига, в отличие от своего "родственника" SIA, который, к слову, занимает гораздо более высокую позицию в рейтинге, поведение проявляется более хаотично, что даже заметно невооруженным глазом на визуализации. Эта хаотичная природа "отжигающей" имитации, однако, оказывает благоприятное воздействие, помогая достичь немного более лучших результатов. Хотя, конечно, эти достижения не настолько велики, чтобы увековечить этот алгоритм в зале славы выдающихся алгоритмов, но улучшение заметно и заслуживает признания.

Светлячковый алгоритм, FAm

FA - один из моих любимых алгоритмов. Его привлекательность проявляется не только в самом красивом названии, но и в изящной идее, лежащей в основе, а также в элегантном поведении светлячков. Эти мистические светящиеся создания способны мгновенно приближаться к ближайшим локальным экстремумам с такой скоростью, что за ними действительно трудно уследить. Однако, после этого великолепного шоу происходит застой, когда агенты оказываются застрявшими в локальных максимумах, лишены возможности исследовать пространство дальше и достичь глобального оптимума.

Этот момент застоя, хотя и может показаться разочарованием, открывает возможность для улучшения алгоритма. Путем внедрения механизмов, способствующих преодолению локальных ловушек, FA может обрести новые горизонты эффективности и точности. Таким образом, даже в моменты, когда светлячки останавливаются, мы видим не просто конец, а новое начало - возможность совершенствования и развития этого удивительного алгоритма.

Алгоритм оптимизации бактериального поиска пищи, BFO

Способность бактерий сохранять свою подвижность даже без необходимости повышать свою приспособленность является ключевым фактором, позволяющим им эффективно распространяться на большие расстояния, превосходя в этом аспекте рассмотренные выше алгоритмы. Этот удивительный феномен проявляется особенно ярко в условиях Megacity, где бактерии демонстрируют удивительную способность к мобильности и выживаемости, позволяя им успешно адаптироваться к разнообразным и сложным окружающим условиям. В этом контексте бактерии становятся настоящими пионерами, исследующими и колонизирующими новые территории, что подчеркивает их уникальные возможности и значимость в мире живых организмов.

Алгоритм поиска системой зарядов, CSS

Удивительно, но этот алгоритм в данном тестировании проявил себя совершенно неожиданно, превзойдя свои обычные показатели, где он занимает предпоследнее место среди аутсайдеров рейтинга. На этот раз CSS удивил всех, заняв где-то посередине (двенадцатое снизу) место. Тайна этого превращения имеет свое объяснение: электростатические заряды, подчиняющиеся формулам алгоритма, начинают взаимодействовать с силами отталкивания при попадании в пределы радиуса заряда, что позволяет им взрывообразно распространяться в окружающем поисковом пространстве. Этот процесс не только визуально привлекателен, но и обладает потенциалом для практического применения.

Эта способность, выстреливать как хлопушка, CSS открывает новые возможности использования. Например, можно рассматривать этот алгоритм как источник "идей"-решений для определения оптимального положения агентов для других алгоритмов оптимизации или успешно интегрировать его в гибридные решения, где CSS поможет избежать вырождения популяции. Таким образом, неожиданный успех CSS в этом тестировании не только вдохновляет, но и открывает новые перспективы для его применения.

Алгоритм растущих деревьев, SSG

Данный алгоритм раскрывает свой потенциал на функциях с градиентом, таких как Hilly или Forest, и занимает высокие позиции в стандартном рейтинге. Однако его эффективность проявляется в полной мере лишь при наличии положительного изменения градиента. В противном случае популяция быстро деградирует, а индивиды сходятся в одной лучшей локальной точке, что открывает возможность применения метода SSG для уточнения результатов алгоритмов оптимизации.

5. Предварительные выводы

В этом уникальном исследовательском эксперименте, где алгоритмы были подвергнуты строгим начальным условиям, мы обнаружили множество увлекательных особенностей различных алгоритмов, которые остались скрытыми при стандартном случайном равномерном размещении агентов в пространстве поиска. Подобно тому, как это происходит в реальной жизни, организмы раскрывают свой внутренний потенциал в экстремальных условиях.

Мы также стали свидетелями неожиданных результатов испытаний некоторых алгоритмов, включая их падение с верхних позиций рейтинга на самый низ. Это позволяет нам лучше понять, как использовать алгоритмы в зависимости от их способностей в специализированных задачах оптимизации, а также более глубоко изучить их сильные и слабые стороны. Также это ярче выявило как положительные, так и отрицательные стороны каждого алгоритма, что позволяет более эффективно использовать их сильные стороны и компенсировать слабые. Кроме того, это исследование способствует лучшему пониманию создания гибридных алгоритмов, позволяя объединять сильные стороны различных методов для достижения оптимальных результатов.

В следующей статье мы продолжим рассмотрение свойств и поведения алгоритмов и подведем итоги.