
Угловые операции для трейдеров
Введение
Угловые операции в трейдинге используются очень давно. Основным достоинством этих операций является простота построения углов и их наглядность. Ярким примером угловых операций являются инструменты Ганна.
Казалось бы, все про углы уже известно. Но мы попробуем взглянуть на углы под другим углом (прощу прощения за тавтологию). И попытаемся вспомнить хорошо забытое старое, чтобы получить что-то совершенно новое.
Строим первый угол
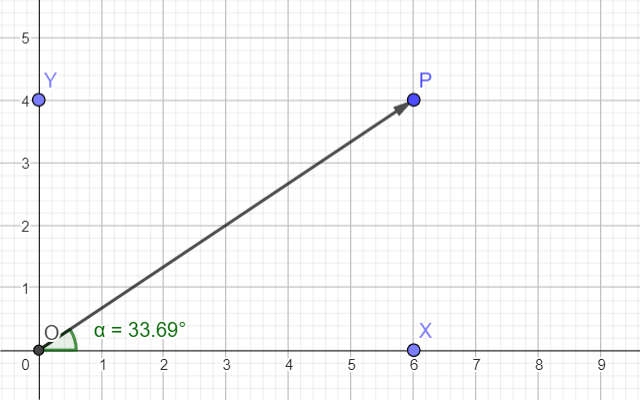
Угол – это одна из простейших геометрических фигур. Провести две линии из одной точки – что может быть проще? При этом одной из линий, чаще всего, служит ось абсцисс.
В этом случае величину угла очень просто рассчитать через координаты точки P.
Так как угол является безразмерной величиной, то по обеим осям должны быть одинаковые величины. Если по одной оси у вас отсчитываются метры, а по другой – килограммы, то вы получите какое-то соотношение между ними, но никак не угол.
Давайте попробуем воплотить угловую операцию в виде индикатора. Я буду делать такой индикатор: по осям X и Y будут отображаться цены разных валютных пар. Тогда небольшой по значению угол будет соответствовать большой цене первой валютной пары, и низкой цене для второй. Соответственно, большой угол будет говорить о том, что цена второго символа выше, чем первого. То есть, наш будущий индикатор будет определять перекупленность/перепроданность одной валютной пары относительно другой. Неплохая идея для парного трейдинга.
Первое затруднение, с которым мы сталкиваемся, по разным осям у нас разные величины (для примера я взял EURUSD и USDJPY). Это затруднение мы преодолеваем легко и просто – цену каждого инструмента мы поделим на величину пункта.
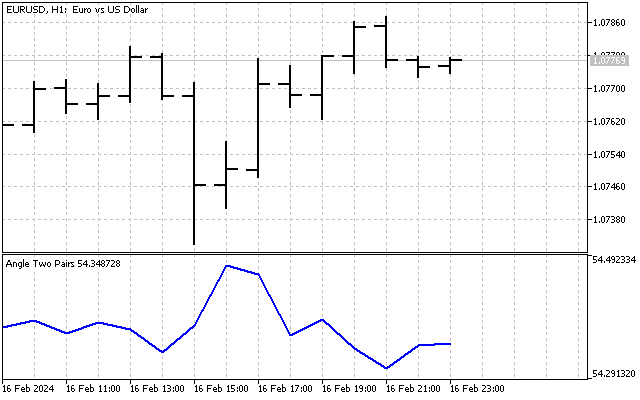
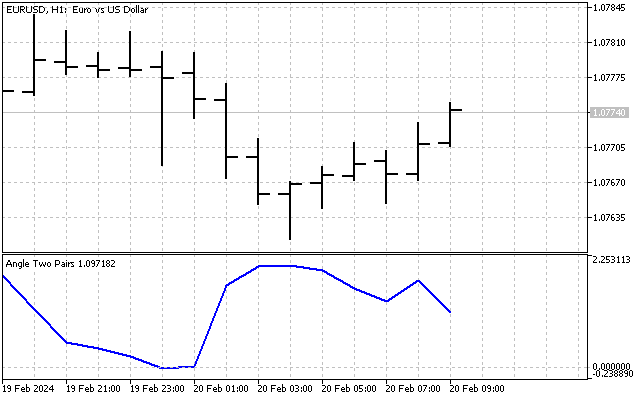
Тогда мы сразу решаем две проблемы – по обеим осям у нас будут сравнимые величины (цена, выраженная в пунктах), плюс масштаб по этим осям будет одинаков. А вот так выглядит наш индикатор.
На первый взгляд индикатор кажется довольно банальным. Его значение колеблется около какого-то среднего значения, а разность между максимумом и минимумом индикатора составляет всего-то 2-3 градуса. Но, давайте не будем делать преждевременных выводов. Возможно, мы сумеем улучшить этот индикатор и сделать его более информативным.
Небольшое напоминание. Наиболее распространенной угловой мерой, которую мы используем в обычной жизни, является градус. А для математических вычислений, чаще всего, используется радианная мера. Переход от градусной меры к радианной и наоборот, осуществляется по формулам:
Т.е., перевод градусов в радианы и обратно – это просто умножение на некоторый масштабирующий коэффициент. Однако, если вам нужно вывести информацию в числовом виде, то предпочтительнее использовать градусы. Согласитесь, что 45° выглядит лучше, чем 0.78539 rad. По сути одно и то же, но первое значение выглядит нагляднее.
Углы и нормальное распределение
При изучении реальных процессов исследователи используют различные распределения вероятностей случайных величин. Наиболее известным распределением является нормальное.
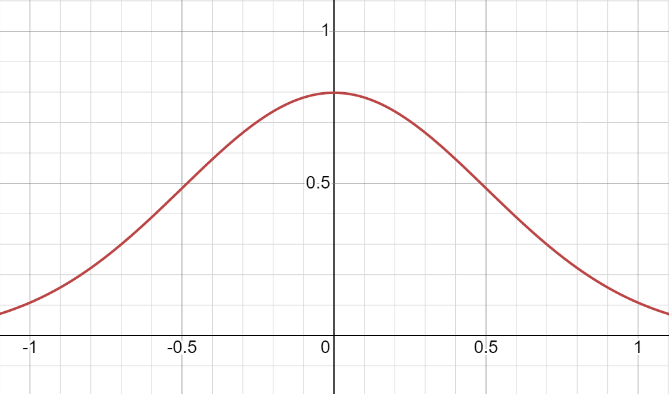
Давайте вспомним некоторые свойства нормального распределения. Его график представляет собой колоколообразную линию. А концы этой линии уходят в бесконечность.
Мысленно проделаем такую операцию. Мы начнем потихоньку сворачивать ось X в окружность. При этом, мы будем следовать такому правилу – чем дальше мы отойдем от центра, тем сильнее будет сворачивание. Если мы проявим терпение, то ось X превратится в окружность. Исказится и сама линия нормального распределения, и в результате у нас получится круговое нормальное распределение.
Первое отличие обычного нормального распределения от кругового заключается в том, что -∞ отображается в -180°, а +∞ в +180°. Но, не ради этого мы старались. Главное предназначение кругового нормального распределения – обработка угловых величин. Сама формула кругового нормального распределения выглядит так:
Как мы можем видеть, в круговом распределении используются и среднее, и среднеквадратическое отклонение. Все, как у обычного нормального распределения. Немного пугает суммирование, но при работе с реальными данными мы легко справимся с этими бесконечностями.
Давайте возьмем наш индикатор и применим к нему круговое нормальное распределение.
Сначала нам нужно определить среднее всех углов, встречающихся в истории. В нашем случае, найти среднее не составит большого труда – обычное суммирование и деление на количество наблюдений. Но, вообще говоря, угловое среднее нужно искать немного иначе. Представьте, что вам нужно найти среднее двух углов – 10° и 350°. Обычный подход дает ответ в 180°. И, этот ответ неправильный. Правильный ответ – их среднее равно нулю.
Чтобы получить правильный ответ в любой ситуации нам придется поступить следующим образом: сначала нам нужно найти суммы синусов и косинусов всех углов. Разделим первую сумму на вторую, и получим тангенс среднего угла.
Теперь, найти величину среднего угла не составит никакого труда. Но, и тут есть небольшое условие. Если все углы лежат в пределах от -90° до +90°, то можно использовать функцию MathArctan. Если углы выходят за эти пределы нужно обязательно использовать более универсальную функцию MathArctan2.
Таким образом, средний угол будет равен:
После того, как мы оценили значение среднего угла, можно приступать к оценке среднеквадратического отклонения. Для этого мы можем использовать метод Ямартино. Сначала нам нужно найти вспомогательную величину:
Она дает уже достаточно точную оценку стандартного отклонения, но и ее можно улучшить:
Теперь, давайте внесем изменения в наш индикатор. Его показания будем рассчитывать так: сначала найдем разность между текущим и средним углами, а потом сравним эту разность со среднеквадратическим отклонением. В результате у нас получится такая картинка.
Индикатор позволяет точнее определять уровни перекупленности/перепроданности, а его ближайшим аналогом является индикатор CCI.
Углы и линейная функция
С углами для однотипных данных мы с вами разобрались. А можно ли применить угловые операции к тренду? Ответ – нет, так как мы имеем дело с данными разных типов, по одной оси у нас время, а по другой – цена.
Что ж, ответ правильный, но неверный. Давайте вспомним о линейной функции. Она описывает линейную взаимосвязь между двумя независимыми переменными и задается уравнением:
Казалось бы, а где здесь угол? А угол скрывается в коэффициенте k. Этот коэффициент равен тангенсу угла наклона линии относительно оси X.
Давайте попробуем применить эту функцию для описания тренда. Уравнение линейной функции для трейдеров будет выглядеть так:
В этом случае коэффициент k получит еще одно толкование – он показывает среднее изменение цены за единицу времени. Еще одно маленькое примечание: я вписал в формулу время – это академично и правильно. Но, при реальных расчетах гораздо проще использовать вместо времени индексы. Во-первых, праздники и выходные дни очень сильно повлияют на точность расчетов. А во-вторых, использование индексов делает формулы (и вычисления) намного проще. Единственное требование к этим индексам – они должны возрастать слева направо.
Теперь давайте посмотрим на способы оценки параметров линейного тренда. В первую очередь мы можем использовать метод наименьших квадратов (МНК). Напомню, что я вместо времени использую индексы, значения которых изменяются от 0 до n-1.
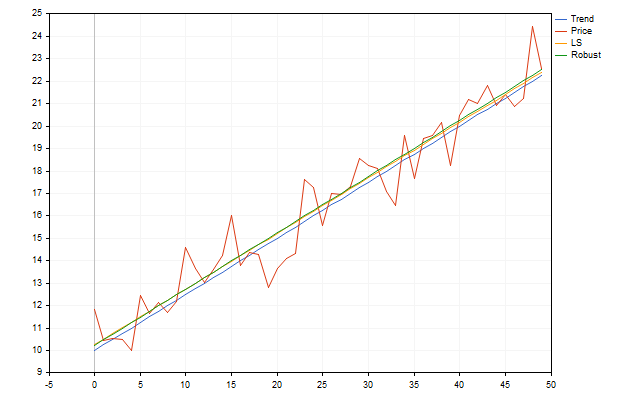
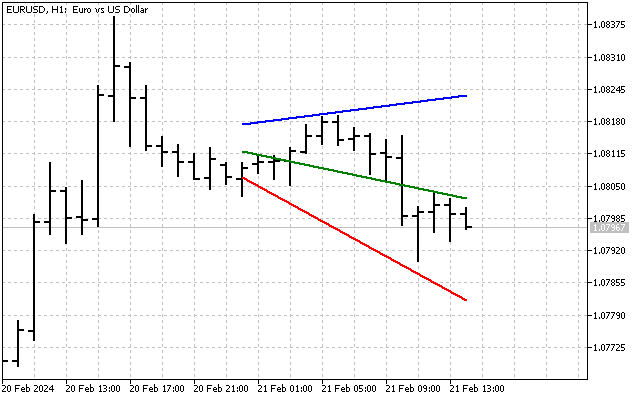
Но есть и более надежные способы для оценки этих параметров. Например, мы можем использовать оценку Тейла-Сена. Давайте посмотрим, как эта оценка может работать в реальных условиях. Возьмем тренд с параметрами k=0.25 и b=10. Добавим к нему немного шума, в виде случайно распределенных отклонений. По получившимся точкам попробуем найти параметры исходного тренда. В результате мы получим примерно такую картинку.
На первый взгляд кажется, что робастный метод не дает больших преимуществ. Но, это только потому, что ошибки в нашей модели тренда были распределены одинаково и по нормальному закону. Реальные цены могут не соответствовать этому критерию. Тогда метод Тейла-Сена будет работать намного лучше, к тому же он может дать немного больше информации. Именно робастную оценку я буду использовать в дальнейшем.
Итак, давайте рассмотрим, как можно оценить параметры линейного тренда с помощью метода Тейла-Сена. Сначала нам нужно найти параметр k. Он будет равен медиане из всех возможных разностей вида:
Значение медианы можно найти следующим образом. Сначала записываем все значения в массив. Потом сортируем его. Медиана будет равна значению, находящемуся в центре массива.
Теперь мы можем приступать к оценке параметра b. Для этого нам нужно найти медиану от всех возможных значений:
С теорией мы разобрались, пора переходить к практике. Давайте посмотрим, какие возможности открывает нам использование оценки Тейла-Сена.
Оценка Тейла-Сена и индикаторы
После оценки параметров тренда, у нас осталось два массива с данными. Давайте посмотрим, можем ли мы использовать эти массивы как-то еще.
Итак, мы оценили параметры тренда, и даже построили его линию. Теперь мы можем построить канал, внутри которого происходит движение цены. Для этого нам нужно сначала оценить, насколько сильно отклоняются цены от трендовой линии.
Возьмем массив, с помощью которого мы оценивали значение параметра b. Для того, чтобы оценить отклонение нам нужно найти медиану абсолютного отклонения. Т.е., сначала для каждого элемента массива находим абсолютное значение разности с параметром b. После чего остается найти медиану из полученных значений. Эта медиана даст робастную оценку стандартного отклонения.
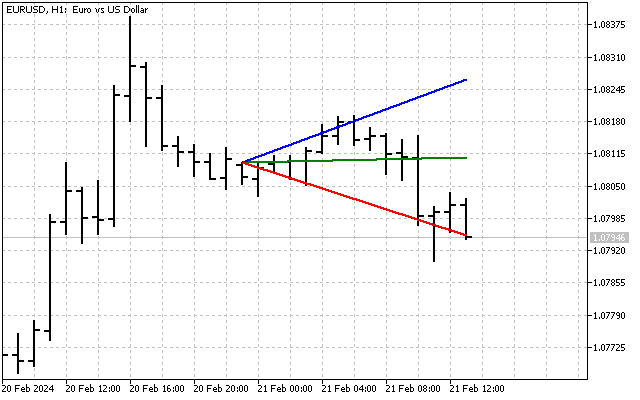
Зная стандартное отклонение, мы можем построить трендовый канал. Например, так выглядит канал шириной в 6 стандартных отклонений.
Этот индикатор по своей сути похож на Bollinger Bands. Кроме того, линии трендового канала можно использовать в качестве линий поддержки и сопротивления.
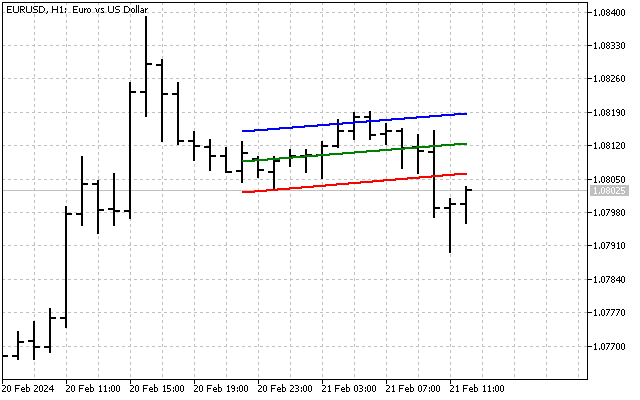
Кроме того, мы можем построить веер трендовых линий. Все вычисления производятся так же, как и при построении канала. Единственное отличие – нужно взять параметр k и соответствующий массив. Вот так выглядит веер с размахом в 1 отклонение по углу.
Ну, и конечно же, мы можем совместить канал и веер. Для этого сначала мы строим линии канала. А потом применяем к этим линиям веер. В результате мы получим примерно такую картинку.
Итак, применение робастных методов позволило нам получить линию тренда, и еще три дополнительных индикатора, которые можно использовать в техническом анализе.
Еще несколько слов
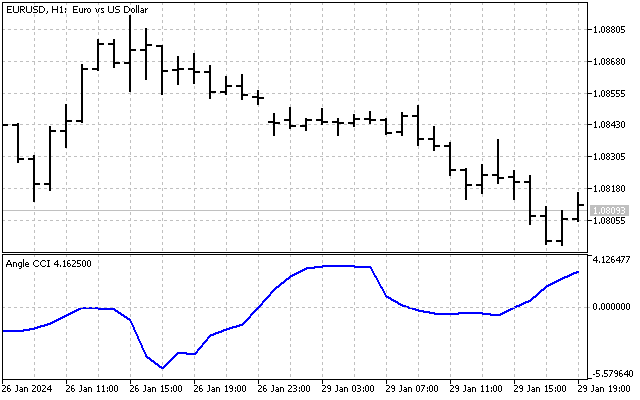
Угловые операции можно применять не только для построения трендов и углов. Возьмем, уже упоминавшийся в статье индикатор CCI. А что будет, если мы сделаем аналогичный индикатор. Но, в качестве исходных данных, мы будем использовать не цены, а углы тренда.
Тогда, мы сможем оценивать изменения тренда по истории. А вот так будет выглядеть наш индикатор.
Все технические индикаторы можно переделать под работу с угловыми величинами. С такими переделками вы можете открыть для себя новые способы технического анализа.
Заключение
При написании статьи были использованы следующие программы.
| Название | Тип | Описание |
|---|---|---|
| Angle Two Pairs | Индикатор |
|
| LS vs Robust | Скрипт | Сравнивает работу МНК и оценку Тейла-Сена |
| Theil–Sen estimator | Индикатор |
|
| Angle CCI | Индикатор |
|
 Работаем с датами и временем в MQL5
Работаем с датами и временем в MQL5
 Оптимизация и тестирование торговых стратегий (Часть 1): Взгляд на "Red Dragon H4", "BOLT", "YinYang", и "Statistics SAR"
Оптимизация и тестирование торговых стратегий (Часть 1): Взгляд на "Red Dragon H4", "BOLT", "YinYang", и "Statistics SAR"
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
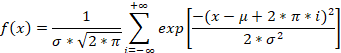
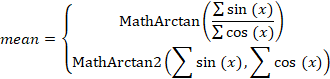
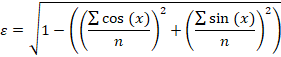
у меня от углов Ганна аж в глазах зарябило)
Во-первых, я не буду рисовать вот эти углы
Они спокойно получатся сами, если вертикальную ось продолжить дальше.
Во-вторых, в качестве единицы по вертикали я буду использовать стандартное отклонение, а в качестве оси - медиану цены. Получается примерно такое.
Вместо квадрата у нас получается прямоугольник. А углы показывают (примерно) границы броуновского движения цены.
ну что ж
интересный подход
Вместо квадрата у нас получается прямоугольник. А углы показывают (примерно) границы броуновского движения цены.
??? когда броуновское движение и некие его границы то вот что-что, но только не прямоугольник :-) Это такая матчастная матчасть, которая должна "от зубов отлетать". Как таблица умножения.
фигура довольно близкая к ромбу получается от сезонной волатильности (день-неделя-месяц-квартал). И это получится "расшифровка" углов и сеток Гана без мистических квадратов и кручения столов. Можете статистикой вывести
робот торгующий по принципу похожему на ваш скриншот :
Еще один способ получить углы из цены. Спасибо дедушке Ганну.
Еще один способ получить углы из цены. Спасибо дедушке Ганну.
странное значение угла
Еще один способ получить углы из цены. Спасибо дедушке Ганну.
Коробка (шаблон) намного удобнее, т.к. вы сразу получаете и ценовые и временные уровни (отсечки). Да и внутри дня точнее всего квадрировать прошлое движение, самая маленькая погрешность в расчетах получается.