MetaTrader 5 / Интеграция
English 中文 Español Deutsch 日本語 Português
preview
Нейросети — это просто (Часть 22): Обучение без учителя рекуррентных моделей

Нейросети — это просто (Часть 22): Обучение без учителя рекуррентных моделей

MetaTrader 5 — Интеграция | 26 июля 2022, 12:49
2 214 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Содержание


    Введение

    Последние две статьи нашей серии были посвящены автоэнкодерам. Их архитектура позволяет обучать на неразмеченных данных различные модели нейронных сетей с использование алгоритма обратного распространения ошибки. При этом обучаемая модель учится сжимать исходные данные с выделением основных признаков. Проведенные нами эксперименты подтвердили результативность моделей автоэнкодера. И тут надо обратить внимание, что для тестирования автоэнкодеров мы использовали полносвязные нейронные слои. Как известно, такие модели работают с фиксированным окном исходных данных. Построенный нами алгоритм способен обучать любые модели, которые работают с фиксированным окном исходных данных. Но архитектура рекуррентных моделей немного иная: для принятия решения об активации нейронов помимо исходных данных они используют и своё предыдущее состояние. Следовательно, при построении автоэнкодера мы должны учитывать эту особенность.


    1. Особенности обучения рекуррентных моделей

    Для начала давайте немного вспомним про организацию рекуррентных моделей и их назначение. Посмотрите на график движения цены: на нем отображены исторические данные о движении цены. Каждый бар представляет собой описание границ диапазона, в котором колебалась цена инструмента в конкретный временной интервал. Заметьте, это "исторические данные", а значит, они уже не изменяются. С течением времени добавляются новые бары, но не изменяются старые. В каждый конкретный момент времени мы имеем неизменные исторические данные и одну не полностью сформированную последнюю свечу, которая может изменяться до закрытия её временного интервала.

    Ценовой график

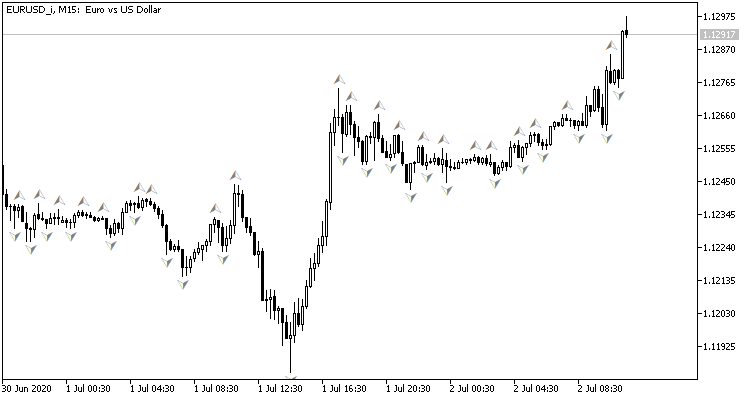
    Анализируя исторические данные, мы пытаемся спрогнозировать наиболее вероятное предстоящее движение цены. При этом глубина анализируемой истории варьируется в каждом конкретном случае. И в этом, наверное, одна из основных проблем использования нейронных сетей с фиксированным размером исходных данных — относительно маленькое окно анализа исторических данных ограничивает возможности анализа. А чрезмерно большое окно усложняет саму модель и процесс её обучения. Поэтому, при выборе размера окна исходных данных архитектор такой модели вынужден идти на компромисс и определить "золотую середину".

    В то же время мы имеем дело с историческими данными. Какой бы размер окна мы ни выбрали, на каждой итерации работы нашей модели практически более 99% информации мы будем передавать ей повторно. А она, в свою очередь, будет их повторно обрабатывать. И это похоже на неэффективное использование ресурсов. Но ни полносвязные, ни сверточные модели ничего не помнят о ранее обработанной информации.

    Решение вышеуказанных проблем было найдено в использовании рекуррентных нейронов. Идея заключалась в том, что состояние каждого нейрона зависит от результата обработки исходных данных. Следовательно, можно предположить, что состояние нейрона является некой сжатой формой исходных данных. А значит, мы можем на вход нейрона вместе с исходными данным подать и его предыдущее состоянии. Таким образом, новое состояния нейрона будет зависеть как от текущего состояния анализируемой системы, так и от предыдущего, информация о котором в сжатом виде заключено в предыдущем состоянии нейрона. 

    Рекуррентная модель

    Оказалось, что такой подход позволяет модели запоминать несколько состояний системы. При этом использование функций активации и весовых коэффициентов, абсолютное значение которых меньше 1, постепенно снижает влияние наиболее ранних исторических данных. В результате мы имеем модель с довольно прогнозируемым горизонтом памяти.

    Наличие подобных моделей с памятью позволяет не ограничиваться используемым окном исторических данных для принятия решения и уменьшить объем повторно передаваемой информации, т.к. о ней модель уже будет помнить. Благодаря этим свойствам рекуррентные модели являются одним из приоритетных направлений в решении задач обработки временных рядов.

    В то же время использование этих особенностей требует и особых подходов в обучении рекуррентных моделей. К примеру, возвращаясь к архитектуре автоэнкодеров, если мы на рисунке выше приравняем вход Xi и выход Yi модели, то для восстановления исходных данных из латентного состояния модели нет необходимости вспоминать предыдущее состояние. Поэтому в процессе обучения модель обнулит влияние исторических данных и будет оценивать только текущее состояние. Утратив способность помнить, рекуррентная модель лишается основного своего преимущества.

    Следовательно, при проработке архитектуры нашей модели мы должны учитывать этот факт и организовать процесс обучения таким образом, чтобы модель была вынуждена обращаться данным предыдущих итераций.

    Наверное, надо сказать, что при построении автоэнкодеров, в большинстве случаев, архитектура декодерах практически зеркально повторяет архитектуру энкодера. И в случае с рекуррентными моделями сохраняется эта практика. Но, как ни странно, одна из первых подобных архитектур была использована для обучения с учителем. В работе " Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation" авторы предложили RNN Encoder-Decoder в качестве модели для статистического машинного перевода. Энкодер и декодер данной модели представляли собой рекуррентные сети. Энкодер сжимал фразу исходного языка до некоего латентного состояния. А затем декодер "разворачивал" его до фразы на целевом языке перевода. Очень напоминает автоэнкодер, не правда ли?

    Использование рекуррентной модели позволяло по одному слову передавать фразу в энкодер, что дало возможность обучать модель на фразах различной длины. После получения полной фразы энкодер передавал латентное состояние в декодер. И декодер также по одному слову, давал перевод фразы на целевом языке.

    После обучения на размеченных фразах английского и французского языков авторы получили модель, способную возвращать семантически и синтаксически осмысленные фразы.

    Непосредственно обучение без учителя рекуррентных моделей довольно хорошо представлено в статье "Unsupervised Learning of Video Representations using LSTMs", которая была опубликована в феврале 2015 года. Авторы указанной статьи провели ряд экспериментов с обучением рекуррентных автоэнкодеров на различных видео материалах. При этом осуществлялось как восстановление полученных на вход энкодера данных, так и прогнозирование вероятного продолжения видеоряда.

    В статье приводятся различные архитектуры автоэнкодеров. Но все они используют LSTM блоки как для кодирования, так и для декодирования сигнала. Надо сказать, что наилучшие результаты удалось добиться при обучении модели с 1-м энкодером и 2-мя декодерами. В ней один декодер отвечал за восстановление исходных данных. А второй декодер — за прогнозирование наиболее вероятного продолжения видеоряда.

    Использование рекуррентных блоков в энкодере позволяет по кадрам передавать в модель исходный видеоряд. А рекуррентные блоки декодера в зависимости от поставленной задачи по кадрам возвращают восстановленный или прогнозный видеоряд.

    Кроме того, авторы статьи показывают, что рекуррентные модели, предварительно обученные без учителя, позволяют получить довольно хорошие результаты в задачах распознавания движений на видео после дообучения модели с учителем даже на сравнительно небольшом объеме размеченных данных.

    Представленные в обоих статьях материалы позволяют нам надеяться на успешность подобного подхода и для решения наших задач.

    В то же время в своей реализации я сделаю небольшое отступление от предложенных моделей. Все они использовали рекуррентные блоки в декодере и по кадрам возвращали декодированные данные. Это вполне соответствовало задачам перевода и анализу видеопотока. Вероятно, это даст результаты для прогнозирования следующего бара. Но я пока не проводил подобных экспериментов. В общем же случае, при анализе рыночной ситуации мы оцениваем её как целостную картину, охватывающую довольно продолжительный временной интервал. Поэтому, мы планируем постепенно небольшими порциями передавать в модель изменения рыночной ситуация. А она, в свою очередь, должна оценить рыночную ситуацию с учетом текущих и полученных ранее данных. А значит, латентное состояние должно содержать информацию о как можно более широком временном интервале.

    Чтобы добиться такого эффекта, мы будем использовать рекуррентные блоки только в энкодере. В декодере я предлагаю использовать все те же полносвязные нейронные слои, только восстанавливать мы будем данные, переданные в энкодер, за несколько итераций.


    2. Реализация

    Далее мы переходим к практической части нашей статьи. Наш рекуррентный энкодер мы построим на базе рассмотренных ранее LSTM блоков, структура которого представлена на рисунке ниже. Как вы помните, данный блок состоит из 4-х полносвязных нейронных слоёв. Три из которых выполняют функционал ворот, регулирующих поток информации. И один выполняет роль преобразования исходных данных.

    В LSTM блоке используется 2 рекуррентных потока информации: память и скрытое состояние.

    Структура LSTM блока

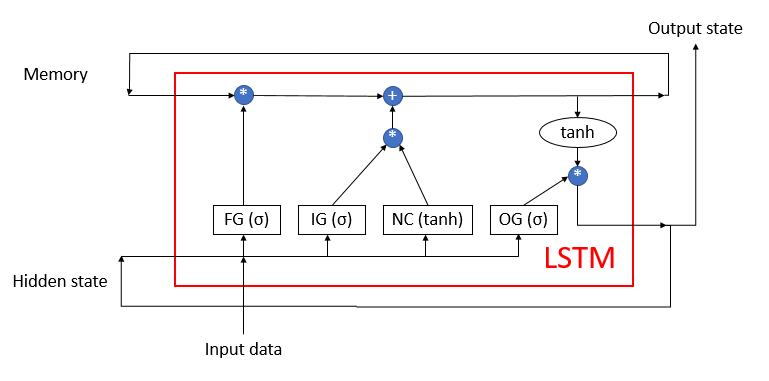
    Ранее мы уже воссоздали алгоритм LSTM блока средствами MQL5. Теперь же нам предстоит повторить его с использованием технологии OpenCL. Для его реализации мы создадим новый класс CNeuronLSTMOCL. Основной набор буферов и методов мы унаследуем у базового класса CNeuronBaseOCL, который мы будем использовать в качестве родительского класса.

    Структура методов и переменных класса представлена ниже. И если методы класса вполне узнаваемы. Это все те же методы прямого и обратного прохода, которые мы переопределяем в каждом новом классе. То назначение переменных, я думаю, надо проговорить.

    class CNeuronLSTMOCL : public CNeuronBaseOCL
  {
protected:
   CBufferFloat      m_cWeightsLSTM;
   CBufferFloat      m_cFirstMomentumLSTM;
   CBufferFloat      m_cSecondMomentumLSTM;

   int               m_iMemory;
   int               m_iHiddenState;
   int               m_iConcatenated;
   int               m_iConcatenatedGradient;
   int               m_iInputs;
   int               m_iWeightsGradient;
//---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronLSTMOCL(void);
                    ~CNeuronLSTMOCL(void);
//---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint numNeurons, ENUM_OPTIMIZATION optimization_type,
                          uint batch) override;
//---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
//---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
//---
   virtual int       Type(void) override const   {  return defNeuronLSTMOCL; }
  };

    Прежде всего мы здесь видим 3 буфера данных:

    • m_cWeightsLSTM — матрица весовых коэффициентов LSTM блока;
    • m_cFirstMomentumLSTM — матрица первых моментов обновления весовых коэффициентов;
    • m_cSecondMomentumLSTM  — матрица вторых моментов обновления весовых коэффициентов.

      Обратите внимание. Как уже было сказано выше, LSTM блок содержит 4 полносвязных нейронных слоя. В то же время мы объявляем только один буфер для матрицы весов m_cWeightsLSTM. На самом деле данный буфер будет содержать весовые коэффициенты всех 4-х нейронных слоев. А использование конкатенированного буфера позволит нам осуществить параллельное вычисление всех 4-х нейронных слоёв одновременно. Детальнее с механизмом организации параллелизма мы познакомимся немного позже при рассмотрении реализации каждого метода.

      То же самое относится и к буферам моментов m_cFirstMomentumLSTM и m_cSecondMomentumLSTM.

      Надо сказать, что в последних билдах терминала компания MetaQuotes Ltd внесла ряд улучшений. Они коснулись и используемой нами технологии OpenCL. В частности, было увеличено максимальное количество OpenCL объектов и добавлена возможность использования технологии на видеокартах без поддержки double. Это позволяет нам снизить общее время на обучение модели, так как теперь нет необходимости загружать данные из памяти CPU перед вызовом каждого кернела и не выгружать их обратно, после его выполнения. Достаточно лишь один раз загрузить все исходные данные в память контекста OpenCL перед началом обучения и скопировать полученный результат после окончания обучения.  

      Более того, это позволяет нам некоторые буферы объявлять только в контексте OpenCL без создания зеркального буфера в основной памяти устройства. Речь идет о буферах хранения временной информации. Поэтому для целого ряда буферов мы создадим лишь переменную для хранения указателя на буфер в контексте OpenCL:

      • m_iMemory — указатель на буфер памяти;
      • m_iHiddenState — указатель на буфер скрытого состояния;
      • m_iConcatenated — указатель на конкатенированный буфер результатов 4-х внутренних нейронных слоёв;
      • m_iConcatenatedGradient — указатель на конкатенированный буфер градиентов ошибки на уровне результатов 4-х внутренних нейронных слоёв;
      • m_iWeightsGradient  — указатель на буфер градиентов ошибки на уровне матрицы весов 4-х внутренних нейронных слоёв.

      Начальные значения всем переменных мы присвоим в конструкторе класса.

      CNeuronLSTMOCL::CNeuronLSTMOCL(void)   :  m_iMemory(-1),
                                          m_iConcatenated(-1),
                                          m_iConcatenatedGradient(-1),
                                          m_iHiddenState(-1),
                                          m_iInputs(-1)
  {}

      В свою очередь в деструкторе класса мы освободим все используемые буфера.

      CNeuronLSTMOCL::~CNeuronLSTMOCL(void)
  {
   if(!OpenCL)
      return;
   OpenCL.BufferFree(m_iConcatenated);
   OpenCL.BufferFree(m_iConcatenatedGradient);
   OpenCL.BufferFree(m_iHiddenState);
   OpenCL.BufferFree(m_iMemory);
   OpenCL.BufferFree(m_iWeightsGradient);
   m_cFirstMomentumLSTM.BufferFree();
   m_cSecondMomentumLSTM.BufferFree();
   m_cWeightsLSTM.BufferFree();
  }

      Мы продолжаем работу над методами нашего класса и создадим метод инициализации объекта нашего LSTM блока. Соблюдая правила наследования, мы переопределим метод CNeuronLSTMOCL::Init с полным сохранением параметров аналогичного метода родительского класса. В параметрах наш метод инициализации получит количество нейронов следующего слоя, индекс нейрона, указатель на объект контекста OpenCL, количество нейронов текущего слоя, метод оптимизации параметров и размер пакета.

      В теле метода мы сначала вызываем аналогичный метод родительского класса. Что позволит нам инициализировать унаследованные объекты родительского класса, а также осуществить контроль полученных исходных данных. И, конечно, мы сразу проверяем результат выполнения операций.

      Далее нам необходимо осуществить инициализацию объявленных выше буферов данных. Тут надо сказать, что на данном этапе мы не сможем осуществить полную инициализацию всех буферов. Нам банально не хватает исходных данных. В параметрах мы получили количество нейронов текущего слоя и количество нейронов в последующем слое. Но мы не знаем количества нейронов в предыдущем слое. Поэтому не знаем размера буфера, необходимого для хранения весовых коэффициентов нашего LSTM блока. Поэтому на данном этапе мы создаем только те буферы данных, размер которых зависит только от количества элементов в текущем слое.

      bool CNeuronLSTMOCL::Init(uint numOutputs, uint myIndex,
                          COpenCLMy *open_cl, uint numNeurons,
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;
//---
   m_iMemory = OpenCL.AddBuffer(sizeof(float) * numNeurons * 2, CL_MEM_READ_WRITE);
   if(m_iMemory < 0)
      return false;
   m_iHiddenState = OpenCL.AddBuffer(sizeof(float) * numNeurons, CL_MEM_READ_WRITE);
   if(m_iHiddenState < 0)
      return false;
   m_iConcatenated = OpenCL.AddBuffer(sizeof(float) * numNeurons * 4, CL_MEM_READ_WRITE);
   if(m_iConcatenated < 0)
      return false;
   m_iConcatenatedGradient = OpenCL.AddBuffer(sizeof(float) * numNeurons * 4, CL_MEM_READ_WRITE);
   if(m_iConcatenatedGradient < 0)
      return false;
//---
   return true;
  }

      И, конечно, не забываем контролировать процесс выполнения операций на каждом шаге.

      После создания методов инициализации объекта мы переходим к организации прямого прохода нашего LSTM блока. Как вы знаете, при использовании технологии OpenCL непосредственно вычисления осуществляются в контексте OpenCL на GPU. В коде же основной программы мы лишь осуществляем вызов необходимой программы. Поэтому, перед написанием метода нашего класса нам необходимо дополнить соответствующим кернелом нашу OpenCL программу.

      За организацию прямого прохода в OpenCL программе будет отвечать кернел LSTM_FeedForward. Для корректной организации процесса нам потребуется предать в кернел указатели на 5 буферов данных и одну константу:

      • inputs — буфер исходных данных:
      • inputs_size — количество элементов в буфере исходных данных;
      • weights — буфер матрицы весов;
      • concatenated — конкатенированный буфер результатов всех внутренних нейронных слоёв;
      • memory — буфер памяти;
      • output — буфер результатов (он же буфер скрытого состояния).

      __kernel void LSTM_FeedForward(__global float* inputs, uint inputs_size,
                               __global float* weights,
                               __global float* concatenated,
                               __global float* memory,
                               __global float* output
                              )
  {
   uint id = (uint)get_global_id(0);
   uint total = (uint)get_global_size(0);
   uint id2 = (uint) get_local_id(1);

      Запускать мы будем буфер в 2-мерном пространстве задач. В первом измерении мы укажем количество элементов в текущем LSTM блоке. А второе измерение равно 4-м потокам по числу внутренних нейронных слоёв. Здесь хочу напомнить, что количество элементов в нашем LSTM блоке определяет как количество элементов в каждом из внутренних слоёв, так и количество элементов в памяти и скрытом состоянии.

      Поэтому, в теле кернела мы первым делом определяем порядковый номер потока в каждом измерении. А также общее количество задач в первом измерении.

      Надо добавить, что весь процесс прямого прохода LSTM блока можно условно разделить на 2 подпроцесса:

      • вычисление значений внутренних нейронных слоёв;
      • организация потока данных от нейронных слоёв до выхода из LSTM блока.

      И выполнение второго подпроцесса невозможно до полного окончания первого. А точнее, для выполнения 2-го подпроцесса нужны значения всех 4-х нейронных слоёв, как минимум, в рамках текущего элемента LSTM блока. Поэтому нам нужна синхронизация потоков по второму измерению. текущая реализация OpenCL позволяет осуществлять синхронизацию потоков в рамках локальной группы. А значит, мы будем строить наши локальные группы по 2-му измерению задач.

      Далее мы организуем расчет взвешенной суммы исходных данных и скрытого состояния. Вначале мы посчитаем взвешенную сумму скрытого состояния.

         float sum = 0;
   uint shift = (id + id2 * total) * (total + inputs_size + 1);
   for(uint i = 0; i < total; i += 4)
     {
      if(total - i > 4)
         sum += dot((float4)(output[i], output[i + 1], output[i + 2], output[i + 3]),
                    (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3]));
      else
         for(uint k = i; k < total; k++)
            sum += output[k] + weights[shift + k];
     }

      А затем прибавим взвешенную сумму исходных данных.

         shift += total;
   for(uint i = 0; i < inputs_size; i += 4)
     {
      if(total - i > 4)
         sum += dot((float4)(inputs[i], inputs[i + 1], inputs[i + 2], inputs[i + 3]),
                    (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3]));
      else
         for(uint k = i; k < total; k++)
            sum += inputs[k] + weights[shift + k];
     }
   sum += weights[shift + inputs_size];

      И в заключение добавим значение нейрона смещения.

      После вычисления взвешенной суммы нам необходимо вычислить значение функции активации. Напомню, что для ворот в качестве функции активации используется сигмоида. А для слоя нового контента — гиперболический тангенс. Необходимую функцию активации будем определять по идентификатору потока во втором измерении.

         if(id2 < 3)
      concatenated[id2 * total + id] = 1.0f / (1.0f + exp(sum));
   else
      concatenated[id2 * total + id] = tanh(sum);
//---
   barrier(CLK_LOCAL_MEM_FENCE);

      Как уже было сказано выше, для корректного выполнения алгоритма нам необходима синхронизация потоков по 2-му измерению пространства задач. Для синхронизации потоков мы воспользуемся функцией barrier.

      Для организации процесса передачи информации между внутренними слоями нам достаточно одного потока для каждого элемента LSTM блока. Поэтому, после синхронизации потоков процесс будет осуществляться только для потока с "0"-м идентификатором потока во втором измерении пространства задач.

         if(id2 == 0)
     {
      float mem = memory[id + total] = memory[id];
      float fg = concatenated[id];
      float ig = concatenated[id + total];
      float og = concatenated[id + 2 * total];
      float nc = concatenated[id + 3 * total];
      //---
      memory[id] = mem = mem * fg + ig * nc;
      output[id] = og * tanh(mem);
     }
//---
  }

      На этом мы заканчиваем работу с кернелом прямого прохода и можем осуществить его вызов из основной программы. Вначале мы создадим необходимые константы.

      #define def_k_LSTM_FeedForward            32
#define def_k_lstmff_inputs               0
#define def_k_lstmff_inputs_size          1
#define def_k_lstmff_weights              2
#define def_k_lstmff_concatenated         3
#define def_k_lstmff_memory               4
#define def_k_lstmff_outputs              5

      А затем можем приступить к созданию метода прямого прохода нашего класса. Как и аналогичный метод любого другого ранее рассмотренного класса, в параметрах метод получает указатель на объект предыдущего нейронного слоя. И в теле метода мы сразу организовываем проверку полученного указателя.

      bool CNeuronLSTMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || NeuronOCL.Neurons() <= 0 ||
      NeuronOCL.getOutputIndex() < 0 || !OpenCL)
      return false;

      Далее надо вспомнить, что при инициализации класса мы смогли инициализировать не все буферы данных. Незнание количества нейронов предыдущего слоя не позволило нам это сделать. Сейчас же мы получили указатель на предыдущий нейронный слой. А значит может запросить количество нейронов в этом слое и создать недостающие буфера данных. Но прежде, чем это сделать, мы проверим, что буфера ещё не созданы. Ведь это может быть не первый вызов метода прямого прохода. Своеобразным флагом у нас будет выступать переменная, содержащая количество элементов в предыдущем слое.

         if(m_iInputs <= 0)
     {
      m_iInputs = NeuronOCL.Neurons();
      int count = (int)((m_iInputs + Neurons() + 1) * Neurons());
      if(!m_cWeightsLSTM.Reserve(count))
         return false;
      float k = (float)(1 / sqrt(Neurons() + 1));
      for(int i = 0; i < count; i++)
        {
         if(!m_cWeightsLSTM.Add((2 * GenerateWeight()*k - k)*WeightsMultiplier))
            return false;
        }
      if(!m_cWeightsLSTM.BufferCreate(OpenCL))
         return false;
      //---
      if(!m_cFirstMomentumLSTM.BufferInit(count, 0))
         return false;
      if(!m_cFirstMomentumLSTM.BufferCreate(OpenCL))
         return false;
      //---
      if(!m_cSecondMomentumLSTM.BufferInit(count, 0))
         return false;
      if(!m_cSecondMomentumLSTM.BufferCreate(OpenCL))
         return false;
      if(m_iWeightsGradient >= 0)
         OpenCL.BufferFree(m_iWeightsGradient);
      m_iWeightsGradient = OpenCL.AddBuffer(sizeof(float) * count, CL_MEM_READ_WRITE);
      if(m_iWeightsGradient < 0)
         return false;
     }
   else
      if(m_iInputs != NeuronOCL.Neurons())
         return false;

      После завершения подготовительной работы мы передаем указатели на буфера данных и значение необходимой константы в параметры кернела прямого прохода. При этом не забываем контролировать процесс выполнения операций.

         if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_inputs, NeuronOCL.getOutputIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_concatenated, m_iConcatenated))
      return false;
   if(!OpenCL.SetArgument(def_k_LSTM_FeedForward, def_k_lstmff_inputs_size, m_iInputs))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_memory, m_iMemory))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_outputs, getOutputIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_weights, m_cWeightsLSTM.GetIndex()))
      return false;

      Далее мы зададим пространство задач и сдвиг в нем до 1-й итерации. Обратите внимание, что в данном случае мы задаем пространство задач в 2-х измерениях и размер объединяемых локальных групп в 2-х измерениях. И если в первом случае мы указываем общее количество элементов текущего слоя в 1-м измерении. То для локальном группы в первом измерении мы указываем только один элемент. При этом во втором измерении в обоих случаях мы указываем 4 элемента, по числу внутренних нейронных слоев. Это позволяет создать нам локальные группы по 4 потока в каждой. А число таких локальных групп будет равно числу элементов в текущем нейронном слое.

         uint global_work_offset[] = {0, 0};
   uint global_work_size[] = {Neurons(), 4};
   uint local_work_size[] = {1, 4};

      Таким образом, осуществляя синхронизацию потоков в каждой локальной группе мы синхронизируем вычисления значений всех 4-х внутренних нейронных слоёв в разрезе каждого отдельно взятого элемента текущего слоя. А этого вполне достаточно для организации корректного вычисления прямого прохода всего LSTM блока.

      Далее нам остается лишь поставить наш кернел в очередь выполнения.

         if(!OpenCL.Execute(def_k_LSTM_FeedForward, 2, global_work_offset, global_work_size, local_work_size))
      return false;
//---
   return true;
  }

      На этом мы заканчиваем работу над прямым проходом нашего LSTM блока, и мы можем перейти к организации обратного прохода. И тут, как и в случае с прямым проходом, перед созданием методов нашего класса мы должны дополнить OpenCL программу. И если весь прямой проход нам удалось объединить в один кернел, то в случае обратного прохода нам потребуется целых 3 кернела.

      В первом кернеле LSTM_ConcatenatedGradient будет организовано распределение градиента до уровня результатов внутренних нейронных слоёв. В параметрах кернел получает указатели на 4 буфера данных. 3 из них будут содержать исходные данные: буфер градиентов от последующего слоя, состояние памяти и конкатенированный буфер результатов внутренних нейронных слоев. Четвертый буфер будет использоваться для записи результатов работы кернела.

      Кернел будет вызываться в 1-мерном пространстве задач по числу элементов в нашем LSTM блоке.

      В теле кернела мы сначала определяем идентификатор поток и их общее количество. А затем, двигаясь по пути обратного прохождения сигнала, мы определяем градиент ошибки на уровне результата выходных врат, на уровне памяти, на уровне нейронного слоя нового контента, на уровне врат нового контента. И далее на уровне врат забвения.

      __kernel void LSTM_ConcatenatedGradient(__global float* gradient,
                                        __global float* concatenated_gradient,
                                        __global float* memory,
                                        __global float* concatenated
                                       )
  {
   uint id = get_global_id(0);
   uint total = get_global_size(0);
   float t = tanh(memory[id]);
   concatenated_gradient[id + 2 * total] = gradient[id] * t;             //output gate
   float memory_gradient = gradient[id] * concatenated[id + 2 * total];
   memory_gradient *= 1 - pow(t, 2.0f);
   concatenated_gradient[id + 3 * total] = memory_gradient * concatenated[id + total];         //new content
   concatenated_gradient[id + total] = memory_gradient * concatenated[id + 3 * total]; //input gate
   concatenated_gradient[id] = memory_gradient * memory[id + total];     //forgat gate
  }

      После этого нам предстоит провести градиент ошибки через внутренние слои LSTM блока до предыдущего нейронного слоя. Для этого мы создадим следующий кернел LSTM_HiddenGradient. Надо сказать, что при проработке архитектуры OpenCL программы было решено в рамках данного кернеле объединить распределения градиента до уровня предыдущего слоя и до уровня матрицы весов. Поэтому, в параметрах он получает указатели на 6 буферов данных и 2 константы. Вызывать кернел планируется в одномерном пространстве задач. 

      __kernel void LSTM_HiddenGradient(__global float* concatenated_gradient,
                                  __global float* inputs_gradient,
                                  __global float* weights_gradient,
                                  __global float* hidden_state,
                                  __global float* inputs,
                                  __global float* weights,
                                  __global float* output,
                                  const uint hidden_size,
                                  const uint inputs_size
                                 )
  {
   uint id = get_global_id(0);
   uint total = get_global_size(0);

      В теле кернела мы определяем идентификатор потока и общее количество потоков. Тут же мы определяем размер одного вектора матрицы весов.

         uint weights_step = hidden_size + inputs_size + 1;

      Далее мы организовываем цикл по перебору всех элементов конкатенированного буфера исходных данных, который включает скрытое состояние и текущее состоянии, полученное от предыдущего нейронного слоя. Стоит отметить, что итерации цикла начинаются от текущего идентификатора потока и шаг итераций цикла равен общему количеству запущенных потоков. Такой подход позволяет перебрать все элементы конкатенированного слоя исходных данных независимо от количества запущенных потоков.

         for(int i = id; i < (hidden_size + inputs_size); i += total)
     {
      float inp = 0;

      На этом шаге в теле цикла мы организовываем разделение потока операций в зависимости от анализируемого элемента. Если анализируемый элемент относится к скрытому состоянию, то мы сохраним скрытое состояние в частную переменную. А в буфер перенесем соответствующее значение из буфера результатов. Так как на следующей итерации оно уже будет в скрытом состояние.

            if(i < hidden_size)
        {
         inp = hidden_state[i];
         hidden_state[i] = output[i];
        }

      Если же текущий элемент относится к буферу исходных данных предыдущего нейронного слоя, то мы перенесем значение исходных данных в частную переменную и посчитаем градиент ошибки для соответствующего нейрона предыдущего слоя.

            else
        {
         inp = inputs[i - hidden_size];
         float grad = 0;
         for(uint g = 0; g < 3 * hidden_size; g++)
           {
            float temp = concatenated_gradient[g];
            grad += temp * (1 - temp) * weights[i + g * weights_step];
           }
         for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++)
           {
            float temp = concatenated_gradient[g];
            grad += temp * (1 - pow(temp, 2.0f)) * weights[i + g * weights_step];
           }
         inputs_gradient[i - hidden_size] = grad;
        }

      После распределения градиента ошибки на предыдущий нейронный слой мы распределим градиент ошибки на соответствующие весовые коэффициента LSTM блока.

            for(uint g = 0; g < 3 * hidden_size; g++)
        {
         float temp = concatenated_gradient[g];
         weights[i + g * weights_step] = temp * (1 - temp) * inp;
        }
      for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++)
        {
         float temp = concatenated_gradient[g];
         weights[i + g * weights_step] = temp * (1 - pow(temp, 2.0f)) * inp;
        }
     }

      В заключении кернела, мы аналогичным способом перенесем градиент ошибки на нейроны смещения каждого вектора весовых коэффициентов.

         for(int i = id; i < 4 * hidden_size; i += total)
     {
      float temp = concatenated_gradient[(i + 1) * hidden_size];
      if(i < 3 * hidden_size)
         weights[(i + 1) * weights_step] = temp * (1 - temp);
      else
         weights[(i + 1) * weights_step] = 1 - pow(temp, 2.0f);
     }
  }

      После распределения градиента ошибки до уровня предыдущего нейронного слоя и матрицы весов, нам необходимо ещё реализовать процесс обновления весовых коэффициентов. Я не стал реализовывать полный спектр методов оптимизации параметров. И решил в рамках данного класса реализовать только наиболее часто используемый мной метод Adam. Вы же по аналогии с моей реализацией сможете добавить любой другой метод оптимизации параметров модели.

      Итак, обновление параметров модели осуществляется в кернеле LSTM_UpdateWeightsAdam. Напомню, что градиент ошибки на уровне матрицы весов мы уже посчитали в предыдущем кернеле и записали в буфер weights_gradient. Поэтому, в данном кернеле нам остаётся лишь организовать непосредственно процесс обновления параметров модели. Для осуществления процесса обновления параметров методом Adam нам потребуются 2 дополнительных буфера для записи первого и второго момента. Кроме того, нам понадобятся гиперпараметры обучения. И все эти данные мы будем передавать в параметрах кернела.

      __kernel void LSTM_UpdateWeightsAdam(__global float* weights,       
                                     __global float* weights_gradient,
                                     __global float *matrix_m,        
                                     __global float *matrix_v,        
                                     const float l,                   
                                     const float b1,                  
                                     const float b2                   
                                    )
  {
   const uint id = get_global_id(0);
   const uint total = get_global_size(0);
   const uint id1 = get_global_id(1);
   const uint wi = id1 * total + id;

      Как вы знаете, матрица весов представляет из себя 2-мерную матрицу. Поэтому и вызов кернела мы будем осуществлять в 2-мерном пространстве задач.

      В теле кернела мы, как всегда, определяем порядковый номер потока в обоих измерениях и общее количество потоков, запущенных в первом измерении. По этим константам мы определяем сдвиг в буферах до анализируемого весового коэффициента. И далее выполняем алгоритм обновления соответствующего элемента матрицы весовых коэффициентов.

         float g = weights_gradient[wi];
   float mt = b1 * matrix_m[wi] + (1 - b1) * g;
   float vt = b2 * matrix_v[wi] + (1 - b2) * pow(g, 2);
   float delta = l * (mt / (sqrt(vt) + 1.0e-37f) - (l1 * sign(weights[wi]) + l2 * weights[wi] / total));
   weights[wi] = clamp(weights[wi] + delta, -MAX_WEIGHT, MAX_WEIGHT);
   matrix_m[wi] = mt;
   matrix_v[wi] = vt;
  };

      На этом мы заканчиваем работу по внесению изменений в OpenCL программу и переходим к реализации методов на стороне основной программы.

      Как и в случае с методом прямого прохода, сначала мы создадим константы для работы с выше созданными кернелами.

      #define def_k_LSTM_ConcatenatedGradient   33
#define def_k_lstmcg_gradient             0
#define def_k_lstmcg_concatenated_gradient 1
#define def_k_lstmcg_memory               2
#define def_k_lstmcg_concatenated         3

      #define def_k_LSTM_HiddenGradient         34
#define def_k_lstmhg_concatenated_gradient 0
#define def_k_lstmhg_inputs_gradient      1
#define def_k_lstmhg_weights_gradient     2
#define def_k_lstmhg_hidden_state         3
#define def_k_lstmhg_inputs               4
#define def_k_lstmhg_weeights             5
#define def_k_lstmhg_output               6
#define def_k_lstmhg_hidden_size          7
#define def_k_lstmhg_inputs_size          8

      #define def_k_LSTM_UpdateWeightsAdam      35
#define def_k_lstmuw_weights              0
#define def_k_lstmuw_weights_gradient     1
#define def_k_lstmuw_matrix_m             2
#define def_k_lstmuw_matrix_v             3
#define def_k_lstmuw_l                    4
#define def_k_lstmuw_b1                   5
#define def_k_lstmuw_b2                   6

      После этого мы переходим к работе над методами нашего класса. И первым мы создадим метод распределения градиента ошибки calcInputGradients. В параметрах метод получает указатель на объект предыдущего нейронного слоя. И мы сразу проверяем действительность полученного указателя.

      bool CNeuronLSTMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || NeuronOCL.Neurons() <= 0 || NeuronOCL.getGradientIndex() < 0 ||
      NeuronOCL.getOutputIndex() < 0 || !OpenCL)
      return false;

      Затем мы проверяем наличие необходимых буферов данных в контексте OpenCL.

         if(m_cWeightsLSTM.GetIndex() < 0 || m_cFirstMomentumLSTM.GetIndex() < 0 ||
      m_cSecondMomentumLSTM.GetIndex() < 0)
      return false;
   if(m_iInputs < 0 || m_iConcatenated < 0 || m_iMemory < 0 ||
      m_iConcatenatedGradient < 0 || m_iHiddenState < 0 || m_iInputs != NeuronOCL.Neurons())
      return false;

      И только после успешного прохождения всех контролей мы переходим к работе по вызову кернела. В соответствии с алгоритмом распределения градиента первым мы будем вызывать кернел LSTM_ConcatenatedGradient.

      Вначале мы организуем передачу исходных данных в параметры кернела.

         if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_concatenated, m_iConcatenated))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_concatenated_gradient, m_iConcatenatedGradient))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_gradient, getGradientIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_memory, m_iMemory))
      return false;

      Определим размерность пространства задач. И поставим кернел в очередь выполнения.

         uint global_work_offset[] = {0};
   uint global_work_size[] = {Neurons()};
   if(!OpenCL.Execute(def_k_LSTM_ConcatenatedGradient, 1, global_work_offset, global_work_size))
      return false;

      Тут же мы организуем и вызов второго кернела распределения градиента ошибки LSTM_HiddenGradient. Передадим параметры кернелу.

         if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_concatenated_gradient, m_iConcatenatedGradient))
      return false;
   if(!OpenCL.SetArgument(def_k_LSTM_HiddenGradient, def_k_lstmhg_hidden_size, Neurons()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_hidden_state, m_iHiddenState))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs, NeuronOCL.getOutputIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs_gradient, NeuronOCL.getGradientIndex()))
      return false;
   if(!OpenCL.SetArgument(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs_size, m_iInputs))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_output, getOutputIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_weeights, m_cWeightsLSTM.GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_weights_gradient, m_iWeightsGradient))
      return false;

      А далее, воспользуемся уже созданными массивами для указания пространства задач и просто поставим кернел в очередь выполнения.

         if(!OpenCL.Execute(def_k_LSTM_HiddenGradient, 1, global_work_offset, global_work_size))
      return false;
//---
   return true;
  }

      Ещё раз хочу напомнить о необходимости контроля выполнения всех операций. Это позволит вам вовремя отследить появление ошибки и предотвратить критическое завершение программы в самый неподходящий момент.

      После распределения градиента ошибки, для завершения алгоритма обратного прохода нам остается реализовать метод обновления параметров модели updateInputWeights. В параметрах данный метод получает указатель на объект предыдущего слоя. Но хочу вам напомнить, что мы уже определили градиент ошибки на уровне матрицы весов. Поэтому, наличие указателя на объект предыдущего слоя больше связано с организацией переопределения методов, чем необходимостью передачи данных. В данном случае состояние полученного указателя абсолютно не влияет на результат работы метода и мы его даже не проверяем. Вместо этого мы проверяем наличие необходимых нам внутренних буферов в контексте OpenCL.

      bool CNeuronLSTMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || m_cWeightsLSTM.GetIndex() < 0 || m_iWeightsGradient < 0 ||
      m_cFirstMomentumLSTM.GetIndex() < 0 || m_cSecondMomentumLSTM.GetIndex() < 0)
      return false;

      Далее, по уже отработанной схеме мы передаем параметры кернелу.

         if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_weights, m_cWeightsLSTM.GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_weights_gradient, m_iWeightsGradient))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_matrix_m, m_cFirstMomentumLSTM.GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_matrix_v, m_cSecondMomentumLSTM.GetIndex()))
      return false;
   if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_l, lr))
      return false;
   if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_b1, b1))
      return false;
   if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_b2, b2))
      return false;

      Определяем пространство задач и осуществляем постановку кернела в очередь выполнения.

         uint global_work_offset[] = {0, 0};
   uint global_work_size[] = {m_iInputs + Neurons() + 1, Neurons()};
   if(!OpenCL.Execute(def_k_LSTM_UpdateWeightsAdam, 2, global_work_offset, global_work_size))
      return false;
//---
   return true;
  }

      На этом мы заканчивает работу по организации обратного прохода. Таким образом, наш класс CNeuronLSTMOCL готов к первому тестированию. Но мы же знаем, что обученную модель нужно уметь сохранить и в последующем восстановить до рабочего состояния. Поэтому мы дополним наш класс методами работы с файлами.

      Как и во всех ранее рассмотренных архитектурах нейронных слоёв за сохранения данных отвечает метод Save. В параметрах данный метод получает хендл файла для записи данных.

      В теле метода мы первым делом вызываем аналогичный метод родительского класса. Что позволяет нам практически одной строчкой кода осуществить все необходимые контроли и сохранить унаследованные от родительского класса объекты. И, конечно, мы сразу проверяем результат выполнения метода родительского класса.

      После этого мы сохраним количество нейронов в предыдущем слое. А также матрицы весовых коэффициентов и моментов.

      bool CNeuronLSTMOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
   if(FileWriteInteger(file_handle, m_iInputs, INT_VALUE) < sizeof(m_iInputs))
      return false;
   if(!m_cWeightsLSTM.BufferRead() || !m_cWeightsLSTM.Save(file_handle))
      return false;
   if(!m_cFirstMomentumLSTM.BufferRead() || !m_cFirstMomentumLSTM.Save(file_handle))
      return false;
   if(!m_cSecondMomentumLSTM.BufferRead() || !m_cSecondMomentumLSTM.Save(file_handle))
      return false;
//---
   return true;
  }

      После сохранения данных нам необходимо создать метод восстановления работоспособности объекта из сохраненных данных Load. Вы уже знаете, что считывание данных из файла осуществляется в строгом соответствии с последовательностью записи. Как и в методе сохранения данных, в параметрах наш метод получает хендл файла для считывания файла, и мы сразу вызываем аналогичный метод родительского класса.

      bool CNeuronLSTMOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

      Далее мы считываем количество нейронов в предыдущем слое и сохраненные ранее буфера весовых коэффициентов и моментов. При этом, после загрузки каждого буфера мы сразу инициируем создание зеркальных буферов данных в контексте OpenCL. И, конечно, не забываем контролировать процесс выполнения операций.

         m_iInputs = FileReadInteger(file_handle);
//---
   m_cWeightsLSTM.BufferFree();
   if(!m_cWeightsLSTM.Load(file_handle) || !m_cWeightsLSTM.BufferCreate(OpenCL))
      return false;
//---
   m_cFirstMomentumLSTM.BufferFree();
   if(!m_cFirstMomentumLSTM.Load(file_handle) || !m_cFirstMomentumLSTM.BufferCreate(OpenCL))
      return false;
//---
   m_cSecondMomentumLSTM.BufferFree();
   if(!m_cSecondMomentumLSTM.Load(file_handle) || !m_cSecondMomentumLSTM.BufferCreate(OpenCL))
      return false;

      На данном этапе хочу напомнить, что рассматриваемы метод должен не только считать данные из файла, но и восстановить полную функциональность обученной модели. Поэтому, после считывания данных из файла нам также предстоит создать временные буфера данных, информацию о которых мы не сохраняли в файл.

         if(m_iMemory >= 0)
      OpenCL.BufferFree(m_iMemory);
   m_iMemory = OpenCL.AddBuffer(sizeof(float) * 2 * Neurons(), CL_MEM_READ_WRITE);
   if(m_iMemory < 0)
      return false;
//---
   if(m_iConcatenated >= 0)
      OpenCL.BufferFree(m_iConcatenated);
   m_iConcatenated = OpenCL.AddBuffer(sizeof(float) * 4 * Neurons(), CL_MEM_READ_WRITE);
   if(m_iConcatenated < 0)
      return false;
//---
   if(m_iConcatenatedGradient >= 0)
      OpenCL.BufferFree(m_iConcatenatedGradient);
   m_iConcatenatedGradient = OpenCL.AddBuffer(sizeof(float) * 4 * Neurons(), CL_MEM_READ_WRITE);
   if(m_iConcatenatedGradient < 0)
      return false;
//---
   if(m_iHiddenState >= 0)
      OpenCL.BufferFree(m_iHiddenState);
   m_iHiddenState = OpenCL.AddBuffer(sizeof(float) * Neurons(), CL_MEM_READ_WRITE);
   if(m_iHiddenState < 0)
      return false;
//---
   if(m_iWeightsGradient >= 0)
      OpenCL.BufferFree(m_iWeightsGradient);
   m_iWeightsGradient = OpenCL.AddBuffer(sizeof(float) * m_cWeightsLSTM.Total(), CL_MEM_READ_WRITE);
   if(m_iWeightsGradient < 0)
      return false;
//---
   return true;
  }

      На этом мы заканчиваем работу с методами класса CNeuronLSTMOCL. 

      Далее нам остаётся лишь добавить новые кернелы в процедуре подключения контекста OpenCL и указатели на новый тип нейронных слоев в диспетчерских методах нашего базового нейронного слоя.

      С полным перечнем всех методов данного и всех рассмотренных ранее классов можно ознакомиться во вложении.


      3. Тестирование

      После завершения работы над новым классом нейронного слоя мы переходим к созданию модели для тестового обучения. Новую модель мы рекуррентного автоэнкодера мы построили на базе модели вариационного автоэнкодера из предыдущей статьи. Для этого мы взяли указанную модель и сохранили в новый файл с именем "rnn_vae.mq5". В коде программы мы изменили архитектуру энкодера, добавив туда рекуррентные LSTM блоки.

      Обратите внимание, что на вход нашего рекуррентного энкодера мы подаем только последние 10 свечей.

      int OnInit()
  {
//---
 ..................
 ..................
//---
   Net = new CNet(NULL);
   ResetLastError();
   float temp1, temp2;
   if(!Net || !Net.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false))
     {
      printf("%s - %d -> Error of read %s prev Net %d", __FUNCTION__, __LINE__, FileName + ".nnw", GetLastError());
      HistoryBars = iHistoryBars;
      CArrayObj *Topology = new CArrayObj();
      if(CheckPointer(Topology) == POINTER_INVALID)
         return INIT_FAILED;
      //--- 0
      CLayerDescription *desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      int prev = desc.count = 10 * 12;
      desc.type = defNeuronBaseOCL;
      desc.optimization = ADAM;
      desc.activation = None;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 1
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = prev;
      desc.batch = 1000;
      desc.type = defNeuronBatchNormOCL;
      desc.activation = None;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 2
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      prev = desc.count = 500;
      desc.type = defNeuronLSTMOCL;
      desc.activation = None;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 3
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      prev = desc.count = prev/2;
      desc.type = defNeuronLSTMOCL;
      desc.activation = None;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 4
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      prev = desc.count = 50;
      desc.type = defNeuronLSTMOCL;
      desc.activation = None;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 5
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = prev/2;
      desc.type = defNeuronVAEOCL;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 6
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = (int) HistoryBars;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 7
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = (int) HistoryBars * 2;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 8
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = (int) HistoryBars * 4;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //--- 9
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = (int) HistoryBars * 12;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      delete Net;
      Net = new CNet(Topology);
      delete Topology;
      if(CheckPointer(Net) == POINTER_INVALID)
         return INIT_FAILED;
      dError = FLT_MAX;
     }
   else
     {
      CBufferFloat *temp;
      Net.getResults(temp);
      HistoryBars = temp.Total() / 12;
      delete temp;
     }
//---
 ..................
 ..................
//---
   return(INIT_SUCCEEDED);
  }

      Кроме того, как обсуждалось в данной статье выше, для организации обучения рекуррентного блока нам необходимо добавить условия, когда модель будет просто обязана заглянуть в "память". Поэтому для целей обучения мы создадим стек данных. И после каждой итерации прямого прохода мы будем удалять из стека информацию о наиболее старой свече и дописывать в конец стека информацию о новой свече.

      Таким образом, наш стек будет всегда содержать информацию о нескольких исторических состояниях анализируемой модели. И глубина такой истории будет определяться внешним параметром. Именно этот стек мы буем давать автоэнкодеру в качестве целевых значений. А превышение размера стека над величиной исходных данных на входе энкодера заставит наш автоэнкодер заглянуть в память прошлых состояний. 

       ..................
 ..................
         Net.feedForward(TempData, 12, true);
         TempData.Clear();
         if(!Net.GetLayerOutput(1, TempData))
            break;
         uint check_total = check_data.Total();
         if(check_total >= check_count)
           {
            if(!check_data.DeleteRange(0, check_total - check_count + 12))
               return;
           }
         for(int t = TempData.Total() - 12 - 1; t < TempData.Total(); t++)
           {
            if(!check_data.Add(TempData.At(t)))
               return;
           }
         if((total-it)>(int)HistoryBars)
            Net.backProp(check_data);
 ..................
 ..................

      Тестирование модели проводилось с сохранением всех используемых ранее параметров: инструмент EURUSD, таймфрейм H1, период тестирования — последние 15 лет. Параметры индикаторов по умолчанию. На вход энкодера подается информация о 10 последних свечах. При этом декодер обучается на дешифровку 40 последних свечей. Результаты тестирования представлены на графике ниже. На вход энкодера подаются данные после окончания формирования каждой новой свечи.

      Результаты обучения RNN-автоэнкоера

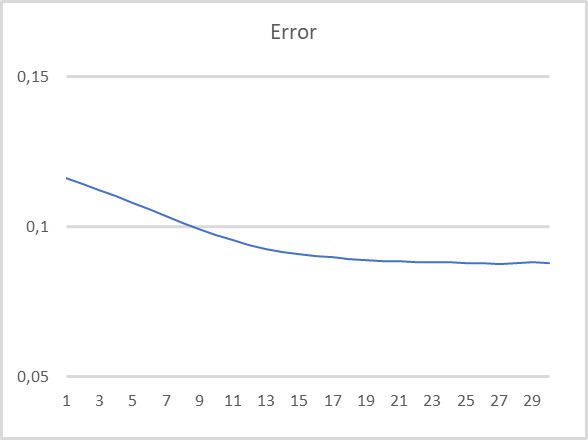
      Как можно заметить на графике, результаты тестирования подтверждают состоятельность такого подхода для предварительного обучения без учителя рекуррентных моделей. В процессе тестового обучения нашей модели, после 20 эпох обучения ошибка модели практически стабилизировалась с уровнем потерь менее 9%. При этом надо сказать, что в латентном состоянии модели хранится информация о, как минимум, 30 предшествующих итерациях.


      Заключение

      В данной статье мы с вами познакомились с проблематикой обучения рекуррентных моделей с использованием автоэнкодеров. В практической части статьи и создали рекуррентный автоэнкодер и провели его тестовое обучение. Результаты нашего эксперимента позволяют сделать вывод о состоятельности предложенного подхода к обучению рекуррентных моделей без учителя с использованием автоэнкодеров. При тестировании модель показала довольно неплохие результаты при восстановлении данных за последние 30 итераций.


      Ссылки

      1. Нейросети — это просто (Часть 4): Рекуррентные сети
      2. Нейросети — это просто (Часть 14): Кластеризация данных
      3. Нейросети — это просто (Часть 15): Кластеризации данных средствами MQL5
      4. Нейросети — это просто (Часть 16): Практическое использование кластеризации
      5. Нейросети — это просто (Часть 17): Понижение размерности
      6. Нейросети — это просто (Часть 18): Ассоциативные правила
      7. Нейросети — это просто (Часть 19): Ассоциативные правила средствами MQL5
      8. Нейросети — это просто (Часть 20): Автоэнкодеры
      9. Нейросети — это просто (Часть 21): Вариационные автоэнкодеры (VAE)
      10. Unsupervised Learning of Video Representations using LSTMs
      11. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation

      Программы, используемые в статье

      # Имя Тип Описание
      1 rnn_vae.mq5 Советник   Советник обучения рекуррентного автоэнкодера
      2 VAE.mqh Библиотека класса Библиотека класса латентного слоя вариационного автоэнкодера
      3 NeuroNet.mqh Библиотека класса Библиотека классов для создания нейронной сети
      4 NeuroNet.cl Библиотека Библиотека кода программы OpenCL

      …


      Прикрепленные файлы |
      Загрузить ZIP
      MQL5.zip (68.41 KB)
      Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

      Другие статьи автора

      Перейти к обсуждению на форуме трейдеров
      Индикатор CCI. Три шага трансформации Индикатор CCI. Три шага трансформации
      В этой статье мы попробуем внести дополнительные изменения в CCI. Эти изменения коснутся самой логики работы этого индикатора. Вплоть до того, что мы сможем увидеть этот индикатор в главном окне графика.
      Разработка торгового советника с нуля (Часть 21): Новая система ордеров (IV) Разработка торгового советника с нуля (Часть 21): Новая система ордеров (IV)
      Наконец-то визуальная система заработает... хотя пока не до конца. Здесь мы закончим вносить основные изменения, которых будет не мало, но они все необходимы, и вся работа будет достаточно интересной.
      DoEasy. Элементы управления (Часть 13): Оптимизация взаимодействия WinForms-объектов с мышкой, начало разработки WinForms-объекта TabControl DoEasy. Элементы управления (Часть 13): Оптимизация взаимодействия WinForms-объектов с мышкой, начало разработки WinForms-объекта TabControl
      В статье исправим и оптимизируем обработку внешнего вида WinForms-объектов после увода курсора мышки с объекта и начнём разработку WinForms-объекта TabControl.
      Разработка торговой системы на основе индикатора Накопления/Распределения - Accumulation/Distribution Разработка торговой системы на основе индикатора Накопления/Распределения - Accumulation/Distribution
      Представляю вашему вниманию новую статью из серии, в которой мы учимся создавать торговые системы на основе популярных технических индикаторов. В этой статье мы будем изучать индикатор Накопления/Распределения (Accumulation/Distribution, A/D). Также мы разработаем торговую систему на языке MQL5 для работы в платформе MetaTrader 5, используя несколько простых стратегий.