Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
E por quanto tempo essa "ficção-científica" demonstrativa vai continuar?
Onde está o acorde final?
Um final de afirmação de vida!
;)
Parece-me que mesmo com a equação cúbica, a aproximação ainda será áspera em t elevada. E você vai se cansar de mexer na fórmula de Cardano ou Viet, Sergey...
O que eu fiz: decompus (1+q-k)^t = (1+epsilon)^t para a terceira potência. Suponha q = 0,01 e, portanto, epsilon <~ 0,01.
Suponha que t=50. Depois na calculadora, (1+0,01)^50 = 1,645. Aproximação binomial até o 3º grau: (1+0.01)^50 ~ 1 + 50*0.01 + 50*49/2*0.01^2 + 50*49*48/6*0.01^3 = 1 + 0.5 + 0.1225 + 0.0196 = 1.6421. Bem, sim, isso é bastante preciso.
Mas aqui, digamos, em t=100 (pouco mais de 8 anos) o resultado exato é 2,7048... (quase um número e, a propósito). A aproximação binomial ao 3º grau nos dá 1 + 100*0,01 + 100*99/2*0,01^2 + 100*99*98/6*0,01^3 = 1 + 1 + 1 + 0,495 + 0,1617 = 2,6567. Já não é muito preciso, e com o aumento do erro o erro vai aumentar.
Em resumo, em geral, qualquer truncagem binomial começa a dar um erro sistemático. Parece-me que faz sentido fazer um movimento e recusar expansões binomiais e simplesmente trabalhar pelo método de Newton. As aproximações consecutivas sob certas condições convergem para um valor exato muito rapidamente e podem ser calculadas da seguinte forma (equação f(x)=0)
x(n+1) = x(n) - f(x(n))/f'(x(n))
Como nosso f é o primeiro derivado do valor do saque, teremos que encontrar seu segundo derivado. Não deve haver nenhum problema técnico, embora a fórmula seja incômoda. Publicá-lo-ei um pouco mais tarde.
2 avtomat: Não me importo se você me cortar, mas não vejo nenhuma conexão entre sua função de malha e a pequenez do epsilon (esta variável é contínua em princípio). Você pode finalmente me mostrar a fórmula que resolve seu ACS? :) Estou falando da fórmula correspondente àquela dada pelo Neutron na página anterior.
Deixe-me ter sua energia em minha bateria. Mmm....
Se você não tem nada especial a fazer, e quer aplicar sua energia mental em algo muito, você pode beneficiar a sociedade ao reescrever as transformações Hilbert-Huang de C++ para MQL4/MQL5. O código está anexado.
Certo, algo surgiu e desapareceu novamente. OK, ainda estou resolvendo com as tangentes de Newton. E eu não quero saber de todas as ACS e anuidades :)
Estou esperando pelo ACCS e por você. Então eu vou descobrir...
;)
falso início - precisamos avaliar o componente comercial.
Caso contrário, vamos ficar sentados de novo?
DDD
https://ru.wikipedia.org/wiki/%D0%90%D0%BD%D0%BD%D1%83%D0%B8%D1%82%D0%B5%D1%82 - não muito claro, mas gostei muito da expressão 'annuity postnumerando'.
Mais ou menos o mesmo que um broche todas as noites :)
Alexei observou, com razão, a concepção errada de uma proporção constante de "seus-outros".
Mas, além disso, como de costume, atingiu um beco sem saída otimista.
Portanto.
Se alguém realmente precisa de uma solução - eu exponho minha visão. (farto do ASUTP com Arquimedes em suas banheiras esperando;)
Primeiro de tudo, a própria possibilidade de aplicar a técnica de não retirar todos os juros acumulados deve ser decidida.
É fácil entender que, para fazê-lo, o período até o final do prazo do depósito deve ser estritamente maior do que
Vamos tomar o resultado como L
além disso, deduziu-se simplesmente (tendo em mente o tamanho máximo de área/depósito de crescimento "frutífero" -;)Sp é definido como uma linha reta -
No final, temos a retirada máxima. Sr é uma fração do acúmulo...
gráfico de seu comportamento.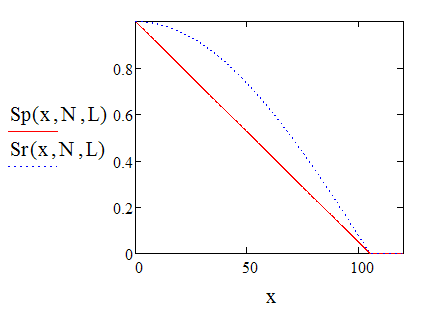
É fácil de contar e usar.
exemplos para - Do=100, N=12*10 A STAFCA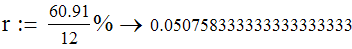
E a anuidade é meu tema, e se você ainda tentar derivar sua fórmula você mesmo.
Observe que B é o tamanho da retirada dos juros acumulados do depósito, inclusive se N for menor do que L.
;)
Observo que o último desenho é "conceitual".
COMO, para entender a idéia de prova.
Qualquer pessoa pode construir uma correta e ficar maravilhada.
;)
O que é k, digamos, quando q=0,01 (1% por mês) e t=80?
Francamente falando, seus cosines estão tensos, Mikhail Andreevich. Se eu não estivesse familiarizado com a fórmula do Black-Scholes, teria perdido a cabeça.
O que é k para, digamos, q=0,01 (1% por mês) e t=80?
Francamente falando, seus cosines estão tensos, Mikhail Andreevich. Se eu não estivesse familiarizado com a fórmula de Black-Scholes, teria perdido a cabeça.
substituir por seno...
D
:)