Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
É tranquilo, ou eu não tenho tempo para isso :)
Acrescentei aí as condições do problema.
Vamos resolver isso a partir daqui.
É isso mesmo. A seguir...
Ou a relação é negativa? - Aumentar os saques no bolso - diminui automaticamente o crescimento do depósito.
nas condições dadas -- exatamente positivo!
Você está se confundindo... Desde que façamos a análise sem embolsar, ou seja, o que constitui tal sistema!
E quanto ao crescimento exponencial, assumi que você estabeleceu essa condição a priori.
Bem, tanto faz. Que seja negativo e severo - não o ponto.
O que há de novo em sua declaração? Nós temos: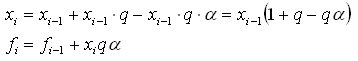
Substituir qa por k e chegamos às mesmas equações que eu tenho:
Com os mesmos problemas.
.
Em nosso caso particular G(s)=0
e as equações são simplificadas por
Agora, aplicando a transformada Laplace inversa, obtemos o resultado:
.
aqui temos o expoente como resultado, não como destino.
.
É isso aí - é claro como o sistema se comporta.
Agora podemos continuar a considerar a segunda parte do problema - ligar a válvula e separar o fluxo.
.
zy.
Chegarei a isso hoje, mas um pouco mais tarde...
P.S. Caso alguém esteja interessado, aqui estão os dados do censo global da Goskomstat para toda a história da humanidade:
Ano milhão de pessoas.
Tive que logaritmo duas vezes para obter este gráfico, mas mesmo assim o crescimento é mais rápido do que uma linha reta. Isto significa que a relação é ainda mais rápida do que exp(exp(t))
Tive que logaritmo duas vezes para obter este gráfico, mas mesmo assim o crescimento é mais rápido do que em linha reta. Isto significa que a dependência é ainda mais rápida do que exp(exp(t))
Sim, a correlação é interessante.
Nos anos 90, o S.P. Kapitsa (aquele que hospeda o espetáculo "Obvious incredible") chegou até nós com um relatório sobre a população da Terra. É interessante que de acordo com seu modelo, que naquela época se encaixava bem nos dados históricos, dN/dt=N^2 e previa um crescimento explosivo da população em 2025 (a chamada catástrofe malthusiana, se não estou enganado). Em geral, para preencher a condição da difurcação acima, é necessário que toda mulher em idade reprodutiva dê à luz um filho de todo homem :-) É sob estas condições que a igualdade da taxa de crescimento para o quadrado da população total seria cumprida. O que parece uma loucura. Então percebi que era uma conseqüência da adequação do modelo aos dados disponíveis. E se você não levar os dados antes de 1945. E se você não levar os dados antes de 1945 (onde você pode ver um pico de natalidade), mas trabalhar em um período mais ou menos calmo de 1945 até agora, então não há nenhuma catástrofe:
Além disso, pode-se ver que a população global está tendendo assimmptoticamente para um nível de equilíbrio de 11 bilhões e alcançará esse nível em cerca de 100 anos.
Ela tem que ser igualada a zero e resolvida com respeito a k.