[Arquivo!] Pura matemática, física, química, etc.: problemas de treinamento do cérebro não relacionados ao comércio de qualquer forma - página 14
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Какие это такие запросы? Вы свой запрос перечитайте, запрос так запрос, - я на первом предложении то застрял, а развитие мысли "какие после каких бывают" добил меня окончательно.
PS: Жаль, что у Вас нет компаса. Хорошая штука - стороны света разные там показывает, направления всякие ...
Bem, não tenho nada a dizer, infelizmente. :(
Ну мне сказать тут нечего, увы. :(
sobre a bússola? - É uma piada, pensei que se encaixaria em seu "psicótipo". :о)
Алексей, тебя мое решение устраивает ?
Думаешь для 7-го это слишком круто (не общий, а частный случай 25 одноклассников) ?
Sim, é um pouco íngreme para um 7. Mas é elementar, o que é bom.
Yurixx escreveu(a) >> Dois elementos devem ter os mesmos valores.
Não é difícil verificar que quando N=26 (ou seja, não há nenhum aluno com zero conexões na classe), este número repetido = 13.
A única coisa que eu não entendo é por que 13 e não 14 ou 2. Você e seu procedimento de partição sequencial fizeram meu cérebro amolecer - mas talvez seja aí que você deva procurar uma explicação do porquê de ser 13 :)
Você usou o princípio de Dirichlet, a propósito, sem nomeá-lo.
А почему так?
boa pergunta)
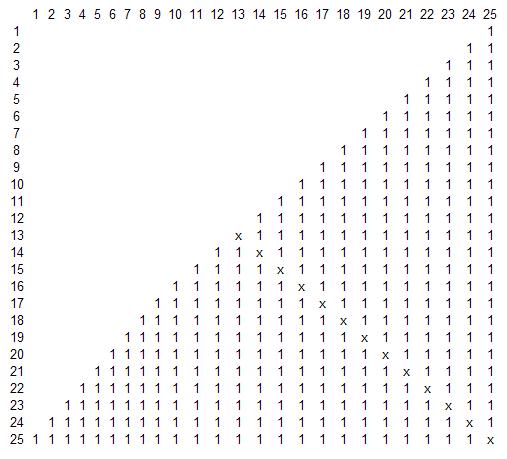
a imagem é (de 1 a 25)
diagonal xxx, ninguém é amigo de si mesmo, é necessário fazer isso Petya e por isso é óbvio treze vezes))))
no caso de zero a 24, você pode ignorar um colega de classe e obter um quadrado de 24*24 e 12 X's.
No caso de um quadrado de tamanho ímpar, a diagonal = (N+1)/2, no caso de um quadrado de tamanho par N/2.
Você pode pensar nisso como a diferença de amizades) na classe com e sem Petya.
Não soa como uma prova rigorosa. É mais uma ilustração que aponta para os dedos, sem nenhuma razão clara para exatamente 12 ou 13. Vamos pensar sobre isso.
A única coisa que eu não entendo é por que 13 e não 14 ou 2. Você e seu procedimento de partição seqüencial amoleceram minha mente - mas talvez seja aí que você deva procurar uma explicação do porquê de ser 13 :)
Você usou o princípio Dirichlet, a propósito, sem nomeá-lo.
A questão é que sob esta divisão (e obedece apenas a um princípio - todos têm um número diferente de amigos e, portanto, é bastante geral) Petya não participa de forma alguma. Ele é um dos 26 estudantes, absolutamente igual aos outros. Como resultado, acontece que todos não podem ter um número diferente de amigos - a série de 1 a N-1 não pode ser numerada consecutivamente N números diferentes (está na prova final). Portanto, dois estudantes devem ter o mesmo número de amigos. E estes dois estudantes estão ao lado um do outro no centro da fila. Então, acontece que Petya deve ser um desses dois. Somente neste caso, todos os outros têm um número diferente de amigos. Quaisquer outras marcações não podem satisfazer esta condição.
Se você tentar particionar à mão no centro, você verá por si mesmo.
A tabela do Swan ilustra isso.
Espero ter entendido corretamente sua pergunta.
Acho que não usei o princípio de Dirichlet, mas ofereci uma prova elementar de seu caso especial.
Eu pessoalmente adorei.
É elegante.
Isso me fez lembrar da fábula sobre a pequena e ágil Gauss e o professor que deu à classe a tarefa de adicionar números de 1 a 99 e que ia decolar por um tempo - enquanto as crianças estavam adicionando.
Eles já conheciam a multiplicação, mas a repetição é a mãe do aprendizado.
Gauss enganou o professor - a resposta veio logo em seguida.
;)
Swetten у нас самая дружелюбная.
:)
В коллективе из N сотрудников не может быть ситуации когда у каждого разное количество друзей
А вот если добавить - "у двух возможно одинаковое количество друзей" тогда нет проблем
Остается обозвать Петей одного из этих двух
Sim, isso é quase certo.
Se você ler o problema legalmente, então Peter PODE ter o mesmo número de amigos que um dos outros.
Eu lhe disse - este problema é incorreto - por QUALQUER leitura das condições. Provavelmente posso provar isso, e de várias maneiras. Mas eu ainda não......