Hibridização de algoritmos populacionais. Estruturas sequenciais e paralelas

Conteúdo

1. Introdução
2. Experimentando com GWO e COA
3. Experimentando com ESG e SDSm
4. Conclusões

1. Introdução

Vamos considerar três opções principais para hibridizar algoritmos de otimização:

1. Misturando estratégias de busca de algoritmos em uma só. Cada algoritmo possui seu próprio conjunto de habilidades e capacidades. Misturar suas estruturas lógicas proporciona uma variedade de propriedades na busca comum pelo sucesso. Este é um verdadeiro baile de estilos, onde cada passo complementa e aprimora o movimento geral. Um exemplo dessa abordagem é a Otimização por Forrageamento Bacteriano combinada com o algoritmo genético discutido em um dos artigos anteriores.

2. Operação consistente de cada um dos algoritmos dividindo as iterações em trabalho parcial de um e o trabalho final do outro, como passar um bastão. Algoritmos são como equipes esportivas, cada uma especializada em seu próprio estágio da corrida. Passar o bastão entre eles implica na transferência de conhecimento e resultados, criando uma transição suave e eficiente de um estágio para o próximo, como a harmonia de uma equipe bem coordenada, mantendo o número total de iterações inalterado.

3. A operação paralela de cada algoritmo com a subsequente combinação dos melhores resultados únicos se assemelha à criatividade coletiva, onde cada algoritmo é um artista, colocando sua energia única na tela comum do mundo. Em cada iteração, os melhores resultados são combinados. Cada pincelada complementa e expande a compreensão do problema em estudo, criando uma visão comum da solução ideal.

Essas opções de hibridização algorítmica oferecem oportunidades significativas para combinações criativas de diferentes abordagens e estratégias, levando a novas descobertas e melhorias na otimização. Assim como no mundo da arte, uma variedade de estilos e técnicas inspira a criação de obras únicas, a combinação harmoniosa de diferentes algoritmos pode levar a resultados ótimos e à exploração eficiente de problemas complexos.

No mundo da busca por soluções ideais, onde cada passo no espaço de opções é importante, é fundamental não apenas buscar, mas também encontrar com confiança para alcançar o resultado desejado. O estudo experimental que realizamos em um artigo anterior no campo dos algoritmos de otimização populacional, onde forçamos os algoritmos a serem posicionados no ponto mínimo global para alcançar o ponto máximo global, revelou um aspecto importante: a dependência do sucesso em relação às condições iniciais. Alguns algoritmos tiveram dificuldade em sair do ponto mínimo, perdendo eficiência, enquanto outros se destacaram como exemplos de estabilidade universal com pouca dependência da posição inicial. Alguns deles exploraram o espaço com sucesso no início do processo, enquanto outros tentaram melhorar os resultados nas etapas posteriores. Essas características únicas de cada algoritmo podem ser usadas com sucesso, realçando seus aspectos positivos e reduzindo suas desvantagens. Esperamos que a combinação de diferentes estratégias possa levar a métodos mais eficientes que possam explorar o espaço com sucesso e melhorar os resultados em diferentes estágios do trabalho. É importante acrescentar que, graças à padronização, a hibridização de algoritmos tornou-se mais acessível. Agora, todos os algoritmos populacionais foram reunidos em uma única classe, o que abre portas para combinações criativas e possibilidades completamente novas.

2. Experimentando com GWO e COA

Para este experimento, usaremos dois algoritmos que possuem diferentes desempenhos e características: GWO e COAm. Enquanto o GWO está localizado no final da tabela de classificação, o COAm está localizado no meio. Vamos tentar descobrir quais resultados podem ser alcançados usando suas combinações em operação sequencial e paralela. Não consideraremos a mistura de elementos lógicos das estratégias de busca neste artigo, pois isso é muito específico para cada combinação de algoritmos e não pode ser considerado dentro do escopo de um único artigo.

Grey Wolf Optimizer (GWO) é um algoritmo metaheurístico estocástico baseado na simulação da caça de uma matilha de lobos cinzentos.
Características principais do algoritmo GWO:

• Simulação do comportamento da matilha. O algoritmo usa uma estrutura hierárquica de uma matilha de lobos, onde cada lobo desempenha um papel diferente (alfa, beta, delta, ômega).
  
• Busca pelo máximo global. Os lobos alfa, beta e delta são considerados os mais adaptáveis e estão mais próximos da presa, enquanto os outros lobos tendem a se aproximar deles. O GWO avança rapidamente em direção a um potencial extremo global.
  
• Adaptabilidade. À medida que o algoritmo trabalha, os lobos estão constantemente se rearranjando, o que lhes permite se adaptar a condições em mudança.
  

O Algoritmo de Otimização Cuco (COAm) é um dos mais recentes algoritmos heurísticos inspirados na natureza. Ele é baseado no parasitismo de algumas espécies de cuco.
Características principais do algoritmo COAm:

• Simulação do comportamento do cuco. O algoritmo usa uma estratégia de reprodução de cuco, onde o cuco coloca seus ovos nos ninhos de outras aves.
• Busca pelo máximo global. Os ovos no ninho são interpretados como possíveis soluções para o problema de otimização, e o ovo do cuco representa a nova solução.
  
• Adaptabilidade. Se o ovo do cuco for de qualidade superior ao ovo original, ele o substituirá. Caso contrário, o ovo original permanecerá no ninho.

Assim, hibridizar esses algoritmos presumivelmente permitirá utilizar suas vantagens combinadas para resolver problemas de otimização de maneira mais eficiente. A Figura 1 mostra um diagrama sequencial da operação do GWO e COAm. Após a conclusão da primeira etapa, quando algumas iterações são alocadas para o GWO, os estados dos agentes de um algoritmo são transferidos para o outro. Cada um dos agentes renasce em uma nova espécie (neste caso, o lobo se transforma em um cuco) onde a posição dos indivíduos é mantida na população.

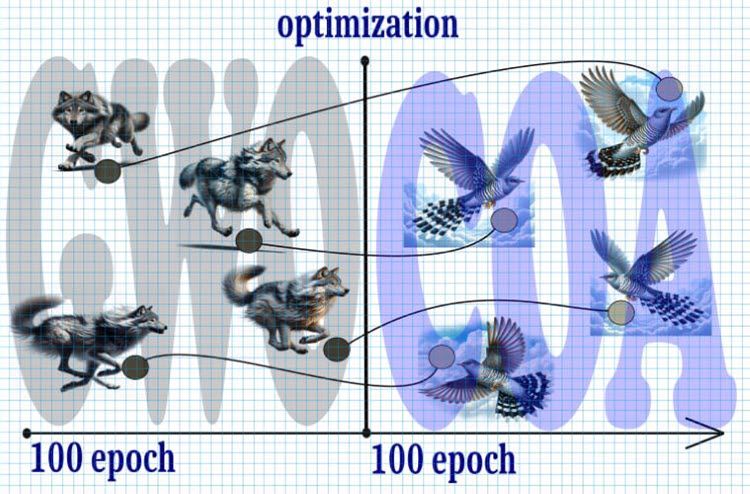
Figura 1. Algoritmo híbrido, GWO+COA

Vamos dar uma olhada no curso provável dos eventos:

1. Início:
- Começamos com 10.000 iterações, que é um recurso limitado, portanto, cada iteração é crucial para alcançar a solução ideal.
2. Passo 1 (0—5000 iterações):
- Divida o número total de iterações pela metade e comece com o algoritmo GWO.
- Devido à rápida dispersão dos lobos pelo espaço de busca, eles rapidamente convergem para um potencial extremo global no meio do período.
3. Passo 2 (5000 — 10000 iterações):
- Após as primeiras 5000 iterações, adotamos a posição dos lobos para a posição dos cucos nesses pontos.
- A busca do cuco com o voo de Levy recebe a vez para refinar ainda mais o extremo.
4. Resultado:
- Espera-se que, como resultado dessa combinação dos algoritmos GWO e busca do cuco com voo de Levy, consigamos alcançar um extremo global mais preciso e estável em um número limitado de iterações.

Assim, o uso dessa estratégia permitirá otimizar a busca por um extremo global em um número limitado de iterações, garantindo um equilíbrio entre a velocidade de convergência e a precisão do resultado.

Declare a classe "C_AO_GWO_COAm", que é uma herdeira da classe "C_AO". O construtor da classe define valores padrão para parâmetros de otimização, como o tamanho da população "popSize" e a "proporção" entre os algoritmos GWO e COAm. A classe permitirá o uso da operação sequencial de dois algoritmos, enquanto seu manuseio permanecerá o mesmo de sempre, permitindo-nos usar nosso banco de testes sem alterações.

A classe também define os métodos para definir parâmetros (SetParams), inicializar a otimização (Init), mover (Moving) e atualizar (Revision) a solução global, e inserir (Injection) valores de coordenadas nos agentes.

Variáveis importantes na classe incluem "ratio" (a proporção entre GWO e COAm), bem como objetos de classe C_AO_GWO e C_AO_COAm para implementar o Grey Wolf Optimizer e o Algoritmo de Otimização Cuco, respectivamente.

A classe também possui variáveis para rastrear o número de épocas e a época atual para cada um dos algoritmos (GWO e COAm).

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GWO_COAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_GWO_COAm () { }
  C_AO_GWO_COAm ()
  {
    ao_name = "GWO_COAm";
    ao_desc = "Grey Wolf Optimizer and Cuckoo Optimization Algorithm M";

    popSize = 50;    //population size
    ratio   = 0.5;   //the ratio of GWO and COAm

    ArrayResize (params, 2);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "ratio";   params [1].val = ratio;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    ratio   = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double ratio;  //the ratio of GWO and COAm

  private: //-------------------------------------------------------------------
  C_AO_GWO  AO1;
  C_AO_COAm AO2;

  int epochCount;
  int epochNow;

  int epochGWO;
  int epochCOAm;
};
//——————————————————————————————————————————————————————————————————————————————

O método Init na classe C_AO_GWO_COAm é usado para inicializar o processo de otimização. É aqui que são definidos os valores iniciais, criados os agentes, e definidos os parâmetros de inicialização para os algoritmos GWO e COAm.

1. O sucesso da inicialização padrão é verificado usando o método StandardInit, que usa os parâmetros passados para definir o intervalo mínimo e máximo de busca.
2. O número de épocas para cada um dos algoritmos GWO e COAm é calculado com base na "ratio" e no número total de épocas (epochCount).
3. Os parâmetros para os algoritmos GWO e COAm são definidos e inicializados usando os métodos SetParams e Init.
4. O método retorna "true" se a inicialização for bem-sucedida.

O método fornece a configuração inicial e a inicialização dos algoritmos GWO e COAm para otimizar o problema com os parâmetros e restrições dados.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_GWO_COAm::Init (const double &rangeMinP  [], //minimum search range
                          const double &rangeMaxP  [], //maximum search range
                          const double &rangeStepP [], //step search
                          const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochCount   = epochsP;
  epochNow     = 0;

  epochGWO  = int(epochCount *ratio);
  epochCOAm = epochCount - epochGWO;

  AO1.params [0].val = popSize;
  AO2.params [0].val = popSize;

  AO1.SetParams ();
  AO2.SetParams ();

  AO1.Init (rangeMinP, rangeMaxP, rangeStepP, epochGWO);
  AO2.Init (rangeMinP, rangeMaxP, rangeStepP, epochCOAm);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O valor da variável "epochNow" aumenta em um no código do método Moving da classe C_AO_GWO_COAm. O contador "epochNow" é usado para determinar as etapas em que o GWO e, posteriormente, o COAm operam, respectivamente.

Se "epochNow" for menor que "epochGWO", então o método Moving é chamado para o objeto AO1 (GWO), após o qual os elementos do array de agentes "AO1.a" são copiados para o array de agentes "a".

Se "epochNow" for igual a "epochGWO", o método Moving é chamado no objeto "AO2" (COAm), e os valores do array "AO1.a" são então inseridos nos elementos correspondentes do array "AO2.a", ou seja, essa é a transformação dos lobos em cucos. Finalmente, todos os elementos do array "AO2.a" são copiados para o array "a" para acessar os agentes "a" no programa em execução.

Esse método garante que os agentes se movam sequencialmente em cada época de otimização, de acordo com os algoritmos GWO e COAm selecionados.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  epochNow++;

  if (epochNow < epochGWO)
  {
    AO1.Moving ();
    for (int i = 0; i < popSize; i++)
    {
      a [i] = AO1.a [i];
    }
    return;
  }

  AO2.Moving ();

  if (epochNow == epochGWO)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        AO2.Injection (i, c, AO1.a [i].c [c]);
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    a [i] = AO2.a [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método Revision transmite o valor de aptidão calculado dos agentes para os agentes correspondentes dos algoritmos.

Dependendo do valor das variáveis "epochNow" e "epochGWO", as seguintes ações são realizadas para os algoritmos GWO ou COAm:

1. Copiar o valor de aptidão para os agentes.
2. Executar o método Revision.
3. Executar uma atualização da solução global.
   

Assim, o método implementa a lógica de atualização da solução global com a solução dos algoritmos GWO e COAm, dependendo do estágio atual de execução dos algoritmos correspondentes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  if (epochNow < epochGWO)
  {
    for (int i = 0; i < popSize; i++) AO1.a [i].f = a [i].f;

    AO1.Revision ();

    if (AO1.fB > fB)
    {
      fB = AO1.fB;
      ArrayCopy (cB, AO1.cB, 0, 0, WHOLE_ARRAY);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++) AO2.a [i].f = a [i].f;

    AO2.Revision ();

    if (AO2.fB > fB)
    {
      fB = AO2.fB;
      ArrayCopy (cB, AO2.cB, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

A visualização da operação do algoritmo híbrido destaca o seguinte fenômeno: o GWO frequentemente fica preso em extremos locais, interrompendo prematuramente seu rápido movimento. Em contraste, o algoritmo COA deixa para trás uma variedade de resultados criando uma gama, às vezes impressionante, de pontos finais.

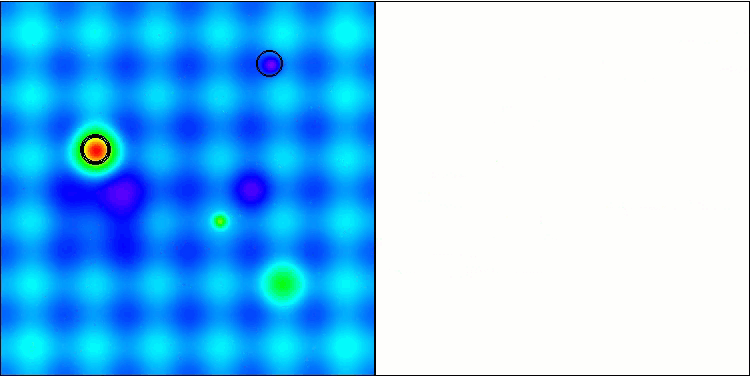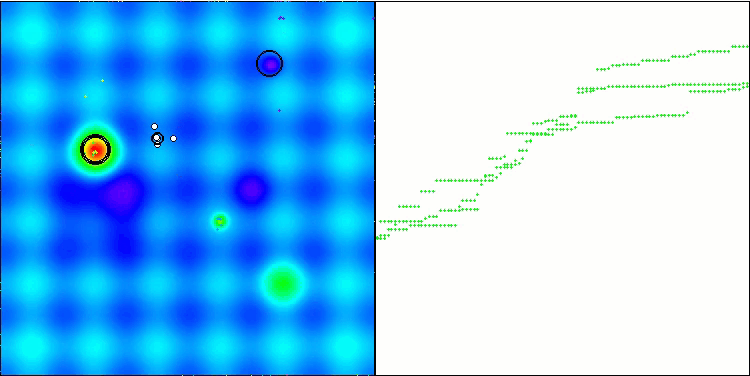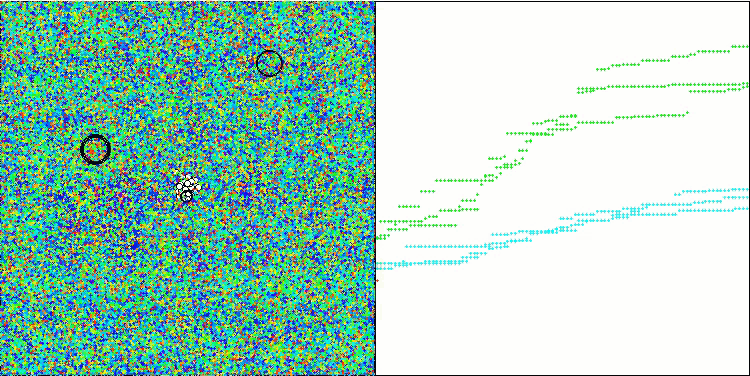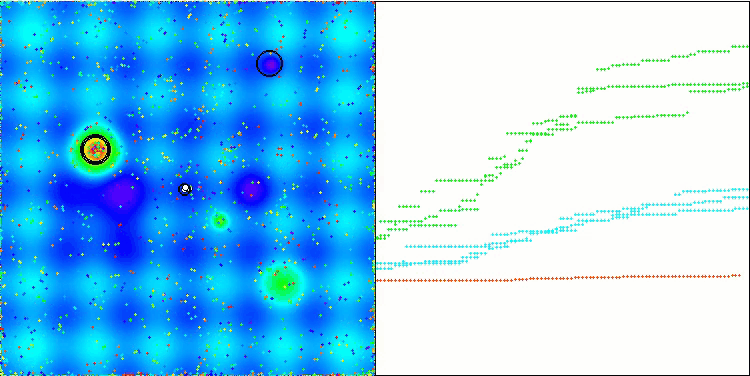
GWO-COAm na função de teste Hilly

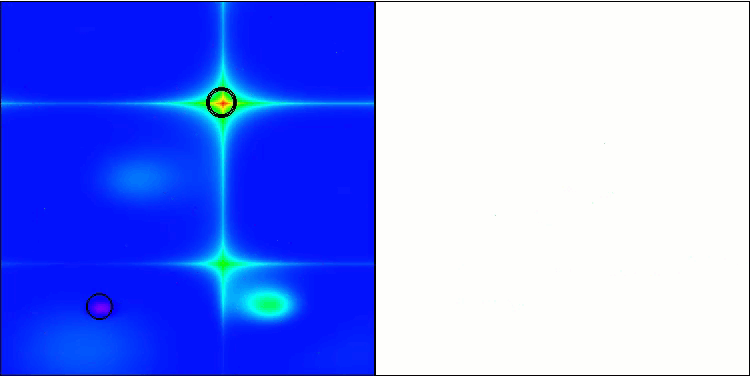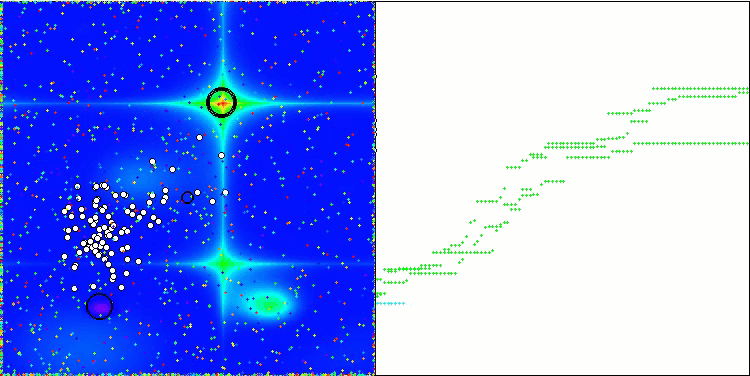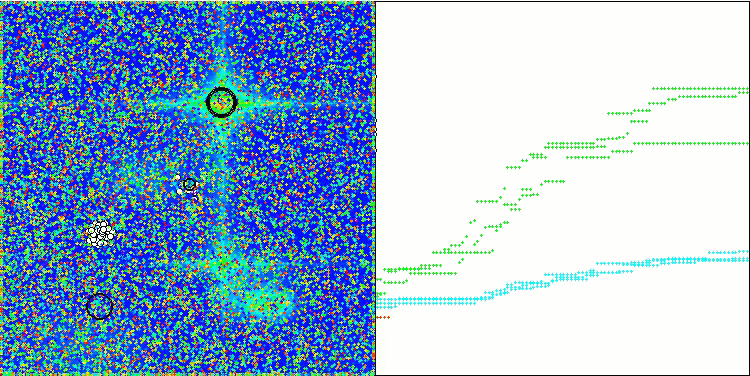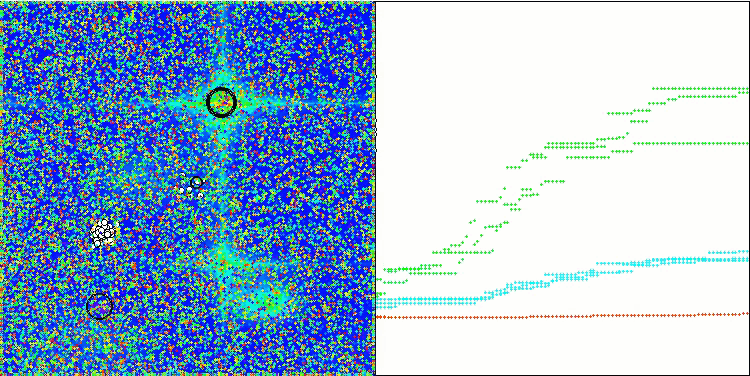
GWO-COAm na função de teste Forest

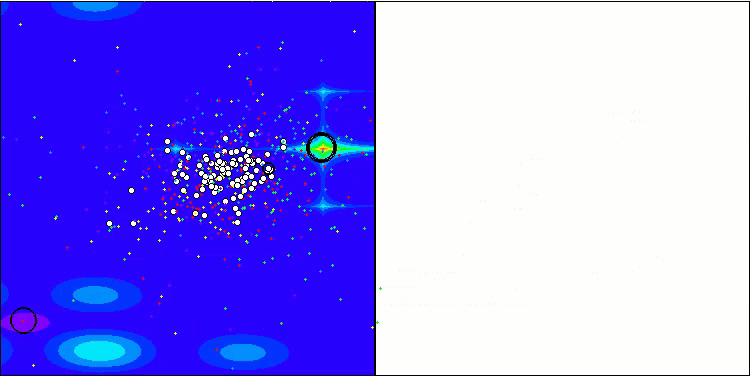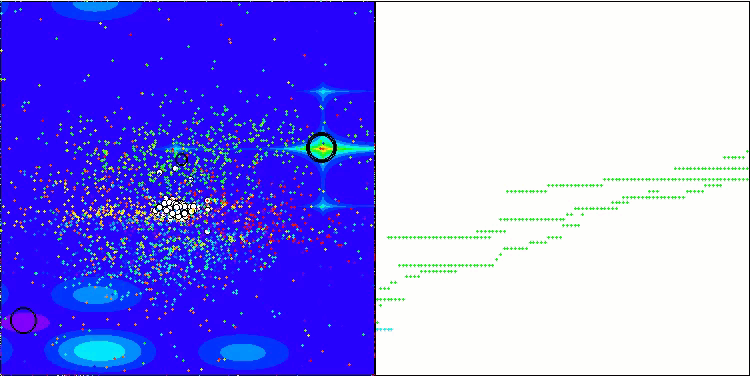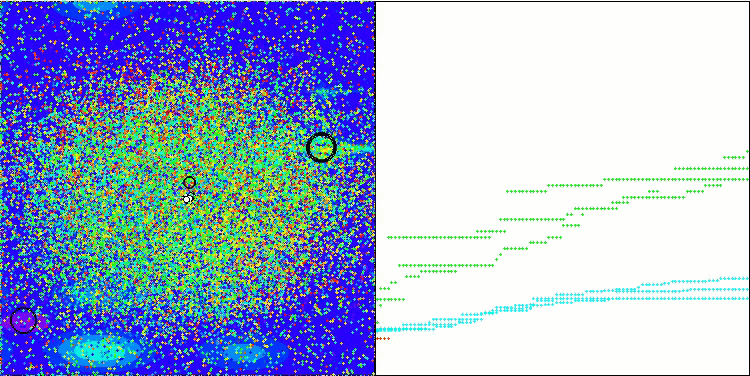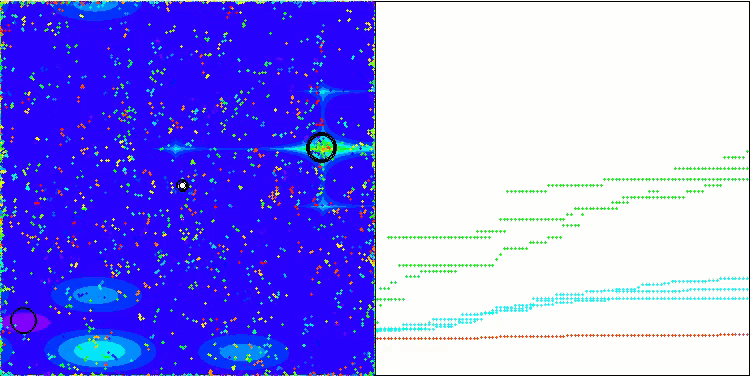
GWO-COAm na função de teste Megacity

Então, conduzimos um experimento tentando criar um algoritmo híbrido combinando os algoritmos GWO e COAm sequencialmente. No entanto, isso não levou aos resultados desejados (melhorando o desempenho do melhor). O GWO frequentemente fica preso em máximos locais e para de se mover, enquanto o algoritmo COAm não conseguiu pegar a deixa e é caracterizado por uma grande dispersão nos resultados finais, dependendo do número de execuções experimentais.

Resultados do banco de testes GWO-COAm (estrutura sequencial):

GWO_COAm|Grey Wolf Optimizer e Algoritmo de Otimização Cuco M|50.0|0.3|
=============================
5 Hilly's; Execuções da função: 10000; resultado: 0.729041499138184
25 Hilly's; Execuções da função: 10000; resultado: 0.4465971838522985
500 Hilly's; Execuções da função: 10000; resultado: 0.2685674823439256
=============================
5 Forest's; Execuções da função: 10000; resultado: 0.6963174902735325
25 Forest's; Execuções da função: 10000; resultado: 0.347940898514357
500 Forest's; Execuções da função: 10000; resultado: 0.16776831572853218
=============================
5 Megacity's; Execuções da função: 10000; resultado: 0.5492307692307692
25 Megacity's; Execuções da função: 10000; resultado: 0.2464615384615385
500 Megacity's; Execuções da função: 10000; resultado: 0.10724615384615484
=============================
Pontuação total: 3.55917 (39.55%)

O resultado é comparável ao da operação separada do COAm. Há uma melhora, mas, infelizmente, é insignificante. No entanto, em execuções independentes individuais, o COAm às vezes produz resultados comparáveis.

Vamos tentar criar um híbrido que combine o trabalho paralelo com a troca, a cada iteração, das melhores posições dos agentes de dois algoritmos que não apenas trabalharão de forma independente, mas também trocarão as melhores soluções entre si para um objetivo comum.

Agora vamos tentar usar a operação paralela dos algoritmos GWO e COAm. Para isso, praticamente não precisamos alterar a classe do algoritmo conjunto. Fornecerei apenas o código dos métodos que exigem mudanças significativas.

Ao contrário da estrutura sequencial, aqui lançamos os métodos Moving de ambos os algoritmos ao mesmo tempo. Após isso, copiamos os agentes desses algoritmos para os agentes da classe combinada para o cálculo subsequente da função de aptidão. Assim, o método combina os dados de dois objetos "AO1" e "AO2" no array de objetos atuais "a".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  AO1.Moving ();
  AO2.Moving ();

  int cnt = 0;
  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO1.a [i];
    cnt++;
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO2.a [i];
    cnt++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

As diferenças do método Moving para a estrutura de operação paralela são as seguintes: após transferir os valores de aptidão para os agentes dos objetos "AO1" e "AO2", executar seus métodos Revision e atualizar a solução global, os agentes são copiados de um algoritmo para o outro em pares. Isso significa que os dois melhores agentes são trocados entre os algoritmos, o que ajuda ambos os algoritmos a enriquecer as melhores características um do outro e melhorar seu desempenho na solução de problemas. Essa abordagem permite que as melhores soluções alcançadas por cada algoritmo sejam compartilhadas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  int cnt = 0;

  for (int i = 0; i < popSize / 2; i++)
  {
    AO1.a [i].f = a [cnt].f;
    cnt++;

    if (AO1.a [i].f > fB)
    {
      fB = AO1.a [i].f;
      ArrayCopy (cB, AO1.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    AO2.a [i].f = a [cnt].f;
    cnt++;

    if (AO2.a [i].f > fB)
    {
      fB = AO2.a [i].f;
      ArrayCopy (cB, AO2.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  AO1.Revision ();
  AO2.Revision ();
  
  S_AO_Agent temp [];
  ArrayResize (temp, popSize / 2);
  
  for (int i = 0; i < 2; i++) temp [i] = AO1.a [i]; 

  for (int i = 0; i < 2; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      AO1.Injection (i, coords - 1, AO2.a [i].c [c]);
      AO2.Injection (i, coords - 1, temp  [i].c [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Resultados do banco de testes GWO-COAm (estrutura paralela):

GWO_COAm|Grey Wolf Optimizer e Algoritmo de Otimização Cuco M|50.0|
=============================
5 Hilly's; Execuções da função: 10000; resultado: 0.6930620289919492
25 Hilly's; Execuções da função: 10000; resultado: 0.4389512737634269
500 Hilly's; Execuções da função: 10000; resultado: 0.26733735583025275
=============================
5 Forest's; Execuções da função: 10000; resultado: 0.6512995888741085
25 Forest's; Execuções da função: 10000; resultado: 0.33119611021722106
500 Forest's; Execuções da função: 10000; resultado: 0.16858175021299981
=============================
5 Megacity's; Execuções da função: 10000; resultado: 0.4615384615384615
25 Megacity's; Execuções da função: 10000; resultado: 0.23015384615384615
500 Megacity's; Execuções da função: 10000; resultado: 0.1059538461538471
=============================
Pontuação total: 3.34807 (37.20%)

Infelizmente, não houve melhorias de desempenho.

3. Experimentando com ESG e SDSm>

Nas opções de hibridização GWO e COAm discutidas acima, foram usados algoritmos de "categorias de peso" diferentes. É razoável usar algoritmos que sejam semelhantes em capacidades para que eles realmente se complementem. Portanto, conduziremos mais dois experimentos usando estruturas sequenciais e paralelas. Para isso, usaremos os algoritmos ESG e SDSm.

Combinar esses dois algoritmos em um híbrido pode criar uma combinação única de aleatoriedade e dinâmica social.

O Stochastic Diffusion Search (SDSm) é um algoritmo de otimização populacional.

As principais características do algoritmo:

• Avaliação parcial das soluções. Os agentes realizam uma avaliação parcial das hipóteses (soluções candidatas ao problema de busca), o que reduz a complexidade computacional do algoritmo.
• Distribuição de soluções promissoras. Os agentes trocam informações sobre as hipóteses por meio de comunicação pessoal direta. Soluções de alta qualidade podem ser identificadas a partir de clusters de agentes com a mesma hipótese.
• Justificativa matemática. O SDSm tem uma base matemática profunda, tornando-o mais confiável e previsível.

O SDSm é um método de otimização evolutiva que combina busca aleatória e difusão para resolver problemas de otimização em espaços de alta dimensionalidade.

A Evolução de Grupos Sociais (ESG) é um algoritmo de otimização de multi-população.

As principais características do algoritmo:

• Grupos sociais. O algoritmo não opera com partículas individuais, mas com grupos sociais unidos pela cooperação e troca de experiências. Cada grupo tem seu próprio centro de decisão e um conjunto de partículas como agentes de otimização.
• Movimento coletivo. As partículas dentro dos grupos sociais interagem e se movem juntas no espaço de parâmetros. Isso permite que os grupos explorem diferentes regiões do espaço de parâmetros e compartilhem informações sobre as melhores soluções encontradas.
• Experiência local e global. Cada grupo social armazena informações sobre a melhor solução dentro dele (experiência local). Há também uma melhor pontuação geral entre todos os grupos (experiência global).

O ESG é uma arquitetura simples com alta convergência e baixos requisitos computacionais.

O código para conduzir experimentos em operação sequencial e paralela é exatamente o mesmo que o acima, exceto que precisamos substituir a declaração dos objetos correspondentes dessas classes em vez de GWO e COAm.

Resultados do banco de testes ESG-SDSm (estrutura sequencial):

ESG_SDSm|Evolução dos Grupos Sociais e Busca de Difusão Estocástica M|200.0|0,5|
=============================
5 Hilly's; Execuções da função: 10000; resultado: 0.9642488921252973
25 Hilly's; Execuções da função: 10000; resultado: 0.7526240638447592
500 Hilly's; Execuções da função: 10000; resultado: 0.2961693434072249
=============================
5 Forest's; Execuções da função: 10000; resultado: 0.9897783503200446
25 Forest's; Execuções da função: 10000; resultado: 0.7608845505131734
500 Forest's; Execuções da função: 10000; resultado: 0.2130287247171918
=============================
5 Megacity's; Execuções da função: 10000; resultado: 0.82
25 Megacity's; Execuções da função: 10000; resultado: 0.5421538461538462
500 Megacity's; Execuções da função: 10000; resultado: 0.11932307692307798
=============================
Pontuação total: 5.45821 (60.65%)

Resultados do teste ESG-SDSm (estrutura paralela):

ESG_SDSm|Evolução dos Grupos Sociais e Busca de Difusão Estocástica M|200.0|
=============================
5 Hilly's; Execuções da função: 10000; resultado: 0.9561232188424761
25 Hilly's; Execuções da função: 10000; resultado: 0.7493199026465321
500 Hilly's; Execuções da função: 10000; resultado: 0.3176797705433513
=============================
5 Forest's; Execuções da função: 10000; resultado: 0.9726744619317564
25 Forest's; Execuções da função: 10000; resultado: 0.7494321306074204
500 Forest's; Execuções da função: 10000; resultado: 0.22498291462144127
=============================
5 Megacity's; Execuções da função: 10000; resultado: 0.836923076923077
25 Megacity's; Execuções da função: 10000; resultado: 0.5261538461538462
500 Megacity's; Execuções da função: 10000; resultado: 0.13435384615384738
=============================
Pontuação total: 5.46764 (60.75%)

Os resultados para as estruturas de hibridização sequencial e paralela acabaram sendo muito próximos, enquadrando-se no erro usual de algoritmos estocásticos. Eles são ligeiramente inferiores aos resultados de operação separada desses algoritmos.

4. Resumo

Os algoritmos considerados neste artigo como componentes para hibridização foram selecionados para cobrir várias posições na tabela de classificação atual e para entender o impacto do desempenho diferente de cada algoritmo no resultado geral. É importante que os algoritmos sejam aproximadamente iguais em capacidade de busca para garantir uma análise equilibrada e uma comparação justa de seu impacto no resultado final?

Neste artigo, consideramos vários algoritmos de otimização como componentes para hibridização. Nosso objetivo é cobrir uma ampla gama de algoritmos que ocupam diferentes posições na tabela de classificação atual para descobrir como o desempenho diferente de cada algoritmo afeta o resultado geral.

Se é importante que os algoritmos sejam aproximadamente iguais em capacidade de busca permanece uma questão em aberto. Isso pode não ser relevante se o objetivo principal for encontrar a melhor solução.

Para os experimentos, escolhemos algoritmos que diferem muito em suas capacidades, como GWO e COA. Esses algoritmos representam duas abordagens diferentes para a otimização, e combiná-los pode nos ensinar lições valiosas. Em contraste, também selecionamos algoritmos que são muito semelhantes em desempenho, como ESG e SDSm.

Abaixo está a tabela de classificação atual dos algoritmos. Ela inclui todos os algoritmos que discutimos e será atualizada à medida que novos dados estiverem disponíveis.

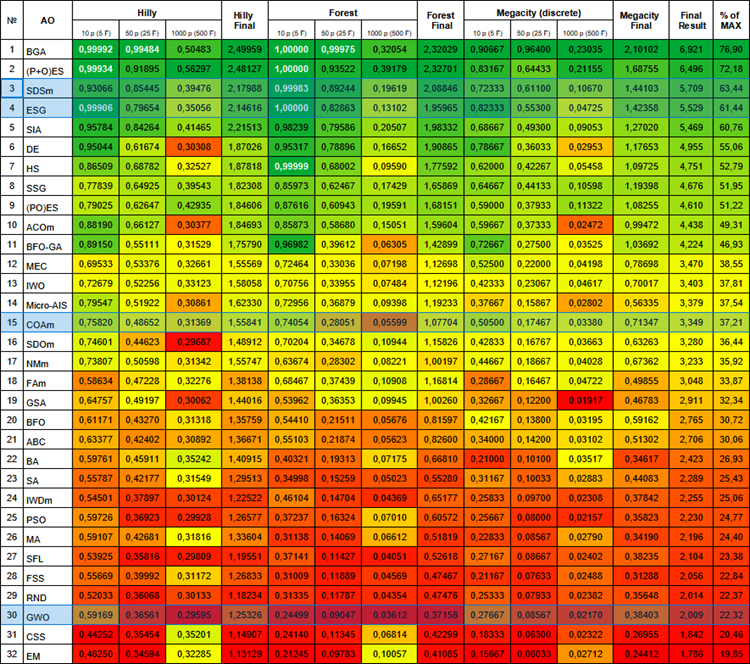
Tabela de classificação de algoritmos populacionais

Ao tentar criar um método híbrido combinando trabalho paralelo e troca das melhores posições dos agentes dos algoritmos ESG e SDSm, assim como na estrutura sequencial, encontramos um fenômeno ambíguo. No decorrer de nossa pesquisa, descobrimos que a combinação dessas duas abordagens não levou a sinergia e aprimoramento, mas a um resultado mediano. É provável que a interação entre essas diferentes estratégias não tenha sido eficiente o suficiente, impedindo a plena integração de seus princípios centrais.

Como resultado dos experimentos, ficou claro que tanto as estruturas de hibridização sequencial quanto as paralelas não levaram aos resultados desejados sob essas condições, destacando a importância da seleção cuidadosa de algoritmos para uma combinação bem-sucedida. É necessário que os algoritmos inicialmente possuam certas qualidades: ou eles buscam bem e são pouco refinados, ou vice-versa. Somente nesse caso os métodos de hibridização podem melhorar o desempenho de ambos os algoritmos. A experiência bem-sucedida de hibridização através da fusão da lógica algorítmica (de acordo com a primeira estrutura) destaca o potencial dessa abordagem, no entanto, ela requer esforço não trivial, intervenção cuidadosa e o desenvolvimento de uma lógica de fusão conjunta para alcançar resultados ideais.

Assim como na natureza, onde a combinação de diferentes espécies pode levar a adaptações únicas, no mundo da otimização, a combinação de algoritmos exige ajustes finos e harmonia. Talvez, sejam nas combinações inesperadas e nas tentativas fracassadas que encontramos as chaves para novas descobertas e melhorias no campo da otimização. Essa experiência destaca a importância da análise cuidadosa e da seleção de algoritmos ao criar métodos de otimização híbridos.

Essa experiência destaca a importância da análise cuidadosa e da seleção de algoritmos ao criar métodos de otimização híbridos. É necessário levar em conta não apenas as características individuais de cada algoritmo, mas também sua interação dentro do contexto de uma tarefa específica para alcançar resultados bem-sucedidos na busca por soluções ótimas.

Tente, experimente, crie e combine. Como sempre, todas as ferramentas e códigos-fonte estão anexados abaixo.