
모집단 최적화 알고리즘: 파티클 스웜(PSO)
이것들은 태양 광선에 떠다니는 뚜렷한 떼를 형성합니다.
또는 뇌운을 따라가세요. 대기가 배출하는 데에서 에너지를 끌어올 수 있습니다.
그러나 위험한 순간, 더 넓게는 존재를 위협하는 갑작스러운 변화의 순간에 그들은 단결합니다...
스타니스와프 렘의 "The Invincible"
콘텐츠
1. 소개
스타니스와프 렘의 멋진 공상과학 베스트셀러 'The Invincible'를 읽어 보신 분들도 꽤 많으실 겁니다. 놀랍게도 '군집(swarm)' 지능에 대한 최초의 설명 중 하나가 바로 이 공상과학 소설의 출간과 함께 탄생했습니다. 스토리는 중앙 집중식 제어 없이 살아남은 로봇에 대한 이야기입니다. 특히 가장 복잡하고 지능적이며 강력한 표본보다는 가장 단순하고 많은 표본이 살아남았습니다.
수천 년에 걸친 네크로 진화 과정에서 이 기계들은 지능과 에너지의 가용성 측면에서 자신들을 능가하는 경쟁자들에 대해 효과적으로 대처하는 방법을 배웠습니다. 그들은 다른 로봇 뿐만 아니라 지구에 존재하는 세계와도 싸워야 했습니다. 이 작품에서 판타지의 요소는 진화와 자연 그 자체와 비교할 수 있습니다.
새들이 무리를 지어 따뜻한 곳으로 이동하는 방법, 꿀벌 떼가 먹이를 생산하는 방법, 개미 군집이 복잡한 구조를 만들면서 생존하는 방법, 물고기가 떼를 지어 행동하는 방법과 그 행동들이 동기화되는 이유 등 사람들은 아주 오래전부터 집단 내 동물들의 행동(소위 군집 행동)에 관해 관심을 가져왔습니다. 잘 조율된 통합 유기체와 같은 패턴을 보이는 사회 안의 개인들의 조직은 알고리즘 최적화 분야에서 새로운 아이디어를 떠오르게 합니다.
군집 지능은 자기 조직화 시스템의 집단 행동의 시뮬레이션을 설명합니다. 이러한 알고리즘은 상당히 많이 있습니다. 1995년 케네디(J.Kennedy)와 에버하트(R.Eberhart)가 작성한 표준 버전에서는 레이놀즈 모델을 단순화하여 이 방법의 기초가 되는 모델을 얻었습니다. 이러한 단순화의 결과 모집단의 뚜렷한 개별 개체가 크기는 없지만 어느 정도 속도를 가진 별도의 개체로 나타나기 시작했습니다.
이는 물질 입자와 극도로 유사하기 때문에 그 결과물인 단순한 물체를 입자라고 지칭하였고 그 집단을 스웜이라고 불렀습니다. 매 순간(각 반복 시)마다 파티클은 공간에서 일정한 위치와 속도 벡터를 갖습니다. 파티클의 각 위치에 대해 목적 함수의 해당 값이 계산되고 이를 기반으로 특정 규칙에 따라 파티클은 검색 공간에서 위치와 속도를 변경합니다. 파티클의 다음 위치를 결정할 때 적합성 함수의 작업에 해당하는 다른 모든 인접 파티클 중에서 가장 좋은 위치에 대한 정보가 고려됩니다.
스웜 알고리즘의 예:
- 파티클 스웜 메서드
- 개미 알고리즘
- 꿀벌 알고리즘
- 인공 면역 시스템
- 회색 늑대 알고리즘
- 박쥐 알고리즘
- 중력 검색 알고리즘
- 이타주의 알고리즘
- 기타 여러 가지
집단 행동 모델링에서 집단 최적화로의 전환은 다음과 같은 생물학적 아이디어에 기반합니다: 유기체는 생활 환경을 개선하기 위해 군집으로 뭉친다는 것입니다. 식민지의 각 유기체는 평균적으로 포식자와의 싸움에서 살아남을 확률이 더 높으며 식민지는 개별 유기체에 비해 먹이를 더 효율적으로 검색하고 처리 및 저장할 수 있습니다. 즉 모든 유기체 군집은 존재하는 동안 포식자로부터의 손실을 최소화하면서 먹이의 양을 최대화하는 등 다양한 최적화 문제를 다양한 수준의 효율성으로 해결합니다. 이러한 생각들이 다양한 수학적 최적화 방법 구축의 기초를 형성했습니다.
파티클 스웜은 개발된 이후부터 가장 유명하고 인기 있는 최적화 알고리즘 중 하나입니다. 이 알고리즘을 다양하게 구현해 본 많은 저자들은 이 알고리즘이 인수가 많은 복잡한 함수를 최적화하는 데 매우 효과적이며 신경망 훈련에도 적합하다고 주장합니다.
이 기사에서는 알고리즘이 실제로 복잡한 문제를 해결하는 데 좋은지 알아 볼 것입니다. 고전적인 버전의 알고리즘과 수정된 많은 버전에서는 최적화 함수가 매끄럽고 연속적이어야 한다는 사실과 관련된 중요한 제한 사항이 있으므로 이산 함수에는 완전히 적합하지 않습니다. 그러나 일련의 기사에 따라 고려중인 모든 알고리즘은 적어도 알고리즘이 순전히 기술적으로 작동하도록 단점을 제거하기 위해(제한이 있다면) 변경될 것입니다. 즉 모든 알고리즘은 (트레이더 문제에서처럼) 함수의 평활성에 무관심해야 하며 전달인자 단계에 제한이 없어야 합니다.
2. 알고리즘 원리
이전 글에서는 최적화의 세계를 소개했지만 메인 프로그램(EA, 스크립트, 인디케이터)과 최적화 알고리즘 코어 간의 상호 작용 원리에 대해서는 다루지 않았습니다. 어떤 경우에도 세심한 독자는 알고리즘과 예제 프로그램이 왜 그런 식으로 작성되었는지 의문을 가질 것이기 때문에 주의를 기울이는 것이 중요합니다. 기존 버전의 최적화 알고리즘은 알고리즘이 주 실행 프로그램인 반면 외부 객체에 대한 적합도 함수는 알고리즘이 참조하는 방식으로 구성됩니다.
아래 그림 1은 알고리즘이 최적화된 파라미터를 적합도 함수에 전달하고 적합도 값(평가 기준)을 다시 가져오는 다이어그램을 보여줍니다. 이 시스템은 트레이더들은 물론 일반 사용자들이 문제를 해결하기 위한 프로그램을 구축하는 데 불편합니다. 왜 불편할까요? 예를 들어 과거에 실행된 테스터를 호출할 수 없습니다.
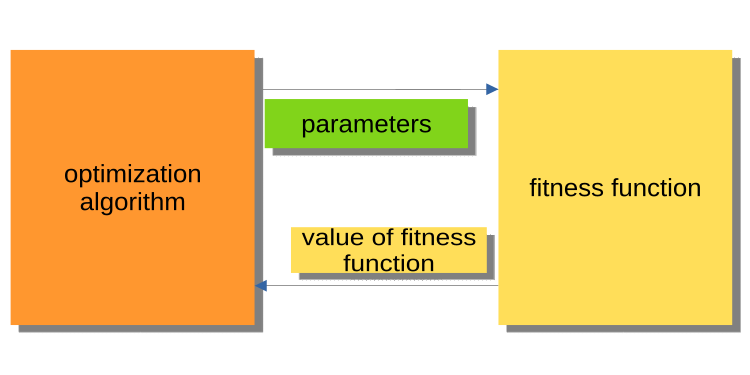
그림 1. PSO와 피트니스 함수 간의 상호 작용
그림 2에 표시된 구조가 훨씬 더 편리합니다. 여기서 최적화 알고리즘은 독립적인 프로그램이 아니라 별도의 모듈이거나 '블랙박스'입니다. 이 모듈에는 최적화된 각 전달 인자에 대해 '최소', '최대' 그리고 '단계'의 매개변수가 있습니다. MQL 프로그램은 요청 시 최적화된 전달 인자 받아 적합도 값, 즉 적합도 함수 값을 반환합니다. 이러한 구조를 통해 사용자 지정 최적화 관리자를 작성하기 위한 전문가 어드바이저의 자동 최적화 사용 등 유연한 솔루션을 다양하게 구축할 수 있습니다.
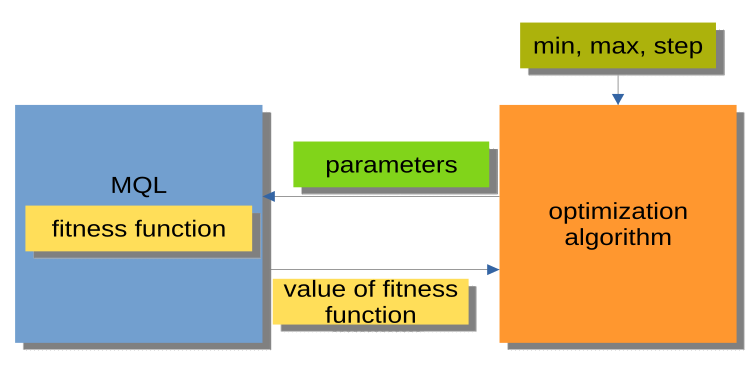
그림 2. MQL 프로그램과 PSO 간의 상호 작용
또한 최적화 알고리즘 메소드(그림 2의 MQL 블록)를 호출하는 구성은 모든 최적화 알고리즘(AO)에 대해 동일한 일반 체계로 나타낼 수 있다는 점도 알아 두시기 바랍니다.
Initialization_АО_0
반복 주기(에포크)
{
1) Method_АО_1
2) 최적화된 파라미터의 각 변형에 대한 적합도 값 얻기
3) Method_АО_2
}
따라서 세 가지 퍼블릭 메소드만 사용되는 것을 알 수 있습니다: Initialization_АО_0, Method_АО_1 and Method_АО_2. 이는 사용자 프로젝트가 복잡하더라도 최적화 프로세스를 구성하는 데 충분합니다.
PSO 워크플로 자체는 그림 3에 표시되어 있으며 다음과 같은 논리적 단계가 있습니다:
- 랜덤 파티클 생성(첫 번째 반복)
- 각 파티클에 대한 적합도 값 구하기
- 일반적인 모든 파티클에 대한 적합도 값 구하기
- 파티클 속도 조정
- 중단점 또는 2단계로 이동
- 프로그램 완료.

그림 3. PSO 동작 흐름
파티클 스웜 알고리즘을 좀 더 자세히 살펴보겠습니다.
스웜 인텔리전스 시스템은 서로 상호작용하고 환경과 상호작용하는 많은 파티클들로 구성됩니다. 각 파티클은 간단한 규칙을 따르지만 각 파티클이 무엇을 해야 하는지 알려주는 중앙 집중식의 행동 제어 시스템은 없습니다. 이들 간의 국지적이고 무작위적인 상호작용으로 인해 개인이 통제할 수 없는 지능적인 집단 행동이 출현하게 됩니다.
무리에 비유하자면 모든 파티클은 간단한 작업들을 수행해야 한다고 할 수 있습니다:
- 다른 파티클과 교차하지 않도록 합니다;
- 주변 파티클의 속도에 따라 속도를 조정합니다;
- 자신과 환경 사이의 거리를 상당히 좁게 유지하려고 하도록 해야 합니다.
PSO 알고리즘은 모집단 초기화와 함께 시작됩니다. 두 번째 단계는 각 파티클의 적합도 값을 계산한 후 개별 및 글로벌 최고 점수를 업데이트한 다음 파티클의 속도와 위치를 업데이트하는 것입니다. PSO를 사용할 때 수치 최적화 문제에 대한 해결책은 파티클의 위치로 표시됩니다. 또한 각 파티클은 절대 크기와 더 나은 새로운 솔루션/위치로 향하는 방향을 반영하는 현재의 속도를 가지고 있습니다.
또한 파티클은 적합도 값, 현재 위치, 가장 잘 알려진 위치(가장 잘 알려진 체력을 가진 이전 위치) 및 가장 잘 알려진 위치의 적합도 역시 저장합니다. 완료 조건이 충족될 때까지 2단계부터 4단계까지가 반복됩니다. 첫 번째 반복에서는 모든 파티클을 분산하여 최적의 솔루션을 찾습니다(탐색). 모든 파티클이 평가됩니다. 이웃 토폴로지에 대한 최적의 솔루션을 찾고 스웜의 각 구성원에 대한 개인 및 글로벌 최적 파티클을 업데이트합니다. 수렴은 모든 파티클을 최적의 솔루션을 가진 입자로 끌어당기는 방식으로 이루어집니다.
PSO 알고리즘은 핵심은 매우 간단하지만 이 글의 코드를 여러분의 필요에 맞게 수정하려면 알고리즘에 대한 이해가 필요합니다. PSO는 반복적인 프로세스입니다. 메인 처리 루프의 각각의 반복에서 각 파티클의 현재 속도가 먼저 업데이트됩니다. 파티클의 현재 속도, 로컬 정보, 스웜의 글로벌 정보가 고려됩니다. 그런 다음 각각의 파티클의 위치는 해당 파티클의 새로운 속도 값을 사용하여 업데이트됩니다.
수학적으로 이 두 파티클 좌표 업데이트 방정식은 다음과 같습니다:
V(T+1) = W * V(T) + C1 * RP * (P(T) - X(T)) + (c2 * rg * (g(t) - x(t))
X(T+1) = X(T) + V(T+1)
위치 업데이트 프로세스는 실제로 제안된 방정식보다 훨씬 간단합니다. 첫 번째 방정식은 파티클의 속도를 업데이트하는 방정식입니다.
용어 v(t+1)는 t+1 시점의 속도를 나타냅니다. 새로운 속도는 세 가지 조건에 따라 달라집니다.
- 첫 번째: w * v(t). w 계수는 weight fraction of inertia이라고 하며 상수이고, v(t)는 시간 t의 현재 속도입니다.
- 두 번째 : c1 * rp * (p(t) - x(t)). c1 계수는 cognitive (or personal, or local) weight fraction이라고 하는 상수입니다. rp 승수는 [0, 1] 범위의 무작위 변수입니다. p(t) 벡터의 양은 지금까지 발견된 파티클의 최적 위치이고, x(t) 벡터의 양은 파티클의 현재 위치입니다.
- 세 번째: 속도 업데이트 c2 * rg * (g(t) - x(t). c2 계수는 소셜(또는 글로벌) weight fraction이라고 하는 상수입니다. rg 승수는 [0, 1] 범위의 무작위 변수입니다. g(t) 벡터의 값은 스웜의 파티클 중 지금까지 발견된 가장 잘 알려진 위치입니다. 새로운 속도인 v(t+1)가 결정되면 파티클의 새로운 위치 x(t+1)를 계산하는 데 사용됩니다.
3. 고전적 구현
공간의 좌표 집합(최적화된 파라미터)을 설명하는 논리 단위는 파티클이며 파티클은 구조로 나타낼 수 있는데, 여기서 c[]는 파티클의 좌표, cB[]는 모든 반복에 대한 파티클의 최적 좌표로, v[]는 파티클의 각 좌표에 대한 속도로, ff - 파티클의 현재 적합성 값, ffB - 모든 반복에 대한 파티클의 최적 적합성 값으로 표현할 수 있습니다. 파티클 구조의 생성자에서는 알고리즘이 함수의 최대값을 찾도록 설계되었기 때문에 'double' 유형으로 표현할 수 있는 최소값을 사용하여 ff 및 ffB의 값을 초기화합니다(최소값을 찾으려면 결과 적합도 값 앞에 "-" 기호를 추가하면 됩니다).
//—————————————————————————————————————————————————————————————————————————————— struct S_Particles { public: double c []; //coordinates double cB []; //best coordinates double v []; //velocity double ff; //the value of the fitness function double ffB; //best value fitness function S_Particles () { ff = -DBL_MAX; ffB = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
PSO 알고리즘을 세 개의 공용 메서드 InitPS (), Preparation ( ), Dwelling ()(Initialization_АО_0, Method_АО_1, Method_АО_2)만 있는 클래스로 구현해 보겠습니다. 프라이빗 메서드 중 GenerateRNDparticles () 와 ParticleMovement ( )는 PSO에 고유하며 나머지는 이전 글에서 이미 알아보았습니다. p [] 구조체 배열은 파티클의 스웜입니다. 각 파티클에는 적합도 값, 자체 좌표, 최적 좌표가 있을 뿐만 아니라 스웜 전체에는 최적 좌표 cB와 최적 적합도 값 ffB가 있습니다.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_PSO { public: //---------------------------------------------------------------------------- S_Particles p []; //particles double rangeMax []; //maximum search range double rangeMin []; //manimum search range double rangeStep []; //step search double cB []; //best coordinates double ffB; //FF of the best coordinates void InitPS (const int params, //number of opt. parameters const int size, //swarm size const double inertiaP, //inertia const double selfBoostP, //boost const double groupBoostP); //group boost void Preparation (); void Dwelling (); private: //---------------------------------------------------------------------------- int swarmSize; //swarm size int parameters;//number of optimized parameters double inertia; double selfBoost; double groupBoost; bool dwelling; void GenerateRNDparticles (); void ParticleMovement (); double SeInDiSp (double in, double inMin, double inMax, double step); double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
InitPS () 메서드는 최적화가 시작되기 전에 알고리즘을 초기화하기 위한 것입니다(Initialization_АО_0). 메서드 인자 값은 메서드의 프라이빗 멤버에 할당되며 크기는 스웜과 스웜 내 각 파티클의 내부 파라미터에 할당됩니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::InitPS (const int paramsP, const int sizeP, const double inertiaP, const double selfBoostP, const double groupBoostP) { ffB = -DBL_MAX; parameters = paramsP; swarmSize = sizeP; ArrayResize (rangeMax, parameters); ArrayResize (rangeMin, parameters); ArrayResize (rangeStep, parameters); dwelling = false; inertia = inertiaP; selfBoost = selfBoostP; groupBoost = groupBoostP; ArrayResize (p, swarmSize); for (int i = 0; i < swarmSize; i++) { ArrayResize (p [i].c, parameters); ArrayResize (p [i].cB, parameters); ArrayResize (p [i].v, parameters); } ArrayResize (cB, parameters); } //——————————————————————————————————————————————————————————————————————————————
Preparation () 메서드는 각 반복(에포크)에서 먼저 호출됩니다(Method_АО_1). 이 메서드는 간단하지만 매우 중요합니다. 메서드가 첫 번째 에포크에서 호출될지 후속 에포크에서 호출될지(dwelling 플래그에 따라 결정됨)에 따라 스웜 적합도 값이 리셋되고 랜덤 스웜 집단이 생성되거나 파티클이 새로운 좌표로 이동합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::Preparation () { if (!dwelling) { ffB = -DBL_MAX; GenerateRNDparticles (); dwelling = true; } else ParticleMovement (); } //——————————————————————————————————————————————————————————————————————————————
무작위 스웜 집단은 GenerateRNDparticles () 메서드에서 생성됩니다. 파티클은 각각에 대해 지정된 범위의 임의의 좌표와 각 좌표에 대해 임의의 속도를 갖습니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::GenerateRNDparticles () { for (int s = 0; s < swarmSize; s++) { for (int k = 0; k < parameters; k++) { p [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); p [s].c [k] = SeInDiSp (p [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); p [s].cB [k] = p [s].c [k]; p [s].v [k] = RNDfromCI (0.0, (rangeMax [k] - rangeMin [k]) * 0.5); } } } //——————————————————————————————————————————————————————————————————————————————
ParticleMovement () 메서드는 파티클을 새로운 위치로 이동하는 알고리즘을 트리거합니다. 이를 위해서는 위의 방정식에 따라 각각의 좌표에 대한 속도를 계산해야 합니다. 위치는 기본적으로 변위 값으로 즉 입자가 현재 위치와 이동해야 하는 위치 사이의 차이인데 왜 "속도"라는 용어를 사용했는지 모르겠습니다. 각 좌표에 대해 이 차이를 계산한 후 현재 값에 더하기만 하면 됩니다. 그런 다음 주어진 스텝에서 최적화된 파라미터(파티클의 경우 좌표)의 최소/최대 경계를 초과하는 것이 허용되지 않는지 확인합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::ParticleMovement () { double rp; //random component of particle movement double rg; double velocity; double posit; double positBest; double groupBest; for (int i = 0; i < swarmSize; i++) { for (int k = 0; k < parameters; k++) { rp = RNDfromCI (0.0, 1.0); rg = RNDfromCI (0.0, 1.0); velocity = p [i].v [k]; posit = p [i].c [k]; positBest = p [i].cB [k]; groupBest = cB [k]; p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit); p [i].c [k] = posit + p [i].v [k]; p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } } } //——————————————————————————————————————————————————————————————————————————————
Dwelling () 메서드는 최적화에 사용되는 알고리즘의 세 번째 공개 메서드입니다(Method_АО_2). 이 메서드의 목적은 이전 성능과 비교하여 각 파티클의 최적 좌표와 적합성 값을 업데이트하고 필요한 경우 스웜의 적합성과 스웜의 최적 좌표를 업데이트하는 것입니다. 이 메서드는 반복 루프에서 적합성 값을 가져온 후 호출됩니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::Dwelling () { for (int i = 0; i < swarmSize; i++) { //remember the best position for the particle if (p [i].ff > p [i].ffB) { p [i].ffB = p [i].ff; for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k]; } if (p [i].ff > ffB) { ffB = p [i].ff; for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k]; } } } //——————————————————————————————————————————————————————————————————————————————
지정된 범위에서 주어진 단계를 가진 'double' 수를 discretization 하는 함수입니다.
//—————————————————————————————————————————————————————————————————————————————— // Choice in discrete space double C_AO_PSO::SeInDiSp (double in, double inMin, double inMax, double step) { if (in <= inMin) return (inMin); if (in >= inMax) return (inMax); if (step == 0.0) return (in); else return (inMin + step * (double)MathRound ((in - inMin) / step)); } //——————————————————————————————————————————————————————————————————————————————
이 함수는 지정된 범위에서 임의의 'double' 수를 가져오는 함수입니다.
//—————————————————————————————————————————————————————————————————————————————— // Random number generator in the custom interval double C_AO_PSO::RNDfromCI (double min, double max) { if (min == max) return (min); double Min, Max; if (min > max) { Min = max; Max = min; } else { Min = min; Max = max; } return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0))); } //——————————————————————————————————————————————————————————————————————————————
이론은 끝났습니다: 이제 연습에 들어가 보겠습니다.
그림 2에 설명 된 시리즈의 첫 번째 기사에서와 동일한 구조를 사용하여 알고리즘을 구성할 것이기 때문에 (앞으로도 계속이 작업을 수행 할 것입니다) 알고리즘을 테스트 스탠드에 연결하는 것이 어렵지 않을 것입니다.
스탠드를 실행하면 아래와 유사한 애니메이션이 표시됩니다. 이 경우 파티클 무리가 어떻게 작동하는지 명확하게 확인할 수 있습니다. 스웜은 실제로 스웜처럼 행동합니다. 함수의 히트 맵에서 함수는 짙은 구름의 형태로 움직입니다.
기억하시겠지만 검은색 원은 함수의 글로벌 최적(최대)을 나타내고, 검은색 점은 현재 반복 시점에서 얻은 검색 알고리즘의 최적 평균 좌표를 나타냅니다. 평균값의 출처를 설명해 드리겠습니다. 히트 맵은 좌표로 표시되는 2차원이며, 최적화 중인 함수에는 수백 개의 변수(측정값)가 포함될 수 있습니다. 따라서 결과는 좌표로 평균화 됩니다.
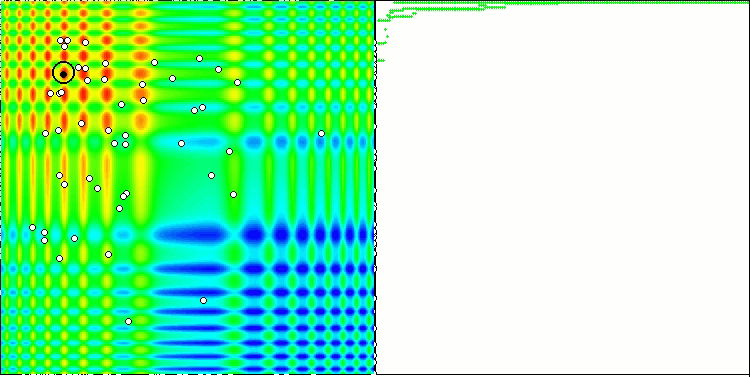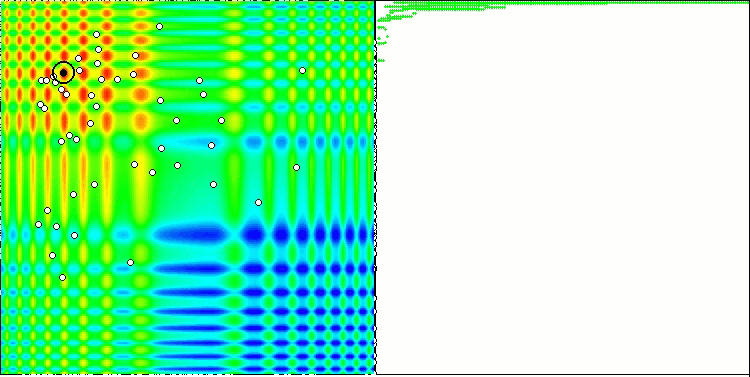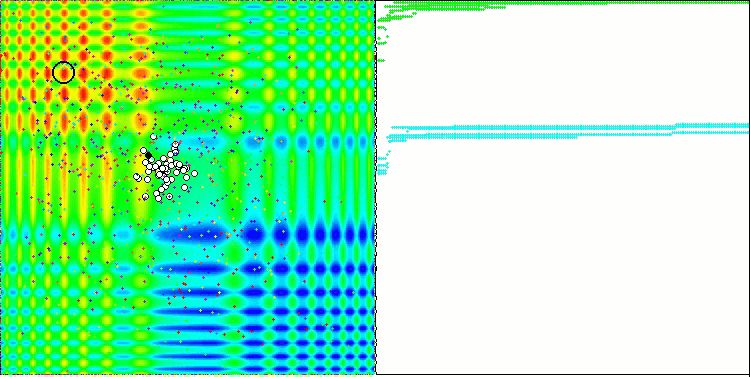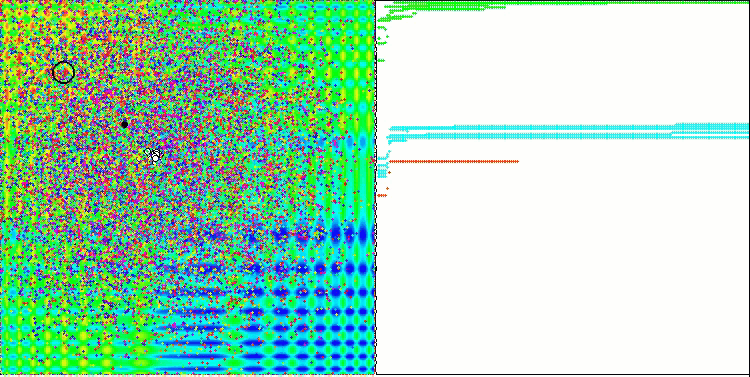
스킨 테스트 함수의 PSO.
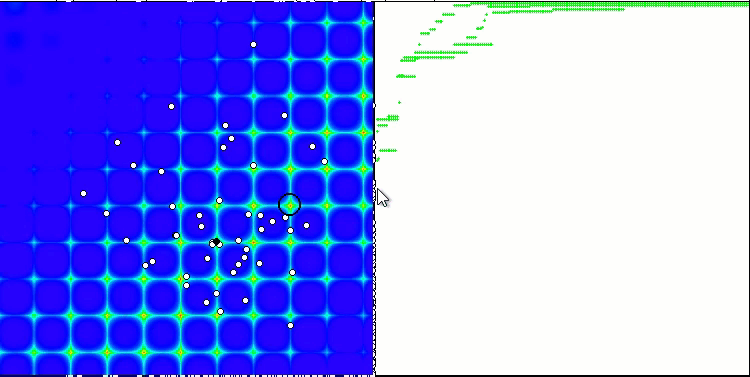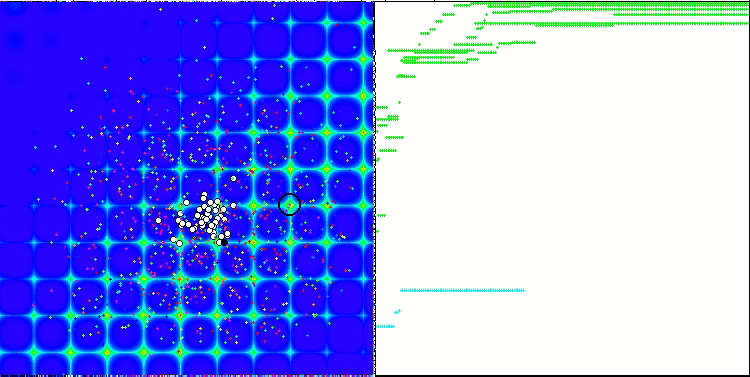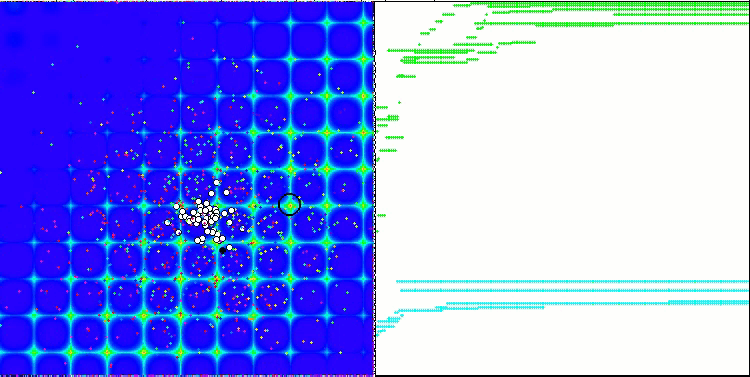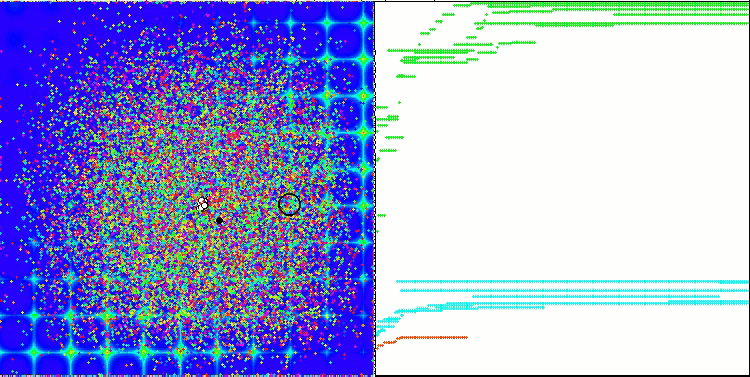
PSO의 포리스트 테스트 함수.
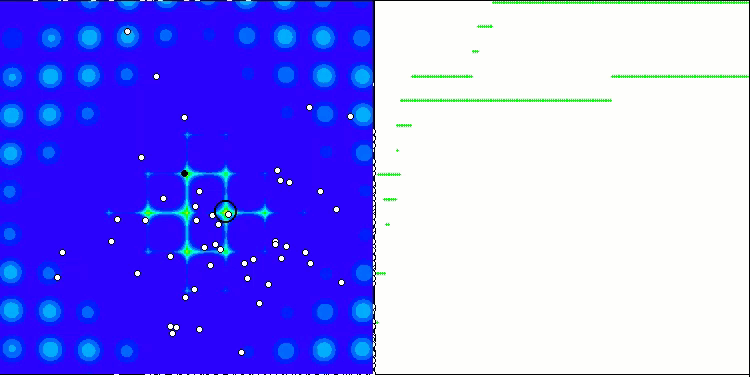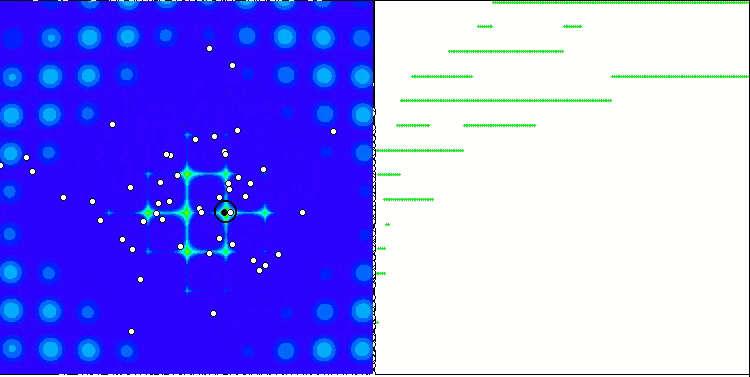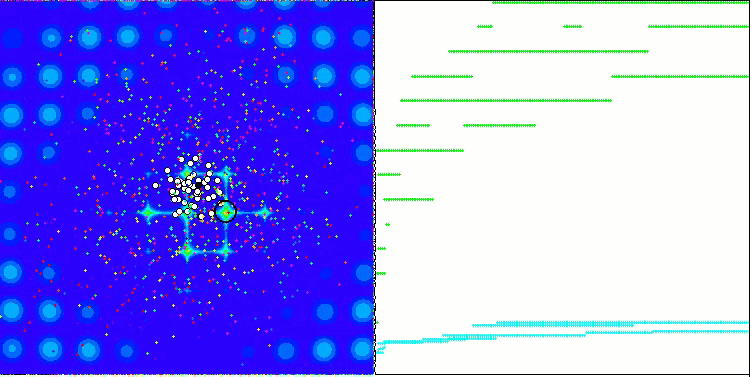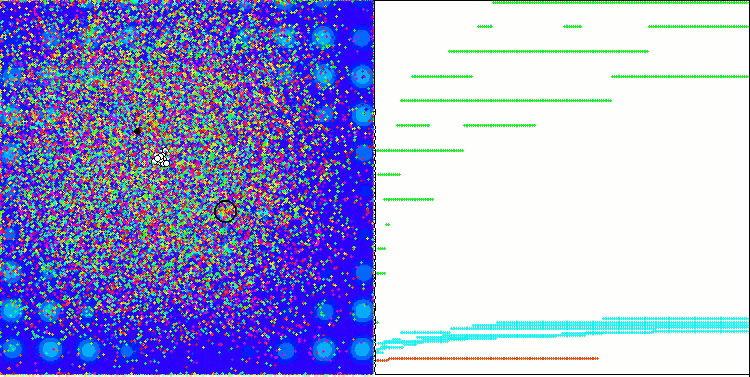
PSO의 메가시티 테스트 함수.
애니메이션에서 볼 수 있듯이 테스트 결과 PSO는 두 가지 변수를 최적화할 때만 부드러운 첫 번째 함수에 상당히 잘 대처하는 것으로 나타났습니다. 검색 공간의 크기가 증가하면 알고리즘의 효율성이 급격히 떨어집니다. 이는 특히 두 번째 및 개별적인 세 번째 함수에서 두드러집니다. 결과는 이전 글에서 설명한 무작위 알고리즘보다 눈에 띄게 나쁩니다. 이에 대해서는 결과 비교표를 작성할 때 자세히 논의할 것입니다.
유명한 PSO 알고리즘이 무작위 알고리즘에 부끄럽게 패배한 것을 보면 알고리즘에 다시 한 번 기회를 주고 싶을지도 모릅니다. 다음 섹션에서는 PSO 알고리즘을 수정해 보겠습니다.
4. 수정된 버전
제 생각에 PSO의 약점은 다음과 같습니다:
1) 각 좌표는 반드시 1과 거의 같은 확률로 변경됩니다. 즉 스웜의 각 파티클은 반복할 때마다 기껏해야 글로벌 영역의 국부적 극한 어딘가에서 진동하지만 최악의 경우 글로벌 극한 지점에 정확히 도달하지 못합니다. 이는 알고리즘의 특징인 국부적 극한에 갇히는 현상 즉 잘못된 수렴이 발생한다는 것을 의미합니다.
2) 알고리즘이 이산 함수에서 잘 작동하지 않는데 이는 부분적으로 첫 번째 결함 때문입니다. 파티클 좌표는 최적화되는 함수 표면의 가장 가까운 "영역"으로 이동하므로 국부 극단의 주변을 자세히 연구할 수 없습니다.
3) 새로운 영역을 탐색하는 것에 약한 알고리즘 능력. 떼는 국지적인 '홀'을 벗어나지 않고 한 곳에 집중합니다. 일부의 전문가들은 다중 군집 수정을 구현해보려는 시도를 하지만 관절 운동의 원칙뿐만 아니라 상호 반발의 가능성도 충족해야 하는 상호 거리의 원칙이 불분명하기 때문에 복잡한 다중 변수 함수를 최적화하는 문제는 여전히 풀리지 않은 상태입니다. 그렇지 않으면 개별 스웜이 단순히 한 영역이나 지점으로 모이기 때문에 이러한 구현은 의미가 없습니다. 이 와중에 간단한 1변수 또는 2변수 함수의 최적화는 뛰어난 수렴성을 가진 가장 간단한 방법으로 수행됩니다.
그렇다면 알고리즘을 개선하기 위해 무엇을 할 수 있을까요?
다른 파티클에서 얻어진 파티클에 최적의 개별 좌표를 전달해야 한다는 것은 분명한 사실입니다(반드시 그렇지는 않지만). "기증자" 입자의 전체 좌표가 좋을수록 좌표를 통과할 확률이 높아집니다. 입자 선택 확률의 변화는 그림 4에 개략적으로 나와 있습니다. 0에서 1 사이의 난수를 생성하고 포물선 함수로 결과 숫자를 변환한 다음 0에서 SwarmSize-1까지의 스웜 내 파티클의 일련 번호 범위에 맞게 스케일링합니다. 이를 위해서는 좌표 복사 확률인 PSOm(수정된 알고리즘)에 추가 파라미터를 도입해야 하며 파티클이 좋을수록 인덱스 0에 가까워지도록 스웜을 정렬해야 합니다.

그림 4. 시프트 파티클 선택 확률
ParticleMovement () 메서드를 약간 변경해 보겠습니다. 난수 [0;1]을 생성합니다. 숫자가 'copy' 매개변수보다 큰 것으로 판명되면 위에서 설명한 입자로 일반적인 작업을 수행하고 그렇지 않으면 그림 4에 표시된 규칙에 따라 선택한 인덱스로 다른 입자의 좌표를 복사합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSOm::ParticleMovement () { double rp; //random component of particle movement double rg; double velocity; double posit; double positBest; double groupBest; for (int i = 0; i < swarmSize; i++) { for (int k = 0; k < parameters; k++) { rp = RNDfromCI (0.0, 1.0); rg = RNDfromCI (0.0, 1.0); double rC = RNDfromCI (0.0, 1.0); if (rC > copy) { velocity = p [i].v [k]; posit = p [i].c [k]; positBest = p [i].cB [k]; groupBest = cB [k]; p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit); p [i].c [k] = posit + p [i].v [k]; p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } else p [i].c [k] = p [GetPartcileAdress ()].cB [k]; } } } //——————————————————————————————————————————————————————————————————————————————
Dwelling () 메서드도 변경해야 합니다. SortParticles () 정렬 함수 호출을 추가합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSOm::Dwelling () { for (int i = 0; i < swarmSize; i++) { //remember the best position for the particle if (p [i].ff > p [i].ffB) { p [i].ffB = p [i].ff; for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k]; } if (p [i].ff > ffB) { ffB = p [i].ff; for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k]; } } SortParticles (); } //——————————————————————————————————————————————————————————————————————————————
GetParticleAdress () 함수는 최적의 파티클을 향해 이동된 확률로 파티클의 주소를 선택할 수 있습니다.
//—————————————————————————————————————————————————————————————————————————————— //shift of probability in the smaller party (to an index 0) int C_AO_PSOm::GetParticleAdress () { double x = RNDfromCI (-1.0, 0.0); x = x * x; x = Scale (x, 0.0, 1.0, 0, swarmSize - 1); x = SeInDiSp (x, 0, swarmSize - 1, 1); return ((int)x); } //——————————————————————————————————————————————————————————————————————————————
SortParticles ( ) 함수는 기존의 버블 정렬입니다.
//—————————————————————————————————————————————————————————————————————————————— //Sorting of particles void C_AO_PSOm::SortParticles () { //---------------------------------------------------------------------------- int cnt = 1; int t0 = 0; double t1 = 0.0; //---------------------------------------------------------------------------- // We will put indexes in the temporary array for (int i = 0; i < swarmSize; i++) { ind [i] = i; val [i] = p [i].ffB; //ffPop [i]; } while (cnt > 0) { cnt = 0; for (int i = 0; i < swarmSize - 1; i++) { if (val [i] < val [i + 1]) { t0 = ind [i + 1]; t1 = val [i + 1]; ind [i + 1] = ind [i]; val [i + 1] = val [i]; ind [i] = t0; val [i] = t1; cnt++; } } } // On the received indexes create the sorted temporary population for (int u = 0; u < swarmSize; u++) pT [u] = p [ind [u]]; // Copy the sorted array back for (int u = 0; u < swarmSize; u++) p [u] = pT [u]; } //——————————————————————————————————————————————————————————————————————————————
한 숫자 범위에서 다른 숫자 범위로 숫자의 배율을 조정하는 함수입니다.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_PSOm::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return (OutMIN); if (In > InMAX) return (OutMAX); return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } } //——————————————————————————————————————————————————————————————————————————————
5. 테스트 결과
마지막으로 현재까지의 연구 결과를 요약해 보겠습니다. 안타깝게도 PSO 알고리즘은 아무리 좋은 결과를 바라고 싶어도 스스로를 정당화하지 못했습니다. 연구 결과 브레이크가 있고 인수가 많은 이산 함수의 경우 수렴이 약한 것으로 나타났습니다. 알고리즘을 수정하려는 시도는 실패했고 그 결과는 기존의 구현보다 훨씬 더 나쁜 것으로 나타났습니다.
복사 매개변수를 0.8에 가까운 값으로 늘리면 여전히 즉각적인 수렴을 보여줄 수 있지만 테스트에서 인수가 두 개 뿐인 경우에만 첫 번째 부드러운 함수에 대해서 가능합니다. 다른 테스트의 경우 이 매개변수는 결과를 악화시킬 뿐입니다. PSO의 고전적인 구현은 1000개의 인수가 있는 스킨 함수에서만 흥미로운 것을 보여줄 수 있었습니다. 다른 테스트는 평범한 것으로 판명되었습니다.
최종 테스트 결과는 기존 알고리즘의 경우 0.47695, 수정된 알고리즘의 경우 0.45144로 각각 나타났습니다. 결과는 아래 표에 나와 있습니다. 테스트 스탠드에서는 설정에서 테스트 실행 횟수를 선택할 수 있으므로(기본값은 5회) 컴퓨팅 성능이 허용하는 경우 이 매개변수를 더 높게 설정하면 통계적으로 더 정확한 결과를 얻을 수 있습니다.
| AO | 실행 | 피부 | 포리스트 | 메가시티(개별) | 최종 결과 | ||||||
| 2개 params(1 F) | 40개 params(20F) | 1000 params(500 F) | 2개 params(1 F) | 40개 params(20F) | 1000 params(500 F) | 2개 params(1 F) | 40개 params(20F) | 1000 params(500 F) | |||
| RND | 1000 | 0.98744 | 0.61852 | 0.49408 | 0.89582 | 0.19645 | 0.14042 | 0.77333 | 0.19000 | 0.14283 | 0.51254 |
| 10,000 | 0.99977 | 0.69448 | 0.50188 | 0.98181 | 0.24433 | 0.14042 | 0.88000 | 0.20133 | 0.14283 | ||
| PSO | 1000 | 0.98436 | 0.72243 | 0.65483 | 0.71122 | 0.15603 | 0.08727 | 0.53333 | 0.08000 | 0.04085 | 0.47695 |
| 10,000 | 0.99836 | 0.72329 | 0.65483 | 0.97615 | 0.19640 | 0.09219 | 0.82667 | 0.10600 | 0.04085 | ||
| PSOm | 1000 | 0.96678 | 0.64727 | 0.57654 | 0.80616 | 0.13388 | 0.06800 | 0.53333 | 0.08067 | 0.04211 | 0.45144 |
| 10,000 | 0.99505 | 0.64986 | 0.57654 | 0.90401 | 0.18194 | 0.07104 | 0.74667 | 0.10400 | 0.04211 | ||
위의 모든 내용을 요약하면 PSO는 정제된 검색 영역(로컬 검색 능력이 떨어지는)에서 느린 수렴을, 평균 최적점에서는 빠르고 조기 수렴을 유도하는 경향이 있습니다. 간단히 말해 이 알고리즘은 매우 약하며 복잡하고 훨씬 더 불 연속적인 함수, 특히 여러 인수가 있는 함수를 최적화하는 데 적합하지 않습니다.
일반적으로 PSO를 개선하는 데 사용할 수 있는 몇 가지 접근 방식이 있습니다. 스웜의 크기는 중요한 요소 중 하나입니다. 스웜 크기가 클수록 더 빠르고 정확하게 수렴할 가능성이 높아집니다. 그러나 실제 문제에서는 적합도 함수의 실행 횟수에 임계값이 있는 경우가 많으며 스웜의 크기를 늘리면 에포크 수가 비례적으로 줄어들어 스웜 진화의 가능성이 줄어듭니다.
두 번째 접근 방식은 탐험과 개척 사이의 균형을 맞추는 것입니다. 반복을 시작할 때 높은 수준의 개척을 통해 글로벌 최적에 가까운 솔루션을 찾을 확률이 높습니다. 한편 반복이 끝날 무렵에는 높은 수준의 개척을 통해 파티클이 유망한 영역에서 가장 정확한 솔루션을 찾을 수 있는 기회를 얻게 됩니다. 다른 방법으로는 스웜 단계 전에 사전 최적화를 수행하는 것도 PSO의 기본 성능을 개선하는 데 사용할 수 있는 또 다른 기법이며 오늘날에는 매우 일반적으로 사용됩니다. 각 하위 그룹에 서로 다른 작업이나 목표를 할당하면 다중 작업 문제에서 PSO의 효율성을 높일 수도 있습니다.
PSO의 성능을 개선하기 위한 또 다른 접근 방식은 속도 방정식의 구성 요소를 설정하는 것입니다(동적 속도 제어). 이러한 접근 방식은 파티클을 다른 방향으로 전송하여 글로벌 최적값에 더 빠르게 수렴하도록 할 수 있지만 이는 가정에 불과합니다.장점:
- 이 알고리즘은 매우 간단하고 컴퓨팅 리소스를 많이 차지하지 않으며 고전적인 구현에서는 배열을 정렬하지도 않기 때문에 코드가 매우 빠르게 작동합니다.
- 알고리즘은 원활한 함수들로 잘 작동합니다. 지금까지 PSO는 여러 인수가 있는 부드러운 함수를 최적화하는 데 있어 확실한 선두주자입니다.
단점:
- 최적화된 함수 학습의 품질이 낮습니다. 이 알고리즘은 여러 가지 고유한 솔루션 집합이 필요한 문제를 해결하는 데 적용할 수 없습니다.
- 낮은 속도와 컨버전스 정확도.
- 이산 함수 최적화에 적합하지 않습니다.
- 거의 완벽한 비확장성.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/11386
 Expert Advisor 개발 기초부터(18부): 새로운 주문 시스템(I)
Expert Advisor 개발 기초부터(18부): 새로운 주문 시스템(I)
 인구 최적화 알고리즘
인구 최적화 알고리즘
 Expert Advisor 개발 기초부터(19부): 새로운 주문 시스템(II)
Expert Advisor 개발 기초부터(19부): 새로운 주문 시스템(II)
 차이킨 오실레이터로 트레이딩 시스템을 설계하는 방법 알아보기
차이킨 오실레이터로 트레이딩 시스템을 설계하는 방법 알아보기