MetaTrader 5 / 예
English Русский 中文 Español Deutsch 日本語 Português Français Italiano Türkçe
preview
모집단 최적화 알고리즘: 회색 늑대 옵티마이저(GWO)

모집단 최적화 알고리즘: 회색 늑대 옵티마이저(GWO)

MetaTrader 5 — 예 | 29 8월 2023, 15:51
828 0
Andrey Dik
Andrey Dik

콘텐츠

1. 소개
2. 알고리즘에 대한 설명
3. 테스트 함수
4. 테스트 결과


1. 소개

회색 늑대 알고리즘은 2014년에 개발된 메타 휴리스틱 확률론적 군집 지능 알고리즘입니다. 이 아이디어는 회색 늑대 무리 사냥 모델을 기반으로 합니다. 늑대에는 알파, 베타, 델타, 오메가의 네 가지 유형이 있습니다. 알파는 의사 결정과 팩 관리에서 가장 많은 '비중'을 차지합니다. 다음은 알파에 복종하며 나머지 늑대들을 지배하는 베타 및 델타 늑대가 있습니다. 오메가 늑대는 항상 다른 지배적인 늑대에게 복종합니다.

늑대 계층 구조 수학적 모델에서 alpha-α-늑대는 무리의 지배적인 늑대이며 무리의 구성원들은 그의 명령을 수행해야 합니다. Beta-β-종속 늑대는 알파의 의사 결정을 보조하며 알파의 역할의 역할을 할 수 있는 가장 적합한 후보로 간주됩니다. Delta δ 늑대는 알파와 베타에 복종해야 하지만 오메가를 지배합니다. 오메가 ω 늑대는 무리의 희생양이자 가장 중요하지 않은 개체로 간주됩니다. 오메가는 먹이를 먹는 순서에서 마지막입니다. 알파가 가장 유리한 솔루션으로 간주됩니다.

두 번째와 세 번째로 좋은 솔루션은 각각 베타 및 델타입니다. 나머지 솔루션은 오메가로 간주됩니다. 나머지 늑대들이 가장 적합한 늑대(알파, 베타, 델타), 즉 먹잇감에 가장 가까운 늑대에게 접근한다고 가정합니다. 각각의 접근 후 이 단계에서 누가 알파, 베타, 델타인지 결정한 다음 늑대들을 다시 재배치합니다. 무리의 대형은 늑대가 무리에 모일 때까지 이루어지며 이는 최소한의 거리로 공격할 수 있는 최적의 방향이 됩니다.

알고리즘 동안 늑대가 먹이를 찾고 포위하고 공격하는 3 가지 주요 단계가 수행됩니다. 검색을 통해 먹잇감에 가장 가까운 늑대인 알파, 베타, 델타 늑대를 찾아냅니다. 나머지 개체들은 우세한 개체에게 순종하여 먹이를 둘러싸기 시작하거나 최선의 선택을 찾기 위해 무작위로 계속 움직일 수 있습니다.


2. 알고리즘에 대한 설명

무리의 계층 구조는 그림 1에 개략적으로 표시되어 있습니다.  알파가 지배적인 역할을 합니다.

지배력

그림 1. 늑대 무리의 사회적 위계질서




수학적 모델 및 알고리즘
소셜 계층 구조:

  • 알파 늑대(α) 형태의 최상의 솔루션입니다.
  • 베타 늑대(β)로서 두 번째로 좋은 솔루션입니다.
  • 델타 늑대(δ)로서 세 번째로 좋은 솔루션입니다.
  • 오메가 늑대(ω)와 같은 다른 가능한 솔루션.

먹이 포위하기: 이미 최고의 알파, 베타, 델타 솔루션이 있다면 추가적인 조치가 있을지의 여부는 오메가에 달려 있습니다.



스테이지

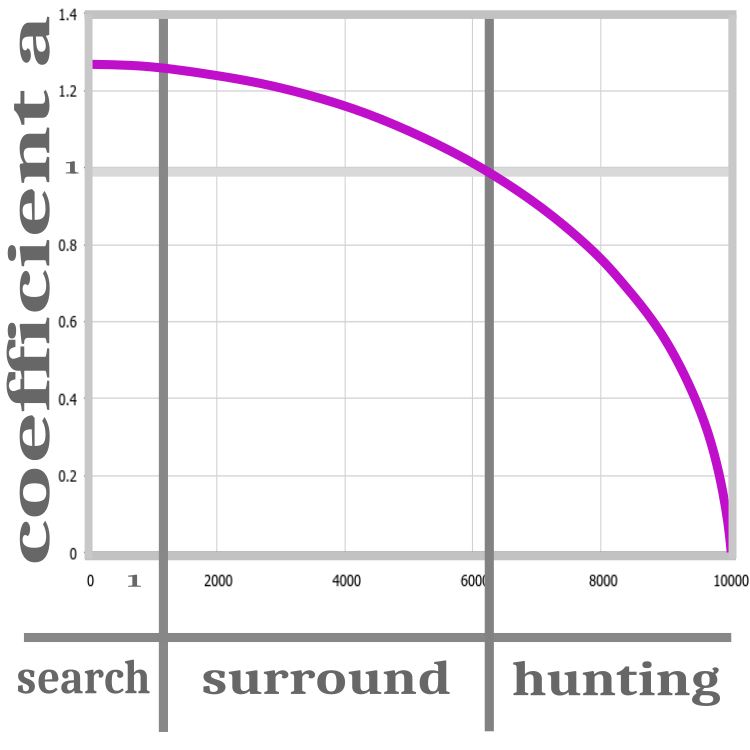
그림 2. 사냥 단계: 수색, 포위, 공격.


알고리즘의 모든 반복은 검색, 포위, 사냥의 세 단계로 표현됩니다. 표준 버전의 알고리즘은 알고리즘의 수렴을 개선하기 위해 а 계산 비율을 도입한 것이 특징입니다. 비율은 각 반복마다 0으로 감소합니다. 비율이 1을 초과하면 늑대들의 초기화가 진행 중입니다. 이 단계에서는 먹이의 위치를 완전히 알 수 없으므로 늑대를 무작위로 배포해야 합니다.

"검색" 단계가 끝나면 피트니스 기능의 값이 결정되고 그 후에야 "포위" 단계로 진행할 수 있습니다. 이 단계에서 a 비율은 1보다 큽니다. 즉 예상 먹잇감의 위치를 세분화할 수 있습니다. 알파, 베타, 델타가 이전의 위치에서 멀어지고 있기 때문입니다. а 비율이 1이 되면 '공격' 단계가 시작되고 반복이 끝나기 전에 비율이 0이 되는 경향이 있습니다. 이렇게 하면 늑대가 먹잇감에게 접근하여 최적의 위치를 이미 찾았다는 것을 암시합니다. 이 단계에서 늑대 중 한 마리가 더 나은 해결책을 찾으면 먹이의 위치와 늑대의 계층 구조가 업데이트 되지만 비율은 여전히 0이 되는 경향이 있습니다. a를 변경하는 과정은 비선형 함수로 표현됩니다. 단계는 그림 2에 개략적으로 나와 있습니다.

오메가 늑대의 행동은 모든 시대에 걸쳐 변하지 않으며 현재 지배적인 개체의 위치 간의 기하학적 중심을 따라 구성됩니다. 그림 3에서 알파, 베타, 델타는 계수에 의해 주어진 반경을 가진 임의의 방향으로 이전의 위치에서 벗어나고 오메가는 그 사이에서 중심으로 이동하지만 반경 내에서 어느 정도의 확률 내에서 이탈합니다. 반지름은 а 비율을 결정하며 우리가 기억하는 것처럼 반지름이 변하면 그에 비례하여 반지름이 감소합니다.




주변

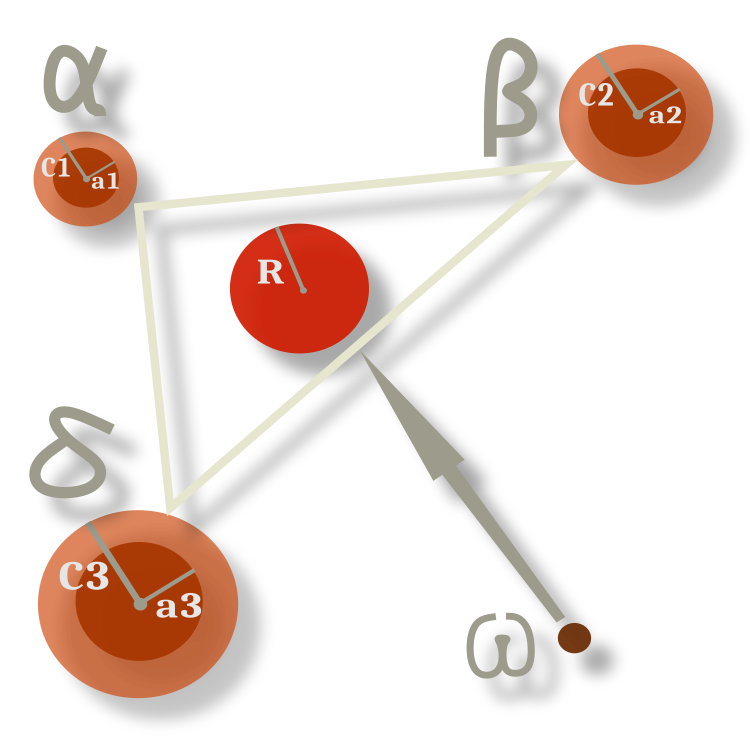
그림 3. 알파, 베타 및 델타와 관련된 오메가의 이동 다이어그램


GWO 알고리즘의 의사 코드는 다음과 같습니다:

1) 회색 늑대 개체 수를 무작위로 초기화합니다.
2) 인구의 각 구성원의 체력을 계산합니다.
3) 무리 리더:
-α = 최고의 피트니스 값을 가진 멤버
-β = 두 번째로 우수한 멤버(체력 기준)
-δ = 세 번째로 우수한 멤버(피트니스 값 기준)
α, β, δ에 따른 방정식에 따라 모든 오메가 늑대의 위치를 업데이트합니다.
4) 인구의 각 구성원의 체력을 계산합니다.
5) 3단계를 반복합니다.

알고리즘 코드로 넘어가 보겠습니다. 오리지널 버전에 추가한 유일한 것은 무리의 우두머리 늑대의 수를 설정할 수 있는 기능입니다. 이제 전체 무리에서 원하는 수의 리더를 설정할 수 있습니다. 이는 특정 작업에 유용할 수 있습니다.

우리는 평소와 같이 알고리즘의 기본 단위이자 문제의 해결책인 늑대부터 시작합니다. 이것은 좌표 배열과 먹이 값(적합도 함수)이 포함된 구조입니다. 리더와 하위 멤버의 구조는 동일합니다. 이렇게 하면 알고리즘이 단순화되고 우리는 루프 연산에서 동일한 구조를 사용할 수 있습니다. 또한 모든 반복 과정에서 늑대의 역할이 여러 번 변경됩니다. 역할은 정렬 후 배열의 위치에 따라 고유하게 결정됩니다. 리더는 배열의 시작 부분에 있습니다.

//——————————————————————————————————————————————————————————————————————————————
struct S_Wolf
{
  double c []; //coordinates
  double p;    //prey
};
//——————————————————————————————————————————————————————————————————————————————

늑대 무리는 작고 이해하기 쉬운 클래스로 표현됩니다. 여기에서 최적화할 매개변수의 범위와 단계, 최적의 생산 위치, 최적의 솔루션 값 및 보조 함수를 선언합니다.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GWO //wolfpack
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Wolf wolves    []; //wolves of the pack
  public: double cB        []; //best prey coordinates
  public: double pB;           //best prey

  public: void InitPack (const int    coordinatesP,   //number of opt. parameters
                         const int    wolvesNumberP,  //wolves number
                         const int    alphaNumberP,   //alpha beta delta number
                         const int    epochCountP);   //epochs number

  public: void TasksForWolves      (int epochNow);
  public: void RevisionAlphaStatus ();


  //============================================================================
  private: void   ReturnToRange (S_Wolf &wolf);
  private: void   SortingWolves ();
  private: double SeInDiSp      (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI     (double Min, double Max);

  private: int    coordinates;     //coordinates number
  private: int    wolvesNumber;    //the number of all wolves
  private: int    alphaNumber;     //Alpha beta delta number of all wolves
  private: int    epochCount;

  private: S_Wolf wolvesT    [];   //temporary, for sorting
  private: int    ind        [];   //array for indexes when sorting
  private: double val        [];   //array for sorting

  private: bool   searching;       //searching flag
};
//——————————————————————————————————————————————————————————————————————————————

일반적으로 클래스 선언 뒤에는 초기화가 이어집니다. 늑대의 체력의 최소 'double’ 값으로 재설정하고 배열의 크기를 분배합니다.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO::InitPack (const int    coordinatesP,   //number of opt. parameters
                         const int    wolvesNumberP,  //wolves number
                         const int    alphaNumberP,   //alpha beta delta number
                         const int    epochCountP)    //epochs number
{
  MathSrand (GetTickCount ());
  searching = false;
  pB        = -DBL_MAX;

  coordinates  = coordinatesP;
  wolvesNumber = wolvesNumberP;
  alphaNumber  = alphaNumberP;
  epochCount   = epochCountP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (ind, wolvesNumber);
  ArrayResize (val, wolvesNumber);

  ArrayResize (wolves,  wolvesNumber);
  ArrayResize (wolvesT, wolvesNumber);

  for (int i = 0; i < wolvesNumber; i++)
  {
    ArrayResize (wolves  [i].c, coordinates);
    ArrayResize (wolvesT [i].c, coordinates);
    wolves  [i].p = -DBL_MAX;
    wolvesT [i].p = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

각 반복에서 호출되는 첫 번째 퍼블릭 메서드는 가장 이해하기 어렵고 가장 방대한 양입니다. 알고리즘의 주요 로직은 다음과 같습니다. 실제로 알고리즘의 성능은 방정식으로 엄격하게 설명되는 확률적 메커니즘으로 제공됩니다. 이 방법을 단계별로 살펴봅시다. 첫 번째 반복에서 의도한 먹잇감의 위치를 알 수 없는 경우 플래그를 확인한 후 최적화된 매개변수의 최대값과 최소값을 생성하여 늑대를 임의의 방향으로 보냅니다.

//----------------------------------------------------------------------------
//space has not been explored yet, then send the wolf in a random direction
if (!searching)
{
  for (int w = 0; w < wolvesNumber; w++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      wolves [w].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      wolves [w].c [c] = SeInDiSp  (wolves [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
   
  searching = true;
  return;
}

알고리즘 설명의 표준 버전에는 벡터를 연산하는 방정식이 있습니다. 그러나 코드의 형태에서는 훨씬 더 명확합니다. 오메가 늑대 이동의 계산은 이전의 리더 값을 사용해야 하므로 알파, 베타, 델타 늑대 계산에 앞서 수행됩니다.

사냥의 세 단계(수색, 포위, 공격)를 제공하는 주요 구성 요소는 a 비율입니다. 이 비율은 현재 반복과 총 반복 횟수에 대한 비선형 의존성을 나타내며 0에 가까워지는 경향이 있습니다.
방정식의 다음 구성 요소는 Ai와 Сi입니다:
  • Ai = 2.0 * a * r1 - a;
  • Ci = 2.0 * r2;
여기서 r1과 r2는 [0.0;1.0] 범위의 난수입니다.
표현식에서
Xn += wolves [abd].c [c] - Ai * (Ci * wolves [abd].c [c] - wolves [w].c [c]);
늑대의 좌표는 리더 늑대의 평균값에 따라 조정됩니다. 알고리즘에서 원하는 수의 리더를 지정할 수 있으므로 좌표의 합산은 반복적으로 수행됩니다. 그 후 결과를 리더의 수로 나눕니다. 각 좌표에 대해 이 작업을 개별적으로 수행하여 매번 새로운 r1 및 r2 값을 생성합니다. 보시다시피 오메가 늑대의 새로운 위치는 리더의 현재 위치를 고려한 리더의 위치에 따라 조정됩니다.
//----------------------------------------------------------------------------
double a  = sqrt (2.0 * (1.0 - (epochNow / epochCount)));
double r1 = 0.0;
double r2 = 0.0;

double Ai = 0.0;
double Ci = 0.0;
double Xn = 0.0;

double min = 0.0;
double max = 1.0;

//omega-----------------------------------------------------------------------
for (int w = alphaNumber; w < wolvesNumber; w++)
{
  Xn = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    for (int abd = 0; abd < alphaNumber; abd++)
    {
      r1 = RNDfromCI (min, max);
      r2 = RNDfromCI (min, max);
      Ai = 2.0 * a * r1 - a;
      Ci = 2.0 * r2;
      Xn += wolves [abd].c [c] - Ai * (Ci * wolves [abd].c [c] - wolves [w].c [c]);
    }

    wolves [w].c [c] = Xn /= (double)alphaNumber;
  }

  ReturnToRange (wolves [w]);
}

리더들의 계산은 다음과 같습니다. 각 좌표에 대한 a, Ai 및 Ci 비율이 계산됩니다. 유일한 차이점은 리더의 위치가 현재의 가장 좋은 먹이 좌표와 자신의 위치에 따라 변경된다는 것입니다. 우두머리는 먹이 주위를 돌며 안팎으로 움직이면서 공격하는 하위 늑대들을 통제합니다.

//alpha, beta, delta----------------------------------------------------------
for (int w = 0; w < alphaNumber; w++)
{
  for (int c = 0; c < coordinates; c++)
  {
    r1 = RNDfromCI (min, max);
    r2 = RNDfromCI (min, max);

    Ai = 2.0 * a * r1 - a;
    Ci = 2.0 * r2;

    wolves [w].c [c] = cB [c] - Ai * (Ci * cB [c] - wolves [w].c [c]);
  }

  ReturnToRange (wolves [w]);
}

이것은 각 반복에서 호출되는 두 번째 퍼블릭 메서드입니다. 무리 내 리더의 상태는 여기에서 업데이트됩니다. 실제로 늑대는 체력 값에 따라 정렬됩니다. 군집 전체에 저장된 것보다 더 나은 먹이 좌표가 발견되면 우리는 값을 업데이트 합니다. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO::RevisionAlphaStatus ()
{
  SortingWolves ();

  if (wolves [0].p > pB)
  {
    pB = wolves [0].p;
    ArrayCopy (cB, wolves [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. 테스트 함수

스킨, 포레스트, 메가시티 함수들은 이미 알고 계실 겁니다. 이러한 테스트 함수들은 최적화 알고리즘을 테스트하기 위한 모든 복잡성 기준을 충족합니다. 그러나 한 가지 고려되지 않은 기능이 있습니다. 테스트의 객관성을 높이기 위해 구현해야 할 것이 있습니다. 요구 사항들은 다음과 같습니다:

  1. 글로벌 극값이 범위의 경계에 있어서는 안 됩니다. 알고리즘의 범위를 벗어난 검사가 없는 경우 알고리즘이 우수한 결과를 보여줄 수 있습니다. 이는 내부 결함으로 인해 값이 테두리에 위치하기 때문입니다.
  2. 글로벌 극값은 범위 좌표의 중앙에 있지 않아야 합니다. 이 경우 범위의 평균값을 생성하는 알고리즘이 고려됩니다.
  3. 글로벌 최소값은 좌표의 중앙에 위치해야 합니다. 이는 2페이지에 설명된 상황을 의도적으로 배제하기 위해 필요합니다.
  4. 테스트 함수의 결과를 계산할 때는 함수의 전체 영역에 걸쳐 무작위로 생성된 숫자(함수가 다변수인 경우)가 최대값의 약 50%의 평균 결과를 제공하는 경우를 고려해야 합니다. 그러나 실제로는 이러한 결과가 우연히 얻어지는 경우가 있습니다.

이러한 요구 사항을 고려하여 테스트 함수의 경계를 수정하고 범위의 중심을 함수 값들의 최소값으로 이동했습니다. 다시 한 번 요약해 드리겠습니다. 테스트 최적화 알고리즘 결과의 타당성과 객관성을 최대한 확보하기 위해 이 작업을 수행한 것입니다. 따라서 새로운 테스트 함수들에서 난수 생성에 기반한 최적화 알고리즘이 자연스럽게 낮은 결과를 보였습니다. 업데이트된 등급 표는 이 글의 마지막에 있습니다.

피부 함수. 여러 개의 로컬 극한값이 있는 평활화 함수는 최적화 알고리즘을 혼란스럽게 할 수 있으며 그 중 하나에 갇힐 수 있습니다. 유일한 글로벌 극값은 주변에서 값이 약하게 변화하는 것이 특징입니다. 이 함수는 알고리즘이 하나의 영역에 집중하지 않고 연구 중인 영역으로 나뉠 수 있다는 사실을 명확하게 보여줍니다. 특히 벌집(ABC) 알고리즘은 이러한 방식으로 작동합니다.

피부

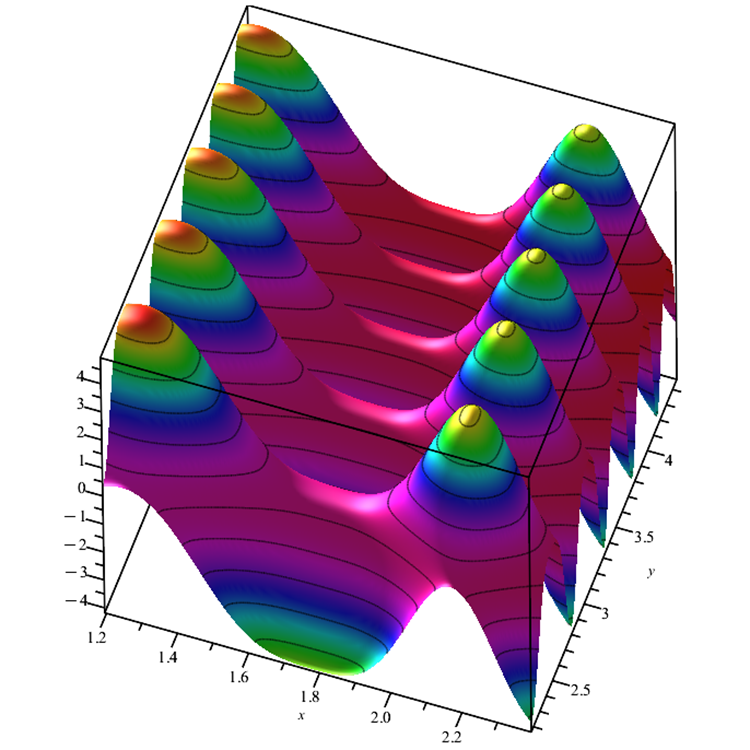
그림 4. 피부 테스트 함수

포리스트 함수. 여러 개의 평활화 극한과 여러 개의 미분할 수 없는 극한을 가진 함수입니다. 이는 '모래에서 바늘 찾기'를 위한 최적화 알고리즘의 가치 있는 테스트입니다. 하나의 전역 최대값을 찾는 것은 매우 어려운 작업이며 특히 함수에 많은 변수가 포함되어 있는 경우 더욱 그렇습니다. 개미 군집 알고리즘(ACO)은 이 작업에서 놀라운 방식으로 목표에 이르도록 하는 특출 난 행동으로 차별화되었습니다.



숲

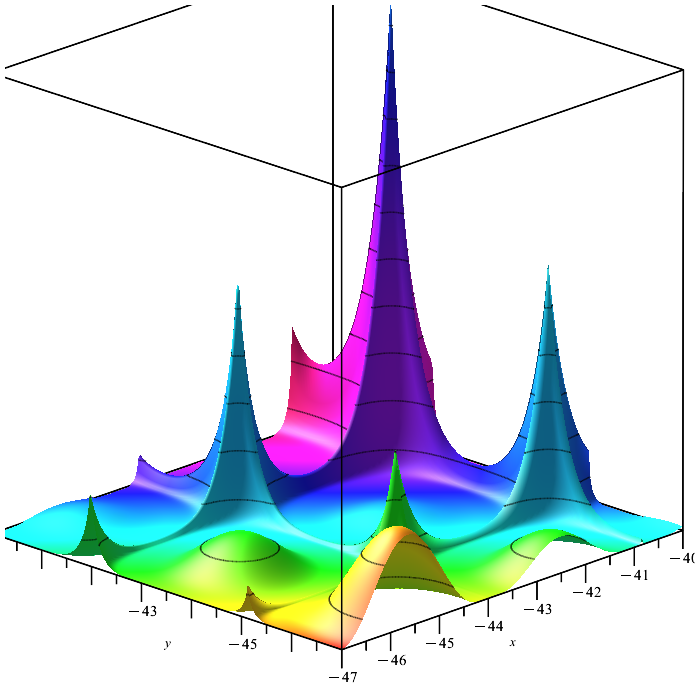
그림 5 포리스트 테스트 기능

메가시티 함수. 이 함수는 하나의 전역 극한과 여러 개의 로컬 극한이 있는 이산 최적화 문제입니다. 연구할 표면이 매우 복잡하면 그라데이션이 필요한 알고리즘을 테스트하기에 좋습니다. 글로벌 최대값에 대한 가능한 방향에 대한 정보를 제공하지 않는 최소값인 완전히 균일 한 "바닥"으로 인해 복잡성이 추가됩니다.


메가시티

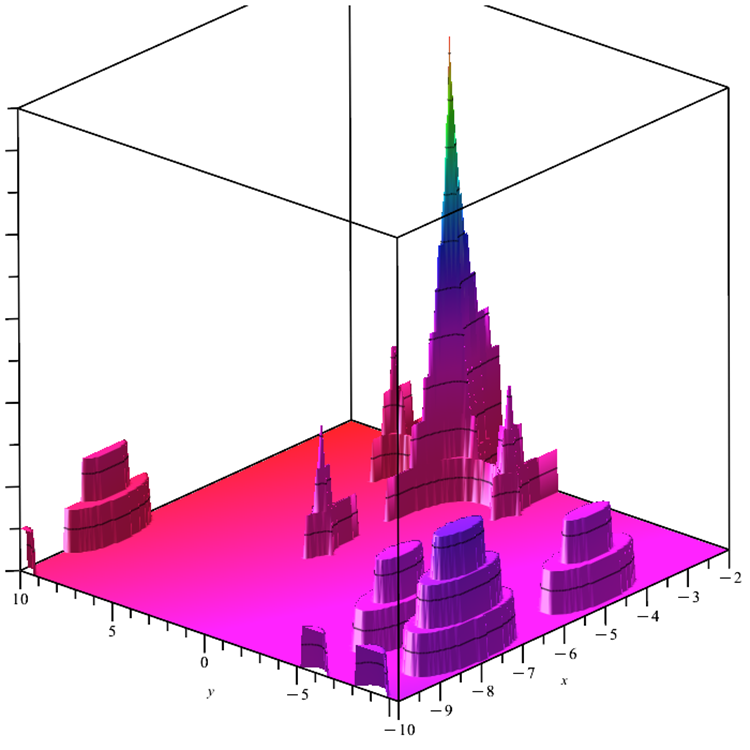
그림 6 메가시티 테스트 함수

범위를 벗어난 값에 대한 입력 인수를 검사하는 기능이 테스트 함수 코드에 추가되었습니다. 이전 버전의 함수에서는 최적화 알고리즘이 함수의 정의 범위 내에서 실제 함수보다 큰 함수 값을 얻게 되는 경우가 있었습니다.


4. 테스트 결과

테스트 함수들에 적용된 변경 사항으로 인해 테스트 스탠드도 업데이트되었습니다. 스탠드 화면의 오른쪽에서 최적화 알고리즘의 수렴 그래프를 계속 볼 수 있습니다. 녹색 선은 두 개의 변수가 있는 함수에 대한 컨버전스 결과를 나타냅니다. 파란색 선은 40개의 변수가 있는 함수를 나타냅니다. 빨간색은 1000개의 변수가 있는 함수를 의미합니다. 더 큰 검은색 원은 함수의 전역 최대값의 위치를 나타냅니다. 작은 검은색 원은 현재 최적화 알고리즘 솔루션 값의 위치를 나타냅니다. 흰색 선의 십자선은 테스트 함수의 기하학적 중심을 나타내며 글로벌 최소값에 해당합니다. 이는 테스트된 알고리즘의 동작을 더 잘 시각적으로 파악하기 위해 도입되었습니다. 흰색 점은 평균화 된 중간 솔루션을 나타냅니다. 색이 있는 작은 점은 해당 차원의 좌표의 쌍을 나타냅니다. 색상은 테스트 함수의 차원의 서수 위치를 나타냅니다.

이전 글에서 설명한 새로운 스탠드에서 최적화 알고리즘 테스트의 업데이트된 결과는 업데이트된 표에서 확인할 수 있습니다. 시각적 명확성을 높이기 위해 수렴 속도에 대한 선이 표에서 제거되었으며 선은 스탠드의 애니메이션에서 시각적으로 확인할 수 있습니다. 알고리즘 설명이 포함된 열을 추가했습니다.

ACOm(개미 군집 최적화) 테스트 결과:

2022.11.28 12:17:00.468 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:17:06.382 Test_AO_ACO (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.844203223078298
2022.11.28 12:17:06.382 Test_AO_ACO (EURUSD,M1) 점수: 0.98229
2022.11.28 12:17:14.191 Test_AO_ACO (EURUSD,M1) 20 Skin's; Func 10000 실행 결과: 4.043383610736287
2022.11.28 12:17:14.191 Test_AO_ACO (EURUSD,M1) 점수: 0.79108
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 1.2580170651681026
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) 점수: 0.12602
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:18:01.491 Test_AO_ACO (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.7678766100234538
2022.11.28 12:18:01.491 Test_AO_ACO (EURUSD,M1) 점수: 1.00000
2022.11.28 12:18:09.508 Test_AO_ACO (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 1.0974381500585855
2022.11.28 12:18:09.508 Test_AO_ACO (EURUSD,M1) 점수: 0.62077
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.20367726028454042
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) 점수: 0.11521
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:18:59.303 Test_AO_ACO (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 4.6
2022.11.28 12:18:59:303 Test_AO_ACO (EURUSD,M1) 점수: 0.38333
2022.11.28 12:19:07.598 Test_AO_ACO (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 5.28
2022.11.28 12:19:07.598 Test_AO_ACO (EURUSD,M1) 점수: 0.44000
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.2852
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) 점수: 0.02377
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) C_AO_ACOm에 대한 모든 점수: 0.4980520084646583

(인공 꿀벌 서식지) 테스트 결과:

2022.11.28 12:35:47.181 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:35:52.581 Test_AO_ABCm (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.918379986612587
2022.11.28 12:35:52.581 Test_AO_ABCm (EURUSD,M1) 점수: 1.00000
2022.11.28 12:35:59.454 Test_AO_ABCm (EURUSD,M1) 20 Skin's; Func 실행 10000 결과: 3.4073825805846374
2022.11.28 12:35:59.454 Test_AO_ABCm (EURUSD,M1) 점수: 0.63922
2022.11.28 12:36:32.428 Test_AO_ABCm (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 1.0684464927353337
2022.11.28 12:36:32.428 Test_AO_ABCm (EURUSD,M1) 점수: 0.08076
2022.11.28 12:36:32.428 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:36:38.086 Test_AO_ABCm (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.766245456669898
2022.11.28 12:36:38.086 Test_AO_ABCm (EURUSD,M1) 점수: 0.99908
2022.11.28 12:36:45.326 Test_AO_ABCm (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 0.35556125136004335
2022.11.28 12:36:45.326 Test_AO_ABCm (EURUSD,M1) 점수: 0.20112
2022.11.28 12:37:22.301 Test_AO_ABCm (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.06691711149962026
2022.11.28 12:37:22.301 Test_AO_ABCm (EURUSD,M1) 점수: 0.03785
2022.11.28 12:37:22.301 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:37:28.047 Test_AO_ABCm (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 12.0
2022.11.28 12:37:28.047 Test_AO_ABCm (EURUSD,M1) 점수: 1.00000
2022.11.28 12:37:35.689 Test_AO_ABCm (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 1.9600000000000002
2022.11.28 12:37:35.689 Test_AO_ABCm (EURUSD,M1) 점수: 0.16333
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.33880000000000005
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) 점수: 0.02823
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) C_AO_ABCm에 대한 모든 점수: 0.4610669021761763

ABC(인공 꿀벌 군집) 테스트 결과:

2022.11.28 12:29:51.177 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:29:56.785 Test_AO_ABC (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.890679983950205
2022.11.28 12:29:56.785 Test_AO_ABC (EURUSD,M1) 점수: 0.99339
2022.11.28 12:30:03.880 Test_AO_ABC (EURUSD,M1) 20 Skin's; Func 10000 실행 결과: 3.8035430744604133
2022.11.28 12:30:03.880 Test_AO_ABC (EURUSD,M1) 점수: 0.73381
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 1.195840100227333
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) 점수: 0.11118
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:30:42.811 Test_AO_ABC (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.7667070507449298
2022.11.28 12:30:42.811 Test_AO_ABC (EURUSD,M1) 점수: 0.99934
2022.11.28 12:30:50.108 Test_AO_ABC (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 0.3789854806095275
2022.11.28 12:30:50.108 Test_AO_ABC (EURUSD,M1) 점수: 0.21437
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.07451308481273813
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) 점수: 0.04215
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:31:31.510 Test_AO_ABC (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 10.2
2022.11.28 12:31:31.510 Test_AO_ABC (EURUSD,M1) 점수: 0.85000
2022.11.28 12:31:38.855 Test_AO_ABC (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 2.02
2022.11.28 12:31:38.855 Test_AO_ABC (EURUSD,M1) 점수: 0.16833
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.37559999999999993
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) 점수: 0.03130
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) C_AO_ABC의 모든 점수: 0.46043003186219245

PSO(파티클 스웜 최적화) 테스트 결과

2022.11.28 12:01:03.967 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:01:09.723 Test_AO_PSO (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.90276049713715
2022.11.28 12:01:09.723 Test_AO_PSO (EURUSD,M1) 점수: 0.99627
2022.11.28 12:01:17.064 Test_AO_PSO (EURUSD,M1) 20 Skin's; Func 10000 실행 결과: 2.3250668562024566
2022.11.28 12:01:17.064 Test_AO_PSO (EURUSD,M1) 점수: 0.38080
2022.11.28 12:01:52.880 Test_AO_PSO (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 0.943331687769892
2022.11.28 12:01:52.881 Test_AO_PSO (EURUSD,M1) 점수: 0.05089
2022.11.28 12:01:52.881 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:01:58:492 Test_AO_PSO (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.6577769478566602
2022.11.28 12:01:58:492 Test_AO_PSO (EURUSD,M1) 점수: 0.93772
2022.11.28 12:02:06.105 Test_AO_PSO (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 0.25704414127018393
2022.11.28 12:02:06.105 Test_AO_PSO (EURUSD,M1) 점수: 0.14540
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.08584805450831333
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) 점수: 0.04856
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:02:50.268 Test_AO_PSO (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 12.0
2022.11.28 12:02:50.268 Test_AO_PSO (EURUSD,M1) 점수: 1.00000
2022.11.28 12:02:57.649 Test_AO_PSO (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 1.1199999999999999
2022.11.28 12:02:57.649 Test_AO_PSO (EURUSD,M1) 점수: 0.09333
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.268
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) 점수: 0.02233
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) C_AO_PSO의 모든 점수: 0.40836715689743186

RND(무작위) 테스트 결과:

2022.11.28 16:45:15.976 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:45:21.569 Test_AO_RND (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.915522750114194
2022.11.28 16:45:21.569 Test_AO_RND (EURUSD,M1) 점수: 0.99932
2022.11.28 16:45:28.607 Test_AO_RND (EURUSD,M1) 20 Skin's; Func 10000 실행 결과: 2.584546688199847
2022.11.28 16:45:28.607 Test_AO_RND (EURUSD,M1) 점수: 0.44276
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 1.0161336237263792
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) 점수: 0.06827
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:46:09.622 Test_AO_RND (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.4695680943894533
2022.11.28 16:46:09.622 Test_AO_RND (EURUSD,M1) 점수: 0.83126
2022.11.28 16:46:17.675 Test_AO_RND (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 0.20373533112604475
2022.11.28 16:46:17.675 Test_AO_RND (EURUSD,M1) 점수: 0.11524
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.0538909816827325
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) 점수: 0.03048
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:47:00.219 Test_AO_RND (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 10.0
2022.11.28 16:47:00.219 Test_AO_RND (EURUSD,M1) 점수: 0.83333
2022.11.28 16:47:08.145 Test_AO_RND (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 1.08
2022.11.28 16:47:08.145 Test_AO_RND (EURUSD,M1) 점수: 0.09000
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.28840000000000005
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) 점수: 0.02403
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) C_AO_RND의 모든 점수: 0.38163317904126015



피부

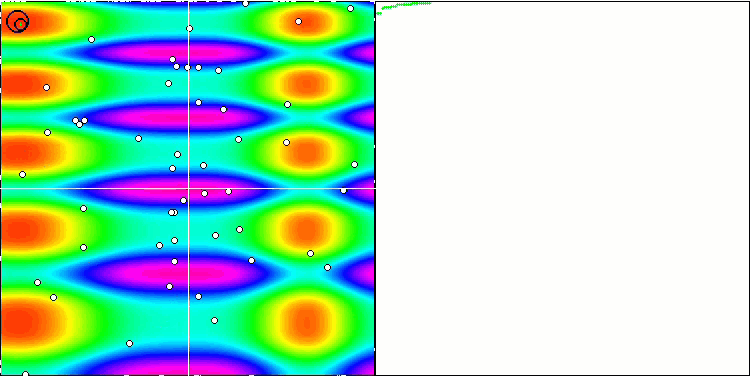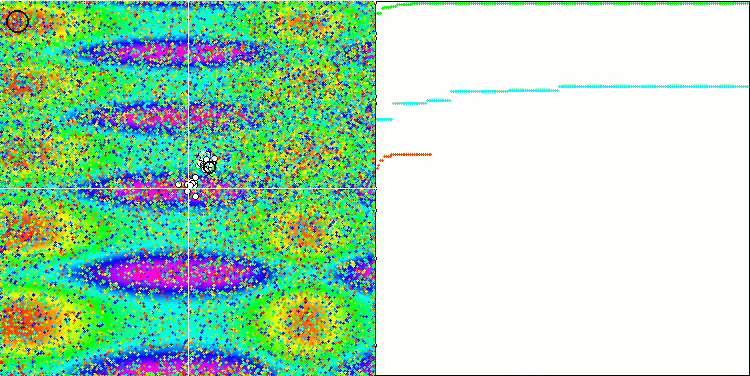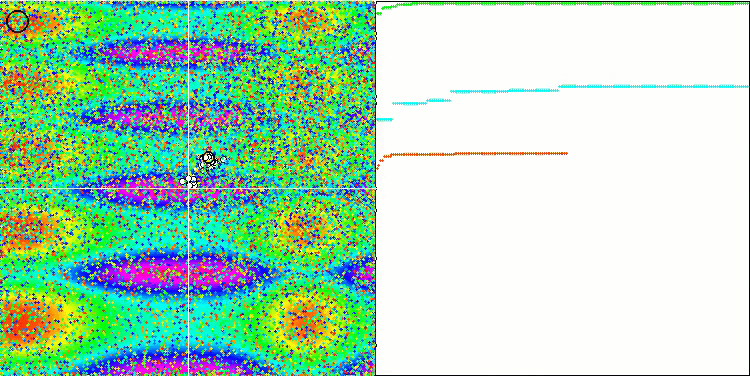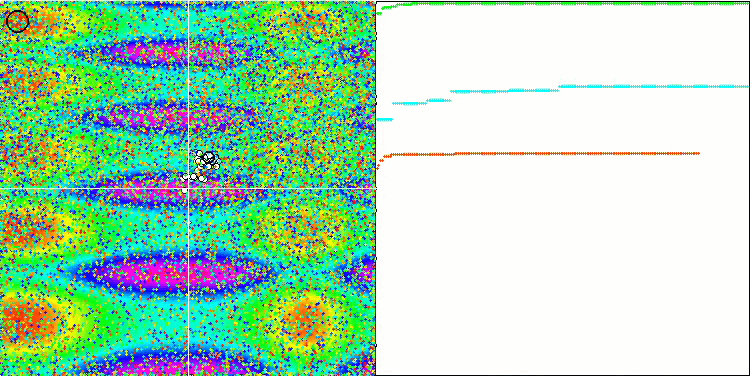
  피부 테스트 함수의 GWO

숲

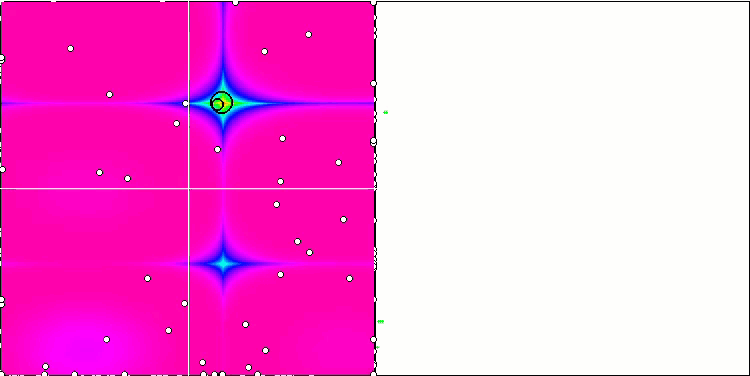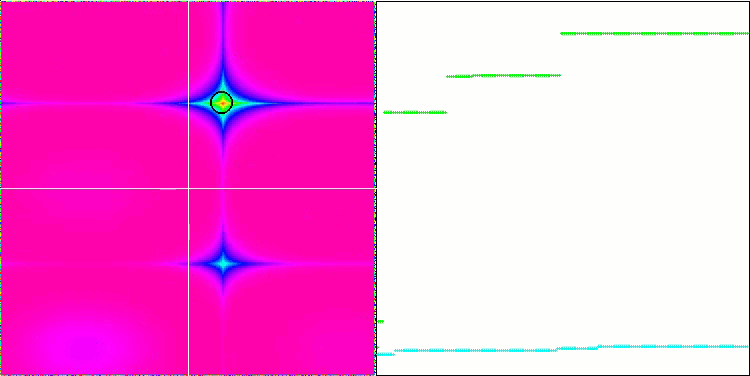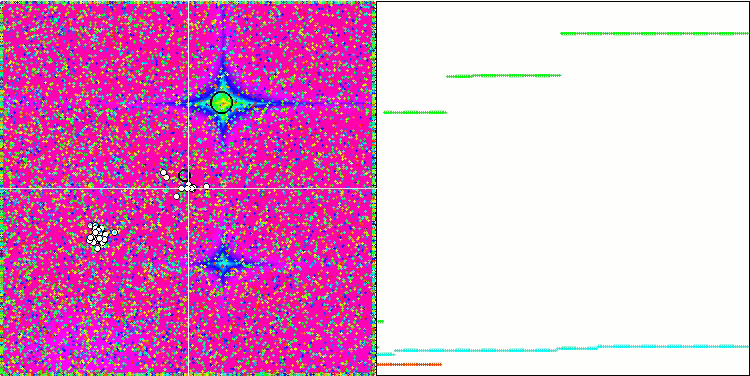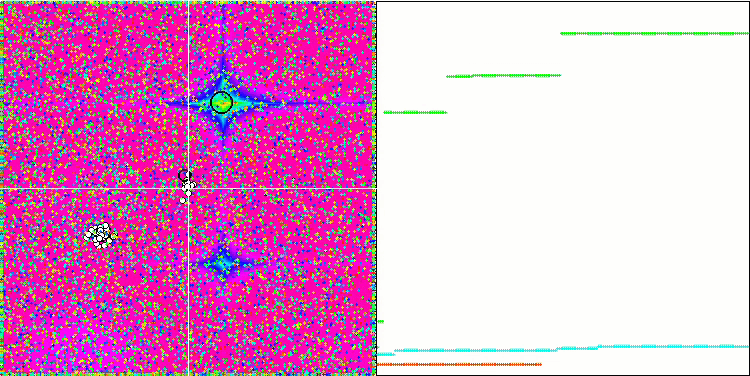
포레스트 테스트 함수의 GWO

메가시티

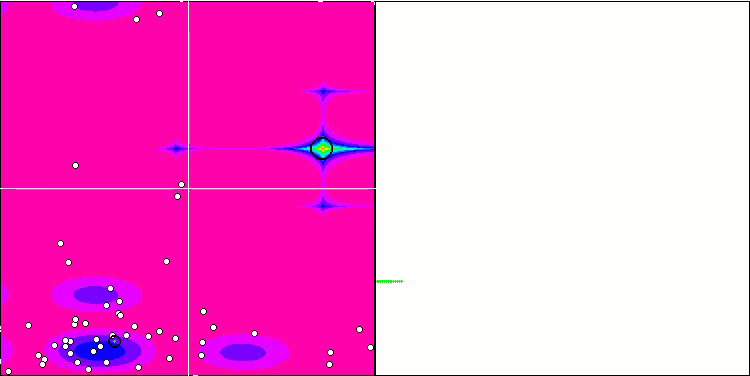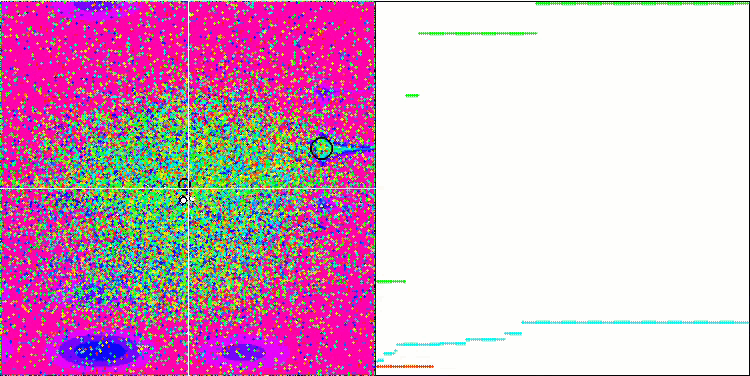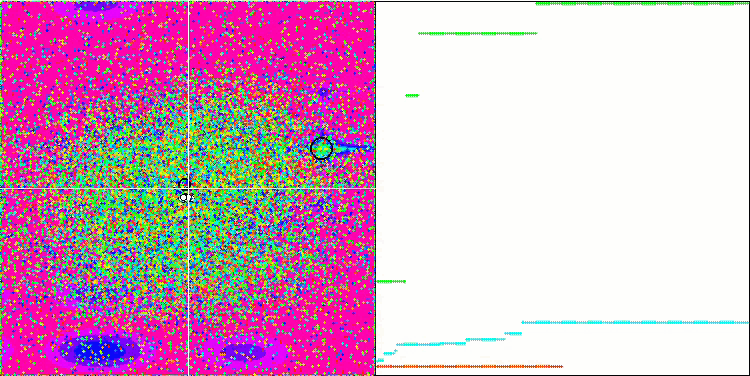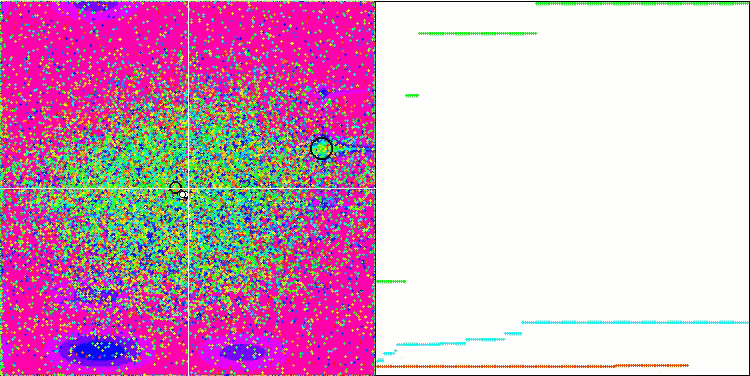
  메가시티 테스트 함수의 GWO

GWO 테스트 결과.

2022.11.28 13:24:09.370 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:24:14.895 Test_AO_GWO (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.914175888065222
2022.11.28 13:24:14.895 Test_AO_GWO (EURUSD,M1) 점수: 0.99900
2022.11.28 13:24:22.175 Test_AO_GWO (EURUSD,M1) 20 Skin's; Func 10000 실행 결과: 2.7419092435309405
2022.11.28 13:24:22.175 Test_AO_GWO (EURUSD,M1) 점수: 0.48033
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 1.5227848592798188
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) 점수: 0.18924
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:25:06.924 Test_AO_GWO (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.4822580151819842
2022.11.28 13:25:06.924 Test_AO_GWO (EURUSD,M1) 점수: 0.83844
2022.11.28 13:25:14.551 Test_AO_GWO (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 0.15477395149266915
2022.11.28 13:25:14.551 Test_AO_GWO (EURUSD,M1) 점수: 0.08755
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.04517298232457319
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) 점수: 0.02555
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:26:02.305 Test_AO_GWO (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 12.0
2022.11.28 13:26:02.305 Test_AO_GWO (EURUSD,M1) 점수: 1.00000
2022.11.28 13:26:09.475 Test_AO_GWO (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 1.2
2022.11.28 13:26:09.475 Test_AO_GWO (EURUSD,M1) 점수: 0.10000
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.2624
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) 점수: 0.02187
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) C_AO_GWO의 모든 점수: 0.41577484361261224

회색 늑대 최적화 알고리즘(GWO)은 회색 늑대 무리의 시뮬레이션 사냥을 기반으로 한 생물학에서 영감을 얻은 최적화 알고리즘 중 하나입니다. 이 알고리즘은 극한값을 찾는 정확도와 수렴 속도 측면에서 다양한 유형의 함수들 중에서 평균적으로 매우 효율적이라고 입증되었습니다. 일부의 테스트에서는 최고로 판명되었습니다. "회색 늑대" 최적화 알고리즘의 주요 성능 지표는 생물학적 알고리즘에서 영감을 얻은 최적화 알고리즘 클래스에서 "전통적"으로 여겨지는 파티클 스웜 최적화 알고리즘의 성능 지표보다 우수합니다.

동시에 회색 늑대 최적화 알고리즘의 계산의 복잡도는 파티클 스웜 최적화 알고리즘과 비슷합니다. GWO 최적화 알고리즘의 많은 장점으로 인해 알고리즘이 처음 발표된 이후 알고리즘을 수정하는 많은 작업이 등장했습니다. 알고리즘의 유일한 단점은 포레스트 샤프-최대 함수의 발견 좌표의 정확도가 낮다는 것입니다.

발견된 극값의 낮은 정확도는 포레스트 함수의 모든 차원에서 나타났으며 결과는 표의 모든 비교 대상 중에서 최악이었습니다. 이 알고리즘은 특히 크기가 큰 스킨 함수의 경우 평활화된 스킨 함수에서 효율적인 것으로 입증되었습니다. GWO는 또한 메가시티 함수에서 글로벌 최대치 100%를 달성한 3위에 올랐습니다.

AO

설명

피부

숲

메가시티(개별)

최종 결과

2 params(1 F)

40 params(20F)

1000 params(500 F)

2 params(1 F)

40 params(20F)

1000 params(500 F)

2 params(1 F)

40 params(20F)

1000 params(500 F)

ACOm

개미 군집 최적화

0.98229

0.79108

0.12602

1.00000

0.62077

0.11521

0.38333

0.44000

0.02377

0.49805222

ABCm

인공 꿀벌 군집 M

1.00000

0.63922

0.08076

0.99908

0.20112

0.03785

1.00000

0.16333

0.02823

0.46106556

ABC

인공 꿀벌 군집

0.99339

0.73381

0.11118

0.99934

0.21437

0.04215

0.85000

0.16833

0.03130

0.46043000

GWO

회색 늑대 최적화

0.99900

0.48033

0.18924

0.83844

0.08755

0.02555

1.00000

0.10000

0.02187

0.41577556

PSO

파티클 스웜 최적화

0.99627

0.38080

0.05089

0.93772

0.14540

0.04856

1.00000

0.09333

0.02233

0.40836667

RND

랜덤

0.99932

0.44276

0.06827

0.83126

0.11524

0.03048

0.83333

0.09000

0.02403

0.38163222


결론:

장점:
1. 빠른 속도.
2. 많은 변수가 있는 함수를 원활하게 처리할 수 있는 높은 수렴도를 제공합니다.

단점:
1. 보편적이지 않습니다.
2. 지역적 극한 상황에 갇히게 됩니다.
3. 개별적이고 차별화할 수 없는 함수에 대해 확장성이 낮습니다.


MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/11785

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기
모집단 최적화 알고리즘: 뻐꾸기 최적화 알고리즘(COA) 모집단 최적화 알고리즘: 뻐꾸기 최적화 알고리즘(COA)
다음으로 살펴볼 알고리즘은 레비 비행을 사용한 뻐꾸기 검색 최적화입니다. 이는 최신의 최적화 알고리즘 중 하나이며 인기 있는 새로운 알고즘 중 하나입니다.
VIDYA으로 트레이딩 시스템 설계하는 방법 알아보기 VIDYA으로 트레이딩 시스템 설계하는 방법 알아보기
가장 인기 있는 보조지표로 트레이딩 시스템을 설계하는 방법을 알아보는 이 시리즈의 새로운 글에 오신 것을 환영합니다. 이번 글에서는 새로운 보조지표 도구에 대해 알아보고 가변 지수 동적 평균(VIDYA)으로 트레이딩 시스템을 설계하는 방법을 배워보겠습니다.
디마커로 트레이딩 시스템 설계하는 방법 알아보기 디마커로 트레이딩 시스템 설계하는 방법 알아보기
다음은 가장 인기 있는 보조 지표로 트레이딩 시스템을 설계하는 방법에 대한 시리즈의 새 글입니다. 이 글에서는 디마커 지표로 트레이딩 시스템을 만드는 방법을 소개합니다.
불스 파워로 트레이딩 시스템 설계 하는 방법 알아보기 불스 파워로 트레이딩 시스템 설계 하는 방법 알아보기
이번 글은 가장 인기 있는 보조지표로 트레이딩 시스템을 설계하는 방법을 알아보는 시리즈의 새로운 글입니다. 이번에는 불스 파워 보조지표로 트레이딩 시스템을 설계하는 방법에 대해 알아봅니다.