MetaTrader 5 / 예
English Русский 中文 Español Deutsch 日本語 Português
preview
모집단 최적화 알고리즘: 박테리아 먹이 채집 최적화(BFO)

모집단 최적화 알고리즘: 박테리아 먹이 채집 최적화(BFO)

MetaTrader 5 — 예 | 8 11월 2024, 14:40
93 0
Andrey Dik
Andrey Dik

콘텐츠

1. 소개
2. 알고리즘에 대한 설명
3. 테스트 결과


1. 소개

박테리아 먹이 채집 최적화(BFO) 알고리즘은 매우 복잡하거나 불가능한 수치 함수 최대화/최소화 문제에 대한근사 솔루션을 찾는 데 사용할 수 있는 흥미로운 최적화 기법입니다. 이 알고리즘은 분산 최적화 및 제어를 위한 글로벌 최적화 알고리즘의 하나로 널리 알려져 있습니다. BFO는 대장균의 사회적 먹이 채집 행동에서 영감을 받았습니다. BFO는 여러 응용 분야에서 발생하는 실제 최적화 문제를 해결하는 데 효과적이라는 점에서 연구자들의 주목을 받고 있으며 대장균의 먹이 사냥 전략 이면의 생물학이 원래 방식 그대로 에뮬레이션 되고 간단한 최적화 알고리즘으로 사용됩니다.

대장균이나 살모넬라균과 같은 박테리아는 지구상에서 가장 성공적인 유기체 중 하나입니다. 이 민첩한 박테리아는 편모라는 반강체 부속물을 가지고 있으며 이 부속물을 이용해 몸을 비틀어 추진합니다. 모든 편모가 시계 반대 방향으로 회전하면 프로펠러 효과가 발생하여 박테리아가 어느 정도 직선 방향으로 이동합니다. 이 경우 박테리아는 수영이라는 동작을 수행합니다. 모든 편모는 같은 방향으로 회전합니다.

편모는 대장균 박테리아가 먹이를 찾는 동안 수행하는 두 가지 주요 작업인 회전과 유영을 가능하게 합니다. 편모가 시계 방향으로 회전하면서 각 편모는 세포를 밀어냅니다. 편모가 다른 방향으로 회전하면 박테리아가 넘어집니다. 박테리아는 유리한 환경에서는 덜 넘어지면서 이동하지만 유해한 환경에서는 영양분을 찾기 위해 자주 넘어집니다. 편모가 시계 반대 방향으로 움직일 경우 이는 박테리아가 매우 빠른 속도로 헤엄치는 데 도움이 됩니다.

위의 알고리즘에서 박테리아의 행동은 환경의 화학적 자극에 대한 미생물의 운동 반응인 박테리아적 화학 작용이라는 메커니즘에 의해 결정됩니다. 이 메커니즘을 통해 박테리아는 유인제(대부분 영양소)를 향해 이동하고 기피제(박테리아에 잠재적으로 해로운 물질)를 피해 이동합니다. 유인제와 기피제를 감지하는 수용체는 박테리아의 극에 위치합니다.

박테리아는 크기가 작기 때문에 극과 극 사이의 유용한 물질과 유해한 물질의 농도의 차이를 포착할 수 없습니다. 박테리아는 이동 중 농도 변화를 측정하여 이러한 물질의 경사를 결정합니다. 이 움직임의 속도는 초당 수십 개의 박테리아 길이에 달할 수 있습니다. 예를 들어 대장균은 보통 초당 길이의 10~20배의 속도로 움직입니다.


parent_clone

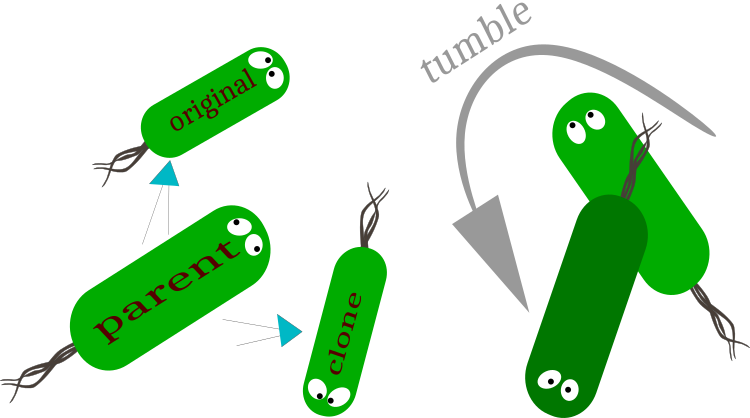
그림 1. 복제: 원본(동작 벡터 보존)과 복제(동작 벡터 변경) 박테리아로 나뉩니다.
텀블 - 박테리아 모션 벡터의 변화

박테리아가 선택한 이동 방향이 유인제의 농도 증가(기피제 농도 감소)와 같다면 다음 넘어질 때까지의 시간이 증가합니다. 박테리아의 크기가 작기 때문에 그 움직임은 브라우니안 운동의 영향을 많이 받습니다. 그 결과 박테리아는 평균적으로 유익한 물질을 향하고 유해한 물질을 멀리하는 방향으로만 이동합니다.

박테리아 이동에서 살펴본 메커니즘이 유일한 것은 아닙니다. 일부 박테리아는 편모가 하나뿐입니다. 이 경우 박테리아 이동의 변형으로는 다양한 회전 및 정지 모드가 있습니다. 그러나 어느 경우이던 박테리아가 올바른 방향으로 움직이면 그러한 움직임의 지속 시간이 증가합니다. 따라서 일반적으로 박테리아 화학 작용은 수영과 텀블링의 복잡한 조합으로 정의할 수 있으며 이를 통해 박테리아는 영양분 농도가 높은 곳에 머무르고 받아 들이기 힘든 농도의 유해 물질을 피할 수 있습니다.

검색 엔진 최적화 문제의 맥락으로 보면 박테리아 화학주성은 박테리아가 알려진 식량 자원의 사용을 최적화하고 잠재적으로 더 가치 있는 새로운 영역을 탐색하는 메커니즘으로 해석할 수도 있으며 충분한 양의 박테리아 집단은 복잡한 시공간적 구조를 형성할 수 있는데 이는 박테리아 집단에서 구조 형성의 효과라고 할 수 있습니다. 이 효과는 화학 작용과 다른 여러 가지 이유로 인해 생길 수 있습니다.

일부 박테리아의 경우 이러한 구조의 형성은 대사 산물의 조절 특성으로 설명됩니다. 자기력(자기장에 대한 민감도), 생체 대류, 음의 주지성(중력 방향에 대한 미생물의 우선적 이동) 및 기타 현상을 기반으로 유사한 효과를 얻을 수 있습니다. 일반적으로 박테리아는 친근한 환경에서 더 먼 거리를 이동합니다. 충분한 먹이를 얻으면 길이가 길어지고 적절한 온도가 주어지면 중간에서 부러져 자신의 정확한 복제품으로 변합니다.

이 현상을 보고 파시노는 복재 이벤트를 BFO에 도입하게 되었습니다. 갑작스러운 환경 변화나 공격으로 인해 화학 작용 과정이 중단되고 박테리아 그룹이 다른 곳으로 이동할 수 있습니다. 이는 실제 박테리아 집단에서 해당 지역의 모든 박테리아가 죽거나 박테리아 그룹이 환경의 새로운 부분으로 분산되는 제거 및 분산의 이벤트를 나타냅니다. 또한 살펴본 화학 작용 및 번식의 과정은 일반적으로 박테리아가 발견한 이 함수의 국소 최대 값을 벗어나는 것을 허용하지 않기 때문에 다중 극한 객관적 함수의 글로벌 최대 값을 찾는 데 불충분합니다. 제거 및 분산 절차는 이러한 단점을 극복하기 위해 고안되었습니다. 자연 선택(적자생존)에 따르면 체력이 약한 박테리아는 파괴되고 체력이 높은 박테리아는 스스로 번식하게 됩니다.


2. 알고리즘에 대한 설명

BFO의 정식 버전에는 다음과 같은 주요 단계가 포함되어 있습니다:

  1. 박테리아 군집을 초기화합.
  2. 화학주성.
  3. 군집.
  4. 복제.
  5. 청산 및 제거.

      
1. 매개변수 초기화하기.
박테리아는 일부 반고체 영양소에서는 복잡하고 안정적인 시공간적 패턴을 형성할 수 있습니다. 그리고 처음에 중앙에 함께 배치되면 환경내에서 생존할 수 있습니다. 또한 특정 조건에서는 세포 간 유인 신호를 분비하여 서로 뭉쳐서 서로를 보호합니다.
2. 화학주성.
먹이를 찾는 박테리아의 이동 특성은 두 가지 방법으로 결정할 수 있습니다. 함께 헤엄치고 텀블링하는 것을 화학 주성이라고 합니다. 박테리아는 올바른 방향으로 이동하면 '헤엄'치고 환경이 악화되는 방향으로 이동하면 '텀블링'한다고 합니다.


3. 군집.
박테리아가 가장 먹이가 풍부한 장소에 도달하기 위해서는 탐색 기간의 특정 시점까지 최적의 박테리아가 다른 박테리아를 유인하여 원하는 장소에서 더 빨리 함께 모이도록 해야 합니다. 이를 위해 각각의 박테리아에는 최적 박테리아와 이 검색 기간까지의 상대적 거리에 따라 원래 비용 함수에 페널티 함수가 추가됩니다. 마지막으로 모든 박테리아가 결정 지점에 합쳐지면 이 페널티 함수는 0이 됩니다. 군집화의 효과는 박테리아가 집단으로 모여 동심원의 패턴으로 이동하면서 박테리아 밀도가 높아지게 되는 것입니다.


4. 복제.
여러 화학적 단계를 통과한 초기 박테리아 세트는 번식 단계에 도달합니다. 여기서 최고의 박테리아 세트는 두 그룹으로 나뉩니다. 건강한 절반은 먹이를 찾는 능력이 떨어져 파괴되는 나머지 절반의 박테리아로 대체됩니다. 이를 통해 진화 과정에서 박테리아의 개체수를 일정하게 유지합니다.


5. 제거 및 분산.
진화하는 동안에는 예상치 못한 갑작스러운 사건이 발생하여 원활한 진화 과정이 크게 바뀌고 많은 박테리아가 제거되거나 새로운 환경으로 분산될 수 있습니다. 아이러니하게도 이 알려지지 않은 사건은 박테리아의 정상적인 화학적 성장을 방해하는 대신 새로운 박테리아를 음식이 있는 곳에 더 가깝게 배치할 수 있습니다. 넓은 관점에서 볼 때 제거와 분산은 장거리 이동을 하는 모집단의 행동의 일부입니다. 최적화에 적용하면 이러한 병렬 검색 알고리즘에서 흔히 볼 수 있는 정체를 줄이는 데 도움이 됩니다.

제가 구현한 BFO는 정식 버전과 약간 다릅니다. 코드의 특정 섹션을 통해 이러한 변경의 필요성에 대한 근거와 함께 차이점에 대해 자세히 설명하겠습니다. 일반적으로 구현에서의 변경 사항은 중요한 것으로 간주될 수 없으므로 알고리즘 이름에 "m"(수정 버전) 마커를 지정하지 않습니다. 저는 변경 사항을 적용하여 결과가 개선되었다는 점만 알려드리겠습니다.

다음으로 제가 구현한 알고리즘과 코드를 살펴보겠습니다.

알고리즘 단계:

1. 박테리아 식민지 초기화.
2. 박테리아 건강(피트니스) 측정.
3. 복제?
3.1. 예. 복제를 수행합니다.
3.2. 아니요. p.4.
4. 오래됨(수명 제한 도달)?
4.1. 예. 텀블을 수행합니다(이동 벡터 변경).
4.2. 아니요. p.5.
5. 올바른 방향으로 나아가고 있나요?
5.1. 예. 동일한 벡터로 계속 이동합니다.
5.2. 아니요. 텀블을 수행합니다(이동 벡터 변경).
6. 박테리아 상태(건강도)를 측정합니다.
7. 정지 기준이 충족될 때까지 p. 3를 계속 진행.

알고리즘의 논리적 체계는 그림 1에 나와 있습니다.


cheme

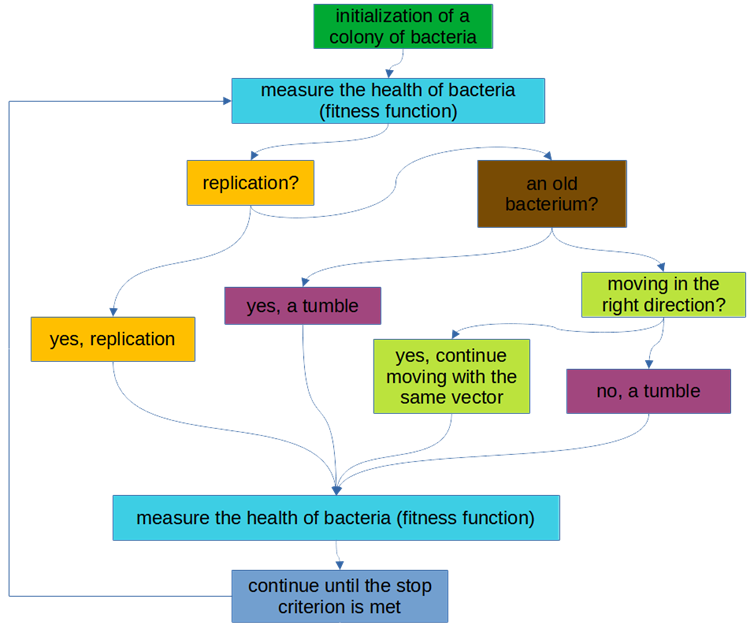
그림 2. BFO 알고리즘 로직 블록 다이어그램

코드를 살펴보겠습니다.

박테리아를 설명하는 가장 좋은 방법은 좌표 배열과 모션 벡터를 포함하는 구조를 통해서입니다. 박테리아의 현재 및 이전 건강 수치와 생명력 카운터. 본질적으로 생명 카운터는 생명 한계에 도달하면 박테리아가 파괴되고 검색 공간의 임의의 위치에 새로운 박테리아가 생성되는 원래 버전과 달리 한 방향으로 순차적으로 이동하는 양을 제한하는 데 필요합니다. 그러나 이전 글에서 이미 이 주제에 대해 다루었으므로 임의의 위치에 새로운 에이전트를 만드는 것은 실질적인 의미가 없으며 검색 기능만 악화시킬 뿐입니다. 이 경우 최적의 솔루션 위치에 새로운 에이전트를 만들거나 현재 위치에서 계속 이동하되 방향 벡터를 변경하는 것이 좋습니다. 두 번째 옵션이 더 나은 결과를 보여주었습니다.

표준 버전은 일정한 모션 벡터를 사용합니다. 생명체가 많으면 검색 공간에서 박테리아가 일직선을 따라 이동하게 됩니다. 이 선이 극한을 더 잘 통과하지 못하면 이 직선 운동의 과정이 무한히 발생하지만 여기서 카운터는 박테리아가 평생 동안 직선 운동을 피할 수 있도록 하는 강제 텀블 역할을 합니다. 경사가 없는 영역이 있는 함수에서는 결국 체력 향상을 시작할 수 있는 장소로 연결됩니다.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bacteria
{
  double c  [];   //coordinates
  double v  [];   //vector
  double f;       //current health
  double fLast;   //previous health
  double lifeCNT; //life counter
};
//——————————————————————————————————————————————————————————————————————————————

BFO 알고리즘 클래스를 C_AO_BFO로 선언해 보겠습니다. 클래스에는 박테리아 식민지 선언, 검색 공간의 경계, 최적 솔루션의 값, 최적 솔루션의 좌표 배열이 포함되어 있습니다. 또한 알고리즘 매개변수의 상수 값을 선언합니다.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BFO
{
  //----------------------------------------------------------------------------
  public: S_Bacteria b     []; //bacteria
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP);   //life counter

  public: void Swimming   ();
  public: void Evaluation ();

  //----------------------------------------------------------------------------
  private: double NewVector (int paramInd);
  private: S_Bacteria bT []; //bacteria
  private: double v      [];
  private: int    ind    [];
  private: double val    [];
  private: int    populationSize; //population size
  private: int    parameters;     //number of optimized parameters
  private: double lambda;         //lambda
  private: double reproduction;   //probability of reproduction
  private: int    lifeCounter;    //life counter
  private: bool   evaluation;

  private: void   Sorting ();
  private: double SeInDiSp             (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

공용 Init () 메서드는 상수 변수를 초기화하고, 배열 크기를 분배하고, 플래그와 최적 솔루션의 값을 재설정하는 데 사용됩니다.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP)    //life counter
{
  fB = -DBL_MAX;
  evaluation = false;

  parameters      = paramsP;
  populationSize  = populationSizeP;
  lambda          = lambdaP;
  reproduction    = reproductionP;
  lifeCounter     = lifeCounterP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);
  ArrayResize (v,         parameters);

  ArrayResize (ind,       populationSize);
  ArrayResize (val,       populationSize);

  ArrayResize (b,  populationSize);
  ArrayResize (bT, populationSize);

  for (int i = 0; i < populationSize; i++)
  {
    ArrayResize (b [i].c,  parameters);
    ArrayResize (b [i].v,  parameters);
    b [i].f  = -DBL_MAX;
    b [i].fLast = -DBL_MAX;

    ArrayResize (bT [i].c,  parameters);
    ArrayResize (bT [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

각각의 반복마다 호출해야 하는 첫 번째 공개 메서드인 Swimming () 또는 박테리아 수영에는 알고리즘의 모든 주요 로직이 포함되어 있습니다. 

void C_AO_BFO::Swimming ()
{}

방법을 자세히 살펴보겠습니다. 첫 번째 반복에서 평가 플래그가 'false'로 설정되면 우리는 전체 검색 공간에 균일한 분포로 박테리아를 무작위로 흩뿌립니다. 이 단계에서는 현재 상태(피트니스)와 이전 상태를 알 수 없습니다. 해당 변수에 DBL_MAX 값을 할당해 보겠습니다. 경계를 넘어가기 위해 무작위로 얻은 좌표를 확인하고 최적화된 매개변수를 변경하는 단계를 적용합니다. 이 반복에서 각 박테리아에 대한 개별 변위 벡터를 NewVector () 비공개 메서드를 사용하여 설정해야 합니다(아래에서 살펴볼 것입니다). 모든 박테리아는 변화의 조건이 충족될 때까지 동일한 개별 벡터를 가지고 일직선으로 동일하게 앞으로 헤엄칩니다. 

//----------------------------------------------------------------------------
if (!evaluation)
{
  fB = -DBL_MAX;

  for (int s = 0; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);

      v [k] = rangeMax [k] - rangeMin [k];

      b [s].v [k] = NewVector (k);

      b [s].f  = -DBL_MAX;
      b [s].fLast = -DBL_MAX;

      b [s].lifeCNT = 0;
    }
  }

  evaluation = true;
}

두 번째 및 후속 반복에서는 생존의 한계에 도달하면 박테리아의 수영, 텀블링, 복제 및 파괴 작업이 수행됩니다. 로직의 첫 번째는 매개변수에 지정된 확률로 재생산하는 작업입니다. 이는 이전 반복에서 박테리아 군집이 건강 값의 내림차순으로 정렬되었다는 것을 의미합니다.

알고리즘의 번식은 박테리아 군집의 '유전자 풀'을 개선하여 알고리즘의 수렴을 가속화하는 중요한 기능을 수행합니다. 이 작업은 박테리아를 가상의 두 부분으로 나누는 것으로 식민지의 첫 번째 더 나은 절반만 분열이 허용됩니다. 식민지의 전반부는 절반으로 줄어들고 원래의 부모 버전은 식민지의 후반부에 배치됩니다. 부모 박테리아는 복제 박테리아와는 반대로 동일한 벡터를 사용하여 계속 이동합니다. 복제는 식민지의 제자리에 남아 있게 되며 여기에는 새로운 이동 벡터가 할당됩니다. 부모와 그 복제본은 분할이 발생한 공간의 지점에서 계속 이동합니다.

r = RNDfromCI (0.0, 1.0);

//==========================================================================
if (r < reproduction)
{
  int st = populationSize / 2;
  for (int s = 0; s < st; s++)
  {
    //bacterium original--------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [st + s].v [k] = b [s].v [k];
      b [st + s].c [k] = b [s].c [k] + b [s].v [k];
      b [st + s].c [k] = SeInDiSp (b [st + s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [st + s].fLast = b [s].f;
      b [st + s].lifeCNT++;
    }

    //bacterium clone-------------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT = 0;
    }
  }
}

복제 확률이 구현되지 않으면 박테리아 수명 한계에 도달했는지 확인됩니다. 표준 버전의 알고리즘에서는 "오래된" 박테리아를 파괴하고 대신 박테리아 목록 내 검색 공간의 임의의 위치에 새로운 박테리아가 생성되어야 합니다. 일반적인 경우 생식 및 화학 축의 연산은 다음과 같은 이유로 다중 극한 적합성 함수의 전역 최대값을 찾는 데 충분하지 않습니다.
이러한 절차는 박테리아가 발견한 최소한의 지역 밖으로 나가는 것을 허용하지 않습니다. 청산 절차는 이러한 단점을 극복하기 위해 고안되었습니다. 그러나 이 알고리즘과 다른 알고리즘을 사용한 실험 사례에서 알 수 있듯이 이 경우에는 단순히 모션 벡터를 변경하는 것이 더 효율적입니다. 수명 카운터가 초기화됩니다. 카운터는 주어진 스텝 수(생명)가 지나면 이동 방향을 변경하는 트리거입니다. 복제와 제거의 결과로 나타나는 총 박테리아의 수는 일정하게 유지됩니다.

if (b [s].lifeCNT >= lifeCounter)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].v [k] = NewVector (k);
    b [s].c [k] = b [s].c [k] + b [s].v [k];
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    b [s].fLast = b [s].f;
    b [s].lifeCNT = 0;
  }
}

수명 제한이 소진되지 않은 경우 박테리아가 피트니스 함수의 기울기를 개선하기 위해 움직이고 있는지 확인합니다. 즉 우리는 현재 반복과 이전 반복에서 두 가지 상태 값을 확인합니다. 건강이 개선되면 모션 벡터가 보존되고 그렇지 않으면 박테리아가 텀블을 수행해야 합니다(모션 벡터 변경).

표준 버전에서는 현재 및 이전 상태 확인에 엄격하게 "보다 큰" 현재 및 이전 상태 확인을 수행하는 반면 저의 버전에서는 "보다 크거나 같은"이 적용되어 수행 중인 표면의 완전히 "수평"섹션에서도 박테리아가 계속 이동할 수 있으며 그렇지 않으면 박테리아가 한 곳에서 끝없이 떨어집니다 (건강 상태의 변화가 없으므로 수영 방향이 없음을 의미 함). 우리는 이 단계에서 수신된 새 좌표가 검색 공간의 경계를 넘어 출력되는지도 확인해야 합니다.

else
{
  if (b [s].f >= b [s].fLast)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
  else
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
}

NewVecror () - 모션 벡터(텀블)를 변경하는 비공개 메서드입니다. 이 메서드는 각 좌표에 적용됩니다. 이 메서드는 해당 좌표 v에 대한 검색 경계 사이의 차이에 [-1.0;1.0] 범위의 난수 r을 곱하고 람다 배율(알고리즘 매개변수 중 하나)을 곱하는 간단한 방식입니다. 박테리아는 생명의 한계가 소진될 때까지(같은 장소에서 새로운 박테리아가 생성되지만 새로운 이동 벡터를 사용) 복제하는 동안(복제본에 새로운 벡터가 있음) 건강이 악화되는 동안(더 유리한 새로운 환경을 찾으려는 시도) 변경 없이 이동 벡터를 사용합니다.   

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BFO::NewVector (int paramInd)
{
  double r = RNDfromCI (-1.0, 1.0);
  return lambda * v [paramInd] * r;
}
//——————————————————————————————————————————————————————————————————————————————

각각의 반복마다 실행되어야 하는 두 번째 공개 Evaluation() 메서드는 정렬 메서드를 호출하고 정렬된 식민지에서 가장 좋은 박테리아의 상태를 가장 잘 찾은 솔루션과 비교하는 글로벌 솔루션의 업데이트를 확인합니다.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Evaluation ()
{
  Sorting ();

  if (b [0].f > fB)
  {
    fB = b [0].f;
    ArrayCopy (cB, b [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. 테스트 결과

BFO 테스트 스탠드 결과:

2023.01.21 12:52:46.501 Test_AO_BFO (.US500Cash,M1) C_AO_BFO:50;0.01;0.8;100
2023.01.21 12:52:46.501 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:52:48.451 Test_AO_BFO (.US500Cash,M1) 5 Rastrigin's; Func 10000 실행 결과: 72.94540549092933
2023.01.21 12:52:48.451 Test_AO_BFO (.US500Cash,M1) 점수: 0.90383
2023.01.21 12:52:51.778 Test_AO_BFO (.US500Cash,M1) 25 Rastrigin's; Func 10000 실행 결과: 54.75744312933767
2023.01.21 12:52:51.778 Test_AO_BFO (.US500Cash,M1) 점수: 0.67848
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) 500 Rastrigin's; Func 10000 실행 결과: 40.668487609790404
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) 점수: 0.50391
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:53:23.211 Test_AO_BFO (.US500Cash,M1) 5 Forest's; Func 10000 실행 결과: 0.8569098398505888
2023.01.21 12:53:23.211 Test_AO_BFO (.US500Cash,M1) 점수: 0.48471
2023.01.21 12:53:26.878 Test_AO_BFO (.US500Cash,M1) 25 Forest's; Func 10000 실행 결과: 0.37618151461180294
2023.01.21 12:53:26.878 Test_AO_BFO (.US500Cash,M1) 점수: 0.21279
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) 500 Forest's; Func 10000 실행 결과: 0.08748190028975696
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) 점수: 0.04948
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:54:28.849 Test_AO_BFO (.US500Cash,M1) 5 Megacity's; Func 10000 실행 결과: 4.8
2023.01.21 12:54:28.849 Test_AO_BFO (.US500Cash,M1) 점수: 0.40000
2023.01.21 12:54:40.089 Test_AO_BFO (.US500Cash,M1) 25 Megacity's; Func 10000 실행 결과: 2.216
2023.01.21 12:54:40.089 Test_AO_BFO (.US500Cash,M1) 점수: 0.18467
2023.01.21 12:55:24.640 Test_AO_BFO (.US500Cash,M1) 500 Megacity's; Func 10000 실행 결과: 0.4232
2023.01.21 12:55:24.640 Test_AO_BFO (.US500Cash,M1) 점수: 0.03527

명확한 결론을 내리기에는 너무 이릅니다. 먼저 다른 테스트 참가자들과 비교하여 결과를 분석할 필요가 있습니다.

rastrigin

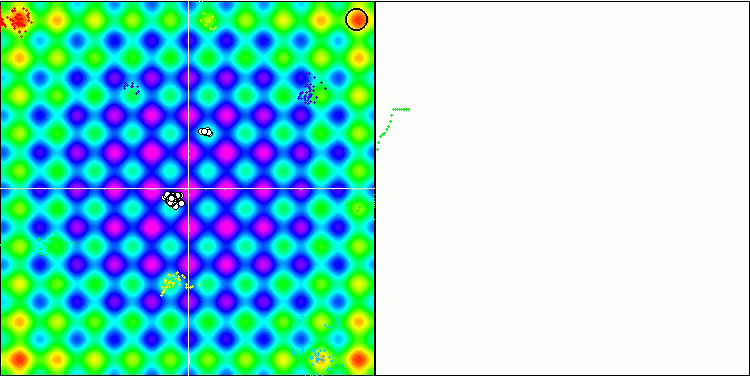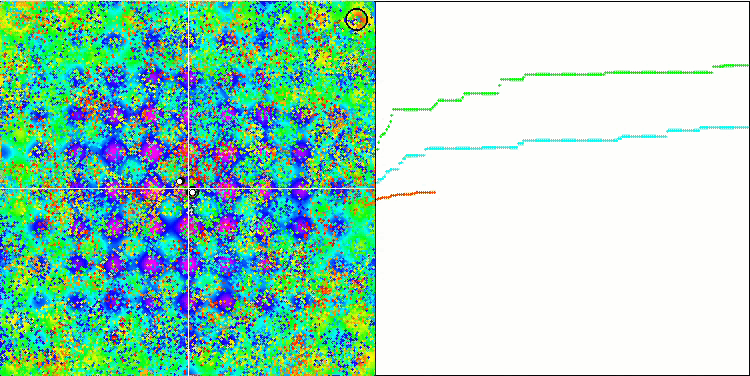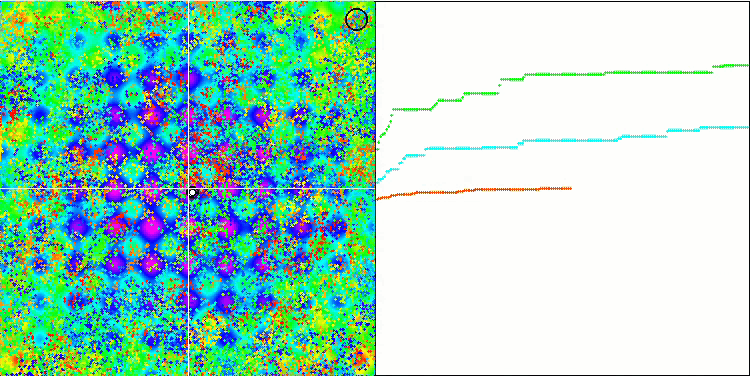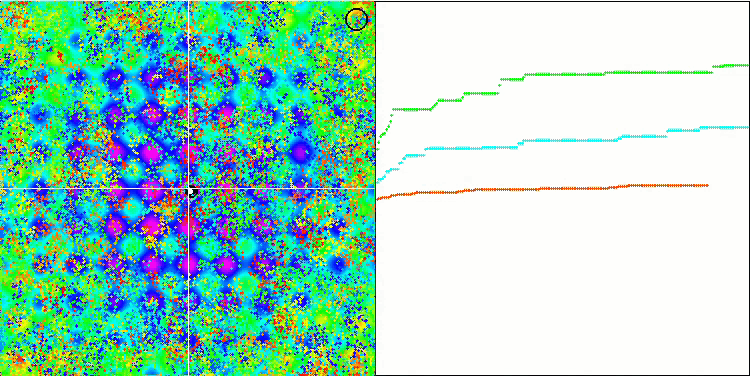
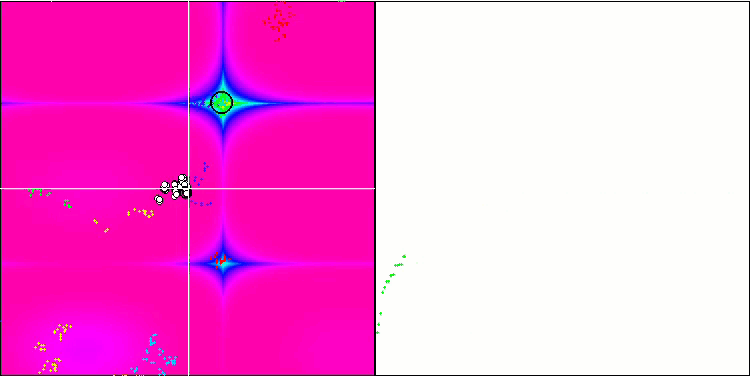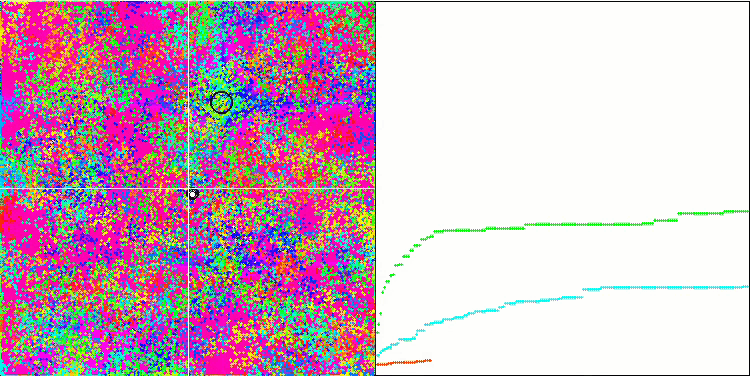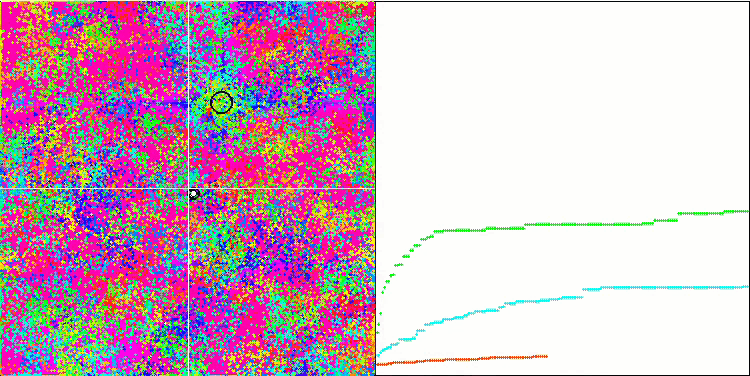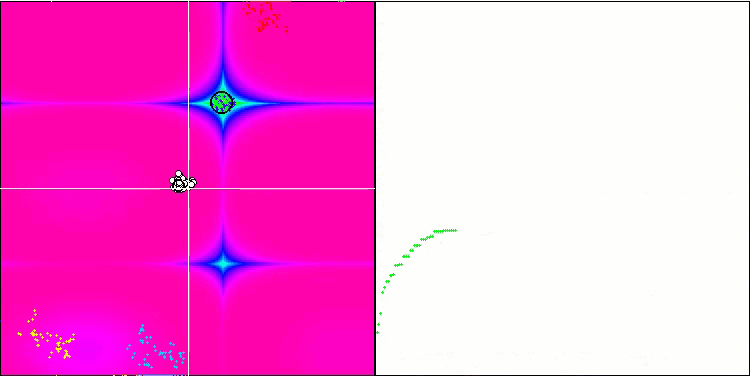
  Rastrigin 테스트 기능에 대한 BFO.

숲

BFO 의 Forest 테스트 기능.

메가시티

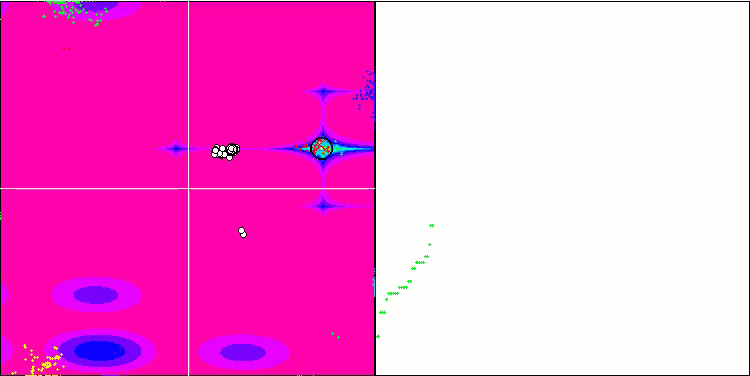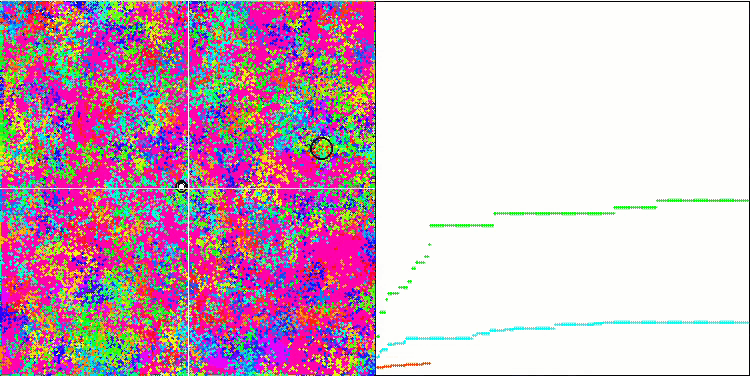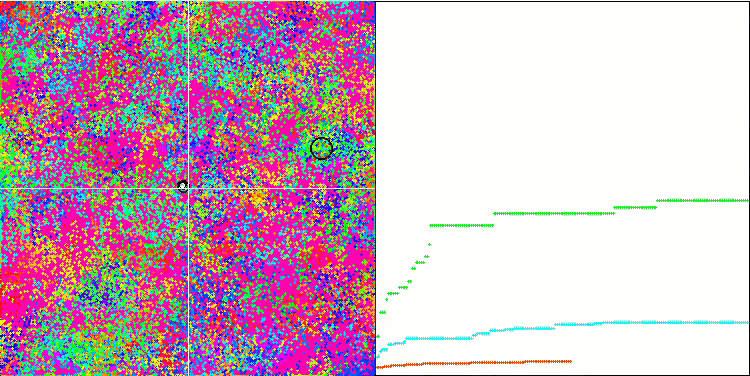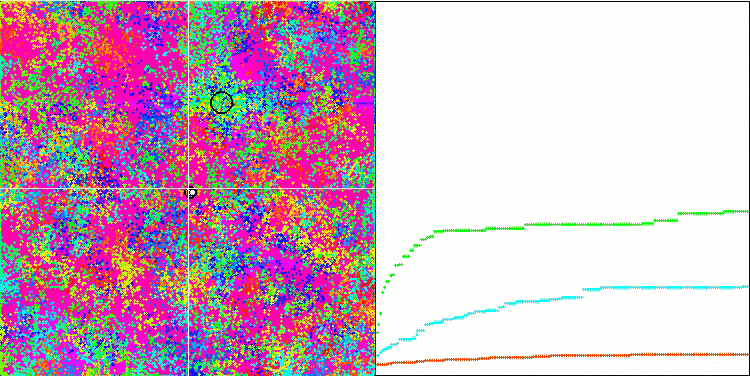
BFO 의 메가시티 테스트 기능.

테스트 시각화에 주목해 보겠습니다. 애니메이션을 통해 확인해 보면 알고리즘에서 '보다 큼' 기호를 '보다 크거나 같음'으로 대체하기로 한 결정이 옳았음을 확인할 수 있었습니다. 이를 통해 박테리아는 테스트 함수의 수평 섹션에서 계속 움직일 수 있었습니다. 이는 특히 숲과 메가시티 함수에서 두드러집니다. 박테리아는 함수 경사가 전혀 없는 곳에서도 계속 움직이려고 합니다. 또한 알고리즘에는 하위 식민지 형성을 위한 논리적 방법이 포함되어 있지 않지만 박테리아 식민지가 시각적으로 별도의 지역 극단으로 나뉘어 여러 개의 개별 식민지로 분할되는 능력에 주목할 필요가 있으며 이는 분명 긍정적인 특징으로 간주 될 수 있습니다. 일반적으로 검색 공간에서 박테리아의 균일한 움직임은 어느 방향 으로든 급격한 점프를 시도하지 않고도 눈에 띄며 이는 균일한 점진적 움직임인 화학 주성으로 설명됩니다.

AO

설명

Rastrigin

Rastrigin final

숲

숲 최종

메가시티(이산)

메가시티 최종

최종 결과

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

IWO

침입성 잡초 최적화

1.00000

1.00000

0.33519

2.33519

0.79937

0.46349

0.41071

1.67357

0.75912

0.44903

0.94088

2.14903

100.000

ACOm

개미 식민지 최적화 M

0.36118

0.26810

0.17991

0.80919

1.00000

1.00000

1.00000

3.00000

1.00000

1.00000

0.10959

2.10959

95.996

COAm

뻐꾸기 최적화 알고리즘 M

0.96423

0.69756

0.28892

1.95071

0.64504

0.34034

0.21362

1.19900

0.67153

0.34273

0.45422

1.46848

74.204

FAm

반딧불이 알고리즘 M

0.62430

0.50653

0.18102

1.31185

0.55408

0.42299

0.64360

1.62067

0.21167

0.28416

1.00000

1.49583

71.024

BA

박쥐 알고리즘

0.42290

0.95047

1.00000

2.37337

0.17768

0.17477

0.33595

0.68840

0.15329

0.07158

0.46287

0.68774

59.650

ABC

인공 꿀벌 군집

0.81573

0.48767

0.22588

1.52928

0.58850

0.21455

0.17249

0.97554

0.47444

0.26681

0.35941

1.10066

57.237

BFO

박테리아 먹이 채집 최적화

0.70129

0.46155

0.11627

1.27911

0.41251

0.26623

0.26695

0.94569

0.42336

0.34491

0.50973

1.27800

55.516

FSS

물고기 떼 검색

0.48850

0.37769

0.11006

0.97625

0.07806

0.05013

0.08423

0.21242

0.00000

0.01084

0.18998

0.20082

20.109

PSO

파티클 스웜 최적화

0.21339

0.12224

0.05966

0.39529

0.15345

0.10486

0.28099

0.53930

0.08028

0.02385

0.00000

0.10413

14.232

RND

랜덤

0.17559

0.14524

0.07011

0.39094

0.08623

0.04810

0.06094

0.19527

0.00000

0.00000

0.08904

0.08904

8.142

GWO

회색 늑대 최적화

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.18977

0.04119

0.01802

0.24898

1.000


이제 테스트 결과를 분석할 차례입니다. BFO는 현재 알고리즘 목록에서 전체 점수가 55점을 조금 넘으며 평가표의 중간에 위치해 있습니다. 결과가 인상적이지는 않지만 나쁘지도 않습니다. 특히 10개의 변수가 있는 Rastrigin 함수에서 좋은 결과를 얻었습니다. 50개와 1000개의 변수가 있는 경우 결과가 눈에 띄게 나빠집니다. 또한 알고리즘이 숲 함수에서 제대로 작동하지 않았습니다. 알고리즘에 이러한 함수에 대한 작업 메커니즘이 없습니다. 그럼에도 이산형 메가시티 함수에 대한 비교적 양호한 동작은 놀랍습니다. 또한 다른 알고리즘에 비해 확장성이 뛰어납니다(1000개의 메가시티 매개변수로 테스트).

BFO는 다양한 가능성을 가진 과학 분야입니다. 최적화 성능을 향상시키기 위해 모델링할 수 있는 박테리아 먹이 채집 및 동물 먹이 채집에는 일반적으로 여러 가지 측면이 있습니다. BFO 알고리즘의 경우 매개변수가 많기 때문에 제어 매개변수를 자동으로 조정하는 것이 특히 중요할 수 있으며 이를 통해 향상된 성능을 발휘할 수 있으며 이 부분은 추가적인 실험이 필요한 부분입니다.

BFO는 초기화 및 매개변수 선택 시 좌표의 초기값에 대한 낮은 민감도, 우수한 신뢰성, 논리의 단순성, 구현의 용이성, 병렬화 및 전역 검색이 가능한 점 등 여러 가지 장점이 있습니다. 이러한 이유로 BFO 알고리즘은 다양한 최적화 문제를 해결하는 데 사용됩니다. 그러나 BFO는 느린 수렴, 경우에 따라 로컬 최적값을 초과할 수 없음, 고정된 스텝 길이 등 여러 가지 단점도 가지고 있습니다. BFO는 메타 휴리스틱으로 알고리즘 수정을 개발하는 데 사용할 수 있는 개념적 프레임워크에 불과합니다. 여기서 제가 소개한 BFO 버전은 여러 가지 가능성들 중의 하나일 뿐이며 이 주제에 대한 최종 결론이 아니라 실험의 출발점으로 보아야 합니다.

알고리즘 테스트 결과의 히스토그램은 아래에 나와 있습니다.

차트

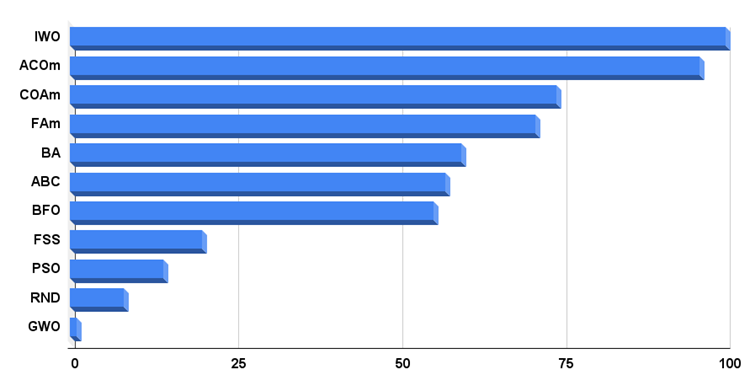
그림 3. 테스트 알고리즘의 최종 결과 히스토그램

박테리아 먹이 채집 최적화(BFO) 알고리즘의 속성에 대한 결론:

장점:
1. 빠른 속도.
2. 간단한 논리.
3. 느리긴 하지만 모든 반복에 걸쳐 수렴.

단점:
1. 느린 컨버전스.
2. 로컬 극한을 종료하는 방법이 없음.


MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/12031

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기
새로운 기능: MQL5의 커스텀 인디케이터 새로운 기능: MQL5의 커스텀 인디케이터
MetaTrader5와 MQL5의 새로운 기능 전체를 나열하지는 않겠습니다. 종류도 많은 데다가, 별도의 설명이 필요한 기능들도 있거든요. 객체 지향 프로그래밍을 이용한 코드 작성법 또한 다음에 알아보도록 하겠습니다. 다른 기능들과 함께 설명하기에는 조금 어려운 이야기일 수 있으니까요. 이 글에서는 인디케이터와 인디케이터의 구조, 드로잉 타입과 프로그래밍 디테일을 MQL4와 비교해 볼게요. 초보자 분들께 많은 도움이 되면 좋겠고 기존에 사용하시던 개발자 분들도 뭔가 새로운 걸 얻어 가실 수 있길 바랍니다.
예제로 패턴 살펴보기(1부): 멀티 탑 예제로 패턴 살펴보기(1부): 멀티 탑
이번 글은 알고리즘 트레이딩 프레임워크의 반전 패턴과 관련된 시리즈의 첫 번째 글입니다. 더블 탑과 더블 바텀 패턴에서 유래한 가장 흥미로운 패턴 계열부터 살펴보겠습니다.
새 MetaTrader 와 MQL5를 소개해드립니다 새 MetaTrader 와 MQL5를 소개해드립니다
본 문서는 MetaTrader5의 간략 리뷰입니다. 짧은 시간 내에 시스템의 모든 세부 사항을 안내해드리기는 어렵습니다 - 테스트는 2009.09.09에 시작되었습니다. 이는 상징적인 일자로, 전 이것이 행운의 숫자가 될거라 믿어 의심치않습니다. 제가 새 MetaTrader 5 터미널과 MQL5 베타버전을 받은지 며칠이 지났습니다. 아직 모든 기능을 사용해본 것은 아니지만, 벌써부터 감명깊네요.
스왑(1부): 잠금 및 합성 포지션 스왑(1부): 잠금 및 합성 포지션
이 기사에서 저는 스왑 거래 방법의 고전적인 개념을 확장하고자 합니다. 저는 이 개념이 특별한 관심을 기울일 가치가 있고 연구에 절대적으로 권장된다는 결론에 도달했습니다. 이제 그 이유를 설명하겠습니다.