理論から実践へ - ページ 521 1...514515516517518519520521522523524525526527528...1981 新しいコメント multiplicator 2018.09.02 23:33 #5201 ダッシュボードはどうしたんですか? グラフの平均値を表示します。マーク0からマーク10まで上昇したグラフの平均値はどうなるでしょうか? 5. つまり、今までの尺度は5になるわけです。グラフはすでに10になっているのに。 線形回帰が役に立ちます。 線形回帰線は価格チャネルの中心を通り、この線の最後のポイントは10になります。 しかし、チャンネルは常にまっすぐとは限りません。円弧状のチャネルもあります。この場合、LRはうまく機能しません。 そこで、多項式回帰が活躍する。 OR プロットはチャンネルの中心をまっすぐ進み、その最後のポイントもチャンネルの中心になります。 そして、そのような円弧に沿ってPRがどのように進むか(正弦波のスライスに忠実な場合)、次のようになります。 デメリットも考えないと...。 Maxim Dmitrievsky 2018.09.02 23:37 #5202 Smokchi Struck:ダッシュボードはどうしたんだ? グラフの平均値を表示します。マーク0からマーク10まで上昇したグラフの平均値はどうなるでしょうか? 5. つまり、今までの尺度は5になるわけです。グラフはすでに10になっているのに。 線形回帰が役に立ちます。 線形回帰線は価格チャネルの中心を通り、この線の最後のポイントは10になります。 しかし、チャンネルは必ずしもまっすぐではありません。円弧状のチャネルもあります。この場合、LRはうまく機能しません。 そこで、多項式回帰が活躍する。 PRグラフはチャンネルの中心をまっすぐ進み、その最終ポイントもチャンネルの中心になります。 ここで、もうひとつのアーク。(つまり正弦波のスライス)。 デメリットも考えないと...。 Violetta Novak 2018.09.02 23:38 #5203 Maxim Dmitrievsky:しかし、基本は同じで、カーネル変換を使って新しい次元にマッピングを導入することで依存関係を再構築し、その上にさらに別のものを追加しているのです ちなみに、Victorは確率 密度のカーネル推定に関する記事を掲載しています。https://www.mql5.com/ru/articles/396 multiplicator 2018.09.02 23:39 #5204 Maxim Dmitrievsky: 欠陥?) この方がもっといい。 それを解決する方法を考える。 Yuriy Asaulenko 2018.09.02 23:41 #5205 Maxim Dmitrievsky: 予測についてはどうでしょうか?)) Maxim Dmitrievsky 2018.09.02 23:41 #5206 Smokchi Struck: 欠陥?) それを解決する方法を考える。を今の次元で解決することはできない、それが問題なのです。あなたの回帰は、そのような事象が発生する可能性について何も知りません Maxim Dmitrievsky 2018.09.02 23:46 #5207 Novaja: ちなみに、ビクターはカーネル確率密度について、こちらの記事を掲載しています。https://www.mql5.com/ru/articles/396カーネルのトリックではなく、特徴ベクトルを他の空間にマッピングすることだと思うのですが 少なくとも私見では...未読です。 multiplicator 2018.09.02 23:49 #5208 Maxim Dmitrievsky:を今の次元で解決することはできない、それが問題なのです。あなたの回帰は、そのような事象が発生する可能性について何も知りません まあ、そのために私たちはここにいるわけで、問題を解決するためにね)) Maxim Dmitrievsky 2018.09.02 23:50 #5209 Smokchi Struck: 欠点?) こんな感じです。 それを解決する方法を考える。通常はこのようなものです。 multiplicator 2018.09.02 23:51 #5210 Maxim Dmitrievsky:を今の次元で解決することはできない、それが問題なのです。あなたの回帰は、そのような事象が発生する可能性について何も知りません グラフを1点刻みで表示することもできます。 グラフが1点上がった→1点刻みを上に、グラフが1点下がった→1点刻みを下に、とすると、点数がたくさん出てきます。 1...514515516517518519520521522523524525526527528...1981 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
ダッシュボードはどうしたんですか?


グラフの平均値を表示します。マーク0からマーク10まで上昇したグラフの平均値はどうなるでしょうか?
5.
つまり、今までの尺度は5になるわけです。グラフはすでに10になっているのに。
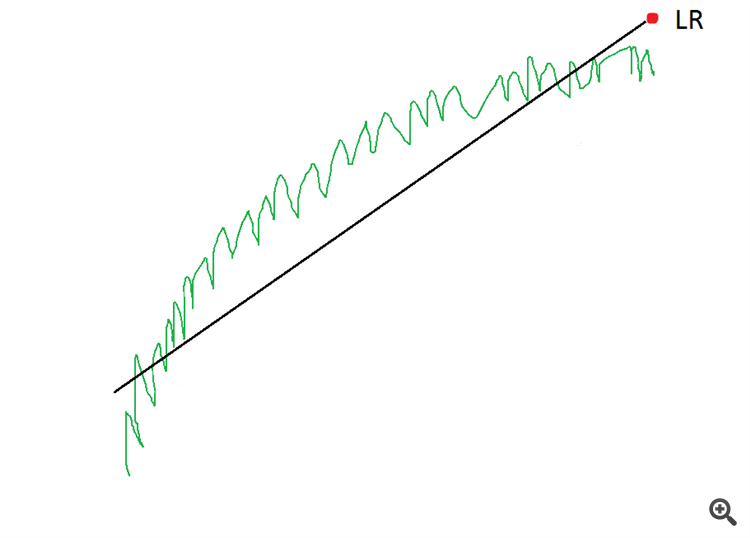
線形回帰が役に立ちます。
線形回帰線は価格チャネルの中心を通り、この線の最後のポイントは10になります。
しかし、チャンネルは常にまっすぐとは限りません。円弧状のチャネルもあります。この場合、LRはうまく機能しません。
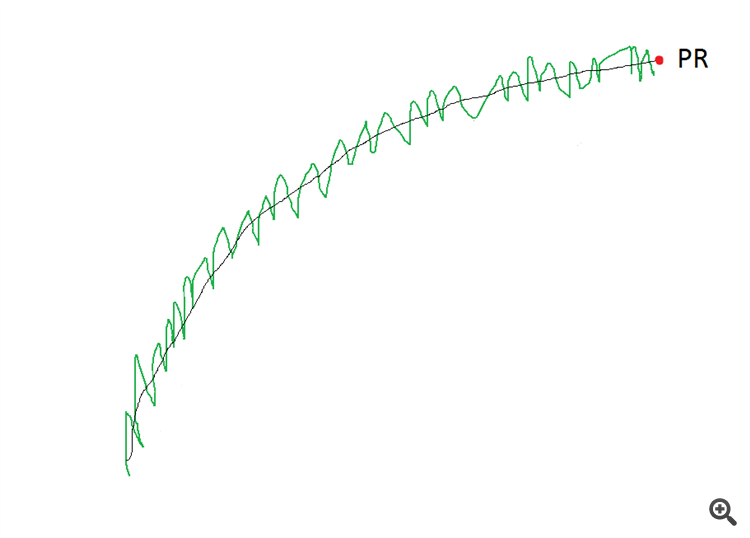
そこで、多項式回帰が活躍する。
OR プロットはチャンネルの中心をまっすぐ進み、その最後のポイントもチャンネルの中心になります。
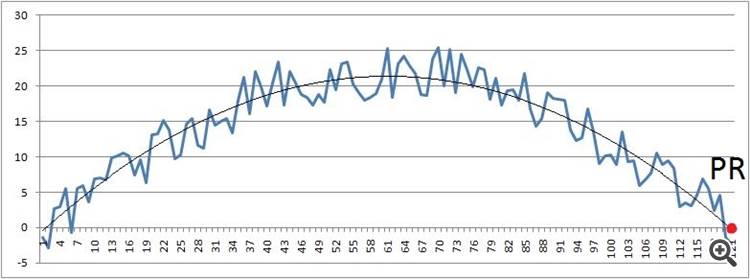
そして、そのような円弧に沿ってPRがどのように進むか(正弦波のスライスに忠実な場合)、次のようになります。
デメリットも考えないと...。
ダッシュボードはどうしたんだ?
グラフの平均値を表示します。マーク0からマーク10まで上昇したグラフの平均値はどうなるでしょうか?
5.
つまり、今までの尺度は5になるわけです。グラフはすでに10になっているのに。
線形回帰が役に立ちます。
線形回帰線は価格チャネルの中心を通り、この線の最後のポイントは10になります。
しかし、チャンネルは必ずしもまっすぐではありません。円弧状のチャネルもあります。この場合、LRはうまく機能しません。
そこで、多項式回帰が活躍する。
PRグラフはチャンネルの中心をまっすぐ進み、その最終ポイントもチャンネルの中心になります。
ここで、もうひとつのアーク。(つまり正弦波のスライス)。
デメリットも考えないと...。
しかし、基本は同じで、カーネル変換を使って新しい次元にマッピングを導入することで依存関係を再構築し、その上にさらに別のものを追加しているのです
この方がもっといい。
それを解決する方法を考える。
Maxim Dmitrievsky:
予測についてはどうでしょうか?))
欠陥?)
それを解決する方法を考える。
を今の次元で解決することはできない、それが問題なのです。あなたの回帰は、そのような事象が発生する可能性について何も知りません
ちなみに、ビクターはカーネル確率密度について、こちらの記事を掲載しています。
カーネルのトリックではなく、特徴ベクトルを他の空間にマッピングすることだと思うのですが
少なくとも私見では...未読です。
を今の次元で解決することはできない、それが問題なのです。あなたの回帰は、そのような事象が発生する可能性について何も知りません
欠点?)
こんな感じです。
それを解決する方法を考える。
通常はこのようなものです。
を今の次元で解決することはできない、それが問題なのです。あなたの回帰は、そのような事象が発生する可能性について何も知りません