Boxplotによる金融時系列のシーズンパターンの探索

効率的な相場仮説を反証し、相場サイクルの存在を証明しようとする試み

2013年、効率的な相場仮説を立てたユージン・ファマ(Eugene Fama)はノーベル経済学賞を受賞しました。 彼の仮説によると、資産価格はすべての実質的な情報を完全に反映します。 これは相場参加者は全員平等であることを意味します。 

ただし、仮説自体には含みがありますが、この効率性は次の 3 点があります。

• 相場資産価格がこの資産に関する過去の情報を完全に反映している場合、弱い
• 価格が過去だけでなく、現在の公開情報を反映する場合、平均
• さらに非公開のインサイダー情報を反映するとき、強い

効率の程度に応じて、相場は予測可能性の度合いが異なります。 テクニカルアナリストにとって、これは、相場に異なる周期的なシーズン成分が存在する可能性があることを意味します。

たとえば、相場の活動は年ごとに、月から月、セッション、時間から時間などによって異なる場合があります。 さらに、この種のサイクルは、トレーダーがアルファを見つけることができる予測可能なシーケンスと表すことができます。 サイクルはまた、さらに探求できる異なる組成パターンで重なり、作成することができます。 

価格増分でシーズンパターンを検索

複合サイクルと一緒に定期的なサイクルを研究することができます。 金融商品の月次変動を研究する例を見てみましょう。 このため、IPython言語とMetaTrader5ターミナルの組み合わせを使用します。

ターミナルから直接クオートをインポートできるようにするには、次のコードを使用します。

from MetaTrader5 import *
from datetime import datetime
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt 
%matplotlib inline
import seaborn; seaborn.set()
# Initializing MetaTrader5 connection 
MetaTrader5Initialize("C:\\Program Files\\MetaTrader5\\terminal64.exe")
MetaTrader5WaitForTerminal()

print(MetaTrader5TerminalInfo())
print(MetaTrader5Version())

ターミナルへのパスを指定します。

分析を開始するには、さらに数行を追加します。

rates = pd.DataFrame(MetaTrader5CopyRatesRange("EURUSD", MetaTrader5_TIMEFRAME_D1, datetime(2010, 1, 1), datetime(2020, 1, 1)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)

# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
returns.head(5)

Monthly_Returns = returns.groupby([returns.index.year.rename('year'), returns.index.month.rename('month')]).mean()
Monthly_Returns.boxplot(column='close', by='month', figsize=(15, 8))

rates変数は、指定された時間間隔 (この例では 10 年) の価格で pandas データフレームを受け取ります。 今回は終値(さらなる解釈を簡素化するために)にのみ関心があるとします。 rates.drop() メソッドを使用して不要なデータ列を削除してみましょう。

価格は、時間とフォームのトレンドの平均値のシフトがあるので、統計分析はそのような生の系列には適用されません。 価格の変化率(価格の増分)は、通常、すべて同じ値の範囲にあることを確認するために計量経済学で使用します。 変更の割合は pd.DataFrame(rates['close'].pct_change(1)) メソッドを使用して受け取ることができます。

平均月額価格帯が必要です。 月単位の平均値を年単位で受け取るようにテーブルを配置し、Boxplotに表示します。

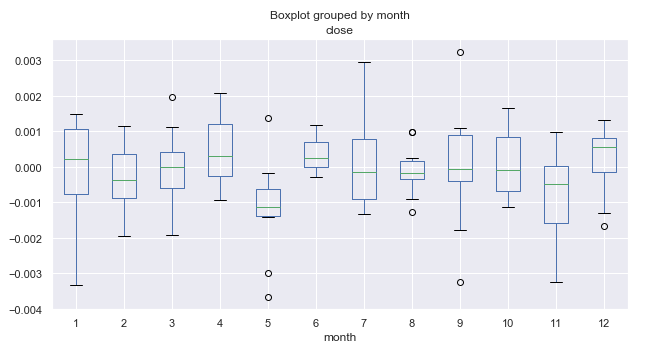
図1. 10 年間の月別の平均価格増分の範囲。

Boxplotとは何か、どのように解釈するべきでしょうか。

選択した期間の価格データのボラティリティまたは分布に関するデータにアクセスする必要があります。 各Boxplot(あるいは"ボックスアンドウイスキーダイアグラム") は、データセットに沿って値がどのように分布しているかを示す優れたものです。 Boxplotは、視覚的に似ていますが、ローソク足チャートと混同しないでください。 ローソク足とは異なり、Boxplotは5つの読み取りに基づいてデータの分布を表示する標準化された方法を提供します。

1. 中央値、Q2、または50パーセンタイルは、データセットの平均値を示します。 この値は、図のボックス内に緑色の水平線で表示されます。
2. ファーストクオンタイル Q1 (または 25 パーセンタイル) は、Q2 とサンプル内の最小値の間の中央値を表し、 99% 信頼区間に収まります。 図のボックス "body" の下端として表示されます。
3. サードクオンタイルQ3(または75パーセンタイル)は、ボックスの上端"body"として示されるQ2と最大値の間の中央値です。
4. 箱の本体は、IQRとも呼ばれるインタークオンタイルレンジ(25番目と75番目の百分位数の間)を形成します。
5. 箱ひげはディストリビューションを補足します。 サンプル分散全体の 99% を扱い、上下のドットは 99% の値範囲を超える値を示します。

このデータは、変動の範囲と内部範囲内の値の分散を評価するのに十分です。

シーズンパターンのさらなる分析

図1を詳しく考えてみましょう。 5 番目の月 (5 月) の増分の中央値が 0 に対して相対的にシフトし、0 を超える外れ値が表示されることがわかります。 一般的に、10年間の統計からわかるように、5月の相場は3月に比べて減少していました。 5月に相場が成長した年は1年しかありませんでした。 これは興味深い考案です。トレーダーの格言にうまく準拠しています。"5月は売って、撤退！"。

5月に続く6ヶ月目(6月)を見てみましょう。 ほぼ常に(1年を除いて)相場は5月に対して6月に成長していた。繰り返されるパターンであることを示します。 6月の変動の範囲は小さく、外れ値(5月とは異なり)がなく、シーズン的な安定性が良好であることを示します。

11月(11月)に注意を払ってください。 この期間中に相場が下落する確率は高いです。 その後、12月には、相場は通常再び上昇しました。 1月(第1月)は、高値のボラティリティと12月に対する下落によってマークされました。

取得したデータは、トレード決定を行うための基礎となる条件の有用な概要を提供することができます。 また、確率はトレードシステムに統合することができます。 たとえば、特定の月に複数の買いや売りを行うことができます。

月次サイクルデータは興味深いものですが、より短い日のサイクルをさらに深く見ることは可能です。

同じ 10 年間の期間を使用して、各曜日の価格増分の分布を表示してみましょう。

Daily_Returns = returns.groupby([returns.index.week.rename('week'), returns.index.dayofweek.rename('day')]).mean()

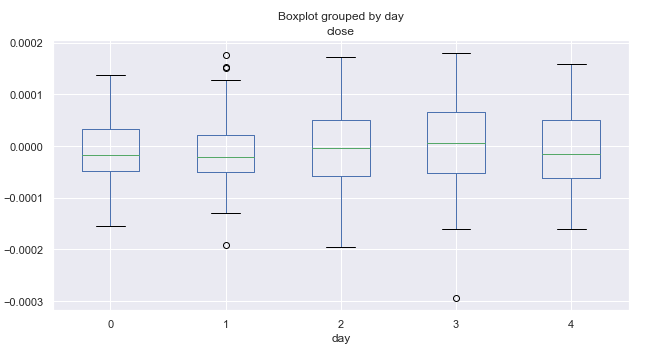
図2. 平均価格増分、10年以上のトレード日別の範囲。

ここでは、0 は月曜日に、4 から金曜日に対応します。 価格帯にのっとると、日によってボラティリティはほぼ一定のままです。 トレードは週の特定の日に、より集中的であると結論付けることはできません。 平均して、相場は月曜日と金曜日よりも下がる傾向があります。 おそらく、別々の月に、日ごとの分布は異なる様相があります。 追加の分析を実行してみましょう。

# leave only one month "returns.index[~returns.index.month.isin([1])"
returns = returns.drop(returns.index[~returns.index.month.isin([1])])

上記のコードでは、1 月に 1 を使用します。 この値を変更することで、10 年間の任意の月の統計を取得できます。

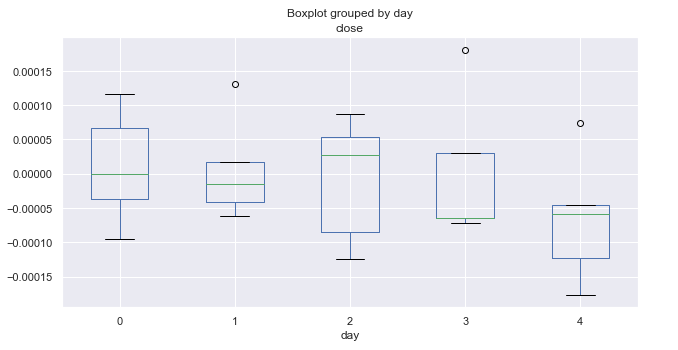
図3. 平均価格の増分、10年間(1月)のトレード日数別の範囲。

上の図は、1 月の日単位での増分の分布を示します。 この図では、すべての月の要約統計と比較してより有用な詳細が提供されるようになりました。 金曜日には相場が減少するトレンドがあることをはっきりと示します。 EURUSDペアが下がらなかったのは一度だけです(ゼロより上の外れ値で示されています)。

3月の同様の統計を次に示します。

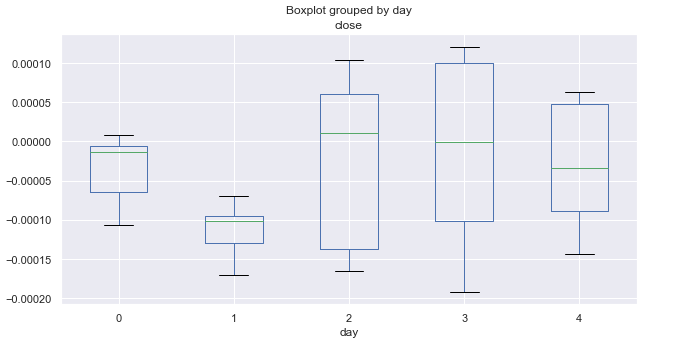
 図4. 平均価格の増分、10年以上のトレード日(3月)の範囲。

3月の統計は1月とは全く異なります。 月曜日と火曜日(特に火曜日)は弱気のトレンドを示します。 すべての火曜日は大幅な減少で閉じましたが、残りの日数はゼロ前後で変動します(平均)。 

10月を見てみましょう:

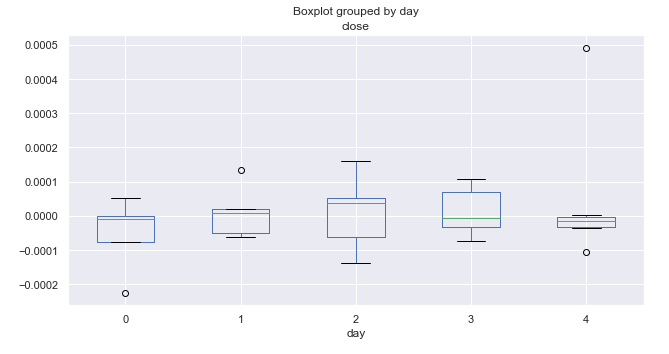
図5. 平均価格の増分、10年間(10月)のトレード日別の範囲。

曜日による増分分布の分析では、目立つパターンは明らかにされませんでした。 価格の動きの最高の範囲と可能性がある水曜日に選び出すことができます。 他のすべての日は、上向きと下向きの動きの確率が等しく、外れがあります。

シーズンの日中パターンの分析

多くの場合、トレードシステムを作成する際に日中の分布を考慮する必要があります, 例えば、日ごと、毎月の分布に加えて、時間単位のデータを使用します。 これはかんたんに行うことができます。

各時間の価格増分の分布を考慮してください。

rates = pd.DataFrame(MetaTrader5CopyRatesRange("EURUSD", MetaTrader5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)

# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]

Hourly_Returns = returns.groupby([returns.index.day.rename('day'), returns.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(10, 5))

10年間の15分の時間枠のクオートです。 もう 1 つの差は、データが日と時間でグループ化され、サブサンプルのすべての日の中央値の時間統計を取得することです。

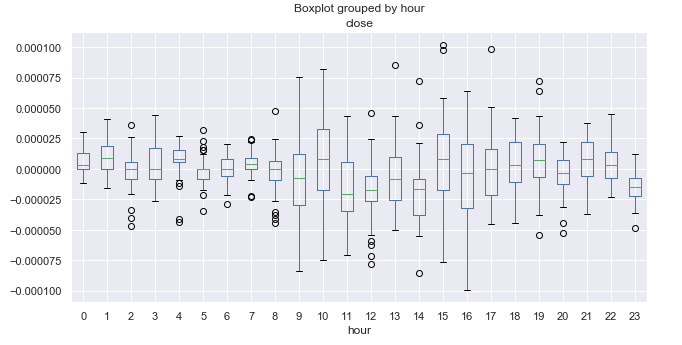
図6. 10 年以上の平均価格増分の範囲（時間単位）

ここでは、ターミナルの時間帯を知る必要があります。 今回の場合は+2です。 参考までに、メインFOREXトレードセッションの開始時間と決済時間をUTC+2で書いてみましょう。

Session	Open	Close
Pacific	21.00	08.00
Asian	01.00	11.00
European	08.00	18.00
American	14.00	00.00

太平洋セッション中のトレードは通常静かです。 箱のサイズを見ると、静かなトレードに対応する21.00-08.00の範囲が最小限であることに気づきます。 この範囲は、ヨーロッパとアメリカのセッションの開始後に増加し、その後、徐々に減少し始めます。 日の時間枠で明白な周期的なパターンはないようです。 平均増分は、上向きまたは下向きの明確な時間を除いて、ゼロの周りに変動します。

興味深い期間は23.00(アメリカのセッションの終わり)で、その間の価格は通常22.00に対して減少します。 トレードセッションの終了時に修正を示す場合があります。 00.00で価格は23.00に対して相対的に成長するので、規則性として扱うことができます。 より顕著なサイクルを検出することは困難ですが、価格帯の全体像を把握し、現時点で何を期待すべきか分かります。

単一のラグでインクリメントのトレンドを解除すると、パターンを隠すことができます。 したがって、任意の期間を持つ移動平均によってトレンドが下がったとデータを見るのは妥当です。

MAによってトレンドが下ったシーズンパターンを検索する

トレンド成分の適切な決定は難しいです。 時には時系列があまりにも滑らかにすることができます。 この場合、トレードシグナルはほとんどありません。 平滑化期間が短縮された場合、トレードの高値頻度はスプレッドと手数料をカバーできない可能性があります。 移動平均を使用してトレンドを削除するようにコードを編集してみましょう。

rates = pd.DataFrame(MetaTrader5CopyRatesRange("EURUSD", MetaTrader5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
rates = rates.set_index('time')
# set the moving average period
window = 25
# detrend tome series by MA
ratesM = rates.rolling(window).mean()
ratesD = rates[window:] - ratesM[window:]

plt.figure(figsize=(10, 5))
plt.plot(rates)
plt.plot(ratesM)

移動平均期間は 25 に設定されます。 このパラメータと、終値がリクエストされる期間は変更できます。 15分の時間枠を使用します。 その結果、1時間ごとに15分の移動平均から終値の平均偏差が得られます。 結果の時系列は次のとおりです。

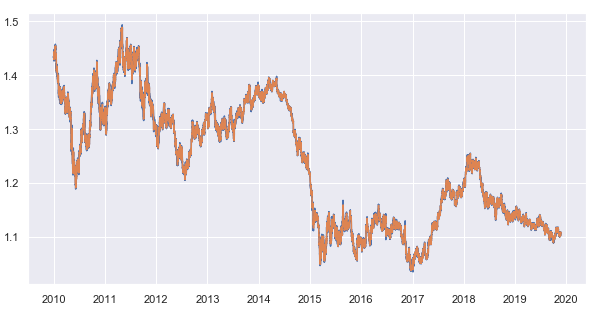
図7. 15分時間枠の終値と25期間の移動平均

終値から移動平均を引いて、トレンドの解除された時系列(残り)を取得します。

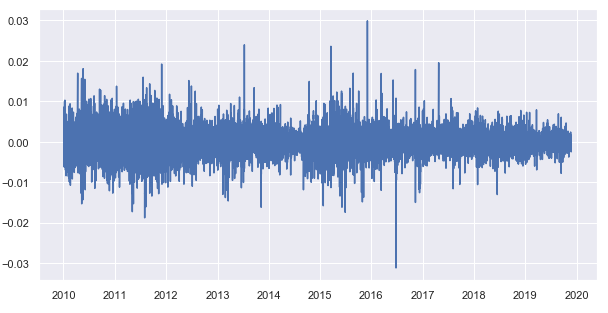
図8. 終値からの移動平均の減算からの余り

では、各トレード時間の剰余の分布の時間ごとの統計を取得してみましょう。

Hourly_Returns = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(15, 8))

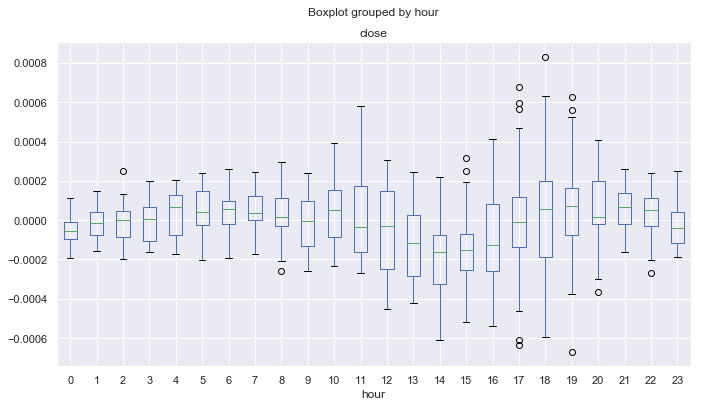
図9. 平均価格増分の範囲は、時間単位で、10年以上にわたり、25期間のMAによって減少

図6 の図は、単一のラグで価格の増分に作成された図とは異なり、外れ値が少なく、より周期的なパターンを示します。 たとえば、通常、0.00 から 08.00 (太平洋セッション) の価格は移動平均に対して順調に上昇していることがわかります。 下降トレンドは12.00から14.00まで定義できます。 その後、米国のセッション中に、価格は平均で上昇します。 太平洋セッションの開始後、価格は21.00から4時間下落します。

次の論理的なステップは、より正確な統計的推定値を得るために分布モーメントを精査することです。 たとえば、結果として得られたトレンド解除系列の標準偏差をBoxplotとして計算します。

Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).std()

                                                                                       

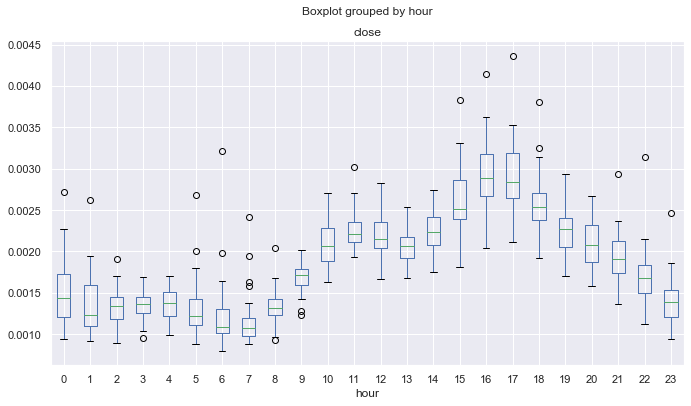
図10. 価格の平均標準偏差は、時間単位で、10年以上にわたり、25期間MAによってトレンドが低下。

図10は、数学の期待値からの標準偏差の点で最も安定した価格挙動を有する時間を示します。 たとえば、時間 4、13、14、19 は、すべての日に安定した分散を持っており、平均反転戦略にとって魅力的だとみることができます。 他の時間は外れ値と長い口ひげがある可能性があり、異なる日でより変動するボラティリティがあることを示します。

もう一つの興味深い点は非対称係数です。 計算してみましょう:

Hourly_skew = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).skew()

 

図11. 価格の平均非対称係数は、時間単位で、10年以上にわたり、25期間MAによってトレンドが低下

0 と小さな分散に近い場合は、増分の "標準" 分布が多いことを示します。 図の形は凹状になります。 例えば、欧米のセッションの変動は分散が大きくなっていますが(図9)、太平洋やアジアのセッションとは異なり、時間単位の分布はより安定しており、偏りが少なくなります。 トレード活動が突然の動きに置き換えられ、分配バイアスに大きく寄与する直近の2つのセッションの間の活動の大きな変動に起因する可能性があります。

過剰な統計も、同様の結果を示しています:

Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).apply(pd.DataFrame.kurt)

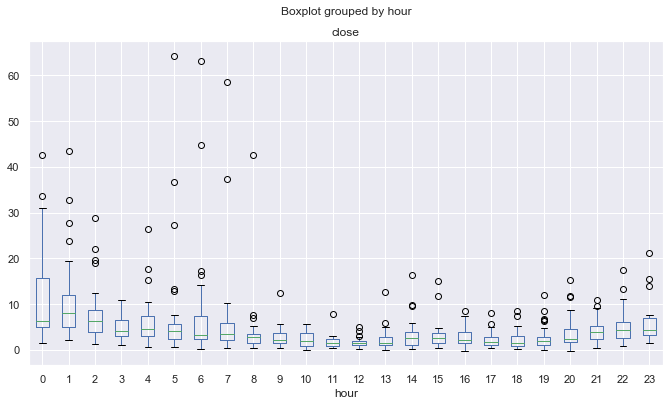
図12. 平均超過価格の係数は、25期間MAによって10年以上、時間単位で増加

前述の可能な効果に、ディストリビューションは天井に達しなくなり、よりボラティリティの高いトレードセッションの場合はより多くの "regular" が発生しますが、静かなトレードセッションでは "イレギュラー" になります。 これは一種のパラドックスです。

特定の月または曜日の MA によってトレンドを取り下げたシーズンパターンを検索する

各月のトレンドの下降した時間単位の価格分布と、曜日ごとに個別に表示できます。 コード全体は、以下の添付ファイルで使用できます。 ここでは、3月と11月の比較のみを行います。

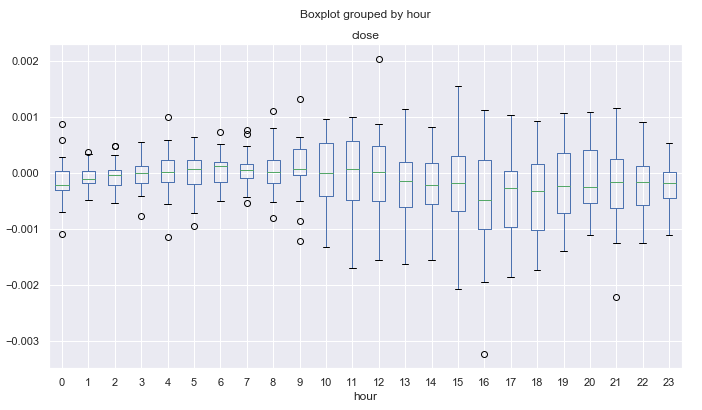
図13. 平均価格増分は、3月の25期間MAによって減少した10年以上の時間単位で範囲

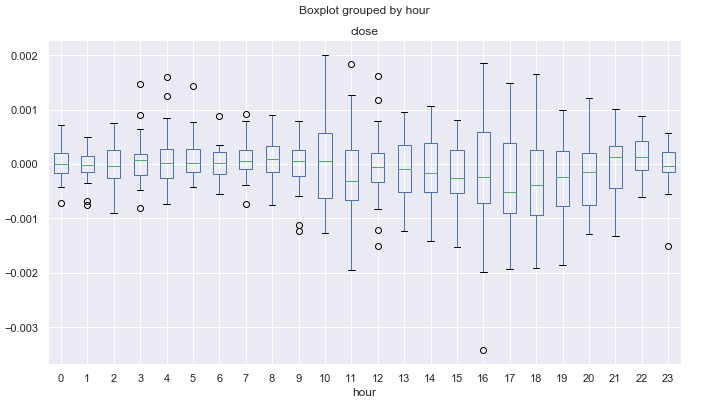
図14. 平均価格増分は、11月の25期間MAによって減少した10年以上の時間単位で範囲

ティックデータを含む日中サイクルの小さい方を検索することは可能ですが、ここではトレーダーの意見に従って、金融時系列に存在する可能性のある基本的なシーズンパターンのみを扱います。 このデータは、金融商品のシーズン的な特徴を考慮して、独自のトレードシステムを開発するために使用することができます。  

トレーディングロジックを使用したパターンのチェック

図9に示されている見つかったパターンを利用する、簡単なトレーディングEAを作成しましょう。 0.00から04.00(GMT +2)まで、EURUSDの価格は4時間の平均に対して上昇することを示します。

//+------------------------------------------------------------------+
//|                                              Seasonal trader.mq5 |
//|                                  Copyright 2020, Max Dmitrievsky |
//|                        https://www.mql5.com/ja/users/dmitrievsky |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, Max Dmitrievsky"
#property link      "https://www.mql5.com/ja/users/dmitrievsky"
#property version   "1.00"

#include <MetaTrader4Orders.mqh>
#include <Trade\AccountInfo.mqh>
#include <Math\Stat\Math.mqh>

input int OrderMagic = 666;
input double   MaximumRisk=0.01;
input double   CustomLot=0;

int hnd = iMA(NULL, 0, 25, 0, MODE_SMA, PRICE_CLOSE);
MqlDateTime hours;
double maArr[], prArr[];

void OnTick()
  {
//---
      CopyBuffer(hnd, 0, 0, 1, maArr);
      CopyClose(NULL, 0, 0, 1, prArr);
      double pr = prArr[0] - maArr[0];
      
      TimeToStruct(TimeCurrent(), hours);
      if(hours.hour >=0 && hours.hour <=4)
         if(countOrders(0)==0 && countOrders(1)==0)
            if(pr < -0.0002) OrderSend(Symbol(),OP_BUY,0.01,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN);
            
      if(countOrders(0)!=0 && pr >=0)
         for(int b=OrdersTotal()-1; b>=0; b--)
            if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) {
               if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
            }
         
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int countOrders(int a) {
   int result=0;
   for(int k=0; k<OrdersTotal(); k++) {
      if(OrderSelect(k,SELECT_BY_POS,MODE_TRADES)==true)
         if(OrderType()==a && OrderMagicNumber()==OrderMagic && OrderSymbol() == _Symbol) result++;
   }
   return(result);
}

使用する移動平均は、統計推定値と同じです。 25の期間を有します。 直近の既知の価格から平均値を引いて、現在のトレード時間が 0:00 から 4:00 の範囲にあるかどうかを確認します。 図9からわかるように、この期間の終値と移動平均の最大差は-0.0002に等しく、MAはゼロを上回っています。 したがって、トレードロジックは、この差に達したときに買いトレードを開き、ゼロに達したときにポジションを閉じるようにすることです。 テストロボットにはストップオーダーやその他のチェックはありません。 15分の時間枠(MAは研究でこの期間に基づいて構築された)、すべてのティックモードで2015年から2019年までのテストを実行します。

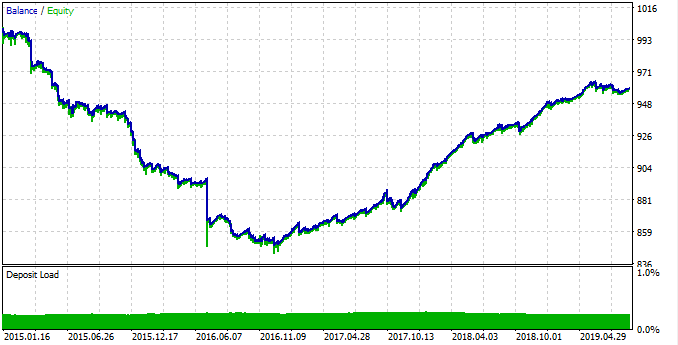
図15. 見つかったパターンのテスト。

このパターンは2015年から2017年までうまくいきませんでしたが、チャートは下がっていました。 その後、2017年から2019年にかけて安定した成長が見られました。 なぜこのようなことが起こったのでしょうか。 これを理解するために、各時間間隔の統計を個別に表示しましょう。

まず、収益性の高いトレード間隔を次に示します。

rates = pd.DataFrame(MetaTrader5CopyRatesRange("EURUSD", MetaTrader5_TIMEFRAME_M15, datetime(2017, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])

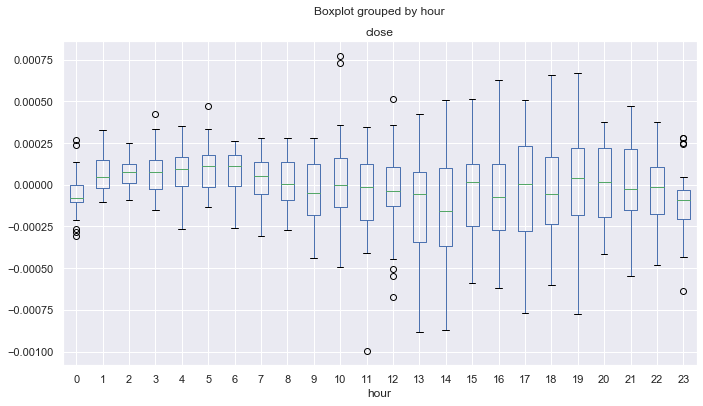
図16. 2017-2019年の統計。

見てわかるように、すべての時間の中央値(ゼロを除く)は、移動平均に対してゼロを超えています。 統計的にアルファは、トレードシステム側にあり、システムは、平均で利益のままです。 さて、ここに2015-2017の分布があります。

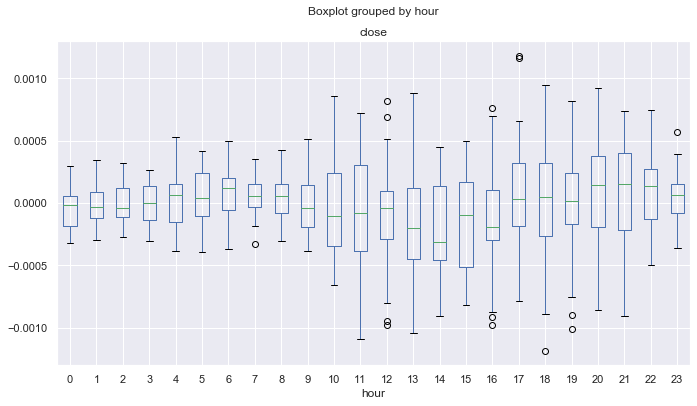
図17. 2015-2017年の統計。

ここでは、分布の中央値は、4番目を除くすべての時間のnull以下であり、利益を得る確率が小さいという意味です。 さらに、ボックスの平均範囲は、最小値が -0.00025 より小さくない別の時間間隔と比較して大幅に大きくなります。 ここではほぼ-0.0005です。 もう一つの欠点は、終値でのみ分布のクオートであり、したがって価格の急騰は考慮されません。 この記事の範囲外であるティックデータを分析することで修正できます。 差は明らかですので、すべての年の結果を均一にするためにシステムを微調整しようとすることができます。

0-1時間のみトレードを開始できるようにしましょう。 したがって、平均偏差は正の方向に移動するトレンドがあるため、今後数時間でトレードはプラスで決済されると仮定します。 また、トレード決済の閾値を 0.0 から 0.0003 に増やすと、ロボットはより多くの潜在的な利益を取ることができます。 変更は以下のコードに示されています。

TimeToStruct(TimeCurrent(), hours);
      if(hours.hour >=0 && hours.hour <=1)
         if(countOrders(0)==0 && countOrders(1)==0)
            if(pr < -0.0004) OrderSend(Symbol(),OP_BUY,LotsOptimized(), SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN);
            
      if(countOrders(0)!=0 && pr >= 0.0003)
         for(int b=OrdersTotal()-1; b>=0; b--)
            if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) {
               if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
            }

最終的な結論を導くためにロボットをテストしてみましょう:

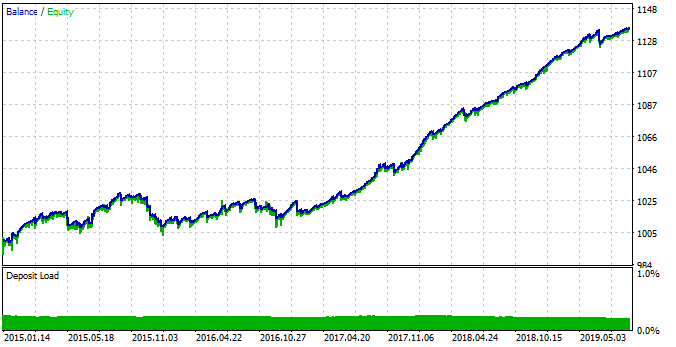
図18. EAパラメータを変更して検出されたパターンをテスト。

も他の人よりも優位性を持たいこ今回は、2015年から2017年の間の時間間隔でシステムがより安定します。 しかし、シーズンパターンの変化により、この期間は2017年から2019年の間ほど効率的ではありませんでした。 この動作は、Boxplotを使用して記述できる相場の根本的な変化に関連します。

もちろん未知のパターンはたくさんありますが、この基本的な例は、そのような手法を使うときに新しい可能性を提供します。

結論

この記事では、財務時系列のシーズンパターンを検出するための提案された統計手法について説明しました。 相場は、月に応じて、月のシーズンサイクルだけでなく、日中に周期性が発生することがあります。 時間単位の分析では、あるスムージング期間(移動平均など)では、セッション内とトレードセッション間の移動時の両方で特定のサイクルを見つけることができることが示されています。

このアプローチの利点の1つは、特定の相場パターンで動作する可能性と、過剰最適化(オーバーフィット)が存在しないため、トレードシステムは安定します。

この欠点については、シーズンパターンマイニングプロセスは容易ではなく、さまざまな組み合わせやサイクル操作を伴います。

この分析は EURUSD 通貨ペアに対して実行され、10 年の期間が設定されました。 Python のソースコードは、記事のトレーリングストップに .ipynb 形式 (Jupyter ノートブック) で添付されています。 任意の金融商品に対して、添付ライブラリを使用して同じ調査を行い、取得した結果を適用して独自のトレードシステムを作成したり、既存のトレードシステムを改善することができます。