
適応型相場の実用的評価法
イントロダクション
この記事のトレード戦略は、最初にVladimir Kravchukが 雑誌"Vladimir Kravchuk" 2001-2002 で説明しています。 このシステムは、ディジタルフィルタの使用と離散時系列のスペクトル推定に基づいています。
クオートの変更のライブチャートは、任意の形式を持つことができます。 数学では、このような関数はnon-analyticと呼ばれます。 有名なフーリエ定理は、有限時間間隔の任意の関数が正弦関数の無限の和として表現できることを意味します。 したがって、周波数スペクトルと呼ばれる周波数関数によって、任意の時間信号を一意に表すことができます。
非ランダム信号については、時間領域から周波数領域表現への遷移 (すなわち、周波数スペクトルの計算) はフーリエ変換を用いて行われます。 ランダムプロセスは、プロセスのパワースペクトル密度 (PSD) によって表されますが、ランダムプロセス自体ではなく、その自己相関関数のフーリエ変換です。
1. 戦略の理論的側面
フィルタリングは、信号の周波数スペクトルを正しい方向に変更することを忘れないでください。 このような変換は、特定の範囲内の周波数成分を増幅または弱めることができます。 ディジタルフィルタは、離散時間でのみ定義された信号を変換するためのディジタルシステムです。
デジタルフィルタと離散時間系列を使用する場合、重要な側面があります。
まず、最も人気のある技術ツール (MA、RSI 、モメンタム、ストキャスティクスなど) は、信号の周波数スペクトルの変化に基づいており、したがって、デジタルフィルタです。 伝達関数の利得は周波数によって異なります。 しかし、この伝達関数は多くの場合、無視されます。 したがって、ほとんどのユーザーは、信号の周波数スペクトルが変動する方向を知らず、したがって、シグナルに対するインジケータの影響の本質を理解していません。 インジケーターの調整とその値の解釈が複雑になります。
第2に、通貨のクオートの動きのプロセスは、常に離散信号のように、一般的なプロパティを考慮するときにテクニカルインジケーターを開発する必要があります。 したがって、例えば、離散信号のスペクトルは常に周期関数です。 このプロパティを無視すると、インプットタイムシリーズの回復不能な歪みが発生する可能性があります。
第3に、価格変動のスペクトル密度は、相場によって大きく異なります。 このような場合、ユーザーはインジケーターパラメータを構成するための個別のアルゴリズムを持っていません。代わりに、任意のパラメータを選択し、実際の一貫性をテストする必要があります。
多くの場合、事前に最適化されたインジケーターやEAは、昨日もよく働いていたとしても、今日悪い結果与えるかもしれません。 これは、時系列の非定常性によるものです。 実際には、1つの相場の2つのタイムフレームで計算された2つの PSD の推定値を比較すると、スペクトルの天井の振幅がシフトし、そのフォームを変更します。 レシーバに対して高調波のソースを移動すると、波長を変更するドップラー効果の表れとして解釈することができます。 相場のトレンドの動きを再度証明します。
適応性がある相場の次の目的は、最低のリスクで最高の収益性のあるトレードのアルゴリズムを作成することです。 これは段階的に実現されます。
- 特定の相場の価格変動のスペクトルの構成を検討します。
- 非再帰的なデジタルフィルタは、アダプティブに構成されます。 このプロシージャは、最適化されたインパルス応答 (インパルス応答関数、IRF) のセットを結果とします。
- インプット時間系列は、フィルタリングされ、最終的に一連のインジケーターが決定され、この記事でさらに検討します。
- このトレーディングアルゴリズムが開発されています。
1.1. スペクトル分析法の選択
適応相場に基づくトレーディングシステムの開発は、特定のインストゥルメントの価格移動スペクトルの研究から始まります。 明らかに、システム全体の最終的な有効性は、この段階に依存します。
このソリューションは、明らかです。つまり、 スペクトルまたは高調波解析を実行する必要があります。 しかし、どのメソッドを選択しましょう? 今日では、スペクトル解析手法の2つの主要なクラスが知られています: パラメトリックとノンパラメトリック。
スペクトル解析のパラメトリック法は、特定のスペクトル密度モデルが定義され、そのパラメータが限られた時間間隔で対応するプロセスの観測結果に基づいて推定されるメソッドです。 元のモデルは様々な形を持つことができます。
特に、有理関数として表される時系列のスペクトル密度は、ソースモデルとして機能することができます。 この場合、自己回帰モデル、移動平均モデル、および自己回帰移動平均モデルを実装することができます。 したがって、モデルパラメータを推定する際には、さまざまなメソドジカルアプローチが使用されます。
この問題を解決するために、また、変分原理と品質評価の対応する関数を使用することができます。 ここでは、ラグランジュ乗数は推定パラメータとして機能します。 このアプローチは、相関関数の既知の別個の値に従ってプロセスのエントロピーを最大化する必要がある極大エントロピー法によるスペクトル密度の推定に適用されます。
スペクトル解析のノンパラメトリック法パラメトリックのものとは異なり、任意のモデルを持っていません。 その中で最も人気のあるのは、初期段階でプロセスの周期性が決定されるメソッド です。(すなわち、既存の実装のフーリエ変換の絶対値の2乗) この後、このタスクは、特定の要件を満たす適切なウィンドウを選択するために削減されます。
Blackman–Tukey法も広く使用されています。 解析された時系列の相関系列の重み付け推定のフーリエ変換です。
もう1つのアプローチは、時系列のスペクトル密度を推定し、直交増分を持つランダムなプロセスを通して解析された時系列のフーリエ変換を記述する、基本的な積分方程式を解くという問題を減らすことにあります。
提案されたトレーディングシステムの著者によると、スペクトル推定の古典的なノンパラメトリック法を用いて、為替レート変動のパワースペクトル密度を定性的に評価することは不可能です。 唯一の方法は、プロセスが静止しているか、線形のトレンドを除去することによってそうすることができる、比較的短い離散時間のサンプルの PSD の一貫性のある推定値を取得し、スペクトル解析のパラメトリックメソッドを使用することです。 スペクトル推定の様々なパラメトリック法の中で最大エントロピー法は最も注目に値します。
1.2. 応用テクニカル分析ツール
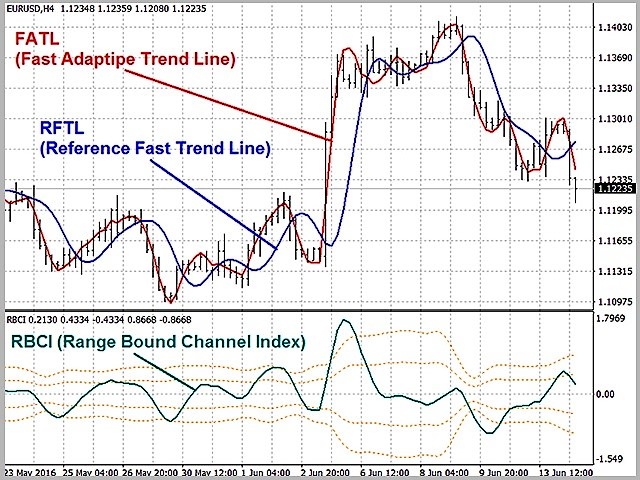
提示された戦略の主な差は、アダプティブトレンドラインです。 その方向は、現在のトレンドの方向を示します。
アダプティブトレンドラインは、インプット時間系列の低周波成分です。 これはローパスフィルタ (LPF) によって得られます。 LPF のカットオフ周波数fc を低くすると、トレンドラインのスムージングが大きくなります。
アダプティブトレンドラインのポイント間には内部接続があり、間の距離に反比例する強さがあります。 接続は、TN = 1/(2 fc) のいわゆるナイキスト間隔と同等以上の距離を持つポイント値の間でのみ存在します。 その結果、フィルタのカットオフ周波数の低下は、この接続を強化し、トレンド反転の瞬間が延期されます。
このトレーディングシステムは、トレンドを識別するために異なるタイムフレームを持つ2つのアダプティブトレンドラインを使用しています。
FATL (高速アダプティブトレンドライン)。 プロットにはLPF-1 フィルタが必要です。 非常に短い周期で、高周波ノイズや相場サイクルを抑制します。
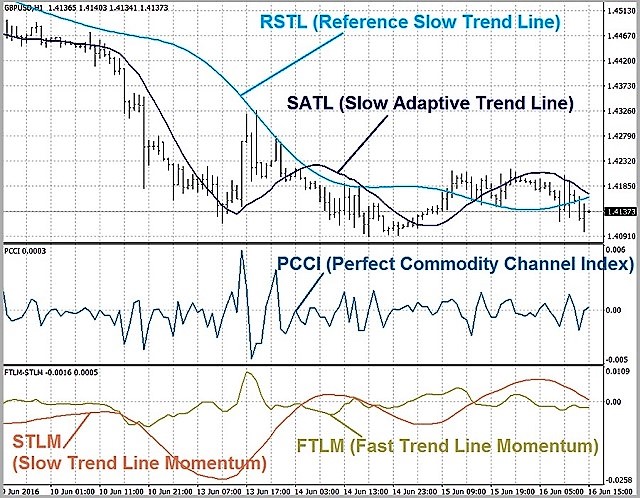
SATL (低速アダプティブトレンドライン)。 プロットには LPF-2 フィルタが必要です。 LPF とは異なり、より長い周期で相場を循環させることができます。
上記のフィルタのパラメータ (遮断周波数fc と停止帯域の減衰σ) は、解析されたスペクトルの推定値に基づいて計算します。 LPF-1 および LPF-2 は、少なくとも40dB のストップ帯域での減衰を提供します。 通過域のインプット信号の振幅と位相に影響を与えません。 デジタルフィルタのこのプロパティは、効果的なノイズ抑制を提供し、 MAs に比べてダマシシグナルが減ります。
数学的な観点から見ると、FATL (k) の値は、k がトレード日の数である Close (k) の期待値です。
RFTL (リファレンスファストトレンドライン)とRSTL (リファレンススロートレンドライン)。 ディジタルフィルタ LPF-1 および LPF-2 によって出力されるインプットシグナルに応答して、対応するナイキストインターバルと同じ遅延を表します。
FTLM (ファストトレンドラインモメンタム)およびSTLM (スロートレンドラインモメンタム)は FATL および SATL のシフトを示します。 モメンタムと同様に計算されるが、近い価格の代りにフィルターによって滑らかにされたトレンドラインを使用します。 結果として得られるラインは、従来のモメンタムよりも滑らかです。
FTLM と STLM ラインは離散数学のルールに従って計算されます。 プロセスのバンドに限られている2つの隣接する独立したポイントの差です。 この要件は、多くの場合、モメンタムの通常の計算で無視され、その結果、回復不可能な歪みは、インプットシグナルのスペクトルに表示されます。
RBCI (Range Bound Channel Index). 次のようなバンドパスフィルタによって計算されます。
- 低周波スペクトル成分から、T2 = 1/fc2より大きい周期を持つ低周波トレンドを削除します。
- 高周波スペクトル成分から構成される高周波ノイズを、T1 = 1/fc1未満の期間で削除します。
条件Т2 > T1が満たされるように、ピリオドТ1とТ2が選択されます。 同時に、 fc1とfc2のカットオフ周波数は、すべての支配的な相場サイクルを考慮する必要があります。
単純に言えば、RBCI (k) = FATL (k)-SATL (k) です。 実際、RBCI がローカルの極値に近づくと、価格はトレード範囲の上下の境界に近づきます。(それぞれが高いか低いかによって異なります)
PCCI (Perfect Commodity Channel Index). 計算式: PCCI (k) = close(k)-FATL (k)。
その計算メソッドは、商品チャネルインデックス (CCI) と似ています。 確かに、CCI は、現在の価格とその移動平均の間の正規化された差であり、PCCI は、毎日の終値とその期待される値 (前述のように FATL の値から取られた) の差です。
つまり、PCCI インデックスは、標準偏差に正規化された価格変動の高周波成分です。
1.3. インジケーターシグナルの解釈のルール。
トレーディングシステムの主な原則を示すことができます。
- トレンドに沿ってトレードと、トレンドベースのシステムに属しています。 このトレンドは、SATL を使用して識別されます。
- エントリポイントは、FTLM と STLM の "高速" と "低速" のトレンドの動的特性に応じて決定されます。
- この計算は RBCI によって現在の相場の状態 (中立、買われ過ぎ、売られ過ぎ、ローカル極値) を使用します。
- 相場参入方向は、トレンドインジケーターを使用して決定されます。 オシレーターはレンジの場合にのみ使用できます。
- ストップオーダーを設定することは必須です。(RBCI、PCCI 指数、相場のボラティリティ)
上記のツールは、ルールに従って解釈する必要があります。
- SATL ラインが上向きに指示されれば、上昇トレンドが相場に存在しています。 局所的な極値の出現はトレンドが逆転し始めたことを示す。 RSTL とのクロスは、トレンドが完全に逆転したというサインです。 この場合、STML はその符号を変更します。
- SATL 線が水平またはほぼ水平である場合、レンジが相場に存在します。
- STLM は強気のトレンドにポジティブで、弱気のトレンドに否定的です。 これはメインインジケーターと見なされます。 その局所的な極端は、常に対応する SATL 両極端の外観の前に。 STLM の絶対値は、トレンドの強さに正比例します。 STLM と SATL が同じ方向に動くと、そのトレンドは力強さを増しています。 異なった方向はトレンドの弱まることを示します。 水平 STLM 線は、完全に形成されたトレンドを意味します。
- 「高速」と「低速」のトレンド線 (FATL と SATL) が同じ方向にある場合、そのトレンドの強さは大きくなります。 そうでない場合、相場は統合されるか、または訂正段階にあります。
- FATL と SATL 線が同じ方向に移動し始めた場合、トレンドは反転しています。 方向が multidirectionality の期間の後で再度収束すれば、相場の変化は終わり、価格は再度 SATL の方向の移動を始めます。
上記のルールから主要なトレードシグナルを定式化してみましょう。
- 信頼性の高い反転シグナルは、長期的なトレンドの冒頭に表示されます。 シグナルの形成の間に、価格のボラティリティが急激に増加します。 トレンドの変化の兆候です。 したがって、PCCI は、トレードを開くためのポイントを選択するときに考慮する必要があります。 弱気のシグナルでは、PCCI オシレーターは、最後のロウソクが閉じたときに-100 レベルの上にある場合、売りです。 PCCI 値が-100 を下回る場合は、トレードを開かないで、オシレーターがこのレベルを超えるのを待ちます。
- 次のシグナルは短い修正の後で形作られ、増強されたトレンドの継続を示します。 原則として、このような状況でのボラティリティは、トレンドの反転時よりも低くなっています。 そのため、ここではシグナル生成条件が厳しく、シグナル自体がより信頼性が高い状態です。
FATL、FTLM と RBCI インジケーターが同期的に動いている場合、トレードします。 ダマシシグナルは、STLM インジケーターによって除外されます (その絶対値は大きくなるか、変化しません)。 STLM が落下した場合、 SATL と RSTL の収束を示します。 同時に、弱気のシグナルを RBCI が受信すると、相場が売られ過ぎている場合はチェックされます。 相場参入価格は、足の始値と同等かよりも優れています。
- このシグナルは、RBCI インデックスによって決定された特定の周波数帯のアクティブサイクルの合計に基づいています。 STLM 線の方向と RSTL との SATL の収束/発散は無視されます。 STLM の値が正または負の場合は、主なトレンドは、相場で形成される方向を示しています。 FATL ラインの方向と動作は、追加のフィルタとして機能します。
このシグナルは、複合波周期が、中立または下降する長期的なトレンドにおいて、強い買われ過ぎ領域のローカル最小値に達すると形成されます。 レンジでは、相場のサイクルによって引き起こされる可能性は、ボラティリティによって引き起こされる可能性よりも高くなります。 トレンドが形成されれば、相場周期に基づく潜在性は長期トレンドの潜在性となります。
トレード開始価格は、シグナルの足に続く足の始値と同等かそれより優れています。
- シグナルの基礎は2つの相違です。つまり、 RBCI の動きの方向と FATL ラインの間で、RBCI および FTLM の間と同様です。 FATL と RBCI と FTLM のインデックスが一定期間内に異なる方向に移動すると、スタンバイフェーズがアクティブになります。 弱気シグナル-ローカル FTLM 最小、FATL と RBCI は、その動きの方向を変更しません。 チャートでは、 FATL の方向に FTLM の "うなずく” ように見えます。
このシグナルは、"速い" 下降トレンドの終点の近くで見られます (FTLM 値は、"0" の近くにあります)。 このシステムは短いトレンドの動きにかなり正確なシグナルを形作ります。
トレンドの反転の前の、主要なシグナルです。
相場参入価格は、シグナルロウソク足に続くロウソクの始値と同等またはそれよりも優れて選択されています。
- シグナルは長いトレンドの間に形作られる。 RBCI と PCCI のインデックスは、相場の買われ過ぎラインに同時に到達します (下降トレンドの場合)。 このようなシグナルは、多くの場合、トレンドの最後の段階で形成され、クオートは、急速に反対方向に移動します。
相場参入価格も、シグナルのロウソクの後に表示されるロウソクの始値よりも同等またはより良い選択されています。
- 長期的な弱気のトレンドが形成されている場合 (SATL はすでに下落しているが、STLM 値はまだポジティブである)、PCCI 指数は 100 (相場買わローカル) の上の値に達します。 反転シグナルは、トレンドが形成される瞬間、高い相場のボラティリティに基づいています。
相場参入価格は、シグナルロウソク足に続くロウソクの始値と同等またはそれよりも優れて選択されています。
- 最も強いトレンドの逆転シグナルは FATL ラインが SATL ラインによって下方に壊れた後、最初のテクニカルな上向きの修正が終わった後観察できます。 この後売ります。 このテクニカルの修正の終了は、FATL のローカル最大値によって示されます。
売り価格は、シグナルのロウソクに続くロウソクの始値よりも高いか等しいです。
- そして最後に、別の反転シグナルは、2つのクロスが同時に起こるときに形成されます。つまり、 "高速" と "低速" アダプティブライン FATL と SATL だけでなく、FATL と RFTLです。 このシグナルは、古い弱体化トレンドの鋭いブレイクの瞬間を示しています。 売り価格は、シグナルのロウソクに続くロウソクの始値よりも高いか等しいです。
2. ローパスフィルタの構築
戦略の主な側面を概説し、実用的な部分に進みましょう。 もちろん、このようなフィルタは、戦略の基礎であるため、ローパスフィルタを構築することによって、このタスクを開始します。
ローパスフィルタを構築するには、カットオフ周波数と減衰の主なパラメータを定義する必要があります。 そして、もし作者がフィルターが少なくとも40dB のストップ帯で減衰を定義するべきだと告げれば、遮断周波数を決定するために価格データのスペクトル分析が必要になります。
以上のように、筆者は最大エントロピー法を用いてパワースペクトル密度を推定しました。 このメソッドは、パラメトリックメソッドに属しており、数学的なモデルに従って実行されます。 数学的モデルは、回帰メソッドを使用して構築されます。
2.1. パワースペクトル密度の解析
CSpertrum クラスは、スペクトル密度を推定するために作成されます (コード全体は、添付ファイルにあります)。 初期化中に、ツール名、タスク時間、分析対象の足数が渡されます。
class CSpectrum { private: int ci_HistoryBars; //分析の足 string cs_Symbol; //シンボル ENUM_TIMEFRAMES ce_Timeframe; //タイムフレーム double cda_AR[]; //回帰係数 int ci_NumberCoeffs; //係数の数 public: CSpectrum(int bars=2880, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_CURRENT); ~CSpectrum(); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CSpectrum::CSpectrum(int bars=2880, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_CURRENT) { ci_HistoryBars = bars; cs_Symbol = (symbol==NULL ? _Symbol : symbol); ce_Timeframe = period; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CSpectrum::~CSpectrum() { }
自己回帰関数とパワースペクトル密度関数の計算は、 Victorが提案するメソッドに従って行います。 アルゴリズムの詳細に関心のある方は、この記事を読むことをお勧めします。 領域スペクトル解析関数の結果はデータの配列であり、わかりやすいようにグラフとして表現することができます。
チャート上のアウトバーストは、一定の周波数でのシグナルパワーの増加を示しています。 アウトバーストは、フィルタの周波数を決定するために必要です。 これを行うには、CSpecrum クラスにパブリック関数 GetPeriods を追加し、呼び出されたときに FATL と SATL の期間を返します。
この関数の内部では、アウトバーストはフラクタルとして定義されます。 SATL フィルタの期間については、最も低い周波数でインパルスを示す最初のバーストを決定します。 FATL に、小さい振幅および高周波が付いている「ノイズ」の衝動を取除く最も高い頻度および力の40dB より大きいインパルスを見つけます。 この関数がフィルタの期間を見つけることができない場合は、false を返します。
bool CSpectrum::GetPeriods(int &FAT,int &SAT) { if(!Spectrum()) return false; FAT=SAT=0; int total=ArraySize(cad_Spectr)-1; for(int i=1;(i<total);i++) { int temp=2*(total+1)/i; if(cad_Spectr[i]==0 || temp>(int)ci_HistoryBars/4) continue; if((cad_Spectr[i]-cad_Spectr[i+1])>=0 && (cad_Spectr[i]-cad_Spectr[i-1])>0) { if(SAT==0) SAT=temp; else { if(cad_Spectr[i]<-40) { if(FAT==0) FAT=temp; break; } if(temp>=20) FAT=temp; } } } if(SAT==0 || FAT==0) return false; return true; }
2.2. ローパスフィルタの係数を計算します。
フィルタの周波数が決定されるので、ローパスフィルタを構築します。 デジタルフィルタの一般式は次のとおりです。
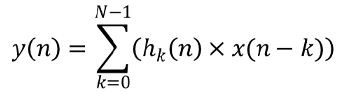
ここで、 y —フィルタ出力;x —ソースデータの配列。hk —インパルス応答;N —インパルス応答の数です。
価格データはソースデータとして機能し、インパルス応答の数はナイキスト間隔に等しく設定されます。 インパルス応答自体はまだ計算されていません。 ローパスフィルタの理想的なインパルス応答は、数式を使用して計算することができます。
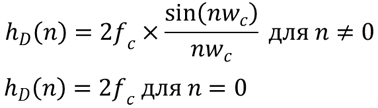
fc とwc は、カットオフ周波数です。
残念ながら、我々の世界は理想状態から遠く離れています。 したがって、"本物" のインパルス応答が必要です。 計算には重み関数w (n)が必要です。 重量関数には種類があります。 ここでは、ブラックマン関数を使用します。
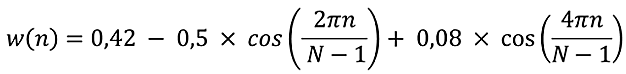
ここで、 Nはフィルタ要素の数です。
「本物」のインパルス応答を得るためには、対応する重み関数で理想的なインパルス応答を乗算する必要があります。
![]()
計算式が定義されたので、インパルス応答が計算され、インプットデータがフィルタ処理される CFLF クラスを作成してみましょう。 インパルス応答の係数を計算するには、フィルタリング期間に渡されるパブリック関数 CalcImpulses を作成してみましょう。 次に、関数アルゴリズムは、上記の数式を繰り返します。 その後、インパルス応答を正規化し、その合計を "1" にします。
bool CFLF::CalcImpulses(int period) { if(period<20) return false; int N=(int)(period/2); if(ArraySize(cda_H)!=N) if(ArrayResize(cda_H,N)<N) return false; double H_id[],W[]; if(ArrayResize(H_id,N)<N || ArrayResize(W,N)<N) return false; cd_Fs=1/(double)period; for (int i=0;i<N;i++) { if (i==0) H_id[i] = 2*M_PI*cd_Fs; else H_id[i] = MathSin(2*M_PI*cd_Fs*i )/(M_PI*i); W[i] = 0.42 - 0.5 * MathCos((2*M_PI*i) /( N-1)) + 0.08 * MathCos((4*M_PI*i) /( N-1)); cda_H[i] = H_id[i] * W[i]; } //正規化 double SUM=MathSum(cda_H); if(SUM==QNaN || SUM==0) return false; for (int i=0; i<N; i++) cda_H[i]/=SUM; //1に等しい係数の合計 //--- return true; }
2.3. インジケーターの計算 FATL, SATL, RTFL, RSTL.
インパルス応答が得られたら、インパルスインジケーター値の計算に進むことができます。 フィルタクラスから直接 FATL、SATL、RFTL、RSTL の各インジケーターの値を取得すると便利です。
クラスのさまざまなインスタンスが高速、低速フィルターに使用されるため、AdaptiveTrendLine関数と ReferenceTrendLine 関数を作成するだけで十分です。 この関数は、現在のロウソクに相対的に使用されるツール、時間枠とシフトに渡されます。 この関数は、フィルター処理された値を返します。
ReferenceTrendLine 関数は基本的に AdaptiveTrendLine 関数と同じであることに注意してください。 唯一の差は、ReferenceTrendLine がナイキスト期間のシフト値で計算されることです。 したがって、ReferenceTrendLine はナイキスト期間を計算し、現在の足に対する適切なシフトを指定して AdaptiveTrendLine を呼び出します。
double CFLF::AdaptiveTrendLine(string symbol=NULL,ENUM_TIMEFRAMES timeframe=0,int shift=1) { string symb=(symbol==NULL ? _Symbol : symbol); int bars=ArraySize(cda_H); double values[]; if(CopyClose(symb,timeframe,shift,bars,values)<=0) return QNaN; double mean=MathMean(values); double result=0; for(int i=0;i<bars;i++) result+=cda_H[i]*(values[bars-i-1]-mean); result+=mean; return result; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CFLF::ReferenceTrendLine(string symbol=NULL,ENUM_TIMEFRAMES timeframe=0,int shift=1) { shift+=(int)(1/(2*cd_Fs)); return AdaptiveTrendLine(symbol,timeframe,shift); }
使用される他のインジケーターは、得られた値の導関数であり、以下で計算されます。
3. MQL5 ウィザード用のトレーディングシグナルモジュールの作成
今回は、通常の執筆方法から脱線し、МetaТrader 5 でMQL ウィザードの存在について考慮します。 この便利な関数は、あらかじめモジュールのエキスパートをアセンブルするコンストラクタの一種です。 新しいEAを作成したり、新関数を追加したり、未使用のものを削除したりできます。 したがって、このようなモジュールに、EAの意思決定アルゴリズムを組み込むことをお勧めします。 このメソッドは、すでに何度も考察されています [4]、[5]。 したがって、この記事では、戦略に関連する側面のみを考慮します。
まず、CExpertSignal に基づいて CSignalATCF シグナルクラスを作成し、その中に以前に作成されたクラスを含めることから始めましょう。
class CSignalATCF : public CExpertSignal { private: CSpectrum *Spectrum; //スペクトル計算のクラス CFLF *FFLF; //高速低周波フィルタのクラス CFLF *SFLF; //低速低周波フィルタのクラスpublic: CSignalATCF(); ~CSignalATCF(); };
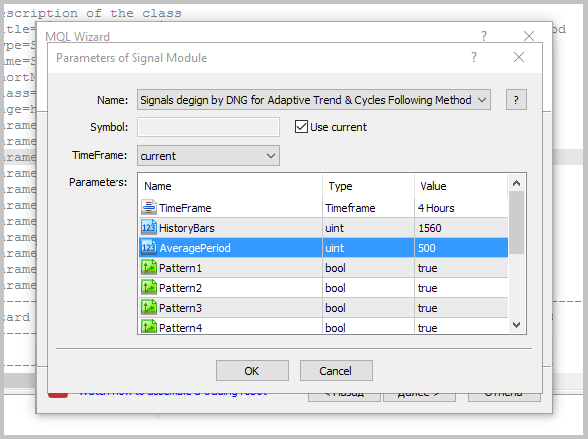
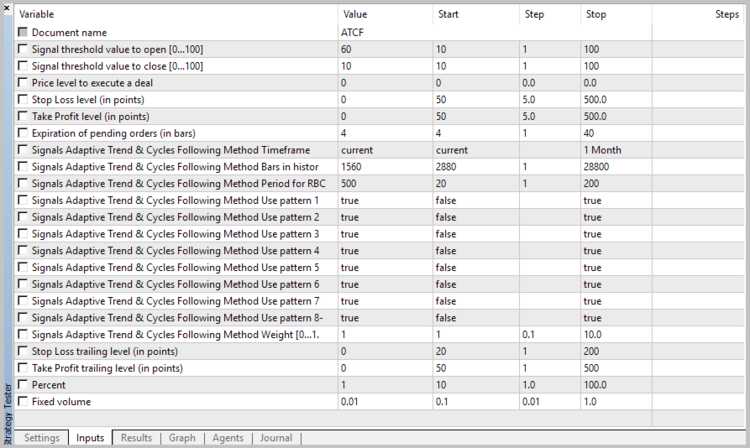
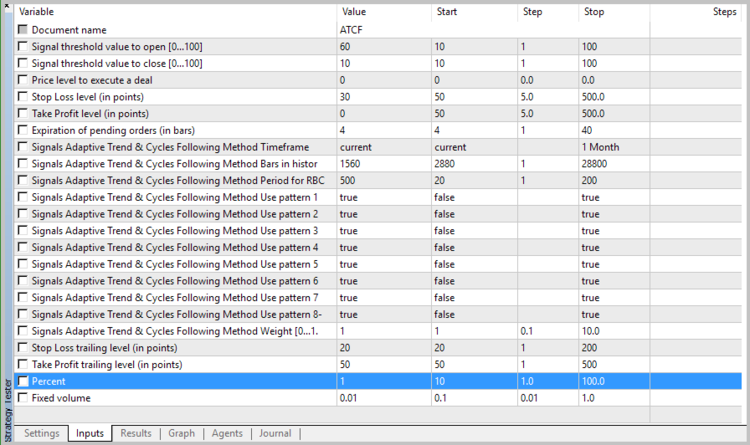
初期化時には、モジュールをツール名、使用されたタイムフレーム、パワースペクトル密度解析の履歴の足数、平均の足数 (RBCI および PCCI インジケーターの計算に使用) を渡す必要があります。). さらに、どのパターンを開始ポジションに使用するかを指定する必要があります。 モジュールの説明の一般的な外見は、次のようになります。
//--- wizard description start //+---------------------------------------------------------------------------+ //| Description of the class | //| Title=Signals design by DNG for Adaptive Trend & Cycles Following Method | //| Type=SignalAdvanced | //| Name=Signals Adaptive Trend & Cycles Following Method | //| ShortName=ATCF | //| Class=CSignalATCF | //| Page=https://www.mql5.com/ru/articles/3456 | //| Parameter=TimeFrame,ENUM_TIMEFRAMES,PERIOD_H4,Timeframe | //| Parameter=HistoryBars,uint,1560,Bars in history to analysis | //| Parameter=AveragePeriod,uint,500,Period for RBCI and PCCI | //| Parameter=Pattern1,bool,true,Use pattern 1 | //| Parameter=Pattern2,bool,true,Use pattern 2 | //| Parameter=Pattern3,bool,true,Use pattern 3 | //| Parameter=Pattern4,bool,true,Use pattern 4 | //| Parameter=Pattern5,bool,true,Use pattern 5 | //| Parameter=Pattern6,bool,true,Use pattern 6 | //| Parameter=Pattern7,bool,true,Use pattern 7 | //| Parameter=Pattern8,bool,true,Use pattern 8 | //+---------------------------------------------------------------------------+ //---ウィザードの説明の終わり
ここで、必要な変数と関数を宣言します。
class CSignalATCF : public CExpertSignal { private: ENUM_TIMEFRAMES ce_Timeframe; //タイムフレーム uint ci_HistoryBars; //分析へのヒストリーの棒 uint ci_AveragePeriod; //RBCI と PCCI の期間 CSpectrum *Spectrum; //スペクトル計算のクラス CFLF *FFLF; //高速低周波フィルタのクラス CFLF *SFLF; //低速低周波フィルタのクラス //---インジケーターデータ double FATL, FATL1, FATL2; double SATL, SATL1; double RFTL, RFTL1, RFTL2; double RSTL, RSTL1; double FTLM, FTLM1, FTLM2; double STLM, STLM1; double RBCI, RBCI1, RBCI2; double PCCI, PCCI1, PCCI2; //---パターンフラグ bool cb_UsePattern1; bool cb_UsePattern2; bool cb_UsePattern3; bool cb_UsePattern4; bool cb_UsePattern5; bool cb_UsePattern6; bool cb_UsePattern7; bool cb_UsePattern8; //--- datetime cdt_LastSpectrCalc; datetime cdt_LastCalcIndicators; bool cb_fast_calced; bool cb_slow_calced; bool CalculateIndicators(void); public: CSignalATCF(); ~CSignalATCF(); //--- void TimeFrame(ENUM_TIMEFRAMES value); void HistoryBars(uint value); void AveragePeriod(uint value); void Pattern1(bool value) { cb_UsePattern1=value; } void Pattern2(bool value) { cb_UsePattern2=value; } void Pattern3(bool value) { cb_UsePattern3=value; } void Pattern4(bool value) { cb_UsePattern4=value; } void Pattern5(bool value) { cb_UsePattern5=value; } void Pattern6(bool value) { cb_UsePattern6=value; } void Pattern7(bool value) { cb_UsePattern7=value; } void Pattern8(bool value) { cb_UsePattern8=value; } //---設定の検証メソッド virtual bool ValidationSettings(void); //---インジケーターと時系列を作成するメソッド virtual bool InitIndicators(CIndicators *indicators); //---相場モデルが形成されているかどうかをチェックするメソッド virtual int LongCondition(void); virtual int ShortCondition(void); };
インジケーター値を計算するための関数を作成します。
boolCSignalATCF:: CalculateIndicators (void) { //---最後の計算の時間をチェック datetime current=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE); if(current==cdt_LastCalcIndicators) return true; //この足でデータが既に計算されている場合は終了 //---スペクトルの再計算の確認 MqlDateTime Current; TimeToStruct(current,Current); Current.hour=0; Current.min=0; Current.sec=0; datetime start_day=StructToTime(Current); if(!cb_fast_calced || !cb_slow_calced || (!PositionSelect(m_symbol.Name()) && start_day>cdt_LastSpectrCalc)) { if(CheckPointer(Spectrum)==POINTER_INVALID) { Spectrum=new CSpectrum(ci_HistoryBars,m_symbol.Name(),ce_Timeframe); if(CheckPointer(Spectrum)==POINTER_INVALID) { cb_fast_calced=false; cb_slow_calced=false; return false; } } int fast,slow; if(Spectrum.GetPeriods(fast,slow)) { cdt_LastSpectrCalc=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE); if(CheckPointer(FFLF)==POINTER_INVALID) { FFLF=new CFLF(); if(CheckPointer(FFLF)==POINTER_INVALID) return false; } cb_fast_calced=FFLF.CalcImpulses(fast); if(CheckPointer(SFLF)==POINTER_INVALID) { SFLF=new CFLF(); if(CheckPointer(SFLF)==POINTER_INVALID) return false; } cb_slow_calced=SFLF.CalcImpulses(slow); } } if(!cb_fast_calced || !cb_slow_calced) return false; //エラーで終了 //---インジケーターデータの計算 int shift=StartIndex(); double rbci[],pcci[],close[]; if(ArrayResize(rbci,ci_AveragePeriod)<(int)ci_AveragePeriod || ArrayResize(pcci,ci_AveragePeriod)<(int)ci_AveragePeriod || m_close.GetData(shift,ci_AveragePeriod,close)<(int)ci_AveragePeriod) { return false; } for(uint i=0;i<ci_AveragePeriod;i++) { double fatl=FFLF.AdaptiveTrendLine(m_symbol.Name(),ce_Timeframe,shift+i); double satl=SFLF.AdaptiveTrendLine(m_symbol.Name(),ce_Timeframe,shift+i); switch(i) { case 0: FATL=fatl; SATL=satl; break; case 1: FATL1=fatl; SATL1=satl; break; case 2: FATL2=fatl; break; } rbci[i]=fatl-satl; pcci[i]=close[i]-fatl; } RFTL=FFLF.ReferenceTrendLine(m_symbol.Name(),ce_Timeframe,shift); RSTL=SFLF.ReferenceTrendLine(m_symbol.Name(),ce_Timeframe,shift); RFTL1=FFLF.ReferenceTrendLine(m_symbol.Name(),ce_Timeframe,shift+1); RSTL1=SFLF.ReferenceTrendLine(m_symbol.Name(),ce_Timeframe,shift+1); RFTL2=FFLF.ReferenceTrendLine(m_symbol.Name(),ce_Timeframe,shift+2); FTLM=FATL-RFTL; STLM=SATL-RSTL; FTLM1=FATL1-RFTL1; STLM1=SATL1-RSTL1; FTLM2=FATL2-RFTL2; double dev=MathStandardDeviation(rbci); if(dev==0 || dev==QNaN) return false; RBCI=rbci[0]/dev; RBCI1=rbci[1]/dev; RBCI2=rbci[2]/dev; dev=MathAverageDeviation(pcci); if(dev==0 || dev==QNaN) return false; PCCI=pcci[0]/(dev*0.015); PCCI1=pcci[1]/(dev*0.015); PCCI2=pcci[2]/(dev*0.015); cdt_LastCalcIndicators=current; //--- return true; }
次に、対応する重みづけを指定して、ポジションの開始と決済のパターンを記述します (40で決済 80でオープン)。 下記はロングポジションを開くための関数です。 ショートポジションの関数は同様に整理されます。
intCSignalATCF:: LongCondition (void) { if(!CalculateIndicators() || m_open.GetData(1)>m_close.GetData(1)) return 0; int result=0; //---閉じる if(m_high.GetData(2)<m_close.GetData(1) || (STLM1<=0 && STLM>0) || (PCCI1<PCCI && PCCI1<=PCCI2) || (RBCI>RBCI1 && RBCI1>=RBCI2 && RBCI1<-1) || (RBCI1<=0 && RBCI>0)) result=40; //---パターン1 if(cb_UsePattern1 && FTLM>0 && STLM>STLM1 && PCCI<100) result=80; else //---パターン2 if(cb_UsePattern2 && STLM>0 && FATL>FATL1 && FTLM>FTLM1 && RBCI>RBCI1 && (STLM>=STLM1 || (STLM<STLM1 && RBCI<1))) result=80; else //---パターン3 if(cb_UsePattern3 && STLM>0 && FATL>FATL1 && RBCI>RBCI1 && RBCI1<-1 && RBCI1<=RBCI2 && FTLM>FTLM1) result=80; else //---パターン4 if(cb_UsePattern4 && SATL>SATL1 && FATL>FATL1 && RBCI>RBCI1 && FTLM<FTLM1 && FTLM2<=FTLM1) result=80; else //---パターン5 if(cb_UsePattern5 && SATL>SATL1 && STLM>=0 && PCCI1<=-100 && PCCI1<PCCI && PCCI>-100 && RBCI>RBCI1 && RBCI1<=RBCI2 && RBCI1<-1) result=80; else //---パターン6 if(cb_UsePattern6 && SATL>SATL1 && STLM<0 && PCCI1<=-100 && PCCI>-100) result=80; else //---パターン7 if(cb_UsePattern7 && FATL>FATL1 && FATL1<=SATL1 && FATL>SATL && FATL1<=FATL2) result=80; //---パターン8 if(cb_UsePattern8 && FATL>FATL1 && FATL1<=SATL1 && FATL>SATL && FATL1<=RFTL1 && FATL>RFTL) result=80; return result; }
4. アダプティブ・マーケットによるエキスパート・アドバイザーの作成
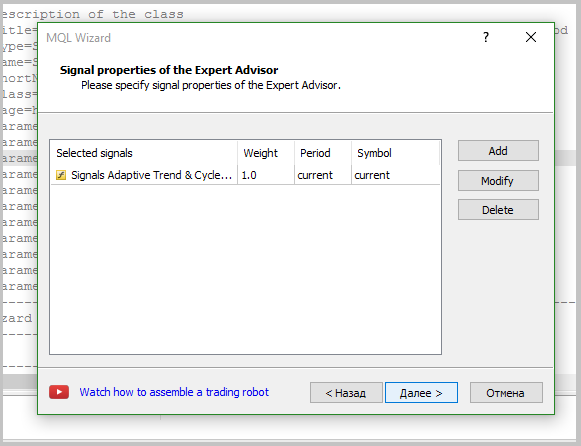
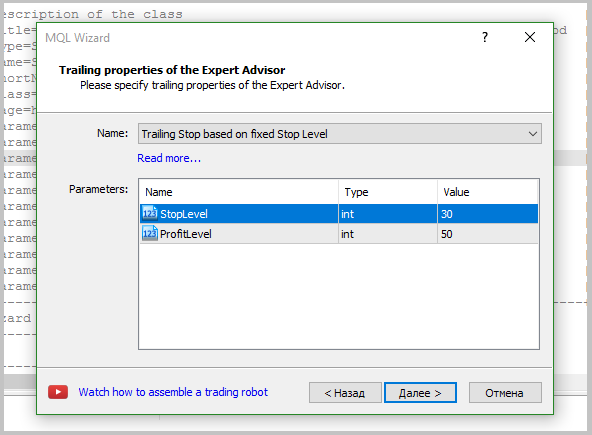
シグナルモジュールを作成した後、EAの生成に進むことができます。 この記事では、ウィザードを使用してEAを作成するプロセスについて詳しく説明します。 EA を作成する際には、上記で説明したトレーディングシグナルモジュールのみが使用されました。 さらに、固定数ポイントのトレーリングストップを追加しました。 固定ロットは、生成されたシグナルの品質を評価できるようにする戦略をテストするときに使用されます。
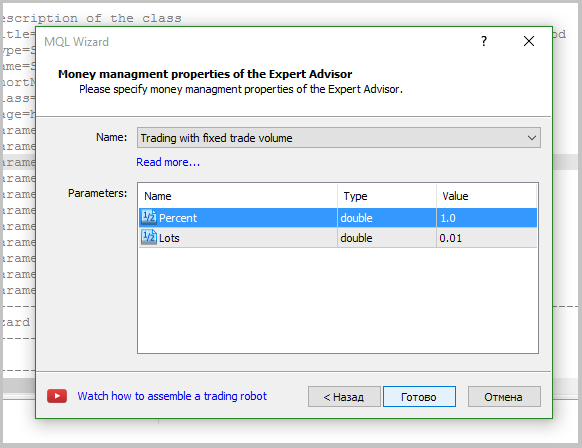
5. EAをテスト。
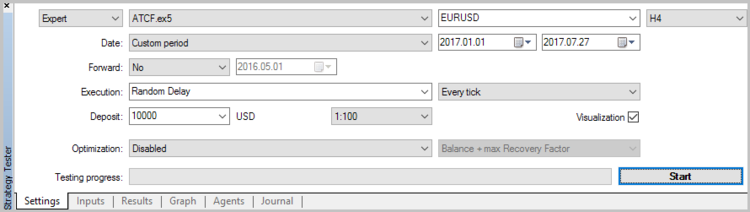
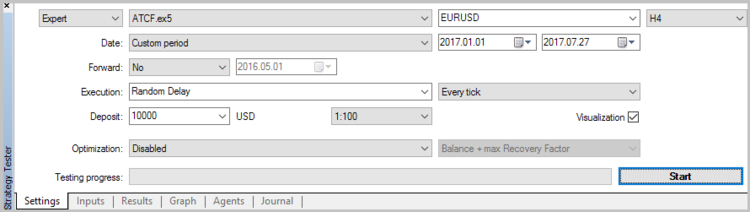
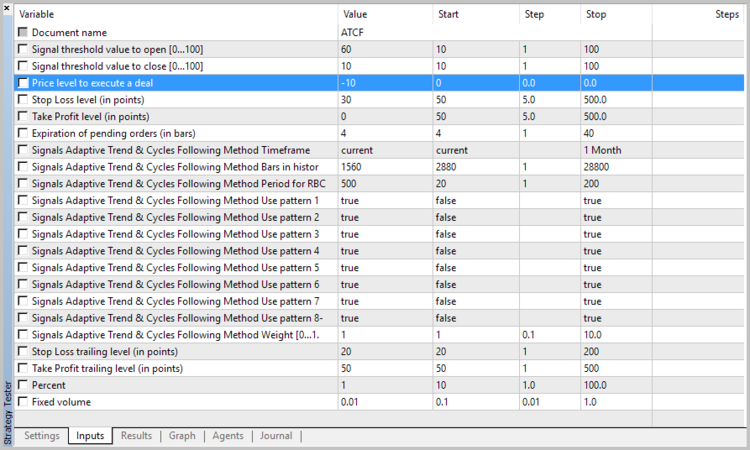
エキスパートアドバイザを作成したら、ストラテジーテスターでアダプティブ相場の次のメソッドをテストすることができます。 テスト時には、レベル60でポジションを開くための重みづけを設定します。
5.1. ストップロス、テイクプロフィット、トレーリングストップを使用せずにテスト。
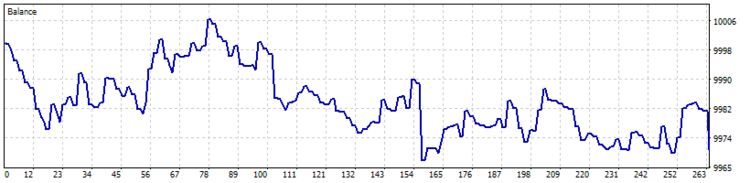
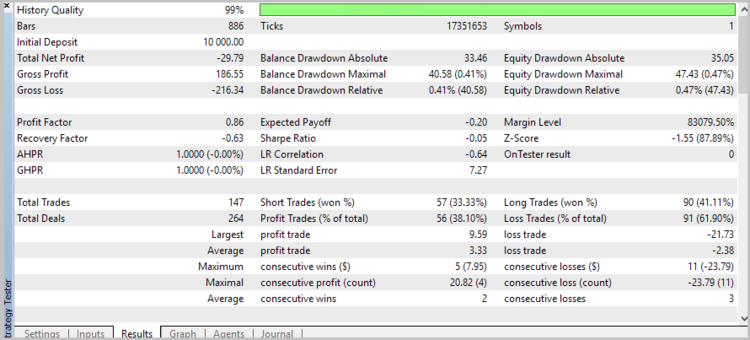
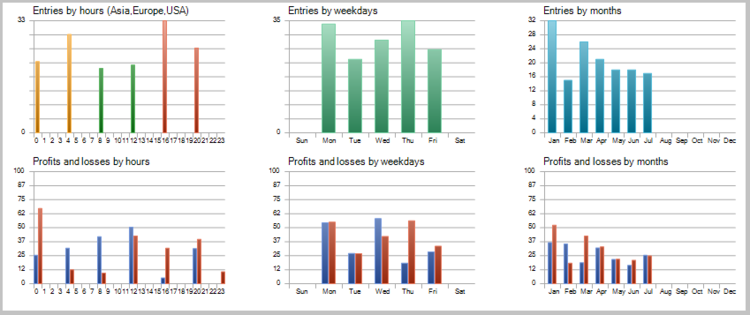
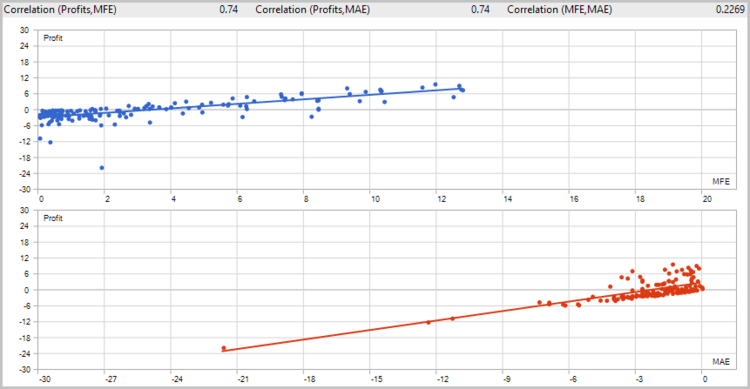
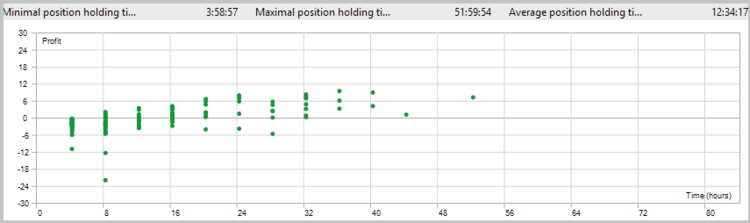
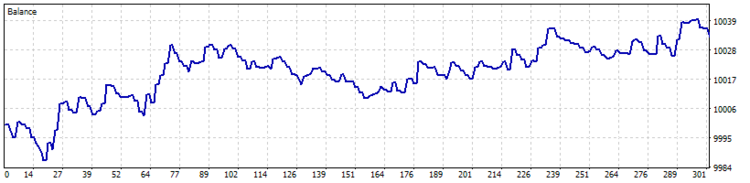
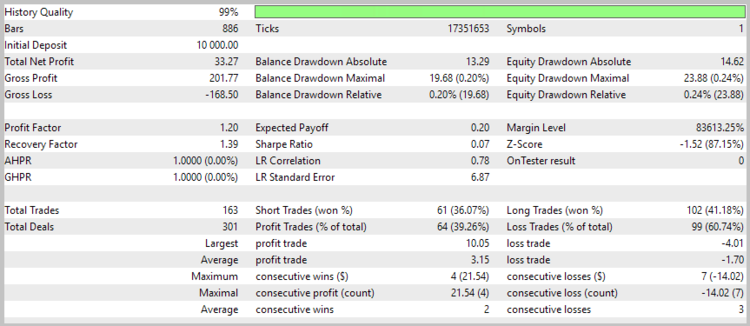
EA によって生成されたシグナルの品質を推定するために、最初のテストの実行は、ストップロスなどを使用せずに実行しました。 2017の7ヶ月間、H4 のタイムフレームでテストを実施しています。
残念ながら、最初のテストでは、ストップロスを使用せずに戦略が良くないことが分かりました。
価格チャート上のトレード分析は、2つの弱点を示しました。
- このEAは、潜在的に有益なトレードの損失決済につながるトレードを閉じることができません。
- このEA は、大きな動きをよく処理しますが、平らな動きの間に多くのマイナスの取引を行います。
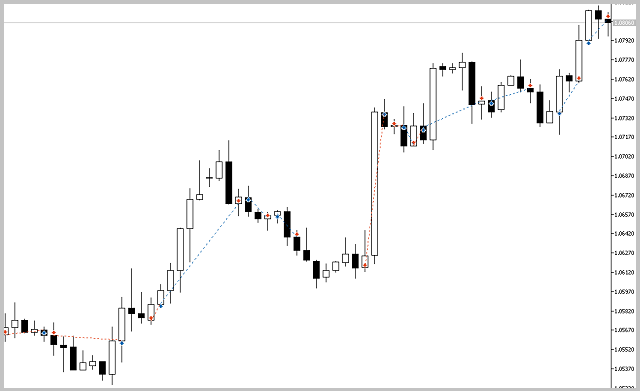
5.2. ストップロスとトレーリングストップを使用してテスト。
最初のポイントの損失を最小限に抑えるために、ストップロスとトレーリングストップを適用しました。
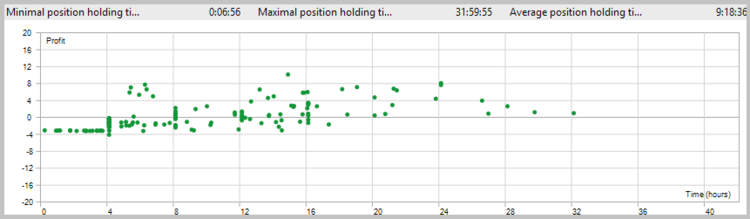
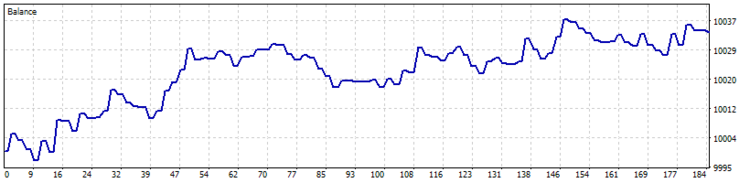
第2テストの結果は、ポジション保持時間の減少、収益性の高いトレード比率の微増、利益に対する一般的な傾向が分かりました。
もかかわらず、マイナストレードは 39.26% でした。 そして、2番目の問題はまだ存在していた (レンジ相場で損失が増える)。
5.3. ストップオーダーを使用してテスト。
一連のマイナストレードに伴う損失を削減するため、ストップオーダーを使用したテストを実施しました。
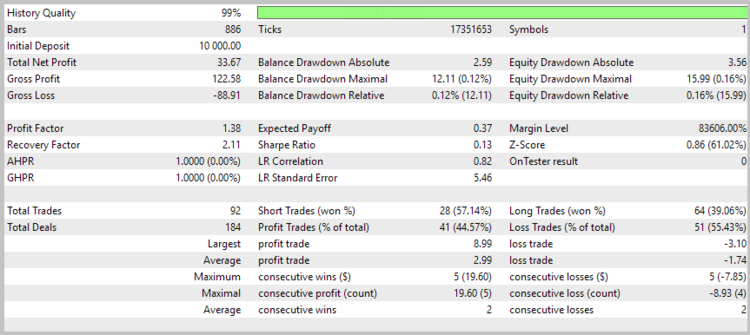
3回目のテスト稼働の結果、トレード数はほぼ半減したもの、総利益が増加し、収益性の高いトレードのシェアは 44.57% に増加しました。
結論
この記事は適応性があるメソッドを考察しました。 テスト結果により、この戦略の可能性を示しているが、特定のボトルネックは、実際の相場で使用できるようにするために排除する必要があります。 それもかかわらず、このメソッドは実行可能です。 ソースファイルとテスト結果は、添付されています。
リファレンス
- "Vladimir Kravchuk"、12月 2000-6 月2001。
- 時系列の主な特徴の分析。
- メタトレーダー5の価格インジケーターAR
- MQL5 ウィザード: トレーディングシグナルのモジュールを作成するメソッド
- 6ステップで独自のトレーディングロボットを作成!
- MQL5 ウィザード: 新しいバージョン
この記事で使用されるプログラム:
| # | 名前 | タイプ | 詳細 |
|---|---|---|---|
| 1 | Spectrum.mqh | クラスライブラリ | 解析されたツールのパワースペクトル密度を推定するためのクラス |
| 2 | FLF.mqh | クラスライブラリ | ローパスフィルタを構築し、初期データをフィルタリングするためのクラス |
| 3 | SignalATCF.mqh | クラスライブラリ | 適応型相場に基づくトレードシグナルモジュールの提案 |
| 4 | ATCF.mq5 | EA | 適応相場に基づくEA |
| 5 | ACTF_Test.zip | Archive | アーカイブには、ストラテジーテスターで EA をテストした結果があります。 |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/3456
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 バランスグラフを使用した戦略の最適化と、結果の「バランス+最大シャープレシオ」基準との比較
バランスグラフを使用した戦略の最適化と、結果の「バランス+最大シャープレシオ」基準との比較
 クロスプラットフォームEA: CExpertAdvisor と CExpertAdvisors クラス
クロスプラットフォームEA: CExpertAdvisor と CExpertAdvisors クラス
 古典的な隠れたダイバージェンスを解釈する新しいアプローチ
古典的な隠れたダイバージェンスを解釈する新しいアプローチ
 拡散と収束の自動探索
拡散と収束の自動探索
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
ユーリ、開かないのはいいことだ。過去のデータ(一般集団からの現在のサンプルと混同しないでほしい。多くの人は、サンプルを分析すれば、すでに歴史を分析していると思っている。- いいえ、そうではありません)、すなわち平均化された過去の係数やパラメーターは、どこにも行けない道なのです。このような記事を書いている人のほとんどは、FXに限らず、起こっているプロセスの本質について非常に曖昧な考えを持っているようだ。繰り返しになるが、ばかげた数字を分析し、現在のトレンドとの一致を探す人々は、逆説的に聞こえるかもしれないが、 これらの記事よりもはるかに真実に近い。
でも、理論物理学に関係する人に話を聞けば、5分もあればFXのプロセスの本質についてすべてを教えてくれるだろう。このような人が本物の物理学者である。彼らは決してお金を追いかけない。それだけだ!それ以外はありえない。
この場合、あなたはデータのサンプルではなく、選択した期間における過去のデータを分析している。サンプルとヒストリカルデータの違いは、すべてのデータを取っているわけではなく、全データセットから無秩序に選択されたデータだけを取っている点である。
もし記事に具体的な誤りがあれば、指摘してほしい。私は議論を歓迎する。
この場合、分析されるのは、データのサンプルではなく、選択された期間の履歴データである。サンプリングとヒストリカルデータの違いは、全データを採取するのではなく、全データから無作為に選択したデータのみを採取する点である。
記事に具体的な誤りがあれば、指摘してほしい。議論に応じます。
こんにちは、ドミトリー!
おそらく計算に間違いはないでしょう。私は、明らかに無線エンジニアとしてのあなたの才能と能力を貶めたいわけではありません。
ただ、あなたはまだ自分が取り組んでいることを理解していないのだと思います。どんな関数ですか?フーリエ変換を何に適用しているのか?例えば、フォッカー・プランク方程式の確率密度 関数やシュレーディンガーの波動関数に あなたの好きな変換を適用してみてください。そうすれば我々は喜ぶだろう。
もう一度言うが、物理学のある分野での強みが、別の分野での結果を生むわけではない。例えば、私の時代の物理学部のラジオエレクトロニクスのコースはちょうど1学期でしたが、フーリエ変換の崇拝者たちはその後もこの専門分野の研究を続け、ラジオ工学の分野で高みに達しました。ここが彼らの知識が役に立たないところだ。ここでは抽象的な思考が必要なのだ。
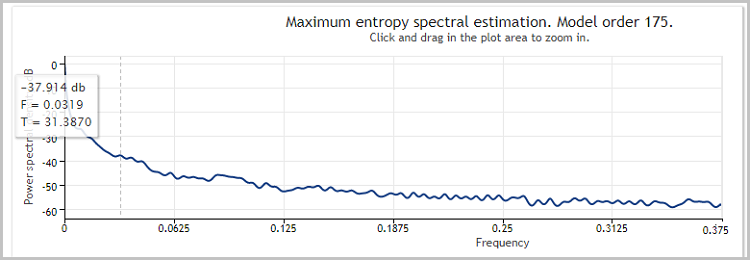
私は、重要な頻度を決定する公式には同意できない。
あなたの例では、市場データに基づくと、このようになる:
点線の周波数は隣接する周波数よりも高いが、左側の周波数(隣接する周波数を除く)よりもはるかに低い。つまり、左側の周波数はより頻度が高く、したがってより重要であり、それらをフィルタリングすべきではない。
本来は、0から-40dbとの交点までの周波数を取るべきである。0は確かに論理的でなく、0に非常に近いが、これは非常に多くのバーを考慮しなければならないからである。
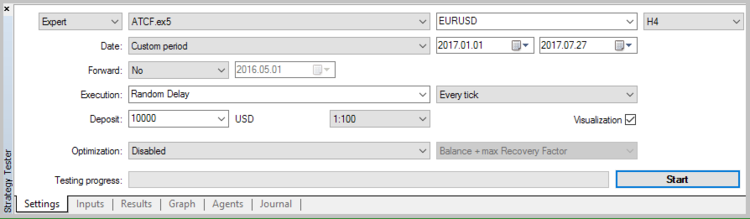
また、ノイズの多い正弦波の記事のような状況があると仮定する:
すなわち、支配的な周波数/周波数が本当に存在する場合、各点を隣接する点だけでなく、すべての点と比較して極値を探索する必要があります。
一般的に、あなたは興味深いツールを作ってくれました。ありがとうございます。
私は知っている。
あなたは知らないだけでなく、自分の書いたものを信じていない。知っていたら書かないだろうから。
著者はコードと記事を書き、賢くなった。彼は報酬を得て、200ドルを100万ドルに近づけた。しかし、あなたとあなたの固定観念は違う。