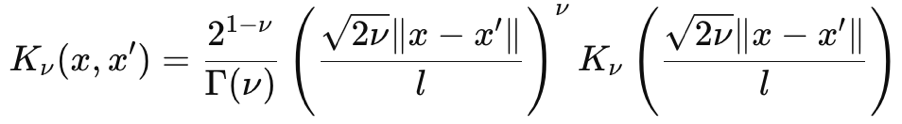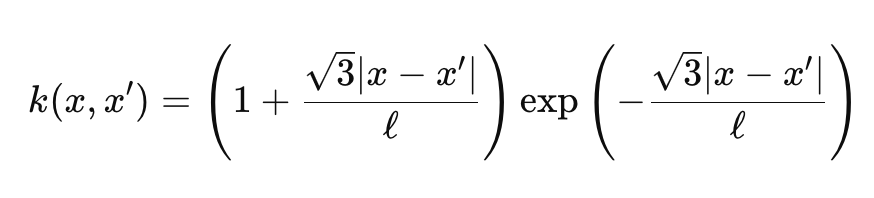知っておくべきMQL5ウィザードのテクニック（第37回）：線形カーネルとMatérnカーネルによるガウス過程回帰

はじめに

2つのガウス過程カーネルを考慮し、ウィザードで組み立てられたエキスパートアドバイザー(EA)の主要コンポーネントクラスを実装するさまざまな方法についての連載を続けます。対象となるカーネルは、線形カーネルとMatérnカーネルです。前者は非常に単純なため、Wikipediaのページは見つかりませんが、後者についてはこちら（英語）に参照ページがあります。 

以前説明したガウス過程カーネル(GP)についてまとめると、GPは関係するデータセットのペアに関する機能的または事前の知識がなくても、データセット間の複雑な関係(通常はベクトル形式)をマッピングできるノンパラメトリックモデルです。このため、GPは、関係するデータセットが非線形またはノイズが多い状況の処理に最適です。さらに、この柔軟性により、GPは微妙な出力を出す傾向があるため、変動しやすい金融時系列にも適しています。GPは予測推定値と信頼区間を提供し、2つのデータセット間の類似性を判断するのに役立ちます。ガウス過程回帰では複数の種類のカーネルを使用できるため、特にカーネルを使用して予測を外挿する場合は、適切なカーネルを特定するか、選択したカーネルの欠点に注意することが重要です。

以下は、本連載でこれまでに紹介したカーネルとその特徴の一部をまとめた表です。

カーネルタイプ	最適	説明
線形カーネル	トレンド	時間の経過に伴う線形傾向を捉えます。長期的な価格の上昇または下降を示す資産に最適です。シンプルで計算効率は高いですが、線形関係を前提としています。
動径基底関数(RBF)カーネル	トレンドとボラティリティ	緩やかな価格変動を伴う、スムーズで長期的なトレンドを捉えるのに最適です。スムーズな推定値を提供し、継続的なパターンに適しています。ただし、急激な変化や極端なボラティリティには対応できません。
Matérnカーネル	トレンド、ボラティリティ、サイクル	より粗く、より滑らかでないトレンドやボラティリティの突然の変化を捉えることができます。パラメータ ν は滑らかさを制御します。ν が低いと粗いボラティリティを捉え、ν が高いとトレンドが滑らかになります。

外挿する時系列に応じて、その長所に基づいて適切なカーネルを選択する必要があります。金融時系列は、周期的または循環的な動作を示すことが多く、以下で紹介するMatérnなどのカーネルは、これらの関係をマッピングするのに役立ちます。さらに、この最初の記事でRBFで見たように、不確実性を定量化することは、取引者が横ばいまたは急激な市場に直面したときに大きな恩恵をもたらす可能性があります。RBFなどのカーネルは、ポイント推定値を提供するだけでなく、信頼区間も提供し、このような状況で役立ちます。これは、信頼区間が弱いシグナルをふるいにかけるのに役立つと同時に、不確実な環境での主要な転換点を強調するのに役立つためです。

平均回帰データセットは、Ornstein-Uhlenbeckなどの特殊なカーネルで処理することもできます。これについては、今後の記事で取り上げる予定です。今後検討できるもう1つの興味深い側面は、GPがカーネル合成を可能にすることです。カーネル合成では、線形カーネルとRBFカーネルのスタッキングなどの複数のカーネルを使用して、データセット間のより複雑な関係をモデル化できます。これには、短期的な価格変動パターンと長期的な傾向などの組み合わせが含まれる可能性があり、モデルは最適なポイントでポジションから抜け出すと同時に、証券が持つ可能性のある潜在的な長期的な変動も活用できます。

GPには、ノイズ処理と削減、体制変更への適応など、他にもさまざまな利点と用途があります。しかし、取引者としては、これらの利点を活用したいので、非常に基本的な線形カーネルを見てみましょう。

線形カーネル

線形カーネルの主な用途は、ガウス過程においてデータセット間の単純な線形関係をマッピングすることです。たとえば、非常に単純なデータセットのペアとして、中国から米国へのコンテナの輸送コストと海運ETF BOATの価格について考えてみましょう。通常の状況では、輸送コストが高いことは海運会社の価格決定力を反映し、これが収益に反映され、株価の上昇につながることが期待されます。このシナリオでは、海運会社を長期的に購入する、または単にETFを購入することを検討する取引者は、線形カーネルを使用して、予想される株価と現在の輸送コストをモデル化することに関心があるでしょう。

これは比較的単純で計算コストも低く、すべてのカーネルの中で最も少ない計算リソースを必要とします。また、式には1つの定数パラメータcのみが必要です。この式は以下のように示されます。

ここで

• xとx′は入力ベクトル
• x^⊤x′ は転置ベクトルxとx′の内積
• cは定数

このパラメータcのみが必要なため、大規模なデータセットでも高速かつ非常に効率的です。この定数の役割は主に4つあります。まず、バイアス調整に役立ちます。つまり、データセットやプロットが原点を通過しない場合、この定数がオフセットを提供し、ハイパープレーンをシフトさせてカーネルが基礎モデルをより適切に表現できるようにします。この定数がない場合、カーネルはすべてのデータポイントが原点を中心としていると仮定します。この定数自体は最適化されませんが、事前設定されたクロス検証手順で調整可能です。

第二に、この定数は、2つのデータセットクラス間の分離をよりカスタマイズするために、このマージンギャップを制御します。これは、カーネルをサポートベクターマシンで使用する場合や、簡単に線形に分離できない大規模なデータセットがある場合に特に重要です。第三に、この定数は、特定のデータセットに存在する可能性のある非線形同質性を有効にします。この定数がない場合、すべての入力が係数でスケーリングされると、カーネルの出力も同じ係数でスケーリングされます。一部のデータセットはこの特性を示しますが、すべてではありません。したがって、このc定数を追加すると、固有のバイアスが追加され、モデルが自動的に線形であると仮定しなくなります。

最後に、非常に小さな値になり、カーネル行列を歪める可能性のあるドット積に数値的安定性を与えるとされています。入力ベクトルの値が非常に小さい場合、定数のないドット積も非常に小さくなり、最適化プロセスに影響を及ぼします。したがって、定数は、より優れた最適化のための安定性を提供します。

線形カーネルは、観測データを超えた傾向を外挿するため、外挿と傾向予測に応用されます。したがって、特に資産の線形増価率が時間とともに問題になるような場合には、線形カーネルが役立ちます。また、ドット積による特徴の重み付けにより、線形カーネルモデルの解釈可能性が向上します。解釈可能性は、入力データのベクトルがあり、このベクトル内の各入力データポイントの相対的な重要性や意義を知る必要がある場合に便利です。たとえば、住宅価格の予測に使用するカーネルがあるとします。このカーネルには、住宅の面積（平方フィート）、寝室数、地域の収入中央値、建築年を含む4つのサイズの入力データベクトルが含まれます。カーネルからの予測価格は以下の式で提供されます。

ここで

• bはベクトルのドット積に加える定数で、その役割はすでに上で強調したとおりである（cと呼ぶ）
• w1からw4は、訓練によって最適化される重み
• x1からx4は、前述したデータ入力

訓練後、w1からw4の値を取得し、この単純な線形カーネル設定では、重みが大きいほど、特徴またはデータポイントが物件の次の価格にとって重要になります。たとえば、重みw4が最小の場合、x4（物件が購入された年）は次の価格にとって最も重要でないことを意味します。ただし、この設定での線形カーネルの使用は、ガウス過程回帰での線形カーネルの使用です。つまり、特徴の重要性を推測する必要がある場合、上記のドット積の出力はスカラーですが、アプリケーションでは行列であるため、上記で示したほど簡単ではありません。しかし、入力データの相対的な重要性を把握するための代替案として、automatic relevance determination（英語）（自動関連性判定）、感度分析（選択した入力を調整し、その影響を予測で観察する）、および周辺尤度とハイパーパラメータ（バッチ正規化のようなハイパーパラメータの大きさによって入力データの相対的な重要性を推測できる）が含まれます。

ガウス過程回帰内で使用する線形カーネルをMQL5で以下のように実装します。

//+------------------------------------------------------------------+
// Linear Kernel Function
//+------------------------------------------------------------------+
matrix CSignalGauss::Linear_Kernel(vector &Rows, vector &Cols)
{  matrix _linear, _c;
   _linear.Init(Rows.Size(), Cols.Size());
   _c.Init(Rows.Size(), Cols.Size());
   for(int i = 0; i < int(Rows.Size()); i++)
   {  for(int ii = 0; ii < int(Cols.Size()); ii++)
      {  _linear[i][ii] = Rows[i] * Cols[ii];
      }
   }
   _c.Fill(m_constant);
   _linear += _c;
   return(_linear);
}

ここでの入力は、式で示されているように2つのベクトルであり、1つには「Rows」というラベルが付けられ、これはドット積に適用される前にこのベクトルの転置を意味します。線形カーネルは、上記の利点に加えてセットアップとテストが最も簡単なため、他のより複雑なカーネルやモデルを比較するための基準として機能します。線形カーネルから始めることで、他のカーネルの追加の複雑さが正当化されるかどうかに応じて、徐々にスケールアップできます。これは、カーネルが複雑になるにつれて計算コストも増加するため、特に大規模なデータセットとカーネルを処理する場合に重要です。ただし、線形カーネルは長期的な依存関係をキャプチャし、より複雑な関係を定義するために他のカーネルと組み合わせることも可能で、比較するデータセットに強い線形関係がある場合に正規化の形式として機能します。

Matérnカーネル

Matérnカーネルは、調整可能な滑らかさとデータ依存性を捉える能力のため、ガウス過程で使用される一般的な共分散関数でもあります。その滑らかさは、入力パラメータν（発音は「ニョー」）によって制御されます。このパラメータは、その滑らかさを調整できるため、νが½のときはMatérnカーネルをギザギザの指数カーネルとしてマッピングでき、このパラメータが∞に近づくときはラジアルベース関数カーネルとしてマッピングできます。その式は、第一原理から次のように与えられます。

ここで

• ∥x-x′∥は2点間のユークリッド距離
• νは平滑性を制御するパラメータ
• lは長さスケールのパラメータ（RBFカーネルと同様）
• (ν)はガンマ関数
• Kνは第2種の修正Bessel関数

ガンマ関数とベッセル関数は少々難解なのでここでは取り上げませんが、ここではνを³/2としています。これにより、カーネルは指数カーネルとラジアルRBFカーネルのほぼ中間になります。こうすると、Matérnカーネルの式は次のように簡略化されます。

ここで

• 表現は、上記で共有した最初の式と同様

以下は特殊なケースです。

• ν=¹/2の場合、Matérnカーネルは指数カーネルとなる
• ν→∞の場合はRBFカーネルとなる

このカーネルの滑らかさはνパラメータに非常に敏感で、通常¹/2、³/2、⁵/2のいずれかが割り当てられます。これらのパラメータ値はそれぞれ、滑らかさの度合いが異なることを意味し、値が大きいほど滑らかさが増します。

vが¹/2場合、カーネルは前述の指数カーネルと同等であり、急激な変化や不連続が一般的なデータセットのモデリングに適しています。トレーダーの観点から見ると、これは通常、非常に変動の激しい証券または外国為替ペアを指します。このカーネル設定は、ギザギザのプロセスを前提としているため、結果が滑らかではなく、即時の変化に敏感であると言えます。νが³/ 2の場合（ウィザードで組み立てられたEAをテストする際にこの記事で採用している設定）、その滑らかさは中程度と評価されることがよくあります。これは、中程度の変動データと中程度の傾向のあるデータセットの両方を処理できるという点で妥協点です。この種の設定では、カーネルは時系列の転換点や市場の変動点の判定に適していると言えます。⁵/ ²以上の設定では、特にレートが問題となる場合、カーネルは傾向のある環境により適しています。

したがって、ノイズの多いデータや、ジャンプや不連続があるデータセットには、より小さいν値の方が適していますが、より緩やかで滑らかな変化があるデータセットには、より高いν値の方が適しています。補足として、微分可能性、つまりカーネル関数を微分できる回数は、νパラメータとともに増加します。これは、より高いνパラメータ値を持つ計算リソースと相関し、より多くの計算を使用します。MQL5では、次のようにMatérnカーネルを実装します。

//+------------------------------------------------------------------+
// Matern Kernel Function
//+------------------------------------------------------------------+
matrix CSignalGauss::Matern_Kernel(vector &Rows,vector &Cols)
{  matrix _matern;
   _matern.Init(Rows.Size(), Cols.Size());
   for(int i = 0; i < int(Rows.Size()); i++)
   {  for(int ii = 0; ii < int(Cols.Size()); ii++)
      {  _matern[i][ii] = (1.0 + (sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next)) * exp(-1.0 * sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next);
      }
   }
   return(_matern);
}

したがって、線形カーネルと比較すると、Matérnカーネルはより柔軟で、複雑で非線形なデータ関係を捉えるのに適しています。多くの現実世界の現象やデータをモデル化する場合、上で見たように、νパラメータをわずかに調整するだけで、傾向のあるデータセットだけでなく、不安定で不連続なデータも処理できるため、線形カーネルよりも明らかに有利です。

シグナルクラス

シグナル クラス内の2つの実装オプションとして2つのカーネルをまとめるカスタムシグナルクラスを作成します。出力取得関数も、EAの入力からカーネル選択を選択できるように再コーディングされています。新しい関数は次のとおりです。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalGauss::GetOutput(double BasisMean, vector &Output)
{  

   ...

   matrix _k_s;
   matrix _k_ss;
   _k_s.Init(_next_time.Size(), _past_time.Size());
   _k_ss.Init(_next_time.Size(), _next_time.Size());
   if(m_kernel == KERNEL_LINEAR)
   {  _k_s = Linear_Kernel(_next_time, _past_time);
      _k_ss = Linear_Kernel(_next_time, _next_time);
   }
   else if(m_kernel == KERNEL_MATERN)
   {  _k_s = Matern_Kernel(_next_time, _past_time);
      _k_ss = Matern_Kernel(_next_time, _next_time);
   }

   ...

}

適切なカーネルが選択されると、次の価格変更を補間する手順は、以前の記事で説明したものと同じです 。売買条件の処理にも大きな違いはありません。完全性を保つためにそのコードをここで共有します。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalGauss::LongCondition(void)
{  int result = 0;
   vector _o;
   GetOutput(0.0, _o);
   if(_o[_o.Size()-1] > _o[0])
   {  result = int(round(100.0 * ((_o[_o.Size()-1] - _o[0])/(_o.Max() - _o.Min()))));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalGauss::ShortCondition(void)
{  int result = 0;
   vector _o;
   GetOutput(0.0, _o);
   if(_o[_o.Size()-1] < _o[0])
   {  result = int(round(100.0 * ((_o[0] - _o[_o.Size()-1])/(_o.Max() - _o.Min()))));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}

リンクされた記事の条件は、予測価格の変化がプラスになるかマイナスになるかに基づいています。これらの変化は、すべてのカスタムシグナルクラスインスタンスで期待されるように、0～100の整数範囲に正規化されます。MQL5ウィザードを使用してこのシグナルファイルをEAに組み立てる方法については、初心者向けに、こちらとこちらの別の記事で説明しています。

ストラテジーテスターレポート

GBPJPYペア、2023年の日次時間枠で線形カーネルとMatérnカーネルを使用していくつかの最適化を実行します。それぞれの結果は、エキスパートアドバイザーの使いやすさを示すだけであり、将来のパフォーマンスを示唆するものではありません。以下に示します。

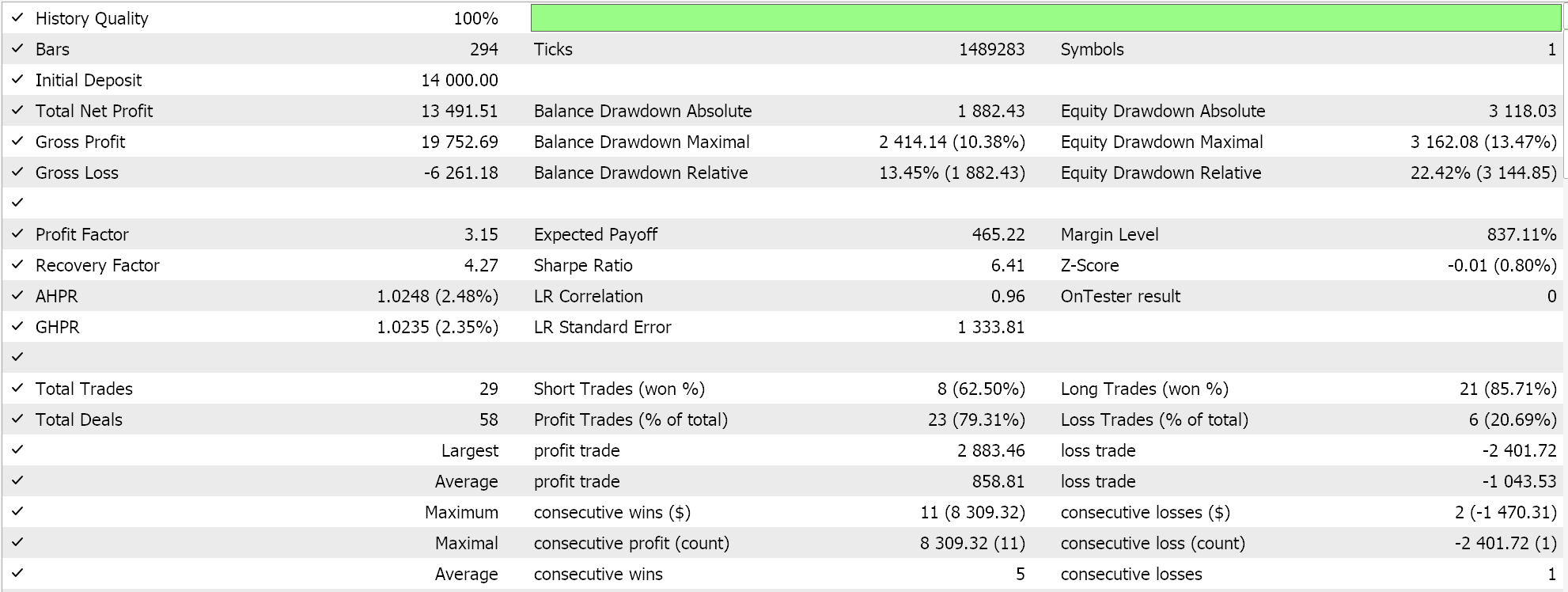
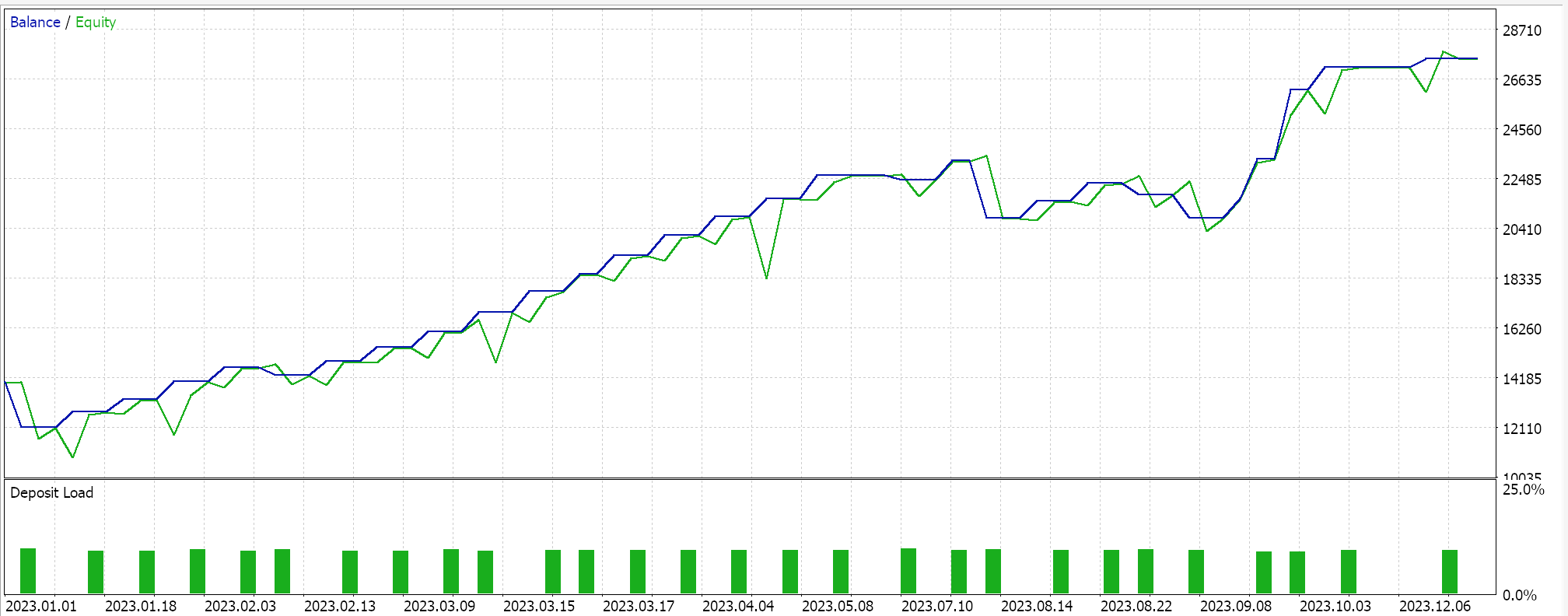
そして、Matérnカーネルの結果は以下の通りです。

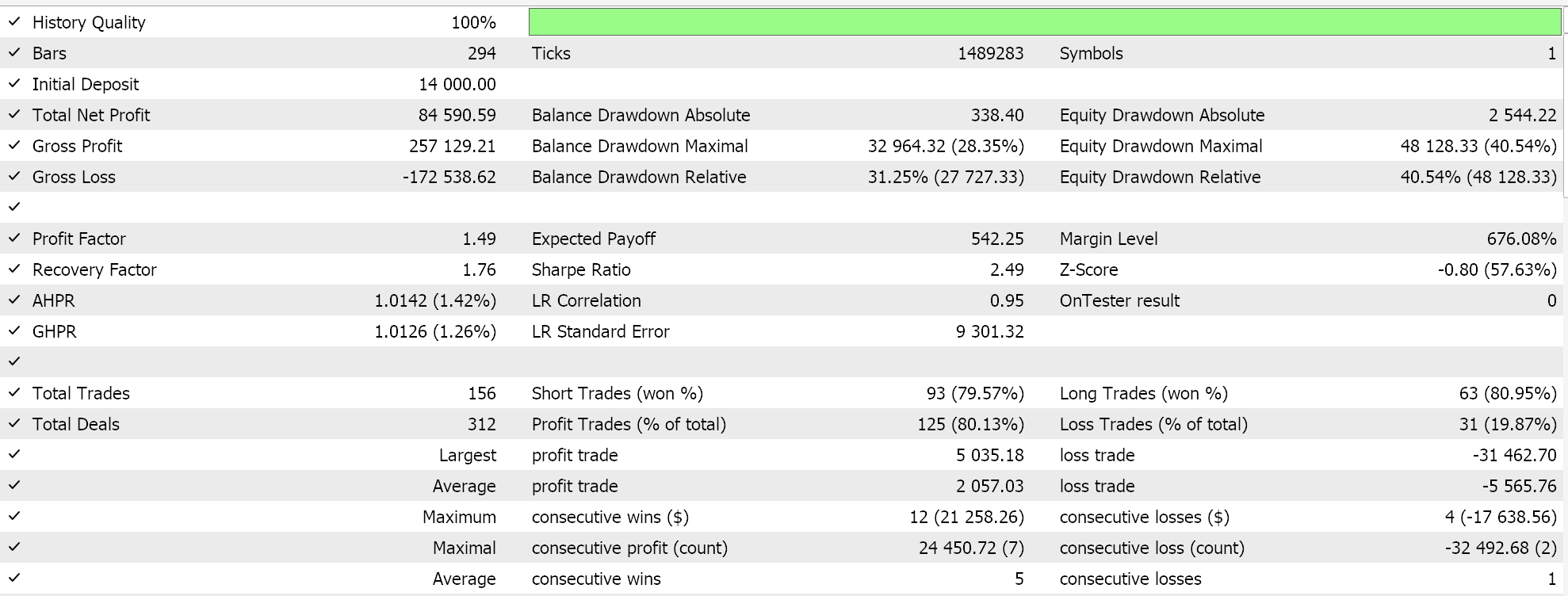
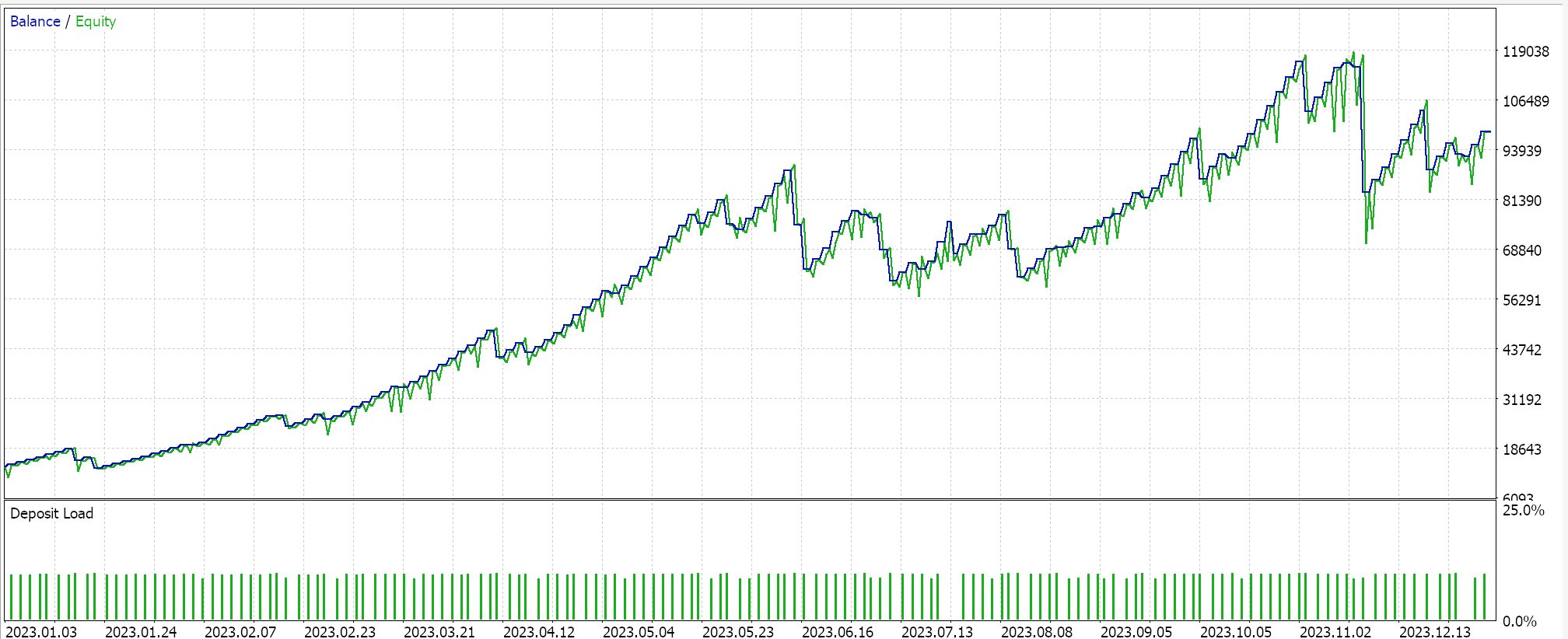
両方のカーネルの代替実装は、カスタム資金管理クラスを使用することもできます。これもシグナルと同様にMQL5ウィザードで組み立てることができますが、違いは資金管理のカスタムインスタンスが1つだけ選択される点です。シグナルクラスでおこなったようにガウス過程回帰を使用するには、カスタムシグナルクラスとカスタム資金管理クラスの両方で参照される共通のアンカー クラスが理想的です。これにより、2つのカスタムクラスで非常によく似たタスクをおこなう同じ関数のコーディングの重複が最小限に抑えられます。

しかし、資金管理クラスでは、ガウス過程カーネルに供給されるデータのタイプに若干の変更があります。カスタムシグナルクラスの入力データセットとして終値の変化があったのに対し、この資金管理クラスでは、カーネルへの入力としてATR指標の変化があります。カーネルの出力は、ATRの次の変化になるように訓練されます。よく知らない人のために説明すると、このカスタムクラスは、EAが損失を被った場合にポジションサイズを減らすように構築された、一般的な資金サイズ最適化クラスからの適応でもあります。ロットサイズの削減率は、被った損失の連続に比例します。このクラスを採用し、ロットの削減が行われるタイミングを制御するいくつかの変更をおこないます。

私たちの変更により、EAが損失を被り、予測値全体でATRが上昇する予測がある場合にのみロットを減らします。これらの予測値の数は、このシリーズでガウス過程回帰を紹介した既にリンクされている記事で説明されているように、m_nextパラメータによって設定されます。これらの変更と、ポジションサイズを最適化するための元のコードのほとんどを以下に共有します。

//+------------------------------------------------------------------+
//| Optimizing lot size for open.                                    |
//+------------------------------------------------------------------+
double CMoneyGAUSS::Optimize(int Type, double lots)
{  double lot = lots;
//--- calculate number of losses orders without a break
   if(m_decrease_factor > 0)
   {  //--- select history for access
      HistorySelect(0, TimeCurrent());
      //---
      int       orders = HistoryDealsTotal(); // total history deals
      int       losses = 0;                  // number of consequent losing orders
      //--
      int      size = 0;
      matrix series;
      series.Init(fmin(m_series_size, orders), 2);
      series.Fill(0.0);
      //--
      CDealInfo deal;
      //---
      for(int i = orders - 1; i >= 0; i--)
      {  deal.Ticket(HistoryDealGetTicket(i));
         if(deal.Ticket() == 0)
         {  Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history");
            break;
         }
         //--- check symbol
         if(deal.Symbol() != m_symbol.Name())
            continue;
         //--- check profit
         double profit = deal.Profit();
         //--
         series[size][0] = profit;
         size++;
         //--
         if(size >= m_series_size)
            break;
         if(profit < 0.0)
            losses++;
      }
      //--
      double _cond = 0.0;
      //--
      vector _o;
      GetOutput(0.0, _o);
      //---
      //decrease lots on rising ATR
      if(_o[_o.Size()-1] > _o[0])
         lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2);
   }
//--- normalize and check limits
   double stepvol = m_symbol.LotsStep();
   lot = stepvol * NormalizeDouble(lot / stepvol, 0);
//---
   double minvol = m_symbol.LotsMin();
   if(lot < minvol)
      lot = minvol;
//---
   double maxvol = m_symbol.LotsMax();
   if(lot > maxvol)
      lot = maxvol;
//---
   return(lot);
}

上記で示したように、ガウス過程カーネルを利用するカスタムトレーリングクラスを作成する際にも、同様のアプローチを取ることができます。ベク取るおよび行列データ型によって提供される簡単な価格アクセスに加えて、さまざまな指標から選択することも可能です。

結論

結論として、金融時系列で予測をおこなう際にこの形式の回帰で使用できる別のカーネルセットを検討することで、ガウス過程回帰の調査を続けました。線形カーネルとMatérnカーネルは、適しているデータセットの種類だけでなく、柔軟性においてもほぼ正反対です。線形カーネルは特定の種類のデータセットしか処理できませんが、特に研究開始時にデータセットサンプルのサイズが小さい場合は、線形カーネルを使用してモデリングを開始するのが実用的であることがよくあります。時間の経過とともに、データセットサンプルが増加し、データがより複雑になったり、ノイズが増えたりすると、Matérnカーネルのようなより堅牢なカーネルを使用して、ノイズの多いデータやギャップや中断だけでなく、非常に滑らかなデータセットも処理できます。これは、主要な入力パラメータvを調整できるため、データセットによって提示される課題に応じて異なる役割を担うことができ、ほとんどのデータ環境に適していると言えるでしょう。