MQL5とPythonで自己最適化エキスパートアドバイザーを構築する（第2回）：ディープニューラルネットワークのチューニング

MetaTrader 5 — 例 | 10 10月 2024, 08:46

はじめに

私たちのコミュニティのメンバーは、AIを取引戦略に取り入れることに強い関心を持っています。しかし、そのためには、特定の市場に合わせてAIモデルを適切にチューニングする必要があります。AIモデルには、パフォーマンスに大きく影響を与える調整可能なパラメータがいくつか存在し、ある市場に最適な設定が、別の市場ではうまく機能しない場合もあります。この記事では、最適化アルゴリズム、特にNelder-Meadアルゴリズムを使用して、AIモデルをカスタマイズし、デフォルト設定以上のパフォーマンスを引き出す方法を解説します。また、このアルゴリズムを活用して、MetaTrader 5端末からのデータを基にディープニューラルネットワークを微調整し、エキスパートアドバイザー(EA)で使用するための最適化済みモデルをONNX形式でエクスポートする手順も紹介します。これらの概念に馴染みのない方にも、記事内で詳しく説明しています。

Nelder-Mead最適化アルゴリズム

Nelder-Meadアルゴリズムは、ノイズが多く、微分不可能で、非線形な多峰性の最適化問題に頻繁に使用されます。このアルゴリズムは、発明者のジョン・ネルダーとロジャー・ミードにちなんで命名され、1965年の論文「A Simplex Method for Function Minimization」で紹介されました。一変量および多変量の最適化問題に対応できます。

Nelder-Meadアルゴリズムは、導関数に依存せず、パターン探索型の最適化アルゴリズムです。ユーザーが初期の出発点を指定する必要がありますが、選んだ開始点によってはアルゴリズムが局所最適解に陥る可能性があります。そのため、大域的な最適解を見つけやすくするために、開始点を変えて複数回最適化を実行することが効果的です。

このアルゴリズムは「単体」と呼ばれる幾何学的形状を用いて動作します。単体は、各入力変数に対応する頂点と、さらに1つの頂点を持つ構造です。アルゴリズムは単体の頂点を評価し、その評価に基づいてシンプルなルールで点を移動させていきます。最大反復回数に達するか、評価値の変化が最小限にとどまった場合など、一定の停止条件に従って最適化は終了します。改善が見られない場合や、指定した回数を超えると最適化プロセスは停止します。

ロジャーミード

図1：ロジャー・ミード氏

ジョンネルダー

図2：ジョン・ネルダー氏

初めのステップ

MetaTrader 5端末から必要なデータを取得することから始めます。まず、MetaTrader 5端末を開き、コンテキストメニューの銘柄アイコンをクリックします。そこからバーを選択し、使用したい銘柄を検索します。データをリクエストしたら、エクスポートをクリックするだけで、データがCSV形式で利用できるようになります。

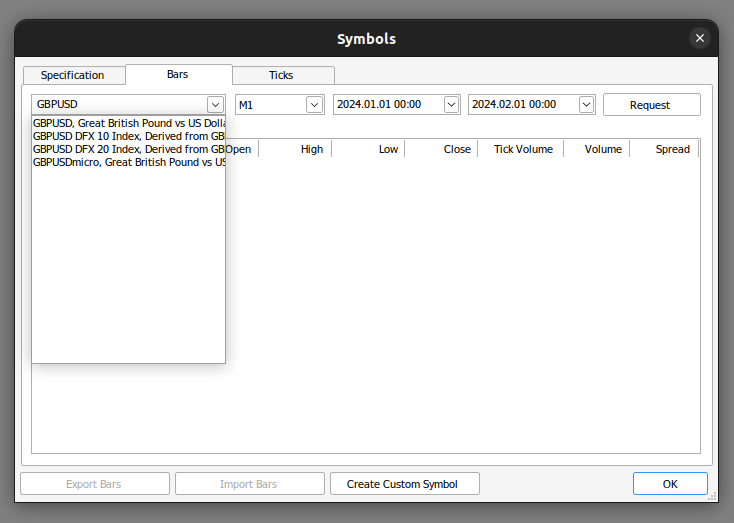
図3：必要なデータを検索

データの準備ができたので、必要なライブラリをインポートすることから始めましょう。

#import libraries we need
import pandas as pd
import numpy as np
from numpy.random import randn,rand
import seaborn as sns

次に、用意したデータを読み込みます。

#Read in our market data
brent = pd.read_csv("/home/volatily/market_data/Market Data UK Brent Oil.csv", sep="\t")

データにラベルを付けます。

#Preparing to label the data
look_ahead = 20

#Defining the target
brent["Target"] = brent["Close"].shift(-look_ahead)

#Drop missing values
brent.dropna(inplace=True)

最適化に必要なライブラリをインポートします。

#In this article we will cover some techniques for hyper-parameter tuning 
from scipy.optimize import minimize
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import root_mean_squared_error
import time

ここで時系列交差検証オブジェクトを作成します。

#Define the time series split parameters
splits = 5
gap = look_ahead

#Create the time series split object
tscv = TimeSeriesSplit(n_splits=splits,gap=gap)

#Create a dataframe to store our accuracy 
current_error_rate = pd.DataFrame(index = np.arange(0,splits),columns=["Current Error"])

モデルの予測変数とターゲットを定義します。

#Define the predictors and the target
predictors = ["Open","High","Low","Close"]
target = "Target"

ここで、最小化を目指す関数、すなわちモデルの交差検証誤差を定義します。これはデモンストレーションのためのものです。理想的には、データセットを半分に分割し、片方で最適化をおこない、もう片方で精度を測定します。しかし、今回のデモでは、同じデータセットを使ってモデルを最適化し、その精度を測定します。

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    model = MLPRegressor(hidden_layer_sizes=(5,2),alpha=x[0],early_stopping=True,shuffle=False,learning_rate_init=x[1],tol=x[2])
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(brent)):
        #The data
        X_train = brent.loc[train[0]:train[-1],predictors]
        y_train = brent.loc[train[0]:train[-1],target]
        X_test  = brent.loc[test[0]:test[-1],predictors]
        y_test  = brent.loc[test[0]:test[-1],target]
        #Train the model
        model.fit(X_train,y_train)
        #Measure the RMSE
        current_error_rate.iloc[i,0] = root_mean_squared_error(y_test,model.predict(X_test))
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

Nelder-Meadアルゴリズムが最初の開始点を必要とすることを思い出してください。良い出発点を見つけるために、問題のパラメータを線で検索します。パラメータを0.1、次に0.01と設定し、forループを使って精度を測定します。これによって、アルゴリズムの出発点を特定することができます。

#Let us measure how much time this takes.
start = time.time()

#Create a dataframe to measure the error rates
starting_point_error = pd.DataFrame(index=np.arange(0,21),columns=["Average CV RMSE"])
starting_point_error["Iteration"] = np.arange(0,21)

#Let us first find a good starting point for our optimization algorithm
for i in np.arange(0,21):
    #Set a new starting point
    new_starting_point = (10.0 ** -i)
    #Store error rates
    starting_point_error.iloc[i,0] = objective([new_starting_point,new_starting_point,new_starting_point]) 

#Record the time stamp at the end
stop = time.time()

#Report the amount of time taken
print(f"Completed in {stop - start} seconds")

312.29402351379395秒で完了です。

では、誤差レベルを見てみましょう。

平均CV RMSE	反復
0.91546	0
0.267167	1
14.846035	2
15.763264	3
56.820397	4
75.202923	5
72.562681	6
64.33746	7
88.980977	8
83.791834	9
82.871215	10
88.031151	11
65.532539	12
78.177191	13
85.063947	14
88.631589	15
74.369735	16
86.133656	17
90.482654	18
102.803612	19
74.636781	20

見ての通り、反復0から2の間に最適な領域を通過したようです。この後、誤差が増加し続けました。同じ情報を視覚的に観察することができます。

sns.lineplot(data=starting_point_error,x="Iteration",y="Average CV RMSE")

誤差率

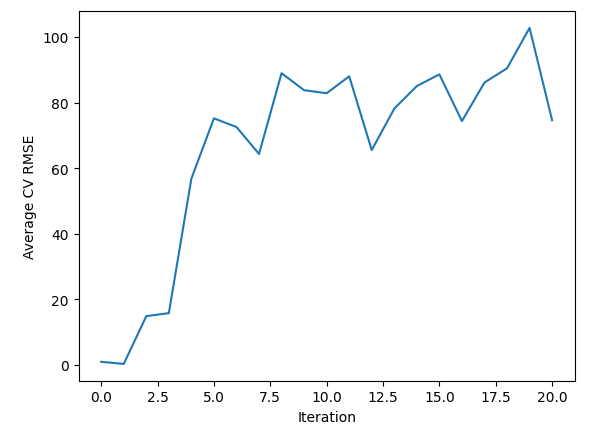
図4：ライン検索結果の可視化

良い出発点が何であるか見当がついたので、最適と思われる範囲内のランダムな点を与える関数を定義してみましょう。

pt = abs(((10 ** -1) + rand(3) * ((10 ** 0) - (10 ** -1))))
pt

array([0.75747551, 0.34066536, 0.26214705])

ニューラルネットワークの3つの異なるパラメータを最適化しているため、3つのランダムな値の配列をフェッチしていることに注意してください。それでは、ハイパーパラメータのチューニングをおこないます。

start = time.time()
result = minimize(objective,pt,method="nelder-mead")
stop = time.time()
print(f"Task completed in {stop - start} seconds")

1332.9911317825317秒でタスク完了です。

最適化の結果を解釈してみましょう。

result

message:Maximum number of function evaluations has been exceeded.
       success:false
        status:1
           fun:0.12022686955703668
             x: [ 7.575e-01 3.577e-01 2.621e-01]
           nit:225
          nfev:600
final_simplex: (array([[ 7.575e-01, 3.577e-01, 2.621e-01],
                       [ 7.575e-01, 3.577e-01, 2.621e-01],
                       [ 7.575e-01, 3.577e-01, 2.621e-01],
                       [ 7.575e-01, 3.577e-01, 2.621e-01]]), array([ 1.202e-01, 2.393e-01, 2.625e-01, 8.978e-01])

まず、上部に表示されるユーザーフレンドリーなメッセージをご覧ください。このメッセージは、アルゴリズムが関数の最大評価数を超えたことを示します。最適化が停止するシナリオについて、先に指定した条件を思い出してください。許容反復回数を増やしてみることはできますが、パフォーマンスの向上は保証されません。

「fun」というキーが見えますが、これはアルゴリズムが関数から得た最適出力を示しています。それに続くのが「x」というキーで、最適な出力をもたらしたxの値を示しています。

また、「nit」キーを観察することで、関数が実行した反復回数を知ることができます。最後に、「nfev」キーは、アルゴリズムが出力を評価するために目的関数を呼び出した回数を示します。目的関数が5倍の相互検証をおこない、平均誤差率を返したことを思い出してください。つまり、この関数を1回呼び出すたびに、ニューラルネットワークを5回フィッティングすることになります。したがって、600回の関数評価は、ニューラルネットワークを3000回適合させたことを意味します。

では、デフォルトのモデルと私たちが作ったカスタマイズモデルを比較してみましょう。

#Let us compare our customised model and the defualt model
custom_model = MLPRegressor(hidden_layer_sizes=(5,2),alpha=result.x[0],early_stopping=True,shuffle=False,learning_rate_init=result.x[1],tol=result.x[2])

#Default model
default_model = MLPRegressor(hidden_layer_sizes=(5,2))

時系列分割オブジェクトを用意します。

#Define the time series split parameters
splits = 10
gap = look_ahead

#Create the time series split object
tscv = TimeSeriesSplit(n_splits=splits,gap=gap)

#Create a dataframe to store our accuracy 
model_error_rate = pd.DataFrame(index = np.arange(0,splits),columns=["Default Model","Custom Model"])

各モデルの相互検証をおこないます。

#Now we will cross validate the model
for i,(train,test) in enumerate(tscv.split(brent)):
    #The data
    X_train = brent.loc[train[0]:train[-1],predictors]
    y_train = brent.loc[train[0]:train[-1],target]
    X_test  = brent.loc[test[0]:test[-1],predictors]
    y_test  = brent.loc[test[0]:test[-1],target]
    #Our model
    model = MLPRegressor(hidden_layer_sizes=(5,2),alpha=result.x[0],early_stopping=True,shuffle=False,learning_rate_init=result.x[1],tol=result.x[2])
    #Train the model
    model.fit(X_train,y_train)
    #Measure the RMSE
    model_error_rate.iloc[i,1] = root_mean_squared_error(y_test,model.predict(X_test))

誤差メトリクスを見てみましょう。

model_error_rate

デフォルトモデル	カスタマイズモデル
0.153904	0.550214
0.113818	0.501043
82.188345	0.52897
0.114108	0.117466
0.114718	0.112892
77.508403	0.258558
0.109191	0.304262
0.142143	0.363774
0.163161	0.153202
0.120068	2.20102

また、結果を可視化してみましょう。

model_error_rate["Default Model"].plot(legend=True)
model_error_rate["Custom Model"].plot(legend=True)

モデルのパフォーマンスを可視化する

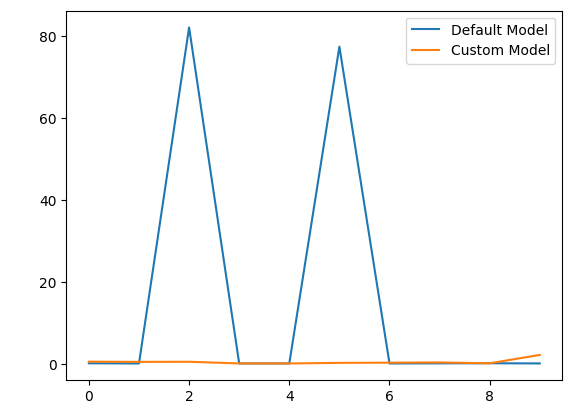
図5：カスタマイズしたモデルのパフォーマンスを可視化する

観察できるように、カスタマイズモデルはデフォルトモデルを上回りました。しかし、モデルの訓練と精度の評価に別々のデータセットを使っていれば、今回のテストはもっと説得力のあるものになったでしょう。両方の目的で同じデータセットを使うのは理想的な手順ではありません。

次に、ディープニューラルネットワークをONNX表現に変換する準備をします。ONNXはOpen Neural Network Exchangeの略で、標準化されたフォーマットであり、これに準拠したフレームワークで訓練されたAIモデルをさまざまなプログラムで使用できるようにします。例えば、ONNXを使えば、PythonでAIモデルを訓練し、それをMQL5やJavaプログラム（Java APIがONNXをサポートしている場合）で使用することができます。

まず、必要なライブラリをインポートします。

#Now we will prepare to export our neural network into ONNX format
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn
import onnxruntime as ort
import netron

このモデルの入力形状を定義してみましょう。このモデルは4つの入力を取ることを覚えておいてください。

#Define the input types
initial_type = [("float_input",FloatTensorType([1,4]))]

カスタマイズされたモデルにフィットします。

#Fit our custom model
custom_model.fit(brent.loc[:,["Open","High","Low","Close"]],brent.loc[:,"Target"])

skl2onnxライブラリのおかげで、ディープニューラルネットワークのONNX表現を作るのは簡単です。

#Create the onnx represantation
onnx = convert_sklearn(custom_model,initial_types=initial_type,target_opset=12)

ONNXファイルの名前を定義します。

#The name of our ONNX file
onnx_filename = "Brent_M1.onnx"

次に、ONNXファイルを書き出します。

#Write out the ONNX file
with open(onnx_filename,"wb") as f:
    f.write(onnx.SerializeToString())

ONNXモデルのパラメータを調べてみます。

#Now let us inspect our ONNX model
onnx_session = ort.InferenceSession(onnx_filename)
input_name   = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

入力形状を見てみましょう。

for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

1. Name: float_input, Data Type: tensor(float), Shape: [1, 4]

モデルの出力形状を見てみましょう。

for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

1. Name: variable, Data Type: tensor(float), Shape: [1, 1]

これでnetronを使ってモデルを視覚的に見ることができます。これらのステップを踏むことで、ONNXの入力と出力の形状が私たちの期待に合致していることを確認することができます。

#We can also inspect our model visually using netron.
netron.start(onnx_filename)

ネトロン映像

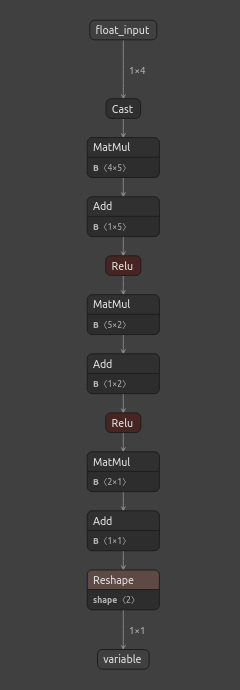
図6：ニューラルネットワークのONNX表現

ONNXファイルメタ情報

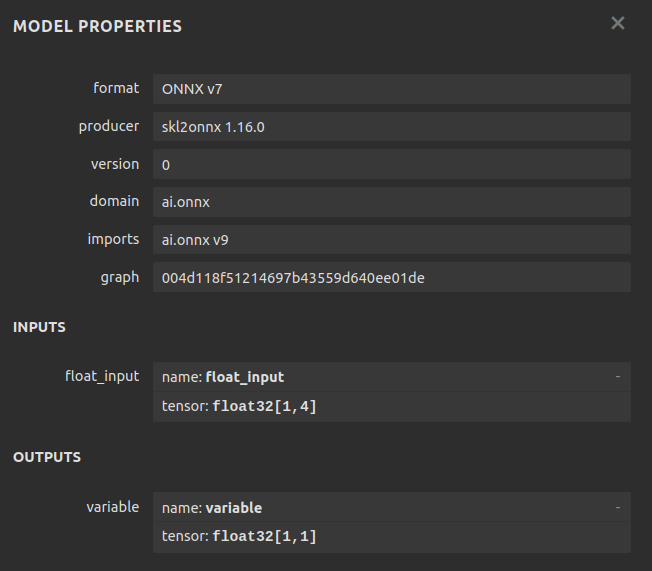
図7：ONNXモデルのメタ詳細

NetronはオープンソースのPythonライブラリで、ONNXモデルを視覚的に検査し、パラメータをチェックし、メタデータをレビューすることができます。MetaTrader 5でONNXモデルを使用する方法についてもっと知りたい方には、よく書かれた記事がたくさんあります。このテーマで私が好きな著者の一人にOmegaがいます。

MQL5での実装

ONNXモデルの設定が完了したら、MQL5でEAの構築を開始します。

MQL5アプリケーションの概略図

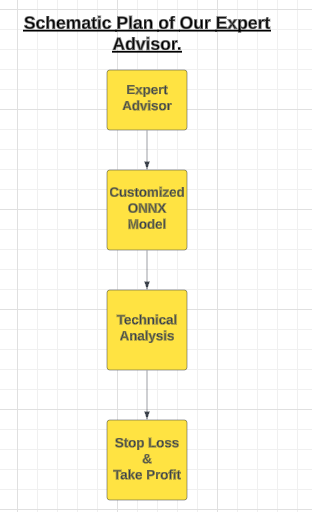
図8：EAの概略図

私たちのEAは、カスタマイズされたONNXモデルを使用してエントリシグナルを生成します。しかし、優れたトレーダーは皆、受け取ったエントリシグナルをすべて実行するわけではなく、慎重に行動します。この規律をEAに植え付けるために、ポジションを建てる前にテクニカル指標からの確認を待つようにプログラムします。

これらのテクニカル指標は、エントリのタイミングを効果的に計るのに役立ちます。ポジションが建てられると、ユーザー定義のストップロスレベルがそのポジションを決済します。最初のステップは、アプリケーションのリソースとしてONNXモデルを指定することです。

//+------------------------------------------------------------------+
//|                                   Custom Deep Neural Network.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load the ONNX model                                              |
//+------------------------------------------------------------------+
#resource "\\Files\\Brent_M1.onnx" as const uchar ModelBuffer[];

次に、ポジション管理に不可欠な取引ライブラリをロードします。

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

次に、プログラムのグローバル変数を作成しましょう。

//+------------------------------------------------------------------+
//| Gloabal variables                                                |
//+------------------------------------------------------------------+
long model; //The handler for our ONNX model
vector forecast = vector::Zeros(1); //Our model's forecast

const int states = 3; //The total number of states the system can be in
vector state = vector::Zeros(states); //The state of our system

int mfi_handler,wpr_handler; //Handlers for our technical indicators
vector mfi_reading,wpr_reading; //The values of our indicators will be kept in vectors

double minimum_volume, trading_volume; //Smallest lot size allowed & our calculated lotsize
double ask_price, bid_price; //Market rates

EAの動作を変更できるユーザー入力を定義してみましょう。

//+------------------------------------------------------------------+
//| Inputs                                                           |
//+------------------------------------------------------------------+
input int mfi_period = 20; //Money Flow Index Period
input int wpr_period = 30; //Williams Percent Range Period

input int lot_multiple = 20; //How big should our lot sizes be?
input double sl_width = 2; //How tight should the stop loss be?

input double max_profit = 10; //Close the position when this profit level is reached.
input double max_loss = 10; //Close the position when this loss level is reached.

私たちのアプリケーションは、特定のルーチンを実行するための補助関数を必要とします。まず、アプリケーションの状態を管理する関数を定義します。状態0はポジションがないことを意味し、状態1と2はそれぞれ買いポジションまたは売りポジションを示します。

現在の状態に応じて、アプリケーションは異なる関数にアクセスできます。

//+------------------------------------------------------------------+
//| This function is responsible for updating the system state       |
//+------------------------------------------------------------------+
void update_state(int index)
  {
//--- Reset the system state
   state = vector::Zeros(states);
//--- Now update the current state
   state[index] = 1;
  }

次に、アプリケーションの起動時にユーザーの入力を検証する関数が必要です。例えば、この関数はすべてのテクニカル指標期間が0より大きいことを保証します。

//+------------------------------------------------------------------+
//| This function will ensure that user inputs are valid             |
//+------------------------------------------------------------------+
bool valid_inputs(void)
  {
//--- Let us validate the inputs the user passed
   return((mfi_period > 0)&&(wpr_period > 0) && (max_profit >= 0) && (max_loss >= 0) && (lot_multiple >= 0) && (sl_width >= 0));
  }

私たちのEAは、利益水準がユーザーの指定した入力値を満たしているかどうかを継続的にチェックします。例えば、ユーザーが最大利益目標を1ドルに設定した場合、ポジションは利益確定レベルに達していなくても、利益が1ドルに達すれば自動的に決済されます。同じロジックがストップロスにも適用されます。ストップロスレベルであれ最大損失レベルであれ、どちらの閾値に最初にヒットしたかに基づいてポジションは決済されます。この機能は、許容できるリスクレベルを柔軟に定義できるように設計されています。

//+------------------------------------------------------------------+
//| This function will check our profit levels                       |
//+------------------------------------------------------------------+
void check_profit_level(void)
  {
//--- Let us check if the user set a max profit/loss limit
   if(max_loss > 0 || max_profit > 0)
     {
      //--- If true, let us inspect whether we have passed the limit.
      if((PositionGetDouble(POSITION_PROFIT) > max_profit) || (PositionGetDouble(POSITION_PROFIT) < (max_loss * -1)))
        {
         //--- Close the position
         Trade.PositionClose(Symbol());
        }
     }
  }

AIベースのシステムなので、モデルがポジションに不利な市場の動きを予測するかどうかをチェックする関数を作ってみましょう。このようなシグナルは、市場心理の変化をいち早く示唆するものです。

//+------------------------------------------------------------------+
//| If we predict a reversal, let's close our positions              |
//+------------------------------------------------------------------+
void find_reversal(void)
  {
//--- We have a position
   if(((state[1] == 1) && (forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0))) || ((state[2] == 1) && (forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))))
     {
      Trade.PositionClose(Symbol());
     }
  }

次に、有効なエントリシグナルをチェックする関数を定義します。エントリシグナルは、2つの条件を満たした場合に有効とみなされます。1つ目は、より高い時間枠での価格水準の変化によってサポートされていること、2つ目は、私たちのAIモデルがこの高いトレンドに沿った値動きを予測していることです。この2つの条件が満たされた場合、テクニカル指標をチェックし、最終的なレベルを確認します。

//+------------------------------------------------------------------+
//| This function will determine if we have a valid entry            |
//+------------------------------------------------------------------+
void find_entry(void)
  {
//--- First we want to know if the higher timeframes are moving in the same direction we want to go
   double higher_time_frame_trend = iClose(Symbol(),PERIOD_W1,16) - iClose(Symbol(),PERIOD_W1,0);

//--- If price levels appreciated, the difference will be negative
   if(higher_time_frame_trend < 0)
     {
      //--- We may be better off only taking buy opportunities
      //--- Buy opportunities are triggered when the model's prediction is greater than the current price
      if(forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))
        {
         //--- We will use technical indicators to time our entries
         bullish_sentiment();
        }
     }

//--- If price levels depreciated, the difference will be positive
   if(higher_time_frame_trend > 0)
     {
      //--- We may be better off only taking sell opportunities
      //--- Sell opportunities are triggered when the model's prediction is less than the current price
      if(forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0))
        {
         //--- We will use technical indicators to time our entries
         bearish_sentiment();
        }
     }
  }

さて、テクニカル指標を解釈する関数に到達しました。これらの指標を解釈する方法はいろいろありますが、50を中心に考えることにしています。そうすることで、50より大きい値は強気心理を、50より小さい値は弱気心理を示します。出来高指標にはマネーフロー指数(MFI)を、トレンドの強さ指標にはウィリアムズパーセンテージレンジ(WPR)を使用します。

//+------------------------------------------------------------------+
//| This function will interpret our indicators for buy signals      |
//+------------------------------------------------------------------+
void bullish_sentiment(void)
  {
//--- For bullish entries we want strong volume readings from our MFI
//--- And confirmation from our WPR indicator
   wpr_reading.CopyIndicatorBuffer(wpr_handler,0,0,1);
   mfi_reading.CopyIndicatorBuffer(mfi_handler,0,0,1);
   if((wpr_reading[0] > -50) && (mfi_reading[0] > 50))
     {
      //--- Get the ask price
      ask_price = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
      //--- Make sure we have no open positions
      if(PositionsTotal() == 0)
         Trade.Buy(trading_volume,Symbol(),ask_price,(ask_price - sl_width),(ask_price + sl_width),"Custom Deep Neural Network");
      update_state(1);
     }
  }

//+------------------------------------------------------------------+
//| This function will interpret our indicators for sell signals     |
//+------------------------------------------------------------------+
void bearish_sentiment(void)
  {
//--- For bearish entries we want strong volume readings from our MFI
//--- And confirmation from our WPR indicator
   wpr_reading.CopyIndicatorBuffer(wpr_handler,0,0,1);
   mfi_reading.CopyIndicatorBuffer(mfi_handler,0,0,1);
   if((wpr_reading[0] < -50) && (mfi_reading[0] < 50))
     {
      //--- Get the bid price
      bid_price = SymbolInfoDouble(Symbol(),SYMBOL_BID);
      if(PositionsTotal() == 0)
         Trade.Sell(trading_volume,Symbol(),bid_price,(bid_price + sl_width),(bid_price - sl_width),"Custom Deep Neural Network");
      //--- Update the state
      update_state(2);
     }
  }

次に、ONNXモデルから予測を得ることに焦点を当てます。このモデルは、[1,4]という形状の入力を期待し、[1,1]という形状の出力を返すことを覚えておいてください。それに応じて入力と出力を格納するベクトルを定義し、OnnxRun関数を使ってモデルの予測を得ます。

//+------------------------------------------------------------------+
//| This function will fetch forecasts from our model                |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- First we get the input data ready
   vector input_data = {iOpen(_Symbol,PERIOD_CURRENT,0),iHigh(_Symbol,PERIOD_CURRENT,0),iLow(_Symbol,PERIOD_CURRENT,0),iClose(_Symbol,PERIOD_CURRENT,0)};
//--- Now we need to perform inferencing
   if(!OnnxRun(model,ONNX_DATA_TYPE_FLOAT,input_data,forecast))
     {
      Comment("Failed to obtain a forecast from the model: ",GetLastError());
      forecast[0] = 0;
      return;
     }
//--- We succeded!
   Comment("Model forecast: ",forecast[0]);
  }

これで、EAの初期化時に呼び出されるアプリケーションのイベントハンドラを作り始めることができます。この手順では、まずユーザー入力を検証し、次にONNXモデルの入出力形状を定義します。次に、テクニカル指標を設定し、市場データを取得し、最後にシステムの状態を0に設定します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Make sure user inputs are valid
   if(!valid_inputs())
     {
      Comment("Invalid inputs were passed to the application.");
      return(INIT_FAILED);
     }

//--- Create the ONNX model from the buffer
   model = OnnxCreateFromBuffer(ModelBuffer,ONNX_DEFAULT);

//--- Check if we were succesfull
   if(model == INVALID_HANDLE)
     {
      Comment("[ERROR] Failed to create the ONNX model from the buffer: ",GetLastError());
      return(INIT_FAILED);
     }

//--- Set the input shape of the model
   ulong input_shape[] = {1,4};

//--- Check if we were succesfull
   if(!OnnxSetInputShape(model,0,input_shape))
     {
      Comment("[ERROR] Failed to set the ONNX model input shape: ",GetLastError());
      return(INIT_FAILED);
     }

//--- Set the output shape of the model
   ulong output_shape[] = {1,1};

//--- Check if we were succesfull
   if(!OnnxSetOutputShape(model,0,output_shape))
     {
      Comment("[ERROR] Failed to set the ONNX model output shape: ",GetLastError());
      return(INIT_FAILED);
     }

//--- Setup the technical indicators
   wpr_handler = iWPR(Symbol(),PERIOD_CURRENT,wpr_period);
   mfi_handler = iMFI(Symbol(),PERIOD_CURRENT,mfi_period,VOLUME_TICK);

//--- Fetch market data
   minimum_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN);
   trading_volume = minimum_volume * lot_multiple;

//--- Set the system to state 0, indicating we have no open positions
   update_state(0);

//--- Everything went fine
   return(INIT_SUCCEEDED);
  }

このアプリケーションで重要なのは、初期化解除の手順です。このイベントハンドラでは、EAが使用されていないときに、不要になったリソースを解放します。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free the onnx resources
   OnnxRelease(model);

//--- Free the indicator resources
   IndicatorRelease(wpr_handler);
   IndicatorRelease(mfi_handler);

//--- Detach the expert advisor
   ExpertRemove();
  }

最後に、OnTickイベントハンドラを定義する必要があります。取られるアクションはシステムの状態によって異なります。ポジションがない場合（状態0）、モデルから予測を得て、エントリの可能性を特定することを優先します。ポジション（ロングの場合は状態1、ショートの場合は状態2）を持っている場合、焦点をポジションの管理に移します。これには、反転の可能性を監視し、リスクレベル、利益目標、最大利益レベルをチェックすることが含まれます。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Which state is the system in?
   if(state[0] == 1)
     {
      //--- Being in this state means we have no open positions, let's analyse the market to try find one
      model_predict();
      find_entry();
     }

   if((state[1] == 1) || (state[2] == 1))
     {
      //--- Being in this state means we have an position open, if our model forecasts a reversal move we will close
      model_predict();
      find_reversal();
      check_profit_level();
     }
  }
//+------------------------------------------------------------------+

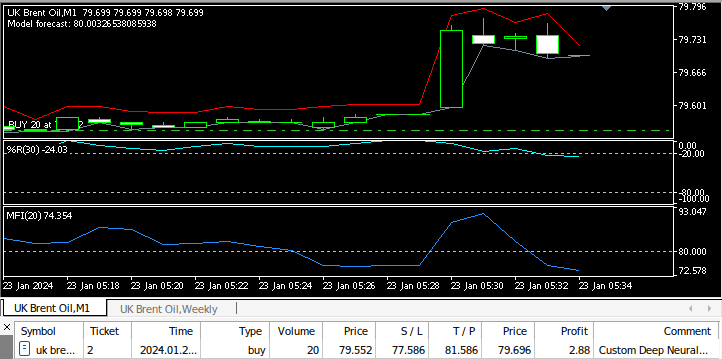
図9：EAのテスト

結論

この記事では、モデルのハイパーパラメータ選択に最適化アルゴリズムを使う方法を簡単に紹介しました。今後の記事では、より堅牢な方法論を採用し、2つの別々のデータセットを活用します。1つはモデルを最適化するためのデータセット、もう1つはデフォルト設定を使用したモデルとのパフォーマンスの相互検証および比較のためのデータセットです。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15413

添付されたファイル |

ZIPをダウンロード

Brent_M1.onnx (1 KB)

Custom_Deep_Neural_Network.mq5 (11.17 KB)

Parameter_Tuning_Deep_Neural_Networks.ipynb (129.93 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

Deus EAの実装：MQL5におけるRSIと移動平均を使った自動売買

この記事では、RSIと移動平均指標に基づいて自動売買をおこなうDeus EAの実装手順を概説します。

データサイエンスと機械学習（第28回）：AIを使ってEURUSDの複数の先物を予測する

多くの人工知能モデルでは単一の将来値を予測することが一般的ですが、この記事では、機械学習モデルを用いて複数の将来値を予測するという強力な手法について掘り下げていきます。このアプローチは「多段階予測」として知られ、明日の終値だけでなく、明後日以降の値も予測することが可能です。多段階予測をマスターすることで、トレーダーやデータサイエンティストはより深い洞察を得ることができ、情報に基づいた意思決定を行うことで予測能力と戦略立案を大幅に強化することができます。

知っておくべきMQL5ウィザードのテクニック（第30回）：機械学習におけるバッチ正規化のスポットライト

バッチ正規化とは、ニューラルネットワークのような機械学習アルゴリズムに投入するデータの前処理です。これは、アルゴリズムが使用する活性化の種類を常に意識しながらおこなわれます。そこで、エキスパートアドバイザー(EA)を使って、そのメリットを享受するためのさまざまなアプローチを探ります。

古典的な戦略をPythonで再構築する（第3回）：高値更新と安値更新の予測

本連載では、古典的な取引戦略を実証的に分析し、AIを用いてそれらの改善が可能かどうかを検証します。本日の議論では、線形判別分析モデルを用いて高値更新と安値更新の予測に挑戦します。