知っておくべきMQL5ウィザードのテクニック（第16回）：固有ベクトルによる主成分分析

はじめに

主成分分析(PCA)とは、データセットの多くの次元の中から「主成分」のみに焦点を当てて「非主成分」の部分を無視することによってデータセットの次元を小さくすることです。おそらく次元削減の最も単純な例は、以下に示すような行列でしょう。

これがデータポイントであった場合、次の1つの値として再表現することができます。

この1つの値は、9から1への次元の削減を意味します。上の図解は行列をその行列式に還元するもので、これは緩やかに次元削減と等価です。

しかし、PCAは、固有値と固有ベクトルについて、少し深いアプローチを取ります。通常、PCAで扱われるデータセットは行列形式であり、行列から求められる主成分は、他の行列ベクトルの中で最も有意であり、行列全体の代表として十分な単一のベクトル列（または行）です。上記の「はじめに」で言及したように、これがPCAと呼ばれているのは、このベクトルだけで行列全体の主成分を保持することができるためです。特異値分解(SVD)やべき乗法などの他の選択肢があるため、このベクトルの特定は必ずしも固有ベクトルや固有値によっておこなわれる必要はありません。

SVDは、行列データセットを3つの別々の行列に分割することによって次元削減を達成することができ、この3つのうちの1つであるΣ行列は、データにおける分散の最も重要な方向を特定します。対角行列としても知られるこの行列には特異値が含まれ、これはあらかじめ特定された各方向（3つの行列のもう1つに記録され、しばしばUと呼ばれる）に沿った分散の大きさを表します。特異値が大きいほど、データのばらつきを説明する上で対応する方向が有意であることを意味します。これにより、最も特異値の高いU列が行列全体の代表として選択されることになり、次元の削減につながります（行列から単一のベクトルへ）。

逆に、べき乗法は、ベクトル推定値を繰り返し精緻化し、支配的な固有ベクトルに収束させます。この固有ベクトルは、データ中の最も大きな変動を持つ方向を捉え、元の行列の次元を削減したものに相当します。

しかし、固有ベクトルと固有値に注目すると、n×nの行列をn個の可能なnサイズのベクトルに縮小することができ、これらのベクトルにはそれぞれ固有値が割り当てられます。この固有値は、次に行列を最もよく表す固有ベクトルの選択を知らせ、やはり値が高いほどデータの変動を説明する上で正の相関が高いことを示します。

では、データセットの次元を下げることに何の意味があるのでしょうか。一言で言えば、私は答えはホワイトノイズ（英語）を管理するためだと感じています。しかし、もっと丁寧な回答は、視覚化を改善するためにということでしょう。高次元のデータは、散布図や典型的なグラフ形式のようなメディアにプロットして表示するのが面倒だからです。寸法（プロット座標）を2つか3つに減らすと、これが解決します。予測時にデータポイントを比較する際の計算コストを削減できることも大きな利点です。

この比較はモデルの訓練時におこなわれるため、モデルの訓練時間や計算能力を節約できます。これは「次元の呪い」につながります。高次元のデータは、訓練中にサンプルでテストすると正確な結果を出す傾向がありますが、交差検証では低次元のデータよりも急速に性能が低下します。次元を下げるすることで、この問題を解決することができます。また、次元を下げることで、データセットのノイズは減少する傾向にあり、理論的にはパフォーマンスが向上するはずです。そして最後に、低次元のデータはストレージスペースを取らないため、特に大規模なモデルを訓練する際に、より効率的に管理することができます。

PCAと固有ベクトル

形式的には、固有ベクトルは方程式で定義されます。

Av =λv

ここで

• A：変換行列
• v：変換されるベクトル
• a、λ：ベクトルに適用されるスケールファクター

固有ベクトルの背後にある中心的な考え方は、サイズn×nの多くの（すべてではない）正方行列Aについて、行列Aをこれらのベクトルのいずれかに適用したときに、結果の積の方向が元のベクトルと同じ方向を維持し、唯一の変化は元のベクトルの値の比例スケールであるようなサイズnのn個のベクトルがそれぞれ存在するということです。このスケールは、上式ではλとして参照され、固有値と呼ぶのが適切です。各固有ベクトルには1つの固有値があります。

すべての行列が必要な数の固有ベクトルを生成するわけではなく、いくつかの行列は変形しています。ただし、生成されたベクトルごとに、元の行列の縮小された次元の候補が存在します。これらのベクトルの中から勝利ベクトルを選択するのは固有値に基づいています。値が大きいほどデータセットの分散をよりよくとらえ、ノイズをあまりとらえないからです。

固有ベクトルを特定するプロセスは、データセットの行列を正規化することから始まり、いくつかのオプション（英語）が利用可能です。この記事では標準得点を使用します。行列データを正規化した後、分散共分散行列等価物を計算します。行列の各要素は任意の2つの要素間の共分散を表し、対角は各要素のそれ自身との共分散を表します。共分散行列を使用する場合、固有ベクトルと固有値を計算する際の計算効率が高くなることに加え、共分散行列から生成されるデータ値は、行列内のデータ点間の線形関係を捉え、行列内の各データ点が他のデータ点とどのように共分散するかを明確に示します。

行列データ型の共分散行列の計算は、MQL5の組み込み関数、この場合はCov()関数で処理されます。共分散行列が得られたら、固有ベクトルと固有値も内蔵関数Eig()で計算できます。固有ベクトルとそれぞれの値が得られたら、固有ベクトル行列を転置し、元の戻り値の行列と掛け合わせます。行列の行は各ポートフォリオの分散加重を表し、したがって選択されるポートフォリオはこれらの加重に依存します。これは、その方向がサンプリングされたデータセット内のデータの最大分散を表しているからです。

楕円の曲線に沿ったxとyの座標をデータセットとし、各データ点をxとyの2次元とすると、最大分散を捉えるという点を強調する簡単な図ができます。この楕円をグラフにプロットすると、下図のようになります。

出典 

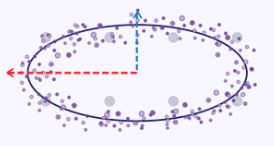
そのため、これらのxとyの次元を1つの（より小さい数の）次元に減らすという問題を課された場合、上のプロット画像からわかるように、楕円はそのy軸よりもx軸に沿って大きく伸びる傾向があるため、x座標値の方が2つのうちでより良い代表となるでしょう。

ただし、一般的には、次元を下げることと情報を保持することの間には、トレードオフとバランスがあります。次元削減には上記のような利点がありますが、その解釈と説明のしやすさには留意すべきです。

MQL5でのコーディング

固有ベクトルを用いたPCAを利用する取引システムは、通常、異なる反復のセット（複数可）からポートフォリオを最適に選択することによっておこなわれます。これを説明するために、冒頭で見た行列を単純にベクトルの構成要素とすることができます。各ベクトルは、3つの異なる配分レジーム下での各資産の1ドル投資に対するリターンを表しています。各ベクトル（ポートフォリオ）の実際の配分の重みが重要になるのは、固有ベクトルが選択され、そのベクトルに沿って採用する資産配分が、将来の投資をおこなうために必要になってからです。

資産がSPY、TLT、PDBCの場合、これらのETFのそれぞれの5年間のリターンに基づく暗示的配分は以下のようになります。

つまり、固有ベクトルを用いたPCAは、過去5年間のパフォーマンスに基づいて、これら3つの選択肢の中から理想的なポートフォリオ（資産配分）を選択するのに役立つということです。上記のステップを再確認すると、最初におこなう必要があるのは、常にデータセットを正規化することです。前述のように、これにはz正規化を使用しており、それを実行するためのソースコードは次のとおりです。

//+------------------------------------------------------------------+
//| Z-Normalization                                                  |
//+------------------------------------------------------------------+
matrix ZNorm(matrix &M)
{  matrix _z;
   _z.Init(M.Rows(), M.Cols());
   _z.Copy(M);
   if(M.Rows() > 0 && M.Cols() > 0)
   {  double _std_min = (M.Max() - M.Min()) / (M.Rows() * M.Cols());
      if(_std_min > 0.0)
      {  double _mean = M.Mean();
         double _std = fmax(_std_min, M.Std());
         for(ulong i = 0; i < M.Rows(); i++)
         {  for(ulong ii = 0; ii < M.Cols(); ii++)
            {  _z[i][ii] = (M[i][ii] - _mean) / _std;
            }
         }
      }
   }
   return(_z);
}

リターン行列を正規化したら、正規化した行列の共分散行列を計算します。MQL5には行列用のデータ型が組み込まれており、これを1行で処理することができます。

   matrix _z = ZNorm(_m);
   matrix _cov_col = _z.Cov(false);

行列内の各データの共分散関係から、固有ベクトルと固有値を求めることができます。これも一行です。

   matrix _e_vectors;
   vector _e_values;
   _cov_col.Eig(_e_vectors, _e_values);

上記の関数からの出力は2つあり、私たちの興味は主に行列として返される固有ベクトルにあります。この行列を転置し、元のリターンの行列と掛け合わせると、私たちが求めているもの、つまり射影行列Pが得られます。これは、可能性のあるポートフォリオごとに行を持つ行列で、各行の列は、生成された3つの固有ベクトルのそれぞれに対する重み付けを表します。例えば、最初の行では、最大の値は最初の列にあります。つまり、このポートフォリオのリターンの分散のほとんどは、第一固有ベクトルに起因しています。この固有ベクトルの固有値を見ると、3つのうちで最も大きいことがわかります。したがって、3つのポートフォリオすべてにおいて、最初のポートフォリオがデータ行列に表れた有意なパターン（または傾向）の大部分を占めていることを意味しています。

私たちのケースでは、各列がポートフォリオを表しているため、列ごとに値を合計すると、すべてのポートフォリオがプラスのリターンをもたらしていました。実際、債券ETF PDBCを保有した場合のリターンは、配分に関係なくマイナスのみです。つまり、ヘッジされた、あるいは分散された、あるいは良いベータのリターンを「永続」させたいのであれば、ポートフォリオ1に固執する必要があるということです。繰り返しになりますが、リターンデータ行列から得られる全体的なテーマは、株式とコモディティのプラスリターンと債券のマイナスリターンです。そのため、固有ベクトルを用いたPCAでは、ポートフォリオ1のように、この傾向が続く可能性が最も高いポートフォリオをフィルタリングすることができますし、投影行列では3行目の最大値が3列目にあり、3番目の固有ベクトルが最小値であったため、逆にポートフォリオ3をフィルタリングすることもできます。

注目すべきは、このポートフォリオは最高のリターンを持っておらず、このプロセスはそれ自体を選択するものではないということです。現状維持に重みを置いていることを示すだけです。検査で簡単に選択できるのに、不必要に複雑に聞こえますが、返される行列や分析される行列が大きくなり、行や列が増えると（固有ベクトルを含むPCAは正方行列を必要とする）、このプロセスは実を結び始めます。

シグナルクラスでPCAを紹介するためには、デフォルトでは1つの時間枠で1つの銘柄しかテストできないという制約があります。つまり、ポートフォリオの選択に関して上で述べた概念は、そのままでは適用できないということです。これらの制約を回避する方法はあり、将来的には別の記事で取り上げることができるかもしれませんが、今はこれらの制約の中で仕事をすることにしましょう。

ここでおこなうのは、日足時間枠の1つの銘柄について、曜日ごとの価格変動を分析することです。1週間の取引日は5日なので、行列は5列となり、PCA固有ベクトル分析に必要な5行を得るために、Open、High、Low、Close、Typicalの5つの異なる価格タイプを考慮します。固有ベクトルと固有値の決定は、すでに述べたステップに従います。

影響行列を入手する際も同様で、それが手に入れば、最も分散をとらえている取引曜日と適用価格タイプを簡単に読み取ることができます。以下のスクリプトのコードに従います。

   matrix _t = _e_vectors.Transpose();
   matrix _p = _m * _t;
   //Print(" projection: \n", _p);
   vector _max_row = _p.Max(0);
   vector _max_col = _p.Max(1);
   double _days[];
   _max_row.Swap(_days);
   PrintFormat(" best trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMaximum(_days)+1)));
   ENUM_APPLIED_PRICE _price[__SIZE];
   _price[0] = PRICE_OPEN;
   _price[1] = PRICE_WEIGHTED;
   _price[2] = PRICE_MEDIAN;
   _price[3] = PRICE_CLOSE;
   _price[4] = PRICE_TYPICAL;
   double _prices[];
   _max_col.Swap(_prices);
   PrintFormat(" best applied price is: %s", EnumToString(_price[ArrayMaximum(_prices)]));
   PrintFormat(" worst trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMinimum(_days)+1)));
   PrintFormat(" worst applied price is: %s", EnumToString(_price[ArrayMinimum(_prices)]));

ログ出力は、以下の「戦略テストと結果」に示されています。

上記のログから、スクリプトが添付されたチャートの銘柄（スクリプトはEURJPYに添付）のプライスアクションの変動の大部分は、木曜日と終値シリーズが原因であることがわかります。これは何を意味するのでしょうか。EURJPYの全体的なトレンドとプライスアクションが興味深く、今後も同じようなプレーをしたいのであれば、木曜日に取引を集中させ、終値シリーズを使用する方が良いということです。仮にEURJPYがポートフォリオのセットポジションの一部であり、今後EURJPYへのエクスポージャーを削減するとしたら、ポジション行列はどのように役立つでしょうか。「最悪の」取引日と価格系列は、EURJPYのポジションを決済するタイミングと方法を決定する際に使用できます。

そこで、ポジション行列では、取引日と価格系列を推奨しているので、これらを考慮した以下のシンプルなシグナルクラスを使用してみましょう。

   int _buffer_size = CopyRates(Symbol(), Period(), __start, __stop, _rates);
   PrintFormat(__FUNCSIG__+" buffered: %i",_buffer_size);
   if(_buffer_size >= 1)
   {  for(int i = 1; i < _buffer_size - 1; i++)
      {  TimeToStruct(_rates[i].time,_datetime);
         int _iii = int(_datetime.day_of_week)-1;
         if(_datetime.day_of_week == SUNDAY || _datetime.day_of_week == SATURDAY)
         {  _iii = 0;
         }
         for(int ii = 0; ii < __SIZE; ii++)
         {  
                ...

                ...
         }
      }
   }

戦略テストと結果

MQL5ウィザードで組み立てたEAでバックテストをおこなうには、まず、テストする銘柄のチャートと時間枠でスクリプトを実行する必要があります。この例では、4時間枠のEURUSDを使用しています。チャート上でスクリプトを実行すると、4時間足のEURUSDの「理想的な」または分散を決定するパラメータとして、金曜日と加重価格が得られます。これは以下のログに示されています。

2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best trade day is: FRIDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best applied price is: PRICE_WEIGHTED
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst trade day is: TUESDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst applied price is: PRICE_OPEN

このスクリプトには、分析対象期間を決定する2つの入力パラメータ、すなわち開始時刻と停止時刻もあります。どちらもdatetime変数です。これらを2022.01.01と2023.01.01に設定し、まずこの期間でEAをテストし、次に2023.01.01から2024.01.01の期間で同じ設定で交差検証をおこないます。スクリプトは、分散を決定する変数として、金曜日と加重価格を推奨しています。シグナルクラスの開発でこの情報をどのように活用すればよいのでしょうか。いつものように、検討できるオプションは多数ありますが、ここでは単純な価格と移動平均のクロスオーバー指標に注目します。推奨される適用価格の移動平均を使用し、また推奨される平日のみに取引をおこなうことで、スクリプトから提示された相互検証を試みます。したがって、ExpertSignalクラスのコードは非常にシンプルなものになります。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::LongCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
   m_time.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) > m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) < m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::ShortCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) < m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) > m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}

いつものように、利食いや損切りに目標株価は使用せず、指値注文でエントリします。これは、EAがいったんポジションを建てると、反転したときだけ決済されることを意味します。間違いなくハイリスクなアプローチですが、私たちの目的にはこれで十分です。最初の期間でバックテストを実施すると、次のようなレポートとエクイティ曲線が得られます。

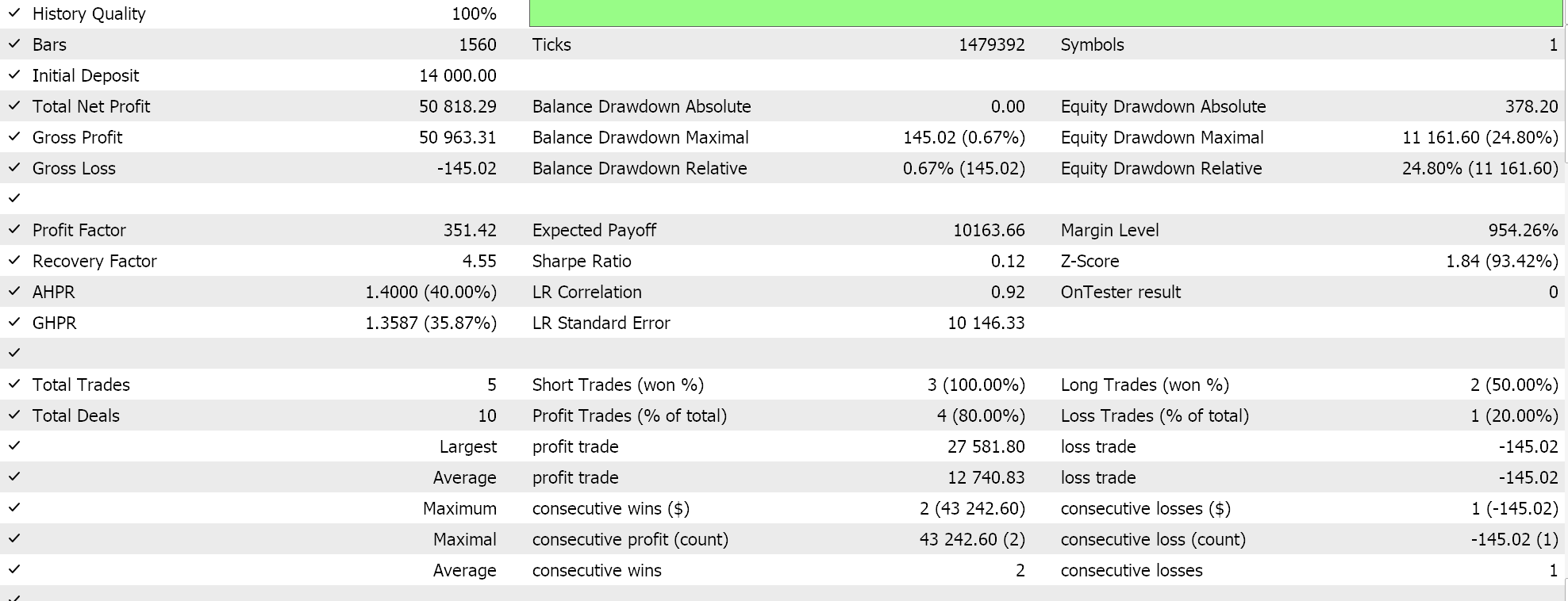
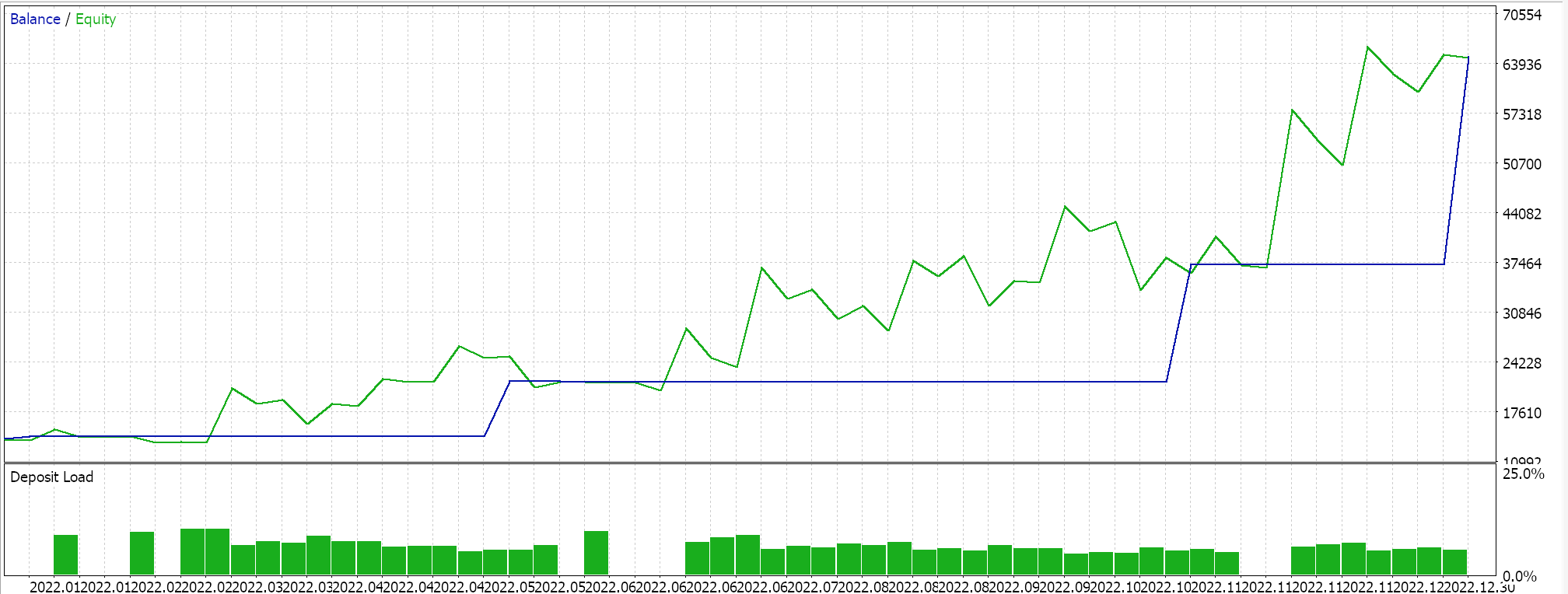
上記の結果は2022.01.01から2023.01.01までのものです。スクリプトの分析期間を超えて、2022.01.01から2024.01.01まで、より長い期間にわたって同じ設定でテストしてみると、結果は次のようになります。

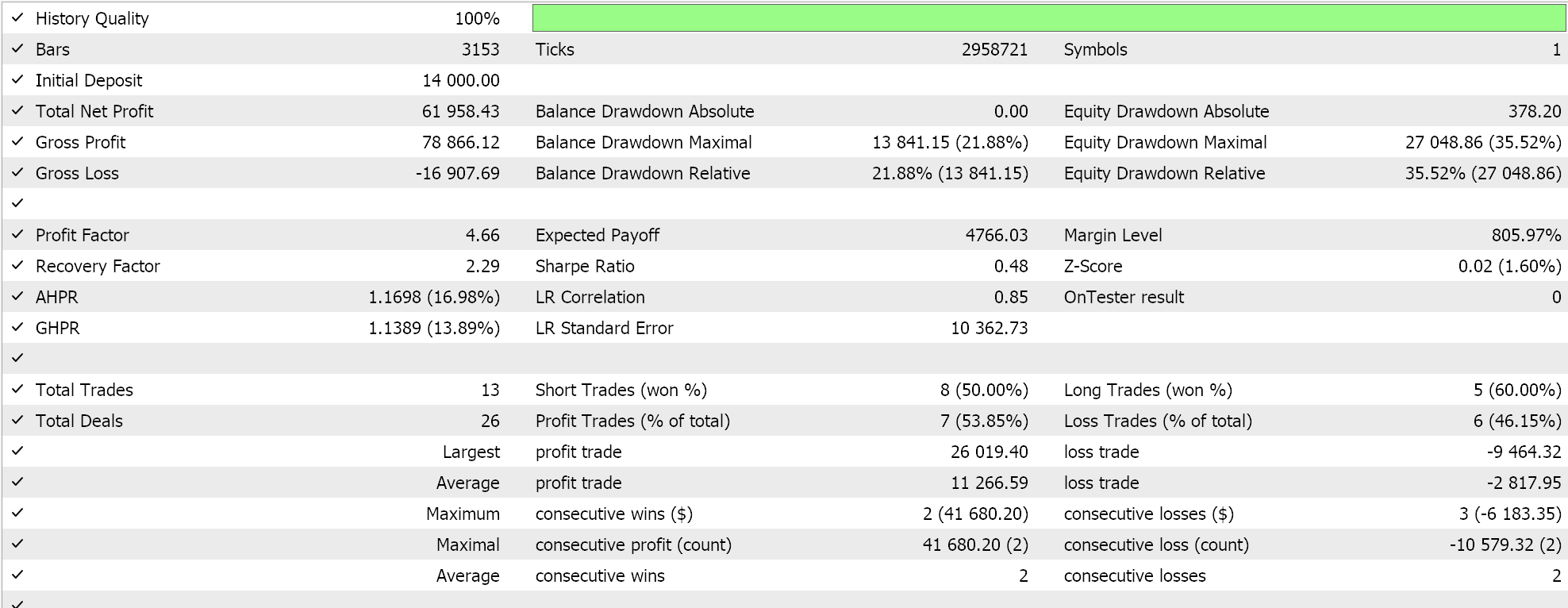
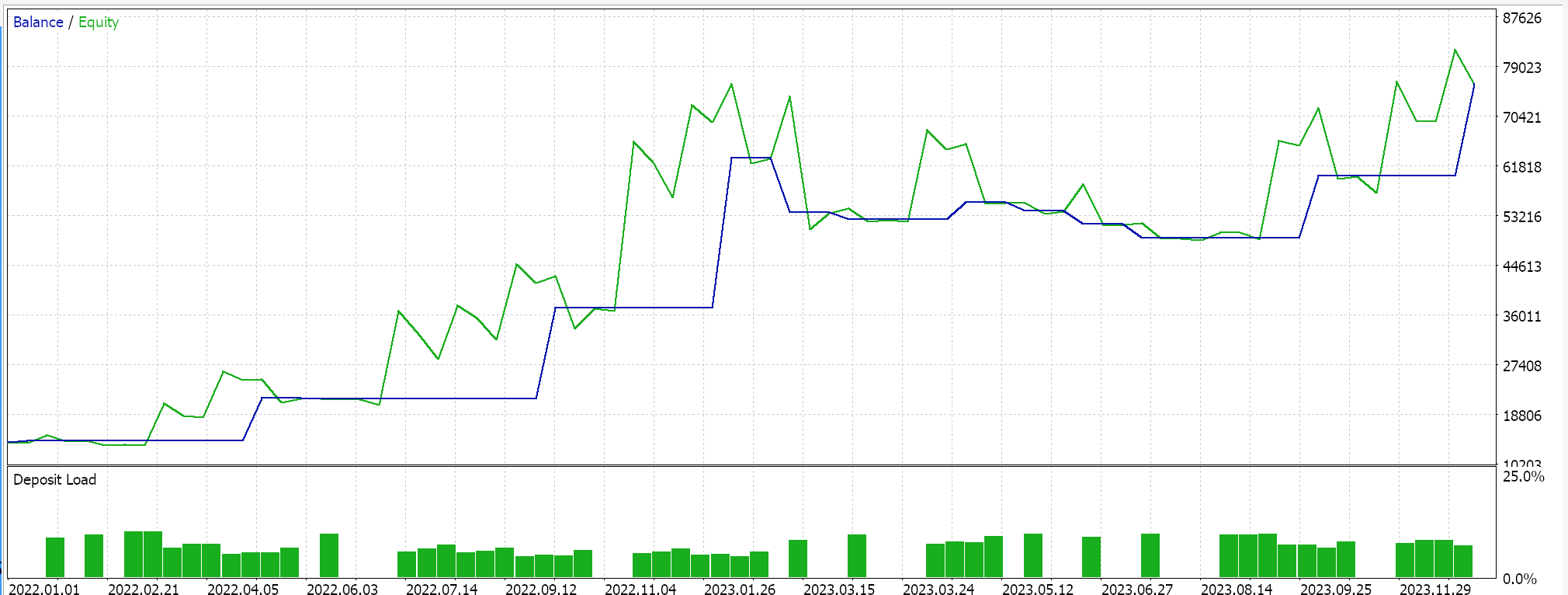
私たちのEAシグナルは少し制限的で、あまり多くの取引はおこなわれていません。これは十分なテストとは言えないと主張する人もいるでしょう。とはいえ、数年というテスト期間は、ライブ口座での運用を考える上では信頼性に欠けます。コントロールとして、上記の交差検証の他に、同じEAの設定で曜日を問わず取引しながら、異なる適用価格でテストを実行することもできます。これは以下のような結果を生みます。

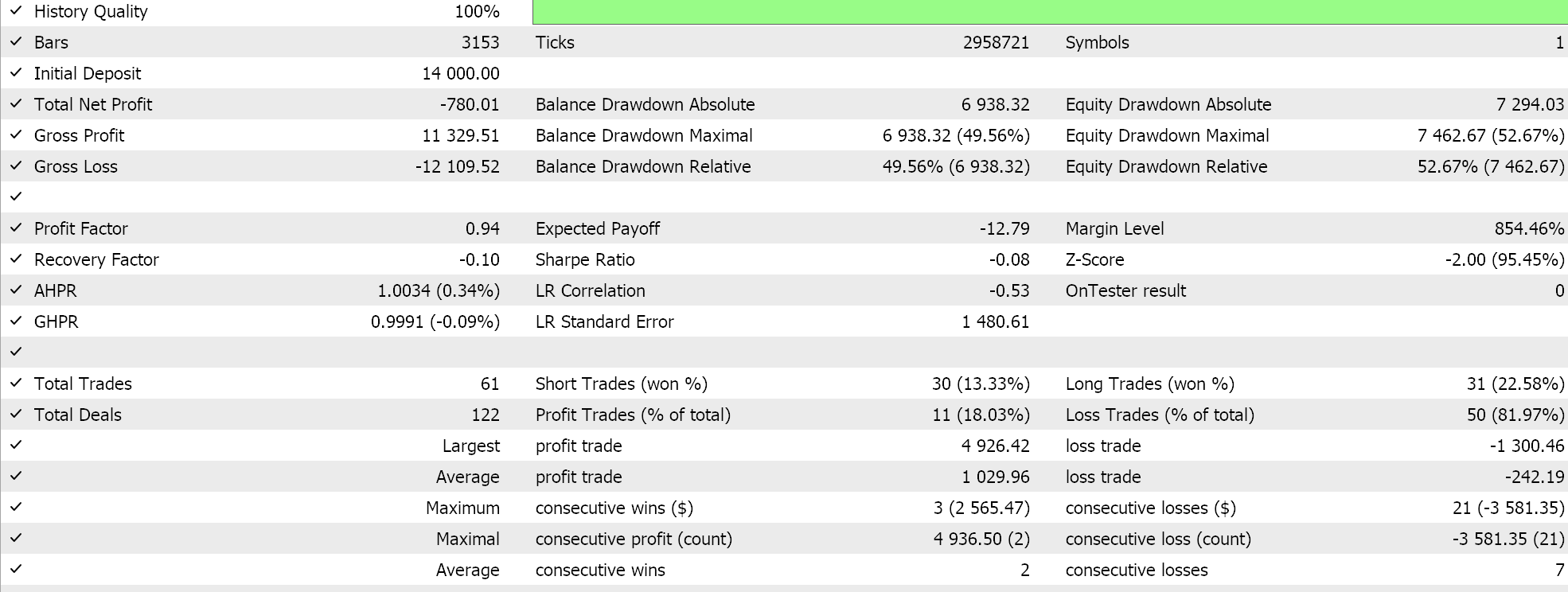
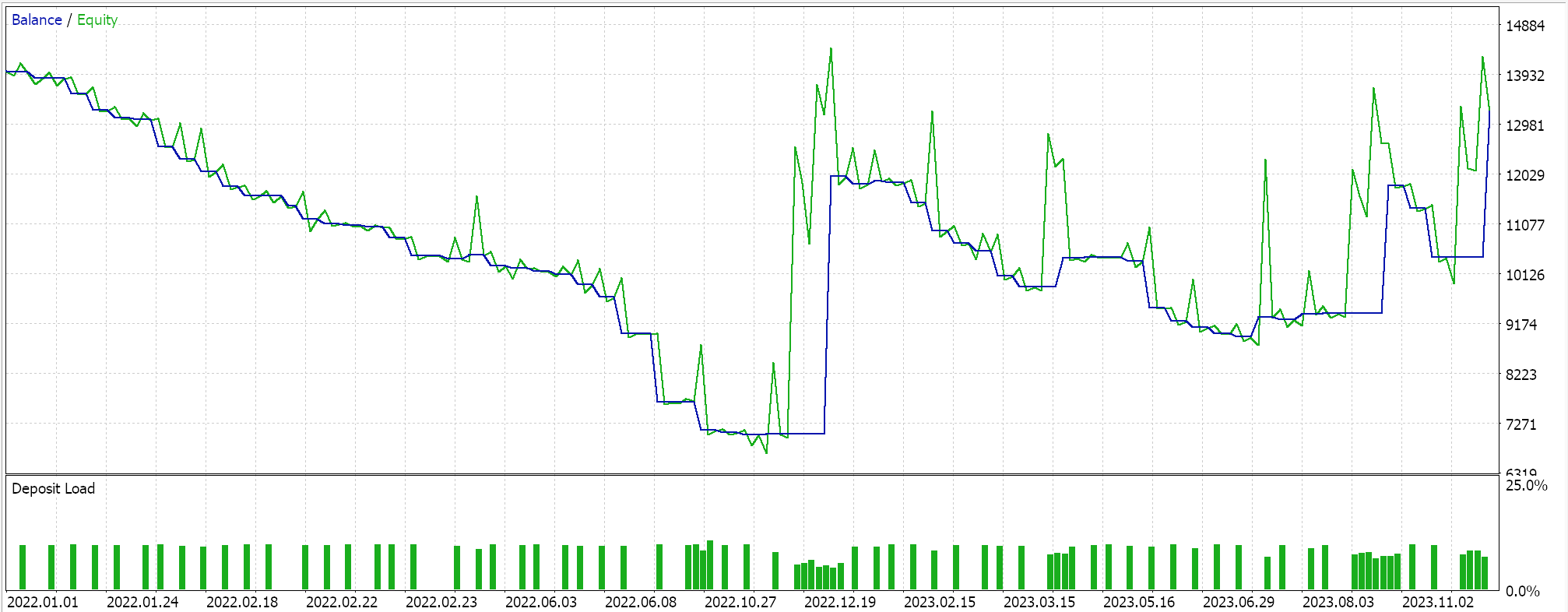
PCAスクリプトの推奨範囲を超えると、全体的なパフォーマンスは明らかに低下します。なぜ、分散を決定するパラメータの範囲内でのみ取引すると、制約のない設定よりも良い結果が得られるのでしょうか。これは関連性のある質問だと思います。調査対象のデータセットの全体的なトレンドはウィップソーになる可能性があるため、分散に影響を与えることが必ずしも収益性の向上を意味するわけではないからです。このため、最も分散を決定する設定を選択するのは、調査対象のデータセットにおける基礎的かつ全体的な傾向が、トレーダーの全体的な目的と一致している場合に限られるべきです。

EURUSDの価格チャートを見ると、2022.01.01から2023.01.01のPCA分析期間において、EURUSDは10月に一時的に反転するまでは、ほとんどが下降トレンドであったことがわかります。しかし、交差検証期間である2023年には、2022年のような大きなトレンドは生まれず、大きく揺れ動きました。このことは、主要なトレンド期間にわたって分析をおこなうことで、トレンドを設定する分散パラメータをよりよく捉えることができ、2023年に明らかなように、ウィップソー状況においても有用であることを示唆していると考えられます。

結論

まとめると、PCAは本質的に、データセットの根本的な傾向を決定する最も重要な次元（またはデータセットの成分）を特定することによって、データセットの次元を削減しようとする分析ツールであることがわかりました。データの次元を削減するための利用可能なツールは数多くあります。PCAは表面的には興味深く思えないかもしれませんが、それが常に調査されたデータセットの根本的な傾向に基づいていることを考えると、慎重な分析と解釈が必要です。

テスト中の例では、調査した銘柄の基調トレンドは弱気であり、これに基づいて交差検証をおこなったところ、サンプル外の取引の大半はショートでした。仮に、検討中の銘柄の強気相場を調査していたとすると、推奨されるPCA設定に基づいて採用される取引戦略は、強気環境を利用する必要があります。逆に、弱気相場と強気相場は正反対であるため、弱気相場を利用するのであれば、最も分散を説明しにくい設定を選択するのが理にかなっています。また、PCAでは、重み付けと呼ばれる固有値を持つ2つ以上の設定の組が得られ、それらの重み付けが十分な閾値以上であれば、複数の設定を採用できることになります。本稿ではこの点については触れていませんが、ソースコードが以下に添付されているので、この点についてはご自分でお調べください。ウィザードの初心者は、EAを組み立てるためのMQL5ウィザードでのこのコードの使い方をこちらでご覧になれます。

しかし、分析スクリプトとEAをより多くのPCA設定に対応させるために取ることができるアプローチの1つは、例えば、まず固有値がすべて正で0.0から1.0の範囲になるように正規化することです。これが完了すると、各解析から選ぶ固有ベクトルの選択閾値を定義することができます。たとえば、3×3の行列をPCA分析した結果、最初に2.94、1.92、0.14という値が得られた場合、これらの値を0～1の範囲に正規化し、0.588, 0.384, & 0.028とします。正規化された値では、0.3のような閾値ベンチマークによって、複数の分析にわたって公平に固有ベクトルを選択することができます。異なるデータセット、異なる行列サイズで分析を繰り返しても、同様の方法で固有ベクトルを選択することができます。スクリプトの場合、これは固有値を繰り返し処理し、一致した値ごとに2つのクロスプロパティを出力リストまたは配列に追加することを意味します。この配列は、データセット行列のxプロパティとyプロパティの両方を記録する構造体です。EAでは、スケーラビリティのために、フィルタプロパティをカンマで区切られた文字列値として入力する必要があります。そのためには、文字列を解析してプロパティを抽出し、EAが読み取れる標準フォーマットにする必要があります。